力扣 279. 完全平方数
🔗 https://leetcode.cn/problems/perfect-squares
题目
- 给你一个整数
n,返回 和为n的完全平方数的最少数量 - 完全平方数可以拆解为两个相同数的乘积
思路
- dp 公式,就是从看用哪个完全平方数 1 2 4 9…… 到当前 sum 的数量最少
代码
class Solution {
public:int numSquares(int n) {vector<int> dp(n+1);dp[0] = 0;dp[1] = 1;for (int i = 2; i <= n; i++) {dp[i] = dp[i-1] + 1;for (int j = 2; j * j <= i; j++) {dp[i] = min(dp[i], dp[i - j*j] + 1);}}return dp[n];}
};
相关文章:

力扣 279. 完全平方数
🔗 https://leetcode.cn/problems/perfect-squares 题目 给你一个整数 n ,返回 和为 n 的完全平方数的最少数量完全平方数可以拆解为两个相同数的乘积 思路 dp 公式,就是从看用哪个完全平方数 1 2 4 9…… 到当前 sum 的数量最少 代码 …...

鸿蒙生态潮起:开发者的逐浪之旅
鸿蒙生态潮起:开发者的逐浪之旅 在全球科技的澎湃浪潮中,鸿蒙生态宛如一座正在崛起的新大陆,熠熠生辉,吸引着无数开发者扬帆起航,探寻其中蕴藏的无限机遇,也直面诸多挑战。 鸿蒙生态的机遇,首先…...

Diskgenius系统迁移之后无法使用USB启动
前言 本文用于记录系统迁移中遇到的问题及解决方法,如有不对请指出,谢谢! 现象 使用DiskGenius进行系统迁移后,使用USB启动失败,反复在品牌logo和黑屏之间切换,期间还会在左上角显示”reset system“报错…...

Kafka 可靠性探究—副本刨析
Kafka 的多副本机制提升了数据容灾能力。 副本通常分为数据副本与服务副本。数据副本是指在不同的节点上持久化同一份数据;服务副本指多个节点提供同样的服务,每个节点都有能力接收来自外部的请求并进行相应的处理。 1 副本刨析 1.1 相关概念 AR&…...

我的博文天地测试报告
我的博文天地测试报告 文章目录 我的博文天地测试报告 一.项目背景 二.项目功能 2.1 功能介绍 三.测试分类 3.1 功能测试 3.1.1 测试用例 3.1.2 实际执行测试的部分操作步骤/结果的截图 3.2 自动化测试 3.3 性能测试 3.1.2 用户登录 jmeter性能测试结果 性能测试遇到的困难 …...

EtherCAT主站IGH-- 35 -- IGH之pdo_list.h/c文件解析
EtherCAT主站IGH-- 35 -- IGH之pdo_list.h/c文件解析 0 预览一 该文件功能`pdo_list.c` 文件功能函数预览二 函数功能介绍`pdo_list.c` 中主要函数的作用1. `ec_pdo_list_init`2. `ec_pdo_list_clear`3. `ec_pdo_list_clear_pdos`4. `ec_pdo_list_total_size`5. `ec_pdo_list_a…...

嵌入式开发神器:Buildroot的介绍和使用方法
目录 引言**Buildroot 能做什么?****1. 生成交叉编译工具链(Toolchain)****2. 生成嵌入式 Linux 根文件系统(RootFS)****3. 编译 Linux 内核和设备树文件****4. 编译 Bootloader(U-Boot)****5. …...
--边缘计算应用开发详解)
JavaScript系列(61)--边缘计算应用开发详解
JavaScript边缘计算应用开发详解 🌐 今天,让我们深入探讨JavaScript的边缘计算应用开发。边缘计算是一种将计算和数据存储分布到更靠近数据源的位置的架构模式,它能够提供更低的延迟和更好的实时性能。 边缘计算基础架构 🌟 &am…...

【LeetCode】day15 142.环形链表II
142. 环形链表 II - 力扣(LeetCode) 题目描述 给定一个链表的头节点 head ,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。 如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则…...

代理对象与目标对象
1. 定义:代理对象和目标对象 1.1 目标对象(Target Object) 目标对象是指 被增强的原始对象,即需要通过 AOP 切面(Aspect)增强功能的业务对象(原始类)。增强逻辑(Advice…...

【Kubernetes Pod间通信-第3篇】Kubernetes中Pod与ClusterIP服务之间的通信
引言 我们之前了解了在不同场景下,Kubernetes中Pod之间的通信是如何路由的。 【Kubernetes Pod间通信-第1篇】在单个子网中使用underlay网络实现Pod到Pod的通信【Kubernetes Pod间通信-第2篇】使用BGP实现Pod到Pod的通信现在,我们来看看在集群中,Pod与服务之间的通信是如何…...

DNN(深度神经网络)近似 Lyapunov 函数
import torch import torch.nn as nn import torch.optim as optim import matplotlib.pyplot as plt # from torchviz import make_dot import torchviz# 1. Lyapunov 函数近似器(MLP 结构) class LyapunovNet(nn.Module):def __init__(self, input_dim…...

128陷阱
首先我们了解一下关于包装器类型 java是面向对象的语言,但基本类型并不是面向对象的,从而出现了包装器类型,并且包装器添加了更多的属性和方法。如我们在使用集合类型Collection的时候就一定要使用包装类型而非基本类型,它相当于将…...

PromptSource和LangChain哪个更好
目录 1. 设计目标与定位 PromptSource LangChain 2. 功能对比 3. 优缺点分析 PromptSource LangChain 4. 如何选择? 5. 总结 PromptSource 和 LangChain 是两个在自然语言处理(NLP)领域非常有用的工具,但它们的设计目标和…...

构成正方形的数量:算法深度剖析与实践
目录 引言算法核心概念 定义正方形的构成条件数据结构与输入形式算法数学原理 几何关系的数学表达坐标运算与判定逻辑Python 实现 代码展示代码解析Python 实现的优势与局限C 语言实现 代码展示代码解析C 语言实现的性能特点性能分析与优化 性能分析 时间复杂度空间复杂度优化思…...

Redis持久化-秒杀系统设计
在构建高性能、高可用的系统时,Redis 作为缓存和消息队列的角色越来越重要。在一些场景下,我们还需要将 Redis 的数据进行持久化,以确保数据的安全性和恢复能力。除此之外,秒杀系统也越来越成为电商、抢购等平台的核心功能之一。本…...
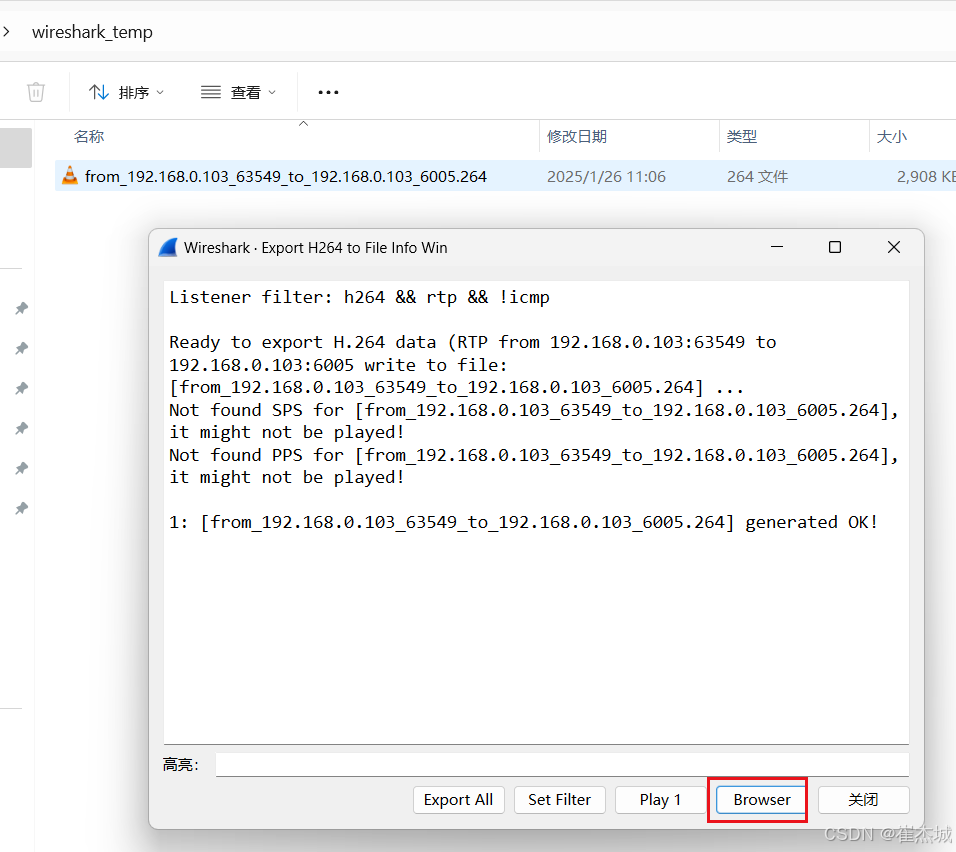
音视频入门基础:RTP专题(8)——使用Wireshark分析RTP
一、引言 通过Wireshark可以抓取RTP数据包,该软件可以从Wireshark Go Deep 下载。 二、通过Wireshark抓取RTP数据包 首先通过FFmpeg将一个媒体文件转推RTP,生成RTP流: ffmpeg -re -stream_loop -1 -i input.mp4 -vcodec copy -an -f rtp …...

OpenAI 实战进阶教程 - 第六节: OpenAI 与爬虫集成实现任务自动化
爬虫与 OpenAI 模型结合,不仅能高效地抓取并分析海量数据,还能通过 NLP 技术生成洞察、摘要,极大提高业务效率。以下是一些实际工作中具有较高价值的应用案例: 1. 电商价格监控与智能分析 应用场景: 电商企业需要监控…...

SpringUI Web高端动态交互元件库
Axure Web高端动态交互元件库是一个专为Web设计与开发领域设计的高质量资源集合,旨在加速原型设计和开发流程。以下是关于这个元件库的详细介绍: 一、概述 Axure Web高端动态交互元件库是一个集成了多种预制、高质量交互组件的工具集合。这些组件经过精…...

解密企业安全密码:密钥管理服务如何重塑数据保护?
在数字化时代,数据是企业最宝贵的资产之一。然而,随着网络威胁的不断升级和数据泄露事件的频繁发生,如何保护企业数据的安全已成为每个组织面临的紧迫问题。传统的安全措施往往无法应对复杂的威胁环境,密钥管理服务作为企业信息安…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...

「全栈技术解析」推客小程序系统开发:从架构设计到裂变增长的完整解决方案
在移动互联网营销竞争白热化的当下,推客小程序系统凭借其裂变传播、精准营销等特性,成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径,助力开发者打造具有市场竞争力的营销工具。 一、系统核心功能架构&…...

c# 局部函数 定义、功能与示例
C# 局部函数:定义、功能与示例 1. 定义与功能 局部函数(Local Function)是嵌套在另一个方法内部的私有方法,仅在包含它的方法内可见。 • 作用:封装仅用于当前方法的逻辑,避免污染类作用域,提升…...
