组合总和II(力扣40)
这道题的难点就在于题目所给的集合中有重复的数字,我们需要进行去重操作。首先明确去重指的是去重哪一部分。注意并不是对递归的集合去重,而是对当前集合的遍历进行去重。这么说可能有点抽象,举个例子:假设集合为1,1,2,3,4,我们第一次选1,递归集合时,我们仍可以选择第二个1。但是在第一次选第二个1时,在往下选,就会出现很多与第一次选第一个1时相同的组合。所以在每一层递归函数的for循环中我们需要进行去重。不过,我们需要判断这个重复出现的数字是在当前这层递归的for循环中还是在下一层递归的for循环中。于是,我们创建了一个数组,标识这些集合中的数字是否被使用过,如果被使用过,说明是在上一层递归中被使用,如果没有被使用,说明是在当前这一层递归的for循环中。大家可以结合我下面的代码及详细注释理解。
代码及详细注释如下:
class Solution {
public:vector<int> path;vector<vector<int>> result;void backtracking(vector<int>& candidates,int target,int sum,int start,vector<int>& used){//剪枝if(sum > target){return;}//终止条件if(sum == target){result.push_back(path);return;}for(int i = start;i < candidates.size();i++){//去重if(i > 0 && candidates[i] == candidates[i - 1] && used[i - 1] == 0){continue;}path.push_back(candidates[i]);sum += candidates[i];used[i] = 1;backtracking(candidates,target,sum,i + 1,used);//回溯path.pop_back();sum -= candidates[i];used[i] = 0;}return;}vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {//创建一个数组,该数组下标对应集合中元素的下标,表示集合中各个下标对应的数字有没有使用过vector<int> used(candidates.size(),0);sort(candidates.begin(),candidates.end());backtracking(candidates,target,0,0,used);return result;}
};相关文章:
)
组合总和II(力扣40)
这道题的难点就在于题目所给的集合中有重复的数字,我们需要进行去重操作。首先明确去重指的是去重哪一部分。注意并不是对递归的集合去重,而是对当前集合的遍历进行去重。这么说可能有点抽象,举个例子:假设集合为1,1,2,3,4&#x…...

基于HTML生成网页有什么优势
在互联网时代,网页是人们获取信息、交流互动的重要窗口,而基于HTML生成网页,是搭建网络大厦的关键。HTML语法简洁直观,标签和属性语义明确,新手也能迅速上手,创建包含基础元素的网页,极大降低了…...

php 接入扣子的 token获取
本身逻辑只是个api,但是官方不提供php的sdk 扎心了老铁,这下php 狗都不用了,主要麻烦的是如何获取access_token,代码如下 protected function get_jwt(): string{$header [alg > RS256,typ > JWT,kid > $this->kid];…...
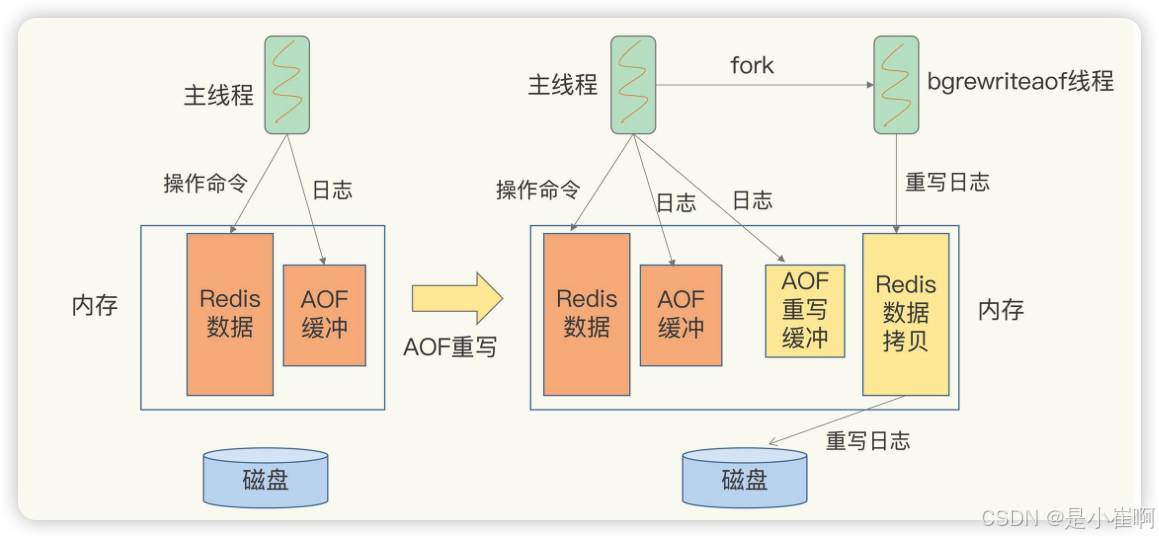
Redis02 - 持久化
Redis持久化 文章目录 Redis持久化一:持久化简介1:Redis为什么要进行持久化2:Redis持久化的方式 二:RDB持久化介绍1:手动触发RDB2:自动触发RDB3:redis.conf中进行RDB的配置4:RDB优缺…...
【力扣】240.搜索二维矩阵 II
题目 我的代码 class Solution { public:bool searchMatrix(vector<vector<int>>& matrix, int target) {for(int i0;i<matrix.size();i){for(int j0;j<matrix[0].size();j){if(targetmatrix[i][j]){return true;}else if(target<matrix[i][j]){brea…...
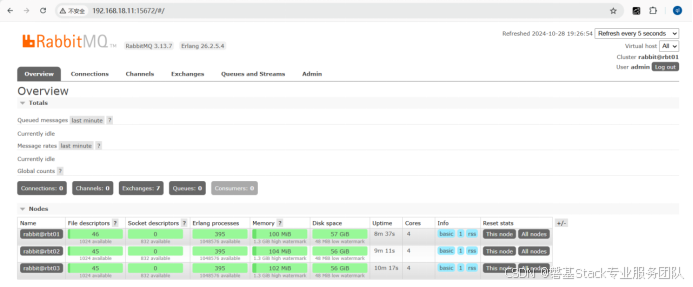
RabbitMQ 从入门到精通:从工作模式到集群部署实战(二)
接上篇:《RabbitMQ 从入门到精通:从工作模式到集群部署实战(一)》 链接 文章目录 4.安装RabbitMQ Messaging Topology Operator 裸金属环境部署RabbitMQ部署单实例部署集群 4.安装RabbitMQ Messaging Topology Operator 使用 cer…...

编程AI深度实战:大模型哪个好? Mistral vs Qwen vs Deepseek vs Llama
随着开源 LLM 的发展,越来越多的模型变得专业化,“代码”LLM 变得非常流行。这些 LLM 旨在比其 “常识” 对应物更小,但旨在超越更大的通用模型的编码性能。 这些模型以极低的成本提供大型模型的功能,进一步使本地 LLM 空间民主化…...

11.kafka开启jmx
方式一: 1.进入/opt/kafka_2.13-3.3.2/bin目录 命令: cd /opt/kafka_2.13-3.3.2/bin [root@rhel77 ~]# cd /opt/kafka_2.13-3.3.2/bin [root@rhel77 bin]# pwd /opt/kafka_2.13-3.3.2/bin [root@rhel77 bin]# 2.备份kafka-run-class.sh 命令: cp kafka-run-class.sh …...

基于钉钉API的连接器实现:企业数据集成与自动化管理
文章目录 概要背景与需求钉钉API概述连接器实现小结 概要 在当今数字化时代,企业面临着海量数据的管理与整合挑战。钉钉作为国内广泛使用的办公协作平台,提供了丰富的API接口,支持企业进行数据集成与自动化管理。本文将介绍如何通过钉钉API实…...

JAVA 二维列表的基础操作与异常
在Java中创建二维 ArrayList(即嵌套列表)的方法有多种,下面我将详细介绍常用的几种方式,并分析它们的区别和适用场景。 1. 使用嵌套 ArrayList 创建二维列表 方法一:直接嵌套 ArrayList 这是最常用的方法,…...

将仓库A分支同步到仓库B分支,并且同步commit提交
一、 问题 有一仓库A 和 一仓库B, 需要将仓库A分支a1所有提交同步推送到仓库B分支b1上 二、 解决 2.1、 首先需要仓库A、仓库B的权限, 2.2、将仓库A clone到本地, 进入A目录,并且切换到a1分支 cd A ## A 为A仓库clone到本地代…...

使用java代码操作rabbitMQ收发消息
SpringAMQP 将来我们开发业务功能的时候,肯定不会在控制台收发消息,而是应该基于编程的方式。由于RabbitMQ采用了AMQP协议,因此它具备跨语言的特性。任何语言只要遵循AMQP协议收发消息,都可以与RabbitMQ交互。并且RabbitMQ官方也…...

mysql8安装时提示-缺少Microsoft Visual C++ 2019 x64 redistributable
MySQL8.0安装包mysql-8.0.1-winx64进行安装,提示:This application requires Visual Studio 2019 x64Redistributable, Please install the Redistributable then runthis installer again。出现这个错误是因为我们电脑缺少Microsoft Visual C 这个程序&…...

WindowsServer搭建内网Gitea【中文更方便使用】
特点: 轻量级:占用系统资源少,对服务器硬件要求较低,适合小型企业或团队使用。部署和维护相对简单,即使没有专业的运维人员也能轻松搭建。 功能齐全:具备基本的代码托管功能,如仓库管理、分支管…...

leetcode 907. 子数组的最小值之和
题目如下 数据范围 观察数据范围理论上平方复杂度的算法计算次数逼近1e9还不至于超时,但是由于有mod 1e9导致超时。所以本题不能靠暴力枚举来解决。 所以我们可以思考如何在枚举上面减少计算次数:第一种枚举法:最外层i控制子数组的左边界&…...

WordPress自定义.js文件排序实现方法
在WordPress中,要将插件引用的.js文件放到所有.js文件之后加载,可以通过以下方法实现: 方法一:调整wp_enqueue_script的加载顺序 在插件的主文件中,使用wp_enqueue_script函数加载.js文件时,将$in_footer…...

摄像头模块烟火检测
工作原理 基于图像处理技术:分析视频图像中像素的颜色、纹理、形状等特征。火焰通常具有独特的颜色特征,如红色、橙色等,且边缘呈现不规则形状,还会有闪烁、跳动等动态特征;烟雾则表现为模糊、无固定形状,…...

【拼十字——树状数组】
题目 暴力代码 30% #include <bits/stdc.h> using namespace std; using ll long long; const int N 1e5 10; const int mod 1e9 7; int n; int l[N], w[N], c[N]; int main() {cin >> n;ll ans 0;for (int i 1; i < n; i){cin >> l[i] >> …...

脚手架开发【实战教程】prompts + fs-extra
创建项目 新建文件夹 mycli_demo 在文件夹 mycli_demo 内新建文件 package.json {"name": "mycli_demo","version": "1.0.0","bin": {"mycli": "index.js"},"author": "","l…...

Fiddler Classic(HTTP流量代理+半汉化)
目录 一、关于Fiddler (一) Fiddler Classic (二) Fiddler Everywhere (三) Fiddler Everywhere Reporter (四) FiddlerCore (五) 总结 二、 软件安全性 1. 软件安装包 2. 软件汉化dll 三、安装与半汉化 1. 正常打开安装包点击下一步安装即可,安装路径自…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...

NPOI Excel用OLE对象的形式插入文件附件以及插入图片
static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...
