LeetCode 128: 最长连续序列
LeetCode 128: 最长连续序列
题目:
给定一个未排序的整数数组 nums ,找出数字连续的最长序列(不要求序列元素在原数组中连续)的长度。
请你设计并实现时间复杂度为 O(n) 的算法解决此问题。
示例 1:
输入:nums = [100,4,200,1,3,2]
输出:4
解释:最长数字连续序列是 [1, 2, 3, 4]。它的长度为 4。
示例 2:
输入:nums = [0,3,7,2,5,8,4,6,0,1]
输出:9
提示:
0 <= nums.length <= 105-109 <= nums[i] <= 109
解题思路
通过哈希集合存储整数,以快速判断是否存在相邻数字,从而高效地找出数组中的最长连续序列
1: 首先将数组中的所有元素放入到 HashSet 中,去除掉重复元素。并用于后续常数级别的查询操作。
2: 遍历整个HashSet,首先判断当前元素-1 的值是否在 HashSet中,如果不存在,才有可能是一个连续的序列。
3: 如果第一个元素-1 的值 不在 HahSet 中,则记录当前的值,循环查询当前值+1 的值是否在 HashSet中。如果存在,则连续序列的长度+1。
4: 最后计算连续序列的最大值。
解题代码
class Solution {public int longestConsecutive(int[] nums) {Set<Integer> numSet = new HashSet<Integer>();for (int i : nums) {numSet.add(i);}int longStreak = 0;for (int num : numSet ) {if (!numSet.contains(num -1)) {int currentNum = num;int currentStreak = 1;while (numSet.contains(currentNum + 1 )) {currentNum +=1;currentStreak +=1;}longStreak = Math.max(longStreak,currentStreak);}}return longStreak;}
}
以上就是最长连续序列的解题过程。除了上面的解题思路,官方网站上也有其他大神的解题思路。
传送链接如下:
https://leetcode.cn/problems/longest-consecutive-sequence/solutions/?envType=study-plan-v2&envId=top-100-liked
相关文章:

LeetCode 128: 最长连续序列
LeetCode 128: 最长连续序列 题目: 给定一个未排序的整数数组 nums ,找出数字连续的最长序列(不要求序列元素在原数组中连续)的长度。 请你设计并实现时间复杂度为 O(n) 的算法解决此问题。 示例 1: 输入:nums […...

大语言模型需要的可观测性数据的关联方式
可观测性数据的关联方式及其优缺点 随着现代分布式架构和微服务的普及,可观测性(Observability)已经成为确保系统健康、排查故障、优化性能的重要组成部分。有效的可观测性数据关联方式不仅能够帮助我们实时监控系统的运行状态,还…...

【韩顺平linux】部分上课笔记整理
整理一下一些韩顺平老师上课时候的笔记 课程:【小白入门 通俗易懂】韩顺平 一周学会Linux linux环境:使用阿里云服务器 笔记参考 : [学习笔记]2021韩顺平一周学会Linux 一、自定义函数 基本语法 应用实例: 计算两个参数的和…...

python调用pc的语音借口
先安装: pip install pyttsx3再运行: import pyttsx3 # 初始化语音引擎 def init_engine():engine pyttsx3.init()# 设置中文语音voices engine.getProperty(voices)for voice in voices:if chinese in voice.name.lower():engine.setProperty(voice…...

【Golang学习之旅】Golang 内存管理与 GC 机制详解
文章目录 前言1. Go 语言的内存管理的简述2. Golang 内存管理机制2.1 Go 语言的内存分配模型2.2 Go 变量分配示例2.3 Go 语言的内存池(sync.Pool) 3. Golang 垃圾回收(GC)机制详解3.1 Go 的 GC 机制概述3.2 GC 触发条件3.3 手动触…...

Kamailio 各个功能的共同点、不同点及应用场景
Kamailio 各个功能的共同点、不同点及应用场景: 功能共同点不同点应用场景SIP 注册服务器处理用户注册请求,维护用户位置信息专注于用户设备的注册和注销,维护设备位置企业内部通信系统,确保用户设备的动态注册和注销SIP 代理服务…...
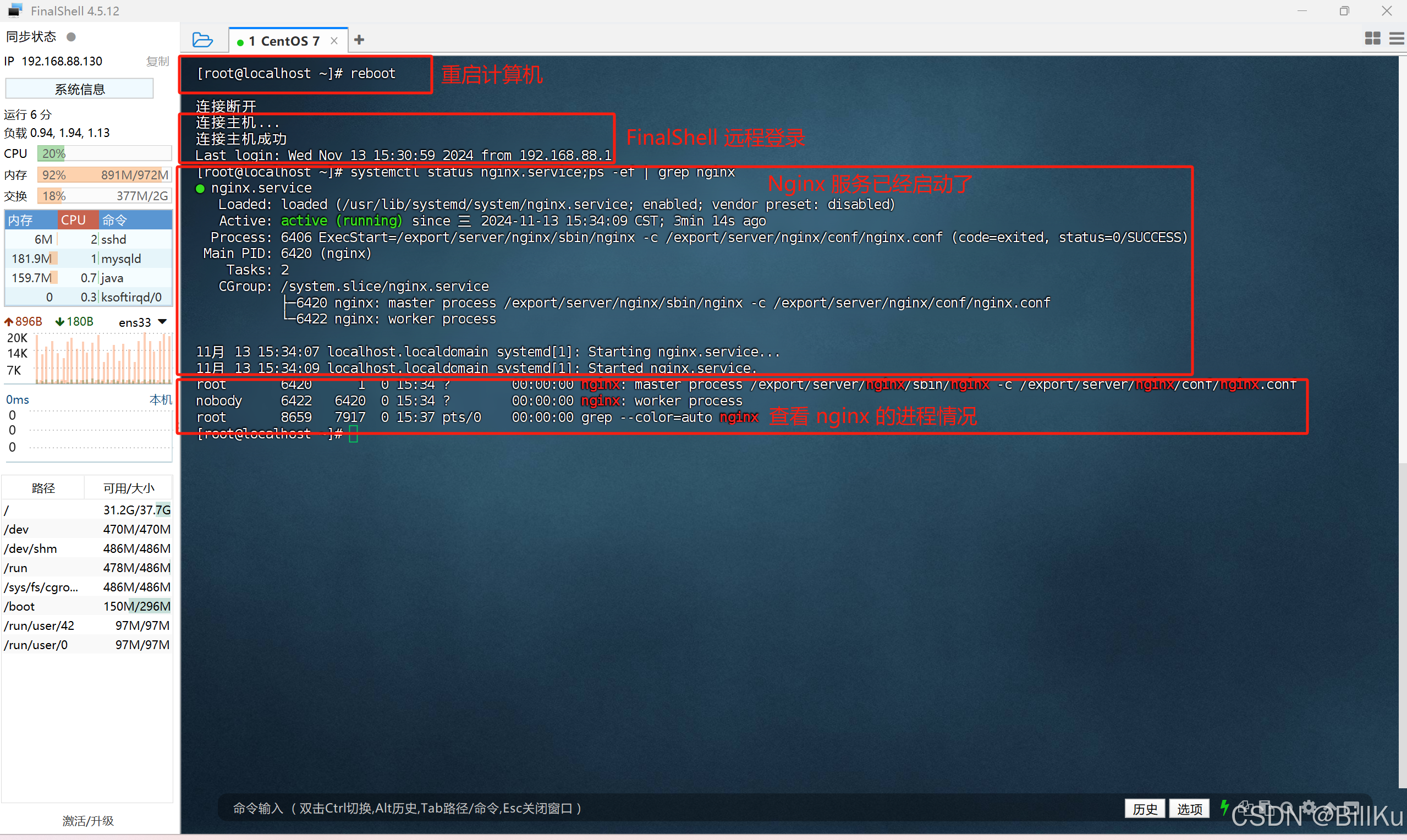
Linux(CentOS)安装 Nginx
CentOS版本:CentOS 7 Nginx版本:1.24.0 两种安装方式: 一、通过 yum 安装,最简单,一键安装,全程无忧。 二、通过编译源码包安装,需具备配置相关操作。 最后附:设置 Nginx 服务开…...

string 与 wstring 的字符编码
测试代码: #include<stdio.h> #include<stdlib.h> #include<windows.h> #include <locale.h> #include <string> #include <iostream>// 函数用于计算UTF-8字符串中的字符数 int utf8_strlen(const char* str) {int len = 0;for (; *s…...

C#面试常考随笔14: 方法如何传递不定数量的参数?params关键字怎么使用?
使用params关键字,就可以像python传参那样传递多个参数,类似元组 主要作用 params 关键字的主要作用是让方法可以接受不定数量的参数,而不需要在调用方法时显式地创建数组来传递多个参数。这为方法调用提供了更大的灵活性,使得代…...

开发一款类似《王者荣耀》的游戏是一个复杂的系统工程,涉及多个领域的知识和技术。以下是从多个角度详细阐述如何开发的思维。
一、明确游戏定位与核心玩法 游戏类型 MOBA(Multiplayer Online Battle Arena):强调团队合作、策略性和即时战斗。确定游戏模式(如5v5、3v3等)和地图设计。 核心玩法 角色设计:英雄技能、属性、成长曲线。…...

VMware下Linux和macOS安装VSCode一些总结
本文介绍VMware下Linux和macOS安装VSCode的一些内容,包括VSCode编译器显示中文以及安装.NET环境和Python环境。 VSCode下载地址:Download Visual Studio Code - Mac, Linux, Windows 一.Linux系统下 1.安装中文包 按 Ctrl Shift P 打开命令面板。输…...

aspectFill(填充目标区域的同时保持图像的原有宽高比 (aspect ratio)图像不会被拉伸或压缩变形
“aspectFill” 是一个常用于图像和视频处理的术语,尤其是在用户界面 (UI) 设计和图形编程领域。它描述的是一种图像缩放或调整大小的方式,旨在填充目标区域的同时保持图像的原有宽高比 (aspect ratio)。 更详细的解释: Aspect Ratio (宽高比): 指的是图…...

我的年度写作计划
目录 计算机经典四件 数据结构 计算机网络体系 经典操作系统与计算机架构 嵌入式领域笔记 其他部分 私货部分 笔者打算在这里理一下今年的写作计划,如下所示: 计算机经典四件 数据结构 笔者因为冲刺面试需要,还是要更加扎实的掌握自…...
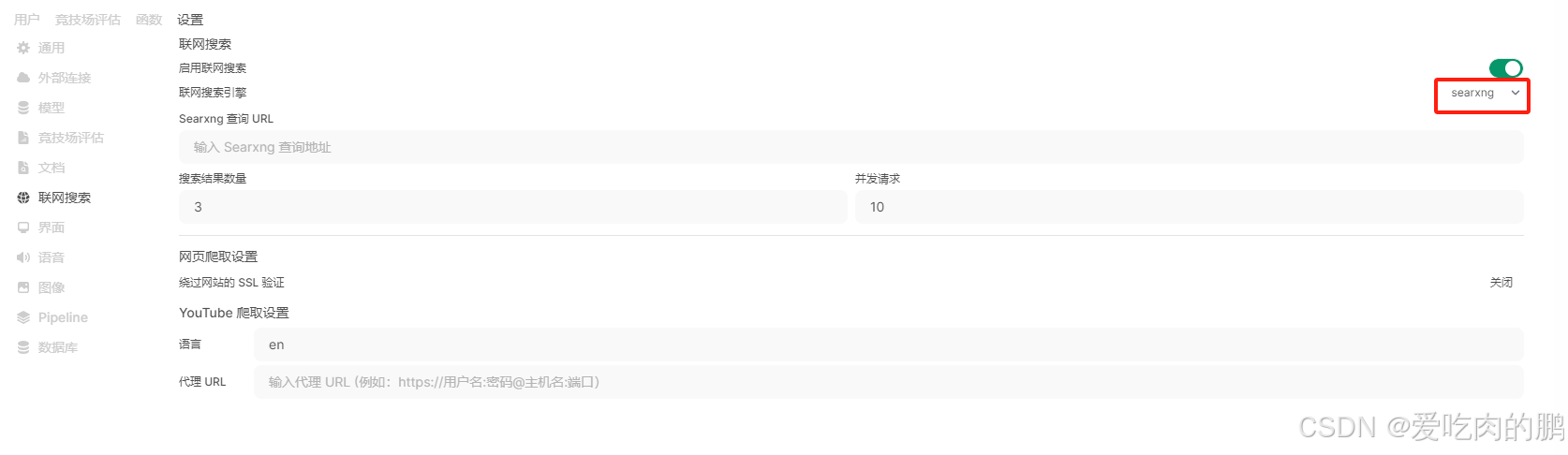
DeepSeek与llama本地部署(含WebUI)
DeepSeek从2025年1月起开始火爆,成为全球最炙手可热的大模型,各大媒体争相报道。我们可以和文心一言一样去官网进行DeepSeek的使用,那如果有读者希望将大模型部署在本地应该怎么做呢?本篇文章将会教你如何在本地傻瓜式的部署我们的…...
全面解析)
SOA(面向服务架构)全面解析
1. 引言 什么是SOA(面向服务架构) SOA(Service-Oriented Architecture,面向服务架构)是一种将应用程序功能以“服务”的形式进行模块化设计的架构风格。这些服务是独立的功能模块,它们通过定义明确的接口…...

PyQt6/PySide6 的 QDialog 类
QDialog 是 PyQt6 或 PySide6 库中用于创建对话框的类。对话框是一种特殊的窗口,通常用于与用户进行短期交互,如输入信息、显示消息或选择选项等。QDialog 提供了丰富的功能和灵活性,使得开发者可以轻松地创建各种类型的对话框。下面我将详细…...

mes系统对工业数字化转型起到重要作用,它的实际应用有哪些
一、生产计划与调度 在工业数字化转型中,MES 系统能够对生产计划进行高效的管理和调度。通过与企业资源计划(ERP)系统的集成,MES 可以获取生产订单信息,并根据生产设备的状态、人员安排以及物料供应情况等因素&#x…...

Qt:项目文件解析
目录 QWidget基础项目文件解析 .pro文件解析 widget.h文件解析 widget.cpp文件解析 widget.ui文件解析 main.cpp文件解析 认识对象模型 窗口坐标系 QWidget基础项目文件解析 .pro文件解析 工程新建好之后,在工程目录列表中有⼀个后缀为 ".pro" …...

【学术投稿】第五届计算机网络安全与软件工程(CNSSE 2025)
重要信息 官网:www.cnsse.org 时间:2025年2月21-23日 地点:中国-青岛 简介 第五届计算机网络安全与软件工程(CNSSE 2025)将于2025年2月21-23日在中国-青岛举行。CNSSE 2025专注于计算机网络安全、软件工程、信号处…...

Java 大视界 -- Java 大数据在智能供应链中的应用与优化(76)
💖亲爱的朋友们,热烈欢迎来到 青云交的博客!能与诸位在此相逢,我倍感荣幸。在这飞速更迭的时代,我们都渴望一方心灵净土,而 我的博客 正是这样温暖的所在。这里为你呈上趣味与实用兼具的知识,也…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...
