【力扣】138.随机链表的复制
AC截图

题目


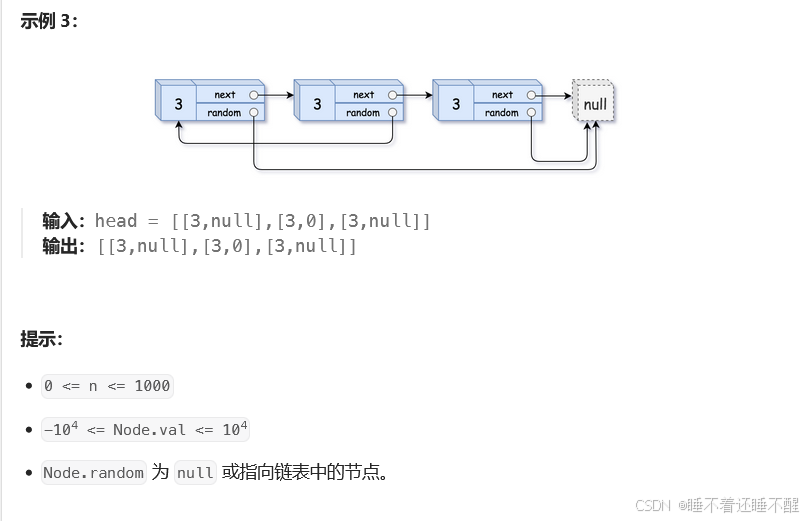
代码
使用哈希存储<旧节点,新结点>
/*
// Definition for a Node.
class Node {
public:int val;Node* next;Node* random;Node(int _val) {val = _val;next = NULL;random = NULL;}
};
*/class Solution {
public:Node* copyRandomList(Node* head) {if(head==NULL){return NULL;}unordered_map<Node*,Node*> map;Node* p=head;while(p!=NULL){map[p]=new Node(p->val);p=p->next;} p=head;while(p!=NULL){map[p]->next = map[p->next];map[p]->random = map[p->random];p=p->next;}p=head;return map[p];}
};相关文章:

【力扣】138.随机链表的复制
AC截图 题目 代码 使用哈希存储<旧节点,新结点> /* // Definition for a Node. class Node { public:int val;Node* next;Node* random;Node(int _val) {val _val;next NULL;random NULL;} }; */class Solution { public:Node* copyRandomList(Node* hea…...

编程语言的深度剖析:从语法到性能优化
引言 随着软件开发的不断进化,编程语言的选择对项目的成功与否具有关键影响。今天的开发者面临着丰富多样的编程语言选择:每一种语言都有独特的优势、特性和适用场景。然而,语言的设计理念、运行机制和优化技巧背后的技术细节却常常被忽视。本…...

台湾精锐APEX减速机在半导体制造设备中的应用案例
半导体制造设备对传动系统的精度、可靠性和稳定性要求极高,台湾精锐APEX减速机凭借其低背隙、高精度和高刚性等优势,在半导体制造设备中得到了广泛应用。 案例一:晶圆切割设备 1.应用场景 在晶圆切割过程中,设备需要高精度的运…...

Rocketmq 和 Rabbitmq ,在多消费者的情况下,可以实现顺序消费吗
在多消费者的情况下,RocketMQ 和 RabbitMQ 都可以实现顺序消费,但它们的实现机制和适用场景有所不同。以下是对两者的详细分析和对比: 1. RocketMQ 的顺序消费 1.1 实现机制 顺序消息:RocketMQ 支持顺序消息(Orderly …...
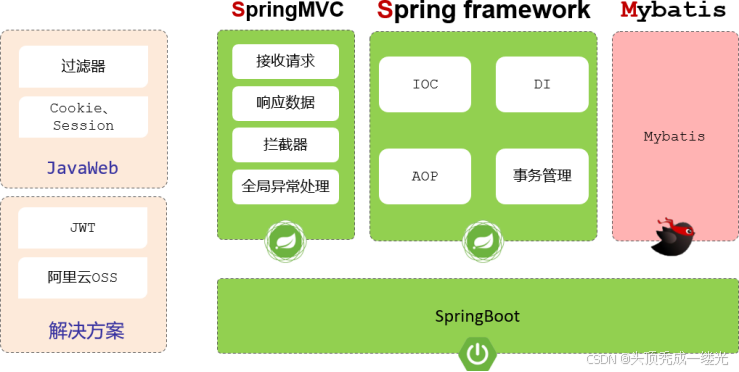
Springboot原理(面试高频)
目录 一、 配置优先级 编辑 二、Bean管理 2.1:获取Bean 编辑 2.2:Bean作用域 2.3:第三方Bean 三、Springboot底层原理 3.1:起步依赖 3.1.1:ma…...
2024 Rust现代实用教程:1.1Rust简介与安装更新
文章目录 一、Rust安装二、更新Rust三、Rust的Stable与Nightly版本四、卸载ubuntu安装的cargo和rustup五、rust源设置六、rust交叉编译工具链说明 rustup稳定版交叉编译步骤 步骤 1:安装目标组件步骤 2:安装交叉编译工具链步骤 3:配置环境变…...
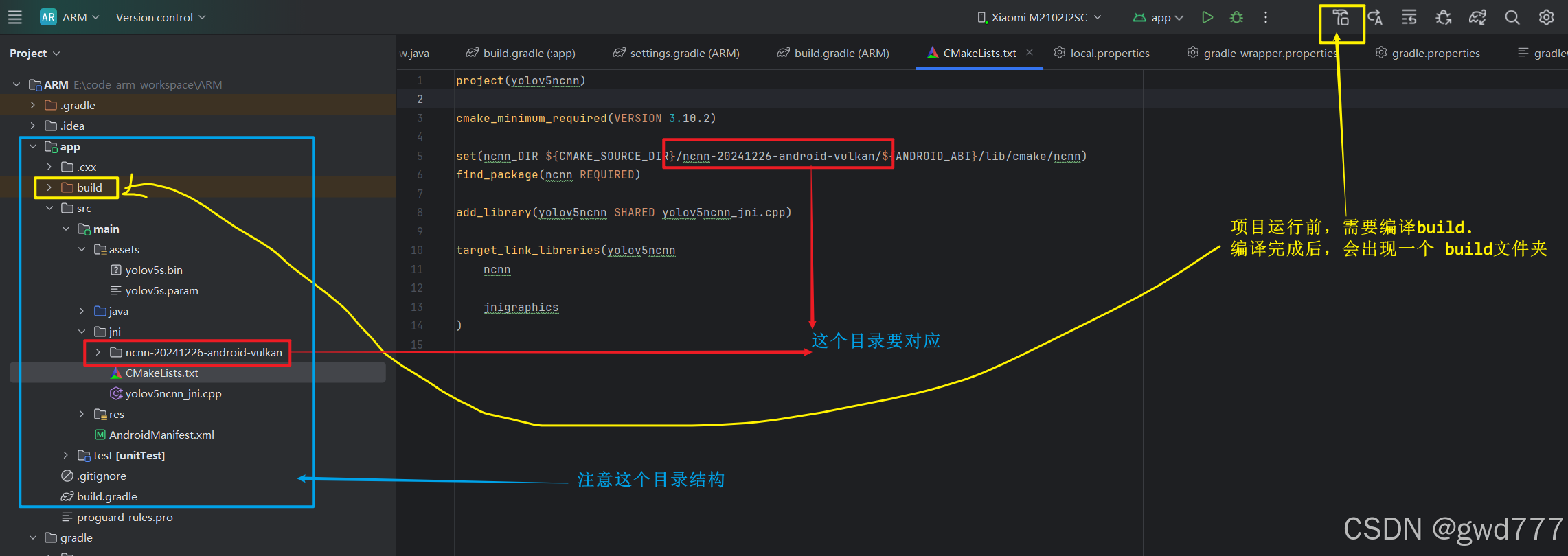
yolov11模型在Android设备上运行【踩坑记录】
0) 参考资料: https://github.com/Tencent/ncnn?tabreadme-ov-file https://github.com/pnnx/pnnx https://github.com/nihui/ncnn-android-yolov5 https://github.com/Tencent/ncnn?tabreadme-ov-file 1) :将xxx.pt模型转化成 xxx.onnx ONNX(Ope…...

提示工程:少样本提示(Few-shot Prompting)
少样本提示(Few-shot Prompting)是一种利用大语言模型从少量示例样本中学习并处理任务的方法。它的核心思想是利用大语言模型的上下文学习能力,通过在提示中增加“示例样本”来启发大语言模型达到举一反三的效果。这种方法避免了重新训练或者…...

方舟字节码原理剖析:架构、特性与实践应用
方舟字节码原理剖析:架构、特性与实践应用 一、引言 在当今软件行业高速发展的大背景下,应用程序的性能、开发效率以及跨平台兼容性成为了开发者们关注的核心要素。编译器作为软件开发流程中的关键工具,其性能和特性直接影响着软件的质量和…...

深入Linux系列之环境变量
深入Linux系列之环境变量 那么在之前的内容中,我们已经介绍了我们Linux进程的一些关键属性,例如进程编号以及进程状态和进程优先级,那么本篇文章接介绍Linux的环境变量这一知识点,那么废话不多说,我们进入环境变量的讲…...

国产编辑器EverEdit - Web预览功能
1 Web预览 1.1 应用场景 在编辑HTML文件时,可以通过EverEdit的Web预览功能,方便用户随时观察和调整HTML代码。 1.2 使用方法 1.2.1 使用EverEdit内部浏览器预览 选择主菜单查看 -> Web预览,或使用快捷键Ctrl B,即可打开Ev…...
,是什么意思)
C#中的Frm_Welcome.Instance.Show(),是什么意思
Frm_Welcome.Instance.Show() 是一种常见的单例模式(Singleton Pattern)实现方式,通常用于在应用程序中确保某个窗体(Form)只有一个实例,并通过该实例显示窗体。以下是对这段代码的详细解释: 代…...

07苍穹外卖之redis缓存商品、购物车(redis案例缓存实现)
课程内容 缓存菜品 缓存套餐 添加购物车 查看购物车 清空购物车 功能实现:缓存商品、购物车 效果图: 1. 缓存菜品 1.1 问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压…...

C++开发(软件开发)常见面试题
目录 1、C里指针和数组的区别 2、C中空指针请使用nullptr不要使用NULL 3、http/https区别和头部结构? 4、有了mac地址为什么还要ip地址?ip地址的作用 5、有了路由器为什么还要交换机? 6、面向对象三大特性 7、友元函数 8、大端小端 …...
结合实现路径规划)
人工智能-A*算法与卷积神经网络(CNN)结合实现路径规划
以下是一个将 A* 算法与卷积神经网络(CNN)结合实现路径规划的代码示例。主要思路是使用 A* 算法生成训练数据,然后用这些数据训练一个 CNN 模型,让 CNN 学习如何预测路径,最后使用训练好的 CNN 模型进行路径规划。 代码实现 import numpy as np import heapq import tor…...

蓝桥杯备赛——进制转化相关问题
目录 一、基础概念 二、问题研究(1) 代码解读: 1. transfer 函数 代码功能概述 详细步骤 2. main 函数 代码功能概述 详细步骤 三、运用递归解决 (一) 代码如下: 代码解读: &#…...

DevOps的个人学习
一、DevOps介绍 软件开发最初是由两个团队组成: 开发团队:负责设计和构建系统。运维团队:负责测试代码后部署上线,确保系统稳定安全运行。 这两个看似目标不同的团队需要协同完成一个软件的开发。DevOps整合了开发与运维团队&a…...

使用Pytorch训练一个图像分类器
一、准备数据集 一般来说,当你不得不与图像、文本或者视频资料打交道时,会选择使用python的标准库将原始数据加载转化成numpy数组,甚至可以继续转换成torch.*Tensor。 对图片而言,可以使用Pillow库和OpenCV库对视频而言…...

《ARM64体系结构编程与实践》学习笔记(四)
MMU内存管理 1.MMU内存管理(armv8.6手册的D5章节),MMU包含快表TLB,TLB是对页表的部分缓存,页表是存放在内存里面的。 AArch64仅仅支持Long Descriptor的页表格式,AArch32支持两种页表格式Armv7-A Short De…...

01-SDRAM控制器的设计——案例总概述
本教程重点▷▷▷ 存储器简介。 介绍 SDRAM 的工作原理。 详细讲解SDRAM 控制的Verilog 实现方法。 PLL IP和FIFO IP 的调用,计数器设计,按键边沿捕获,数码管控制。 完成SDRAM控制器应用的完整案例。 Signal Tap 调试方法。 准备工作▷…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...

WebRTC从入门到实践 - 零基础教程
WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC? WebRTC(Web Real-Time Communication)是一个支持网页浏览器进行实时语音…...

Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析
Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析 一、第一轮基础概念问题 1. Spring框架的核心容器是什么?它的作用是什么? Spring框架的核心容器是IoC(控制反转)容器。它的主要作用是管理对…...
