Foundation CSS 可见性
Foundation CSS 可见性
引言
在网页设计中，CSS可见性是一个至关重要的概念。它决定了元素在网页上是否可见，以及如何显示。Foundation CSS 是一个流行的前端框架，它提供了丰富的工具和组件来帮助开发者构建响应式和可访问的网页。本文将深入探讨 Foundation CSS 中的可见性相关属性，帮助开发者更好地理解和应用这些属性。
一、CSS 可见性概述
CSS 可见性主要涉及到以下几个概念：
- 可见性（Visibility）：元素是否可见。
- 隐藏（Hidden）：元素不可见，但仍然占据空间。
- 透明度（Opacity）：元素可见，但可以半透明。
在 Foundation CSS 中，这些概念通过以下属性实现：
display：控制元素的显示方式。visibility：控制元素的可见性。opacity：控制元素的透明度。
二、display 属性
display 属性是控制元素显示方式的关键属性。在 Foundation CSS 中，常见的 display 属性值包括：
block：块级元素，占据整个父元素宽度。inline-block：行内块级元素，可以设置宽度和高度。
相关文章：
Foundation CSS 可见性
Foundation CSS 可见性 引言 在网页设计中，CSS可见性是一个至关重要的概念。它决定了元素在网页上是否可见，以及如何显示。Foundation CSS 是一个流行的前端框架，它提供了丰富的工具和组件来帮助开发者构建响应式和可访问的网页。本文将深入探讨 Foundation CSS 中的可见性…...
7. Docker 容器数据卷的使用(超详细的讲解说明)
7. Docker 容器数据卷的使用(超详细的讲解说明) 文章目录 7. Docker 容器数据卷的使用(超详细的讲解说明)1. Docker容器数据卷概述2. Docker 容器数据卷的使用演示：2.1 宿主 和 容器之间映射添加容器卷2.2 容器数据卷 读写规则映射添加说明2.3 容器数据卷的继承和共…...
算法——结合实例了解广度优先搜索(BFS)搜索
一、广度优先搜索初印象 想象一下，你身处一座陌生的城市，想要从当前位置前往某个景点，你打开手机上的地图导航软件，输入目的地后，导航软件会迅速规划出一条最短路线。这背后，就可能运用到了广度优先搜索&am…...
qt QCommandLineOption 详解
1、概述 QCommandLineOption类是Qt框架中用于解析命令行参数的类。它提供了一种方便的方式来定义和解析命令行选项，并且可以与QCommandLineParser类一起使用，以便在应用程序中轻松处理命令行参数。通过QCommandLineOption类，开发者可以更便捷…...
Linux权限提升-内核溢出
一：Web到Linux-内核溢出Dcow 复现环境：https://www.vulnhub.com/entry/lampiao-1,249/ 1.信息收集：探测⽬标ip及开发端⼝ 2.Web漏洞利⽤： 查找drupal相关漏洞 search drupal # 进⾏漏洞利⽤ use exploit/unix/webapp/drupal_dr…...
【环境安装】重装Docker-26.0.2版本
【机器背景说明】Linux-Centos7；已有低版本的Docker 【目标环境说明】 卸载已有Docker，用docker-26.0.2.tgz安装包安装 1.Docker包下载 下载地址：Index of linux/static/stable/x86_64/ 2.卸载已有的Docker 卸载之前首先停掉服务 sudo…...
【云安全】云原生- K8S API Server 未授权访问
API Server 是 Kubernetes 集群的核心管理接口，所有资源请求和操作都通过 kube-apiserver 提供的 API 进行处理。默认情况下，API Server 会监听两个端口：8080 和 6443。如果配置不当，可能会导致未授权访问的安全风险。 8080 端口…...
笔记7——条件判断
条件判断 主要通过 if、elif 和 else 语句来实现 语法结构 # if 条件1: # 条件1为真时执行的代码 # elif 条件2： # 条件1为假、且条件2为真时执行的代码 # elif 条件3： # 条件1、2为假、且条件3为真时执行的代码 # ... # else: # 所…...
Word 公式转 CSDN 插件 发布
经过几个月的苦修，这款插件终于面世了。 从Word复制公式到CSDN粘贴，总是出现公式中的文字被单独提出来，而公式作为一个图片被粘贴的情况。公式多了的时候还会导致CSDN禁止进一步的上传公式。 经过对CSDN公式的研究，发现在粘贴公…...
二次封装axios解决异步通信痛点
为了方便扩展，和增加配置的灵活性，这里将通过封装一个类来实现axios的二次封装,要实现的功能包括： 为请求传入自定义的配置，控制单次请求的不同行为在响应拦截器中对业务逻辑进行处理，根据业务约定的成功数据结构，返回业务数据对响应错误进行处理，配置显示对话框或消息形…...
算法——结合实例了解深度优先搜索（DFS）
一，深度优先搜索（DFS）详解 DFS是什么？ 深度优先搜索（Depth-First Search，DFS）是一种用于遍历或搜索树、图的算法。其核心思想是尽可能深地探索分支，直到无法继续时回溯到上一个节点…...
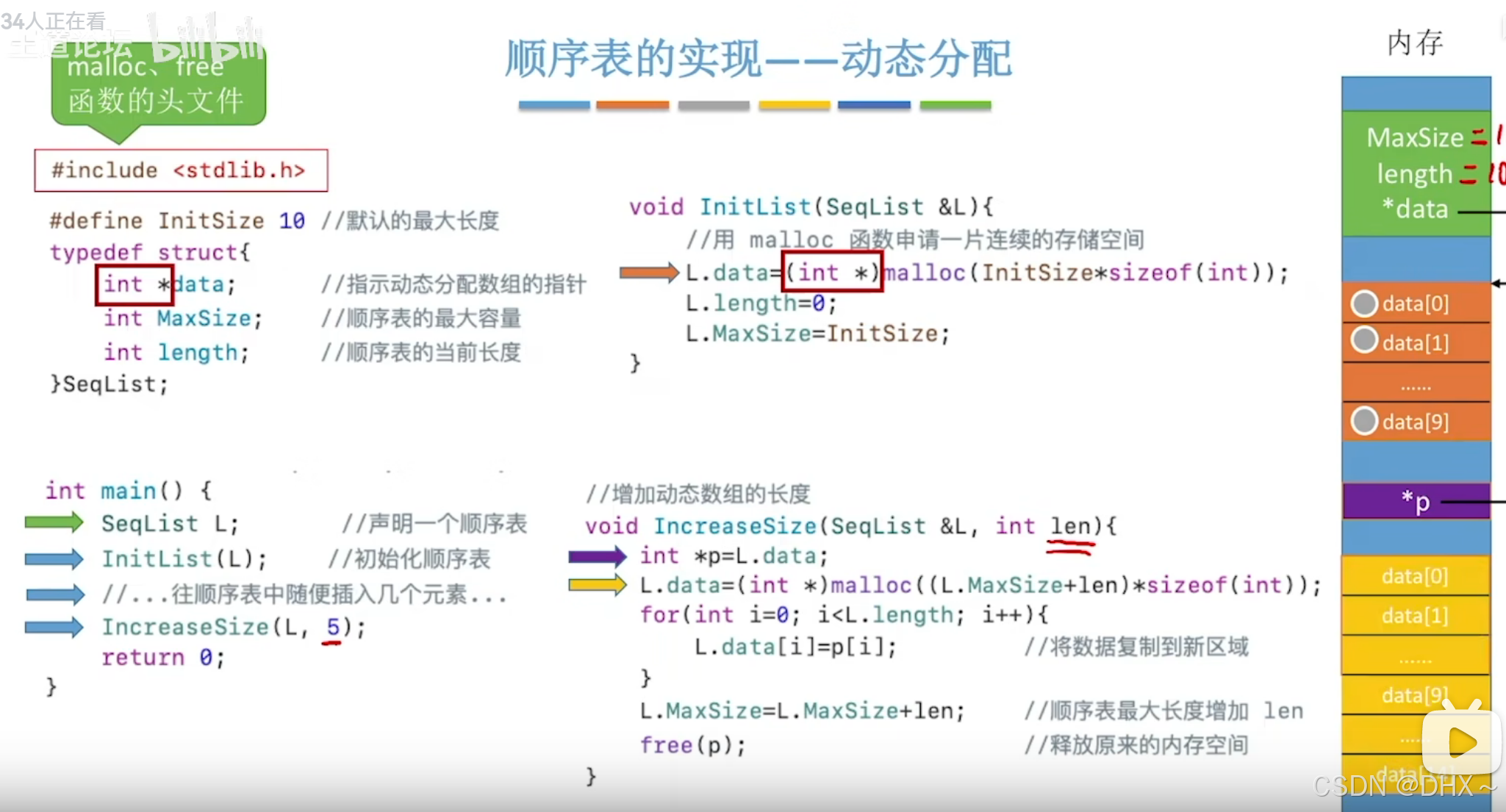
数据结构（考研）
线性表 顺序表 顺序表的静态分配 //线性表的元素类型为 ElemType//顺序表的静态分配 #define MaxSize10 typedef int ElemType; typedef struct{ElemType data[MaxSize];int length; }SqList;顺序表的动态分配 //顺序表的动态分配 #define InitSize 10 typedef struct{El…...
使用SSE协议进行服务端向客户端主动发送消息
1.创建一个SSE配置类: 1.1代码如下：package com.campus.platform.config;import org.springframework.context.annotation.Bean; import org.springframework.context.annotation.Configuration; import org.springframework.web.servlet.config.annotation.AsyncS…...
FastAPI 高并发与性能优化
FastAPI 高并发与性能优化 目录 🚀 高并发应用设计原则🧑💻 异步 I/O 优化 Web 服务响应速度⏳ 在 FastAPI 中优化异步任务执行顺序🔒 高并发中的共享资源与线程安全问题 1. 🚀 高并发应用设计原则 在构建高并发应…...
DFS+回溯+剪枝（深度优先搜索）——搜索算法
目录 一、递归 1.什么是递归？ 2.什么时候使用递归？ 3.如何理解递归？ 4.如何写好递归？ 二、记忆化搜索（记忆递归） 三、回溯 四、剪枝 五、综合试题 1.N皇后 2.解数独 DFS也就是深度优先搜索&am…...
在cursor/vscode中使用godot C#进行游戏开发
要在 Visual Studio Code(VS Code)中启动 C#Godot 项目，可以按照以下步骤进行配置： 1.安装必要的工具 • 安装 Visual Studio Code：确保你已经安装了最新版本的 VS Code。 • 安装.NET SDK：下载并安装.NET 7.x SDK（…...
vant4 van-list组件的使用
<van-listv-if"joblist && joblist.length > 0"v-model:loading"loading":finished"finished":immediate-check"false"finished-text"没有更多了"load"onLoad">// 加载 const loading ref(fals…...
介绍 Liquibase、Flyway、Talend 和 Apache NiFi：选择适合的工具
在现代软件开发中，尤其是在数据库管理和数据集成方面，选择合适的工具至关重要。本文将介绍四个流行的工具：Liquibase、Flyway、Talend 和 Apache NiFi，分析它们的应用、依赖以及如何选择适合的工具。 1. Liquibase 简介ÿ…...
攻防世界33 catcat-new【文件包含/flask_session伪造】
题目： 点击一只猫猫： 看这个url像是文件包含漏洞，试试 dirsearch扫出来/admin，访问也没成功（--delay 0.1 -t 5） 会的那几招全用不了了哈哈，那就继续看答案 先总结几个知识点 1./etc/passwd&am…...
Git -＞ Git配置密钥对，并查看公钥
Git密钥对的核心作用 私钥 (id_rsa) 你的数字身份证：存放在本机 ~/.ssh 目录下必须严格保密（类似银行卡密码），不可泄露或共享用于 解密 来自服务器的加密信息 公钥 (id_rsa.pub) 可公开的验证锁：需要上传到 Git 服…...
SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了：一行…...
电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时，可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案： 1. 检查电源供电问题 问题原因：多块移动硬盘同时运行可能导致USB接口供电不足&#x…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达，从日常对话到特定领域的文档（例如医学文档）（Heritage 2013；Landmark、Gulbrandsen 和 Svenevei…...
LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣（LeetCode） 思路 右视图是指从树的右侧看，对于每一层，只能看到该层最右边的节点。实现思路是： 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...
C++.OpenGL （14/64）多光源（Multiple Lights）
多光源（Multiple Lights） 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...
Scrapy-Redis分布式爬虫架构的可扩展性与容错性增强：基于微服务与容器化的解决方案
在大数据时代，海量数据的采集与处理成为企业和研究机构获取信息的关键环节。Scrapy-Redis作为一种经典的分布式爬虫架构，在处理大规模数据抓取任务时展现出强大的能力。然而，随着业务规模的不断扩大和数据抓取需求的日益复杂，传统…...
LCTF液晶可调谐滤波器在多光谱相机捕捉无人机目标检测中的作用
中达瑞和自2005年成立以来，一直在光谱成像领域深度钻研和发展，始终致力于研发高性能、高可靠性的光谱成像相机，为科研院校提供更优的产品和服务。在《低空背景下无人机目标的光谱特征研究及目标检测应用》这篇论文中提到中达瑞和 LCTF 作为多…...
 Module Federation：Webpack.config.js文件中每个属性的含义解释)
MFE(微前端) Module Federation：Webpack.config.js文件中每个属性的含义解释
以Module Federation 插件详为例，Webpack.config.js它可能的配置和含义如下： 前言 Module Federation 的Webpack.config.js核心配置包括： name filename（定义应用标识） remotes（引用远程模块࿰…...
ubuntu22.04有线网络无法连接，图标也没了
今天突然无法有线网络无法连接任何设备，并且图标都没了 错误案例 往上一顿搜索，试了很多博客都不行，比如 Ubuntu22.04右上角网络图标消失 最后解决的办法 下载网卡驱动，重新安装 操作步骤 查看自己网卡的型号 lspci | gre…...
若依登录用户名和密码加密
/*** 获取公钥：前端用来密码加密* return*/GetMapping("/getPublicKey")public RSAUtil.RSAKeyPair getPublicKey() {return RSAUtil.rsaKeyPair();}新建RSAUti.Java package com.ruoyi.common.utils;import org.apache.commons.codec.binary.Base64; im…...