算法——结合实例了解深度优先搜索(DFS)
一,深度优先搜索(DFS)详解
DFS是什么?
深度优先搜索(Depth-First Search,DFS)是一种用于遍历或搜索树、图的算法。其核心思想是尽可能深地探索分支,直到无法继续时回溯到上一个节点,尝试其他分支。DFS的实现通常基于递归或**栈(后进先出)**结构,适合解决路径存在性、状态可达性问题,但不保证找到最短路径。
与BFS的区别:
- BFS逐层展开,适合找最短路径。
- DFS沿单一分支深入,可能更快找到解,但路径不一定最短。
DFS实现步骤
以递归实现为例,步骤如下:
- 终止条件:检查当前节点是否为目标(如到达终点)。
- 标记访问:将当前节点标记为已访问,避免重复处理。
- 递归探索:遍历当前节点的所有相邻节点,对未访问的节点递归调用DFS。
栈实现步骤:
- 将起始节点压入栈。
- 循环执行以下操作直到栈空:
- 弹出栈顶节点。
- 若未访问,标记为已访问并处理。
- 将该节点的未访问相邻节点压入栈。
注意事项
1. 剪枝优化
在深度优先搜索中,剪枝是一种非常重要的优化策略。它的核心思想是在搜索过程中,判断某些路径是否不可能到达终点,如果确定不可能,则提前终止对这条路径的搜索,从而减少不必要的计算量,提高搜索效率 。以走迷宫为例,假设我们在迷宫中搜索从起点到终点的路径,当我们走到某个位置时,通过计算发现从这个位置无论怎么走,剩余的步数都无法到达终点(比如剩余的步数小于从当前位置到终点的曼哈顿距离),那么就可以直接放弃对这个位置后续路径的搜索 ,这就是一种简单的剪枝操作。再比如,在一个复杂的迷宫中,如果我们已经走过了一条很长的死胡同,那么当再次遇到类似的路径开头时,就可以直接判断这条路径很可能也是死胡同,从而提前剪枝 。剪枝可以大大减少搜索的空间和时间复杂度,尤其是在处理大规模问题时,效果更为显著 。
2. 避免重复访问
在 DFS 中,标记已访问节点是至关重要的。如果不标记已访问节点,当搜索到一个节点时,可能会不断地重复访问它,从而陷入死循环 。比如在一个图结构中,如果存在环,不标记已访问节点就会导致在环上无限循环 。为了避免这种情况,我们通常使用一个数组或集合来记录节点的访问状态 。在走迷宫的例子中,我们使用二维布尔数组visited来记录每个位置是否被访问过 ,当访问一个新位置时,首先检查visited数组中对应位置的值,如果为true,则说明该位置已经被访问过,不再进行处理;如果为false,则将其标记为true,并继续进行搜索 。在处理图的 DFS 时,也可以使用一个哈希集合来记录已访问的节点,这样可以快速判断一个节点是否已经被访问过 。避免重复访问不仅可以防止死循环,还可以提高搜索效率,因为不需要对已经访问过的节点进行重复处理 。
3. 边界条件处理
在实现 DFS 时,仔细考虑边界条件是确保程序正确性和稳定性的关键 。边界条件包括节点超出范围、数组越界等情况 。以走迷宫为例,在判断一个位置是否可以访问时,需要检查该位置的坐标是否在迷宫的范围内 。如果迷宫是一个n * m的二维数组,那么位置(x, y)必须满足0 <= x < n且0 <= y < m,否则就超出了边界 。在马走日的例子中,当计算马的下一步位置时,同样要检查新位置是否在棋盘内 。如果不处理这些边界条件,程序可能会访问到非法的内存位置,导致运行时错误,如数组越界异常等 。因此,在编写 DFS 代码时,一定要在递归调用之前,仔细检查边界条件,确保程序的健壮性 。
二,实例解析
实例1:中国象棋中马的日字形移动

问题描述:
马从起点 (x, y) 出发,按“日”字形移动(横向±1且纵向±2,或横向±2且纵向±1),判断能否到达目标点 (tx, ty),并统计路径数。
DFS实现步骤:
- 定义方向:8种可能的移动方向:
directions = [ (2,1), (1,2), (-1,2), (-2,1),(-2,-1), (-1,-2), (1,-2), (2,-1) ] - 递归终止条件:当前位置等于目标位置时返回成功。
- 遍历所有方向:对每个方向计算新位置
(nx, ny),检查是否在棋盘内且未访问。 - 回溯恢复状态:递归返回后,将当前位置标记为未访问,以允许其他路径经过。
示例代码(伪代码):
def dfs(x, y, visited, target):if (x, y) == target:return 1 # 找到一条路径count = 0visited[x][y] = Truefor dx, dy in directions:nx, ny = x + dx, y + dyif 0 <= nx < 8 and 0 <= ny < 8 and not visited[nx][ny]:count += dfs(nx, ny, visited, target)visited[x][y] = False # 回溯return count
实例2:走迷宫

问题描述:
从迷宫起点 (0, 0) 出发,寻找一条到达终点 (m-1, n-1) 的路径。迷宫用二维数组 grid 表示,0 为通路,1 为墙。
DFS实现步骤:
- 定义方向:上下左右四个移动方向。
directions = [ (-1,0), (1,0), (0,-1), (0,1) ] - 递归终止条件:当前位置为终点时记录路径。
- 剪枝无效路径:跳过越界、撞墙或已访问的位置。
- 回溯恢复状态:递归返回后,将当前位置标记为未访问。
示例代码(伪代码):
def dfs(x, y, path, visited):if (x, y) == (m-1, n-1):print(path)returnfor dx, dy in directions:nx, ny = x + dx, y + dyif 0 <= nx < m and 0 <= ny < n and grid[nx][ny] == 0 and not visited[nx][ny]:visited[nx][ny] = Truepath.append((nx, ny))dfs(nx, ny, path, visited)path.pop()visited[nx][ny] = False
总结与期望

深度优先搜索作为一种基础且强大的搜索算法,在解决各类路径搜索问题中展现出独特的优势。通过马走日和走迷宫这两个实例,我们深入理解了 DFS 的工作原理、实现步骤以及在实际应用中的注意事项 。在马走日的问题中,我们利用 DFS 探索马在棋盘上的所有可能移动路径,计算遍历整个棋盘的途径总数,这体现了 DFS 在处理具有特定规则的移动和状态空间搜索问题上的有效性 。而在走迷宫的场景里,DFS 帮助我们从起点出发,通过不断探索和回溯,寻找通往终点的路径,展示了其在解决复杂空间搜索问题的能力 。
DFS 的核心在于递归探索和回溯机制,这使得它能够全面地搜索所有可能的路径。同时,剪枝优化、避免重复访问和边界条件处理等注意事项,对于提高 DFS 的效率和正确性至关重要 。在未来的学习和实践中,我们可以进一步探索 DFS 在更复杂场景下的应用,比如在图论中寻找连通分量、检测环路等问题 。此外,将 DFS 与其他算法相结合,如与启发式搜索算法结合,可能会产生更高效的解决方案 。随着计算机技术的不断发展,DFS 在人工智能、游戏开发、网络分析等领域的应用前景也将更加广阔 。
相关文章:

算法——结合实例了解深度优先搜索(DFS)
一,深度优先搜索(DFS)详解 DFS是什么? 深度优先搜索(Depth-First Search,DFS)是一种用于遍历或搜索树、图的算法。其核心思想是尽可能深地探索分支,直到无法继续时回溯到上一个节点…...
数据结构(考研)
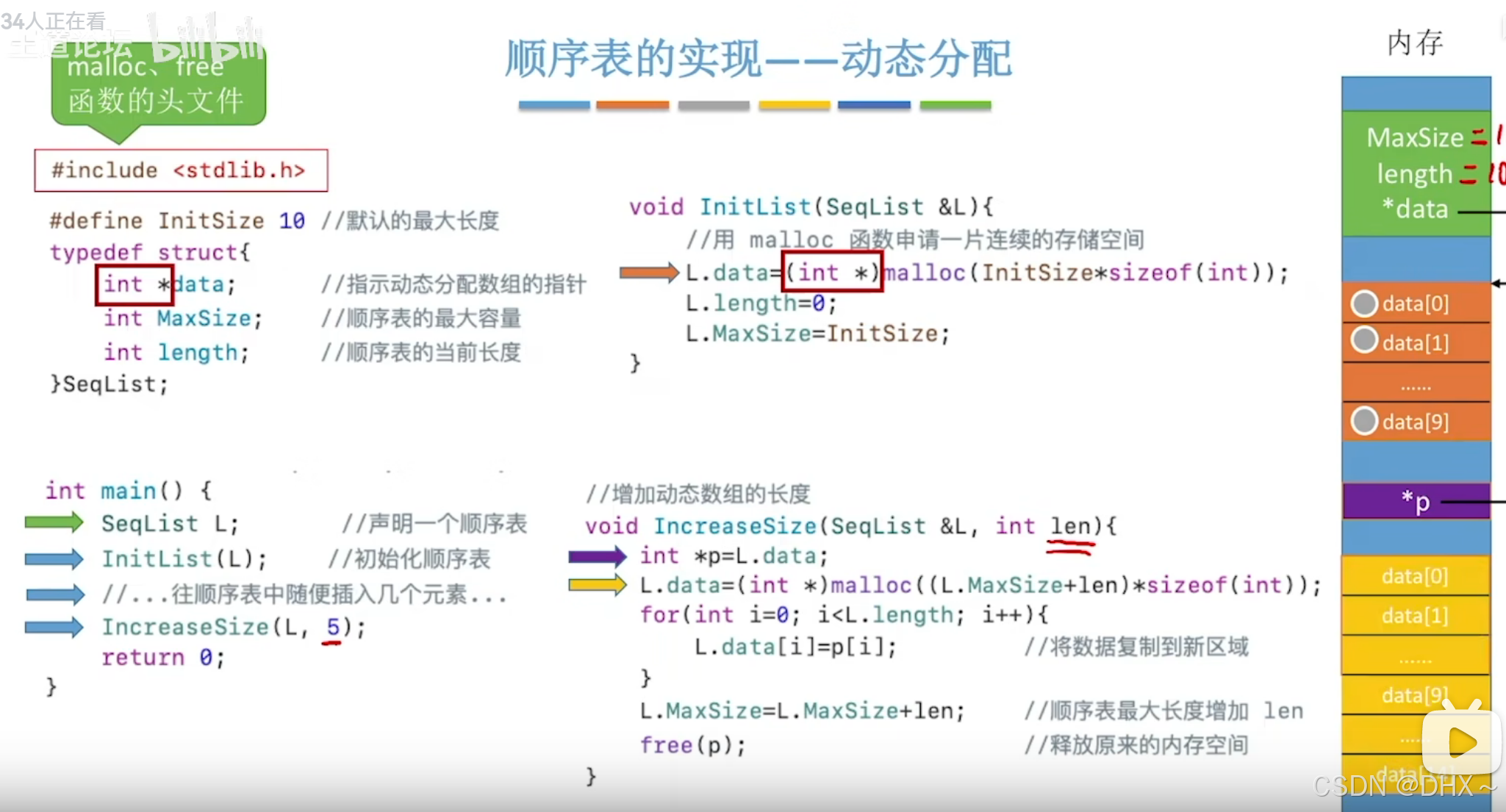
线性表 顺序表 顺序表的静态分配 //线性表的元素类型为 ElemType//顺序表的静态分配 #define MaxSize10 typedef int ElemType; typedef struct{ElemType data[MaxSize];int length; }SqList;顺序表的动态分配 //顺序表的动态分配 #define InitSize 10 typedef struct{El…...

使用SSE协议进行服务端向客户端主动发送消息
1.创建一个SSE配置类: 1.1代码如下:package com.campus.platform.config;import org.springframework.context.annotation.Bean; import org.springframework.context.annotation.Configuration; import org.springframework.web.servlet.config.annotation.AsyncS…...

FastAPI 高并发与性能优化
FastAPI 高并发与性能优化 目录 🚀 高并发应用设计原则🧑💻 异步 I/O 优化 Web 服务响应速度⏳ 在 FastAPI 中优化异步任务执行顺序🔒 高并发中的共享资源与线程安全问题 1. 🚀 高并发应用设计原则 在构建高并发应…...

DFS+回溯+剪枝(深度优先搜索)——搜索算法
目录 一、递归 1.什么是递归? 2.什么时候使用递归? 3.如何理解递归? 4.如何写好递归? 二、记忆化搜索(记忆递归) 三、回溯 四、剪枝 五、综合试题 1.N皇后 2.解数独 DFS也就是深度优先搜索&am…...

在cursor/vscode中使用godot C#进行游戏开发
要在 Visual Studio Code(VS Code)中启动 C#Godot 项目,可以按照以下步骤进行配置: 1.安装必要的工具 • 安装 Visual Studio Code:确保你已经安装了最新版本的 VS Code。 • 安装.NET SDK:下载并安装.NET 7.x SDK(…...

vant4 van-list组件的使用
<van-listv-if"joblist && joblist.length > 0"v-model:loading"loading":finished"finished":immediate-check"false"finished-text"没有更多了"load"onLoad">// 加载 const loading ref(fals…...

介绍 Liquibase、Flyway、Talend 和 Apache NiFi:选择适合的工具
在现代软件开发中,尤其是在数据库管理和数据集成方面,选择合适的工具至关重要。本文将介绍四个流行的工具:Liquibase、Flyway、Talend 和 Apache NiFi,分析它们的应用、依赖以及如何选择适合的工具。 1. Liquibase 简介ÿ…...

攻防世界33 catcat-new【文件包含/flask_session伪造】
题目: 点击一只猫猫: 看这个url像是文件包含漏洞,试试 dirsearch扫出来/admin,访问也没成功(--delay 0.1 -t 5) 会的那几招全用不了了哈哈,那就继续看答案 先总结几个知识点 1./etc/passwd&am…...

Git -> Git配置密钥对,并查看公钥
Git密钥对的核心作用 私钥 (id_rsa) 你的数字身份证:存放在本机 ~/.ssh 目录下必须严格保密(类似银行卡密码),不可泄露或共享用于 解密 来自服务器的加密信息 公钥 (id_rsa.pub) 可公开的验证锁:需要上传到 Git 服…...

淘宝订单列表Fragment转场动画卡顿解决方案
如何应对产品形态与产品节奏相对确定情况下转变为『在业务需求与产品形态高度不确定性的情况下,如何实现业务交付时间与交付质量的确定性』。我们希望通过混合架构(Native 业务容器 Weex 2.0)作为未来交易终端架构的重要演进方向,…...

【ESP32指向鼠标】——icm20948与esp32通信
【ESP32指向鼠标】——icm20948与esp32通信 ICM-20948介绍 ICM-20948 是一款由 InvenSense(现为 TDK 的一部分)生产的 9 轴传感器集成电路。它结合了 陀螺仪、加速度计和磁力计。 内置了 DMP(Digital Motion Processor)即负责执…...

Xcode证书密钥导入
证书干嘛用 渠道定期会给xcode证书,用来给ios打包用,证书里面有记录哪些设备可以打包进去。 怎么换证书 先更新密钥 在钥匙串访问中,选择系统。(选登录也行,反正两个都要导入就是了)。 mac中双击所有 .p12 后缀的密钥ÿ…...

Ubuntu安装PgSQL17
参考官网教程,Ubuntu24 apt在线安装Postgres 17 1. 要手动配置 Apt 存储库 # 导入存储库签名密钥: sudo apt install curl ca-certificates sudo install -d /usr/share/postgresql-common/pgdg sudo curl -o /usr/share/postgresql-common/pgdg/apt…...

K8S容器启动提示:0/2 nodes are available: 2 Insufficient cpu.
问题:K8S的容器启动报错0/2 nodes are available: 2 Insufficient cpu. 原因:Pod的资源请求(requests)设置不当:在Kubernetes中,调度器根据Pod的requests字段来决定哪个节点可以运行该Pod。如果一个Pod声明…...

LabVIEW外腔二极管激光器稳频实验
本项目利用LabVIEW软件开发了一个用于外腔二极管激光器稳频实验的系统。系统能够实现激光器频率的稳定控制和实时监测,为激光实验提供了重要支持。 项目背景: 系统解决了外腔二极管激光器频率不稳定的问题,以满足对激光器频率稳定性要求较高…...

笔记6——字典dict(dictionary)
文章目录 字典dict(dictionary)定义特点常用操作1.访问值2.添加键值对3.修改值4.删除键值对5.遍历字典6.合并字典 性能应用场景dict和list的区别 字典dict(dictionary) 以 键 - 值对 (key - value pairs)的形式存储数据 定义 字典使用花括号 {} 来定义,键和值之…...

【MySQL】InnoDB单表访问方法
目录 1、背景2、环境3、访问类型【1】const【2】ref【3】ref_or_null【4】range【5】index【6】all 4、总结 1、背景 mysql通过查询条件查询到结果的过程就叫访问方法,一条查询语句的访问方法有很多种,接下来我们就来讲一下各种访问方法。 2、环境 创…...

APP端网络测试与弱网模拟!
当前APP网络环境比较复杂,网络制式有2G、3G、4G网络,还有越来越多的公共Wi-Fi。不同的网络环境和网络制式的差异,都会对用户使用app造成一定影响。另外,当前app使用场景多变,如进地铁、上公交、进电梯等,使…...

【个人开发】deepseed+Llama-factory 本地数据多卡Lora微调
文章目录 1.背景2.微调方式2.1 关键环境版本信息2.2 步骤2.2.1 下载llama-factory2.2.2 准备数据集2.2.3 微调模式2.2.4 微调脚本 2.3 踩坑经验2.3.1 问题一:ValueError: Undefined dataset xxxx in dataset_info.json.2.3.2 问题二: ValueError: Target…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...

基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...

go 里面的指针
指针 在 Go 中,指针(pointer)是一个变量的内存地址,就像 C 语言那样: a : 10 p : &a // p 是一个指向 a 的指针 fmt.Println(*p) // 输出 10,通过指针解引用• &a 表示获取变量 a 的地址 p 表示…...

git: early EOF
macOS报错: Initialized empty Git repository in /usr/local/Homebrew/Library/Taps/homebrew/homebrew-core/.git/ remote: Enumerating objects: 2691797, done. remote: Counting objects: 100% (1760/1760), done. remote: Compressing objects: 100% (636/636…...
