C++蓝桥杯基础篇(三)
片头
哈喽!小伙伴们,大家好~,今天我们来学习蓝桥杯基础篇(三),继续练习相关习题,准备好了吗?我们开始啦~

一、while循环
可以简单理解为循环版的if语句。if语句是判断1次,如果条件成立,则执行后面的语句;while是每次判断,如果成立,则执行循环体中的语句,否则停止。
int main() {int i = 0;while (i < 10) {cout << i << endl;i++;}return 0;
}题目1: 求1~100中所有数的立方和
int main() {int sum = 0 , sum2 = 0;int i = 1;while (i <= 100) {sum1 += i * i * i;i++;}cout << "1~100中所有数的立方和为: " << sum << endl;return 0;
}题目2:求斐波那契数列的第n项。f(1)=1,f(2)=1,f(3)=2,f(4)=3,f(n)=f(n-1)+f(n-2)
首先,我们来观察斐波那契数列,规律是:后一个数=前2个数相加
f(1)=1,f(2)=1
f(3)=f(1)+f(2)
f(4)=f(2)+f(3)
f(5)=f(3)+f(4)
.....
f(n)=f(n-2)+f(n-1)
为此,我们可以列出一张表,表示 i,a,b的关系
| i | a | b |
| 0 | f(1) | f(2) |
| 1 | f(2) | f(3) |
| 2 | f(3) | f(4) |
| 3 | f(4) | f(5) |
| 4 | f(5) | f(6) |
| 5 | f(6) | f(7) |
| ... | ... | ... |
| n-3 | f(n-2) | f(n-1) |
| n-2 | f(n-1) | f(n) |
| n-1 | f(n) | f(n+1) |
通过这张表,我们可以看到,i的范围在0~n-2,采用while循环
//求斐波拉契数列的第n项,
//f(1)=1,f(2)=1,f(3)=2,
//f(4)=3,f(5)=5,f(6)=8,f(7)=13,f(8)=21,f(9)=34,f(10)=55//f(1)=1,f(2)=1
//f(3)=f(1)+f(2),
//f(4)=f(2)+f(3),
//f(5)=f(3)+f(4),
//...
//f(n)=f(n-2)+f(n-1)// i a b
// 0 f(1) f(2)
// 1 f(2) f(3)
// 2 f(3) f(4)
// 3 f(4) f(5)
// 4 f(5) f(6)
// 5 f(6) f(7)
// 6 f(7) f(8)
//...
// n-3 f(n-2) f(n-1)
// n-2 f(n-1) f(n)
// n-1 f(n) f(n+1)//当i=n-1时,应该退出循环
//i的取值范围在0~n-2int main() {int i = 0;int n;cin >> n;int a = 1;int b = 1;while (i < n - 1) {int c = a + b;a = b;b = c;i++;}cout << a << endl;return 0;
}死循环:循环永久执行,无法结束。我们要避免写出死循环。
//死循环: 循环永久执行,无法结束。我们要避免写出死循环
int main4() {int x = 1;while (x == 1) puts("!");return 0;
}二、do-while循环
do-while循环不常用。do-while语句与while语句非常相似。唯一的区别:do-while语句限制性循环体后检查条件。不管条件的值如何,我们都要至少执行1次循环。
int main() {int x = 1;while (x < 1) {cout << "x!" << endl;x++;}int y = 1;do {cout << "y!" << endl;} while (y < 1);return 0;
}输出结果:
y!
再来举一个例子:
int main() {int r = 0;int j = 1;while (j <= 10) {r += j;j++;}cout << r << endl;int s = 0;int i = 1;do {s += i;i++;} while (i <= 10);cout << s << endl;return 0;
}可以看到,在控制台中显示的结果相同,均为50
三、for循环
基本思想:把控制循环次数的变量从循环体中剥离
for(init-statement ; condition ; expression)
{
statement
}
init-statement 可以是声明语句、表达式、空语句,一般用来初始化循环变量;
condition 是条件表达式,和 while 中的条件表达式作用一样;可以为空,空语句表示true
expression 一般负责修改循环变量,可以为空
例题1:打印0~9数字
int main() {for (int i = 0; i < 10; i++) {cout << i << endl;}return 0;
}
例题2:求1~100中所有数的立方和
int main() {int sum = 0;for (int j = 1; j <= 100; j++) {sum += j * j * j;}cout << "1~100中所有数的立方和为: " << sum << endl;return 0;
}例题3:求斐波那契数列的第n项。f(1)=1,f(2)=1,f(3)=2,f(4)=3,f(n)=f(n-1)+f(n-2)
//使用for循环实现斐波那契数列
int main() {int a = 1;int b = 1;int n;cin >> n;for (int i = 0; i < n - 1; i++) {int c = a + b;a = b;b = c;}cout << a << endl;return 0;
}此外,init-statement 可以定义多个变量,expression 也可以修改多个变量
例题4:求 1*10 + 2*9 + 3*8 + 4*7 + 5*6
int main() {int sum = 0;int i = 1, j = 10;for (i = 1, j = 10; i < j; i++, j--) {cout << i << "*" << j << endl;sum += i * j;}cout << sum << endl;return 0;
}四、跳转语句
1. break
可以提前从循环中退出,一般与if语句搭配。
例题5:判断一个大于1的数是否为质数(质数:只能被1和自己整除的数)
int main() {int num;cin >> num;bool flag = 1; //假设该数为质数for (int i = 2; i < num; i++) {if (num % i == 0) {flag = 0;break;}}if (flag == 1) {cout << "这个数为质数" << endl;}else {cout << "这个数不是质数" << endl;}return 0;
}2. continue
可以直接跳到当前循环体的结尾。作用和if语句类似。
例题6:求1~100中所有偶数的和
int main() {int i = 1;int sum = 0;for (i = 1; i <= 100; i++) {if (i % 2 == 1)continue;sum += i;}cout << sum << endl;return 0;
}五、多层循环
//多层循环
int main() {//外层循环控制行数//内层循环控制列数for (int i = 0, k = 1; i < 10; i++) {for (int j = 0; j < 10; j++, k++){cout << k << " ";}cout << endl;}return 0;
}结果如下:

我们还可以将代码优化一下:
int main() {int n;cin >> n;for (int i = 1, k = 1; i <= n; i++) {for (int j = 1; j <= n; j++, k++) {printf("%-5d ", k); //左对齐//printf("%5d ", k); //右对齐//cout << k << " ";}cout << endl;}return 0;
}
例题7:打印1~100中的所有质数,并计算质数的数量
//练习: 打印1~100中所有的质数
int main() {int num = 0;for (int i = 1; i <= 100; i++) {bool flag = 1; //假设此时的i为质数for (int j = 2; j < i; j++) {if (i % j == 0) {flag = 0;break;}}if (flag == 1) {cout << i << endl;num++;}}cout << "1~100中所有的质数有" << num << "个" << endl;return 0;
}
例题8:打印正三角
*************************
分析这类题型,我们需要定义3个变量 i,j,k,分别表示行数,空格,以及"*"
比如,我输入n=5,外层循环打印5行,i的取值范围1~n;
接下来观察空格的数量变化:
第1层,空格的数量为4;
第2层,空格的数量为3;
第3层,空格的数量为2;
第4层,空格的数量为1;
第5层,没有打印空格。
通过以上分析,我们得知,空格的数量为 n-i
再来观察"*"的数量变化:
第1层,打印1个"*";
第2层,打印3个"*";
第3层,打印5个"*";
第4层,打印7个"*";
第5层,打印9个"*"。
通过以上分析,我们得知,”*“的数量为 2*i-1
代码如下:
int main() {int n;cin >> n;//外层控制行数for (int i = 1; i <= n ; i++) {//内层循环1控制空格数量for (int j = 1; j <= n-i; j++) {printf(" ");}//内层循环2控制"*"数量for (int k = 1; k <= 2*i-1; k++) {printf("*");}cout << endl;}return 0;
}例题9:打印倒三角
*********
*******
*****
***
*
和上一道题的做法类似,我们依然定义3个变量 i,j,k,分别表示行数,空格,"*"的数量
比如,我输入n=5,则打印5行,i 的取值为 1~n
接下来观察空格的数量,
第1层,没有空格,
第2层,1个空格,
第3层,2个空格,
第4层,3个空格,
第5层,4个空格,
通过上述分析,我们得知,空格的数量为 i-1
再来观察"*"的数量,
第1层,9颗"*",
第2层,7颗"*",
第3层,5颗"*",
第4层,3颗"*",
第5层,1颗"*",
通过上述分析,我们得知,"*"的数量为 2*(n-i)+1
代码如下:
int main() {int n;printf("请输入行号: ");scanf("%d", &n);//外层循环控制行数for (int i = 1; i <= n; i++) {//内层循环1控制空格数量for (int j = 1; j <= i - 1; j++) {printf(" ");}//内层循环2控制"*"数量for (int k = 1; k <= 2 * (n - i) + 1; k++) {printf("*");}cout << endl;}return 0;
}例题10:输入一个n,打印n阶菱形,n为奇数
n = 9 的结果
*
***
*****
*******
*********
*******
*****
***
*
方法一:
我们可以将这个菱形,拆成2个三角形,正三角和倒三角,用for循环分别输出行数i,空格j的数量,"*"号的数量k
打印正三角时,当 n==9 时,只有5行,i 的取值范围 1 ~ n/2+1,空格的取值范围 n/2+1 - i,“*"号的取值范围 2*i-1
打印倒三角时,当 n==9 时,只有4行,i 的取值范围 1 ~ n/2,空格的取值范围为 i ,”*"号的取值范围 [2*(n/2+i)-1]-2*i
代码如下:
//方法一: 可以打印出菱形,但是不推荐!!!
int main19() {int n; //代表行数cin >> n;int i, j, k;//正三角for (i = 1; i <= n/2 + 1; i++) {for (j = 1; j <= n/2+1 - i; j++) {printf(" ");}for (k = 1; k <= 2 * i - 1; k++) {printf("*");}cout << endl;}//倒三角for (i = 1; i <= n/2 ; i++) {for (j = 1; j <= i; j++) {printf(" ");}for (k = 1; k <= (2*(n/2+1)-1)-2*i ; k++) {printf("*");}cout << endl;}return 0;
}方法二:采用曼哈顿距离


代码如下:
//方法二: 运用曼哈顿距离
int main() {int n;cin >> n;//构造一个 n×n 的正方形//计算每个方格到中心原点的距离//如果距离<=n/2 , 都是"*"//如果距离>n/2 , 为空格//(cx,cy)表示中心原点int cx = n / 2;int cy = n / 2;for (int i = 0; i <= n-1; i++) {for (int j = 0; j <= n-1; j++) {if (abs(i - cx) + abs(j - cy) <= n / 2) {printf("*");}else {printf(" ");}}cout << endl;}return 0;
}例题11:输入一个n,打印n阶空心菱形,n为奇数
n = 9 的结果
*
* *
* *
* *
* *
* *
* *
* *
*
空心菱形,顾名思义,和实心菱形相比,只有外围需要打印"*",内部都是空格


代码如下:
int main() {int n;cin >> n;//构造一个 n×n的正方形//计算每个方格到中心原点的距离//如果距离<=n/2 , 都是"*"//如果距离>n/2 , 为空格//(cx,cy)表示中心原点int cx = n / 2;int cy = n / 2;for (int i = 0; i <= n - 1; i++) {for (int j = 0; j <= n - 1; j++) {if (abs(i - cx) + abs(j - cy) == n / 2) {printf("*");}else {printf(" ");}}cout << endl;}return 0;
}六、习题
第1题 偶数
输出1~100之间(包括1和100)的全部偶数

代码如下:
int main() {int n;cin >> n;for (int i = 1; i <= n; i += 2) {cout << i << endl;}return 0;
}第2题 奇数
输入一个整数x,输出1到x之间(包括1和x)的全部奇数

代码如下:
int main() {int n;cin >> n;for (int i = 1; i <= n; i += 2) {cout << i << endl;}return 0;
}第3题 正数
输入6个数字,它们要么是正数,要么是负数,统计并输出正数的个数,6个数字,每个占一行,输出格式为"x positive numbers",其中x为正数的个数

代码如下:
int main() {int num = 0;double x;for (int i = 0; i <= 5; i++) {cin >> x;if (x > 0) {num++;}}cout << num << " positive numbers" << endl;return 0;
}另外,我们还可以使用数组来解决
int main() {int num = 0;int a[6];for (int i = 0; i <= 5; i++) {cin >> a[i];if (a[i] > 0) {num++;}}cout << num << " positive numbers" << endl;return 0;
}第4题 连续奇数的和1
给定2个整数x和y,输出在它们之间(不包括x和y)的所有奇数的和,第一行输入x,第二行输入y,输出一个整数,表示所有满足条件的奇数的和

代码如下:
void swap(int& a, int& b) {int temp = a;a = b;b = temp;
}int main() {int x, y;cin >> x >> y;if (x > y) swap(x, y);int sum = 0;for (int i = x + 1; i < y; i++) {if (i % 2 == 0)continue;sum += i;}cout << "所有满足条件的奇数的和为:"<<sum << endl;return 0;
}第5题 最大数和它的位置
给定100个数,请你找出其中最大的数字,以及它的输入位置(位置从1开始),输入共100行,每行包含1个整数,第一行输出最大的数字,第二行输出该数字的输入位置

我们采用擂台法解决此类问题:
int main() {int a[110];for (int i = 0; i <= 99; i++) {cin >> a[i];}int max = a[0];int max_i = 0;for (int j = 1; j <= 99; j++) {if (a[j] > max) {max = a[j];max_i = j;}}cout << "最大的数字为: " << max << endl;cout << "该数字的输入位置为: " << max_i + 1 << endl;return 0;
}还可以进一步简化:
int main() {int a[110];int max = 0; //这里max赋值为0,方便和后面的数进行比较int max_i;for (int i = 0; i <= 99; i++) {cin >> a[i];if (a[i] > max) {max = a[i];max_i = i;}}cout << "最大的数字为: " << max << endl;cout << "该数字的输入位置为: " << max_i + 1 << endl;return 0;
}第6题 递增序列

代码如下:
int main() {int x;while (true) {cin >> x;if (x == 0) break;for (int i = 1; i <= x; i++) {cout << i << " ";}cout << endl;}return 0;
}片尾
今天我们学习了C++蓝桥杯基础篇(三),希望这篇文章对友友们有所帮助!!!
求点赞收藏加关注!!!
谢谢大家!!!

相关文章:

C++蓝桥杯基础篇(三)
片头 哈喽!小伙伴们,大家好~,今天我们来学习蓝桥杯基础篇(三),继续练习相关习题,准备好了吗?我们开始啦~ 一、while循环 可以简单理解为循环版的if语句。if语句是判断1次࿰…...

微信小程序的制作
制作微信小程序的过程大致可以分为几个步骤:从环境搭建、项目创建,到开发、调试和发布。下面我会为你简要介绍每个步骤。 1. 准备工作 在开始开发微信小程序之前,你需要确保你已经完成了以下几个步骤: 注册微信小程序账号&…...

Sass更新:@import——>@use
背景:将一个公共的CSS样式文件导入到任意一个组件中进行使用 一、创建并使用CSS公共样式文件 1、在目录的assets目录下创建一个style文件夹,里面存放一个.scss文件(例:mixin.scss) 2、文件内以mixin来设置名为flex的…...
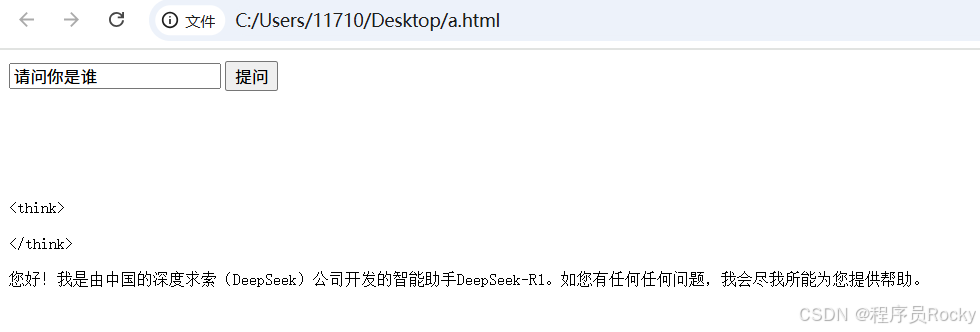
Python使用Flask结合DeepSeek开发
一、背景 我之前关于DeepSeek使用ollama部署的文章大家可以把DeepSeek大模型部署起来。那么ollama还提供了可以调用对应部署模型的API接口。我们可以基于这些接口,做自己的二次开发。使用pythonflaskollama就可以进行模型对话调用。并且前端采用SSE的技术࿰…...

python中的抽象类在项目中的实际应用
抽象类在项目中的实际应用主要体现在 规范代码结构、强制子类实现某些方法、提供部分通用功能,让代码更稳定、易维护。 举个例子:数据校验器 假设你在做一个 用户输入校验系统,需要支持 数字校验、字符串校验 和 邮箱校验。如果不用抽象类&…...
)
New Game--(单调队列)
I - New Game 有一种新的游戏,Monocarp 想要玩。这个游戏使用一副包含 n 张牌的牌堆,其中第 i 张牌上写有一个整数 a_i。 在游戏开始时,Monocarp 可以在第一轮选择牌堆中的任意一张牌。在接下来的每一轮中,Monocarp 可以选择一张…...

mapbox V3 新特性,添加下雪效果
👨⚕️ 主页: gis分享者 👨⚕️ 感谢各位大佬 点赞👍 收藏⭐ 留言📝 加关注✅! 👨⚕️ 收录于专栏:mapbox 从入门到精通 文章目录 一、🍀前言1.1 ☘️mapboxgl.Map 地图对象…...

无人机遥感在农林信息提取中的实现方法与GIS融合制图教程
遥感技术作为一种空间大数据手段,能够从多时、多维、多地等角度,获取大量的农情数据。数据具有面状、实时、非接触、无伤检测等显著优势,是智慧农业必须采用的重要技术之一。 一:综合态势分析 1.1 研究区及作物品种分析 ÿ…...
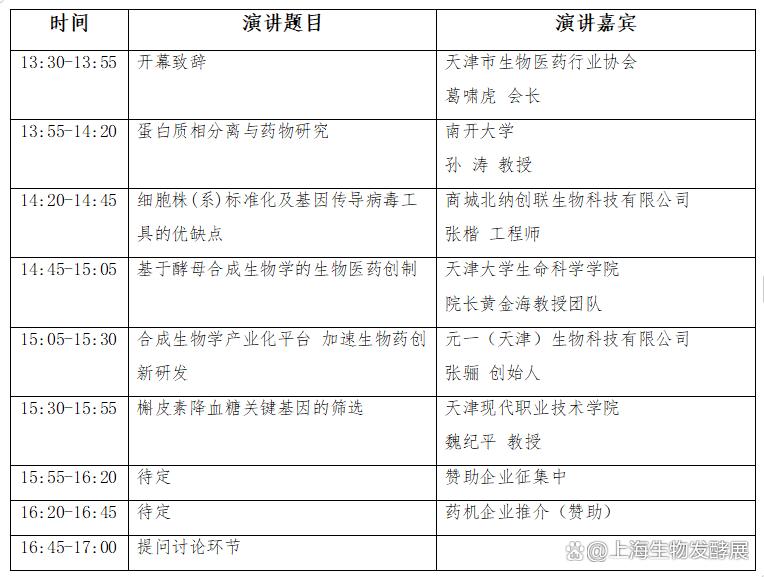
生物发酵展与2025生物医药创新技术与应用发展论坛同期盛大举办
近日,备受瞩目的生物发酵展与2025生物医药创新技术与应用发展论坛暨展览会宣布将同期盛大举办。这一消息标志着生物科技领域两大盛会的强强联合,将为全球生物科技与医药行业带来前所未有的交流与合作机遇。 生物发酵展作为生物科技领域的知名展会&#x…...

Jenkins 配置 Git Repository 五
Jenkins 配置 Git Repository 五 这里包含了 Freestyle project 任务类型 和 Pipeline 任务类型 关于 Git 仓库的配置,如下 不同的任务类型,只是在不同的模块找到 配置 Git 仓库 找到 Git 仓库配置位置之后,所有的任务类型配置都是一样的 …...

记录阿里云CDN配置
网站接入CDN全流程,共4步!-阿里云开发者社区 1、开通阿里云CDN服务 2、添加加速域名 3、验证域名归属权 4、域名添加CDN生成的CNAME解析 按照官网描述增加。细节点: 1. 域名和泛域名区别 2.开启https,要用nginx的证书,和项…...

mapbox 从入门到精通 - 目录
👨⚕️ 主页: gis分享者 👨⚕️ 感谢各位大佬 点赞👍 收藏⭐ 留言📝 加关注✅! 👨⚕️ 收录于专栏:mapbox 从入门到精通 文章目录 一、🍀总目录1.1 ☘️ mapbox基础1.2 ☘️…...

mysql中general_log日志详解
介绍 1.记录范围:这个log里面会记录MySQL所有的SQL语句,不管是查询语句,还是DML语句,还是DDL语句,还是DCL语句,这些语句统统都会被记录在general log文件中。就连我们连接和断开MySQL数据库的这些语句。 2…...

算法与数据结构:从基础到深入
1. 数组 (Array) 定义 一组连续内存空间存储的相同类型元素的集合。特点:通过下标(索引)快速访问元素,但大小固定(静态数组)或可扩展(动态数组)。 核心操作 操作时间复杂度说明访…...

基于千兆5G网关的5G急救车方案
伴随5G网络的全面建成,5G技术的低延时、高速率、广接入等优势,为各行各业都带来了新一轮技术升级。在医疗救援方面,救护车是链接病患与医院的重要纽带,得益于5G物联网的融合应用,救护车也快速向联网化、信息化、智能化…...

【C#】的WPF或是WinForm实现Ctrl+ 的快捷键组合使用
在C#中,无论是WPF还是WinForms应用程序,处理快捷键(例如 Ctrl )通常涉及检测键盘输入并执行相应的命令或方法。 WPF 实现 在WPF中,可以通过设置一个控件的 InputBindings 属性来绑定快捷键。 <Window x:Class&qu…...

c语言样式主题 清爽风格 代码色彩 keil风格 适合单片机开发GD32 STM32等 cursor或者vscode 的settings.json文件
c语言样式主题 清爽风格 代码色彩 keil风格 适合单片机开发GD32 STM32等 cursor或者vscode 的settings.json文件 如上图,是不是和keil mdk很相近。 代码色彩,简单,配合 // 设置工作台主题为 Visual Studio 2017 Light - C 主题使用…...

DeepSeek API 调用 - Spring Boot 实现
DeepSeek API 调用 - Spring Boot 实现 1. 项目依赖 在 pom.xml 中添加以下依赖: <dependencies><dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-webflux</artifactId></depe…...
)
图数据库Neo4j面试内容整理-节点(Node)
在图数据库中,节点(Node)是图结构中的基本构建块,代表实体或对象。节点通常用于存储数据模型中的主要对象,比如人、商品、地点等。在图数据库中,节点是通过标签(Label)来分类的,并且可以包含属性(Property)来描述它们的详细信息。 1. 节点的组成<...

使用verilog 实现 cordic 算法 ----- 旋转模式
1-设计流程 ● 了解cordic 算法原理,公式,模式,伸缩因子,旋转方向等,推荐以下链接视频了解 cordic 算法。哔哩哔哩-cordic算法原理讲解 ● 用matlab 或者 c 实现一遍算法 ● 在FPGA中用 verilog 实现,注意…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...
