SpringBoot Bug 日志
Spring 循环依赖问题
Bug如下

wxMpConfiguration → subscribeHandler → wxMsgServiceImpl → wxMpConfiguration
解决方案
| 方案 | 实施方式 | 注意事项 |
|---|---|---|
| 接口抽象 | 定义 WxMpService 接口,通过接口注入 | 最佳设计实践 |
| Setter 注入 | 对非必要依赖使用 setter 方法 | 降低耦合度 |
| @Lazy 注解 | 在循环点添加延迟加载 | 需测试性能影响 |
| 配置允许循环 | spring.main.allow-circular-references=true | 临时解决方案 |
tips:该模式常见于三方 SDK 集成场景,建议通过模块化隔离微信相关功能
典型循环依赖模式配置类 → 处理器 → 服务实现 → 配置类
延迟初始化
# application.properties
spring.main.lazy-initialization=true
允许循环依赖(临时方案)
Properties
# application.properties
spring.main.allow-circular-references=true
解决办法
为了方便 同上(延迟初始化)
使用@lazy注解在WxMpService的自动注入处
@Lazy@Autowiredprivate WxMpService wxMpService;
相关文章:

SpringBoot Bug 日志
Spring 循环依赖问题 Bug如下 wxMpConfiguration → subscribeHandler → wxMsgServiceImpl → wxMpConfiguration 解决方案 方案实施方式注意事项接口抽象定义 WxMpService 接口,通过接口注入最佳设计实践 Setter 注入对非必要依赖使用 setter 方法降低耦合度 L…...

halo发布文章的插件问题分析
前言 在准备发文到 halo 系统的时候提示错误如下,全是乱码 尝试将 halo 插件卸载后,再将插件目录下的文件全部删除 插件目录在 C:\Users\Administrator\.vscode\extensions\halo-dev.halo-1.3.0 然后再重新安装插件,在进行初始化的时候依然…...

2.5 模块化迁移策略:从传统项目到模块化系统
模块化迁移策略:从传统项目到模块化系统 将传统 Java 项目迁移至 JDK 9 模块化系统是一项系统性工程,需分阶段实施以降低风险。以下是详细的迁移策略、工具使用和实战示例。 1. 迁移阶段划分 阶段目标关键操作阶段1:兼容性验证确保项目能在…...

java商城解决方案
数字化时代,电子商务已成为企业拓展市场的重要渠道。对于想要建立在线商店的企业来说,选择正确的技术堆栈至关重要。 Java作为一种成熟且广泛使用的编程语言,为构建购物中心提供了强大的功能和灵活性。 商城Java源码:商城开发的核…...

算法-哈希表篇05-四数相加II
四数相加II 力扣题目链接 题目描述 给你四个整数数组 nums1、nums2、nums3 和 nums4 ,数组长度都是 n ,请你计算有多少个元组 (i, j, k, l) 能满足: 0 < i, j, k, l < n nums1[i] nums2[j] nums3[k] nums4[l] 0 解题思路 把数…...

WPS或word接入智能AI
DeepSeek接入WPS 配置WPS (1)下载 OfficeAl助手插件: 插件下载地址:https://www.office-ai.cn/。 安装插件后,打开WPS,菜单栏会新增"OfficeAl助手”选项卡。 如果没有出现, 左上找到文件菜单 -> 选项 ,在…...

Leetcode:学习记录
一、滑动窗口 1. 找出数组中元素和大于给定值的子数组的最小长度 右指针从左到右遍历,在每个右指针下,如果去掉左边元素的元素和大于等于给定值则左指针右移一次,直到小于给定值,右指针右移一个。 2.找到乘积小于给定值的子数组…...
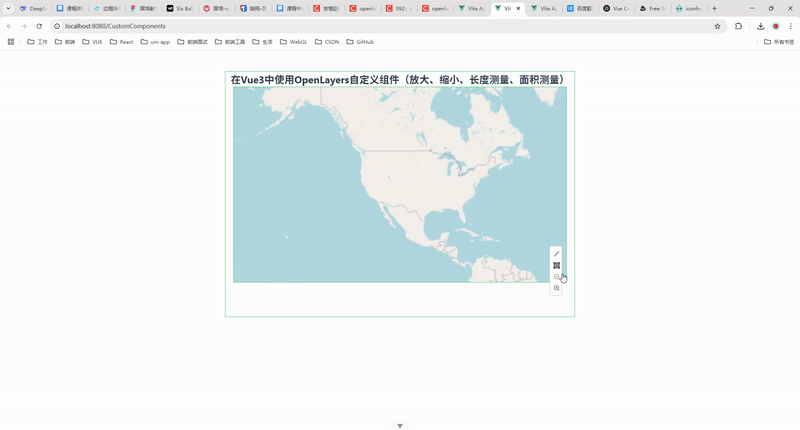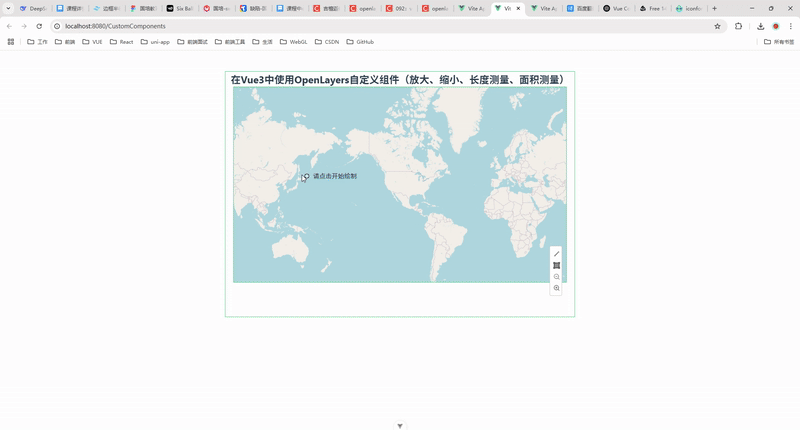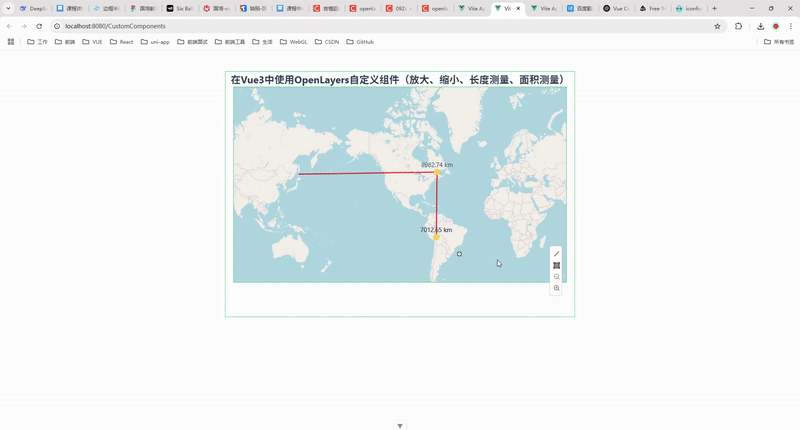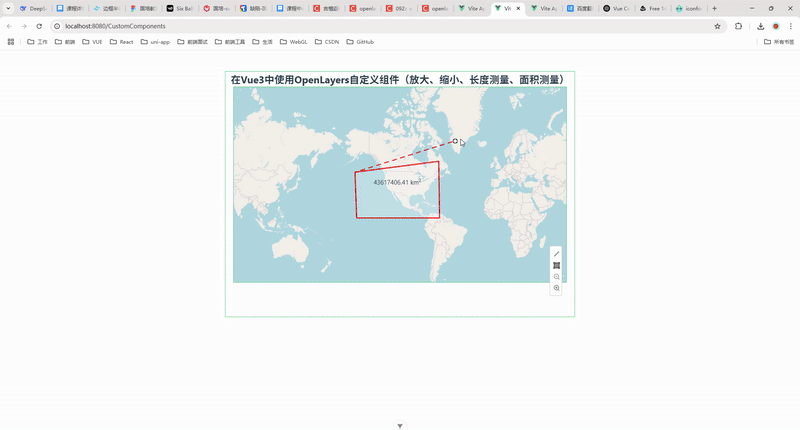
86.在 Vue 3 中使用 OpenLayers 自定义组件(放大、缩小、长度测量、面积测量)
摘要 在 WebGIS 开发中,OpenLayers 是一个非常强大的开源地图库,它可以在 Web 应用中渲染高效的地图。本篇文章将介绍如何在 Vue 3 中使用 OpenLayers,并封装一个自定义地图控件组件,实现地图的放大、缩小、长度测量和面积测量功能…...

http 与 https 的区别?
HTTP(超文本传输协议)和 HTTPS(安全超文本传输协议)是互联网通信的基础协议。随着网络技术的发展和安全需求的提升,HTTPS变得越来越重要。本文将深入探讨HTTP与HTTPS之间的区别,包括其工作原理、安全性、性能、应用场景及未来发展等。 1. HTTP与HTTPS的基本概念 1.1 HT…...

SAIL-RK3576单板运行7b的deepseek对话模型
大概流程: 使用ollama工具进行deepseek的模型部署和使用,先安装ollama工具,在使用ollama工具拉去deepseek模型,最后使用ollama工具加载deepseek模型进行对话...

独立C++ asio库实现的UDP Server
以下是一个使用独立的 C Asio 库实现的 UDP 服务器的示例代码。这个 UDP 服务器可以监听指定端口,接收客户端发送的数据,并将接收到的数据原样返回给客户端。 #include <iostream> #include <asio.hpp> #include <array>class UdpSer…...

SQL Server STUFF 函数的用法及应用场景
在 SQL Server 中,STUFF 函数是一种强大的字符串处理工具,常用于删除指定位置的字符并插入新的字符。通过这个函数,开发者能够灵活地修改字符串,从而在数据处理、字符串拼接和格式化等方面大显身手。本文将深入探讨 STUFF 函数的语…...

MongoDB进阶篇-索引
文章目录 1. 索引概述 2. 索引的类型 2.1 单字段索引 2.2 复合索引 2.3 其他索引 2.3.1 地理空间索引(Geospatial Index) 2.3.2 文本索引(Text Indexes) 2.3.3 哈希索引(Hashed Indexes) 3. 索引相关操作 3.1 查看索引 3.2 创建索引 3.3.1 创建单字段索引 3.3.2 创建复合…...

《机器学习数学基础》补充资料:柯西—施瓦茨不等式以及相关证明
《机器学习数学基础》 153 页,针对图 3-4-3,提出了一个问题:“点 A A A 到 W \mathbb{W} W 上的一个点的距离有无穷多个。现在,我们最关心的是其中最短的那个,怎么找?请参阅 3.6 节。”并且,在…...

VisionPro 划痕检测小练习
划痕检测,我这里用到的是Sobel算子和blob斑点匹配以及blob里面的形态学调整 Sobel 是一种在数字图像处理和计算机视觉领域广泛应用的算法,主要用于边缘检测 脚本展示 #region namespace imports using System; using System.Collections; using System.Drawing; …...

解析 2025 工业边缘计算:三大技术风向的影响力
工业数字化转型的加速,工业边缘计算市场正呈现出蓬勃发展的态势。展望 2025 年,以下三大技术将成为引领工业边缘计算发展的重要风向标。 其一,人工智能与边缘计算的深度融合。人工智能技术将更广泛地应用于工业边缘设备,实现更智…...

企语企业管理系iFair(F23.2_a0)在Debian操作系统中的安装
起因:在安装了F24.8版本后,发现生产用环境和测试、开发用环境还是分开的好。 旧版的用来实验、测试,新版的一步一步小心的配置、使用是比较稳妥的操作。因此,决定在KVM虚拟机上搭建一个F23.2版本的企语系统。 一、 存在的问题 而…...

如何在Flask中处理静态文件
哈喽,大家好,我是木头左! 本文将详细介绍如何在Flask中处理静态文件,包括如何配置静态文件夹、如何访问静态文件以及如何处理静态文件的缓存问题。 配置静态文件夹 在Flask中,你可以通过static_folder参数来指定静态文件夹。默认情况下,Flask会在项目的根目录下寻找名为…...

无人机飞行试验大纲
无人机飞行试验大纲 编制日期:2025年02月11日 一、试验目的与背景 本次无人机飞行试验旨在验证无人机的飞行性能、控制系统稳定性、机体结构强度以及各项任务执行能力。随着无人机技术在各个领域的广泛应用,对其性能进行全面、系统的测试显得…...

C语言初阶牛客网刷题——JZ65 不用加减乘除做加法】【难度:简单】
1. 题目描述 牛客网OJ题链接 写一个函数,求两个整数之和,要求在函数体内不得使用、-、*、/四则运算符号。 2. 分析 十进制相加思想: 157 , 先计算不考虑进位的相加结果 12 (因为 57 的不考虑进位的结果是 2 &#x…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...

windows系统MySQL安装文档
概览:本文讨论了MySQL的安装、使用过程中涉及的解压、配置、初始化、注册服务、启动、修改密码、登录、退出以及卸载等相关内容,为学习者提供全面的操作指导。关键要点包括: 解压 :下载完成后解压压缩包,得到MySQL 8.…...

「全栈技术解析」推客小程序系统开发:从架构设计到裂变增长的完整解决方案
在移动互联网营销竞争白热化的当下,推客小程序系统凭借其裂变传播、精准营销等特性,成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径,助力开发者打造具有市场竞争力的营销工具。 一、系统核心功能架构&…...

stm32wle5 lpuart DMA数据不接收
配置波特率9600时,需要使用外部低速晶振...
