基于Python的Optimal Interpolation (OI) 方法实现
前言
Optimal Interpolation (OI) 方法概述与实现
Optimal Interpolation (OI) 是一种广泛应用于气象学、海洋学等领域的空间数据插值方法。该方法通过结合观测数据与模型预测数据,最小化误差方差,从而实现对空间数据的最优插值。以下是OI方法的一般步骤和实现:
- 定义背景场与观测数据
在OI中,背景场(通常是模型预测值)和观测值是两个主要的数据源。设:
y:观测值(如测量数据)
b:背景场(如数值天气预报模型的预测数据)
R:观测误差协方差矩阵
B:背景误差协方差矩阵
通过加权平均的方式,OI结合了背景场与观测数据,计算出最优的插值结果。
-
加权平均与最优估计
插值结果通过加权平均获得,权重由误差协方差矩阵和增益矩阵(K)确定。增益矩阵决定了背景场与观测数据对最终估计结果的影响权重。通过计算增益矩阵,OI方法最小化了预测误差,结合了两种数据源的优势。 -
误差分析与性能评估
OI方法的性能依赖于误差协方差矩阵的精确度。准确的误差协方差矩阵估计对于插值的可靠性至关重要。插值后的误差分析可以帮助评估加权平均的精度,确保OI方法的正确性。 -
空间映射与协方差矩阵设计
在某些情况下,背景场与观测场的空间位置不一致,需要进行空间映射。此时,需要设计矩阵H,用于将背景场数据与观测数据对齐。
OI 方法实现:
以下代码实现了OI方法,结合了多个背景场数据和观测数据,通过加权平均计算最优插值结果。代码详细注释了每一步的具体实现。
二、使用步骤
1.引入库
import xarray as xr
import matplotlib.pyplot as plt
import numpy as np
from scipy.spatial.distance import cdist# 1. 加载多个背景场数据
# 假设背景场数据存储在多个NetCDF文件中,每个文件包含一个时间步的温度数据
nc_files = ['background_data_1.nc', 'background_data_2.nc', 'background_data_3.nc']# 加载多个背景场数据并合并为一个列表
background_data_list = []
for nc_file in nc_files:ds = xr.open_dataset(nc_file) # 打开NetCDF文件background_data = ds['temperature'].sel(time=0) # 选择时间步为0的数据background_data_list.append(background_data)# 假设所有背景场数据的经纬度网格一致,提取经纬度信息
lat = ds['lat'].values
lon = ds['lon'].values
grid_lon, grid_lat = np.meshgrid(lon, lat)# 将多个背景场数据转化为numpy数组
background_data_array = np.array([data.values for data in background_data_list])# 2. 观测数据(点数据)
# 假设观测数据包含经纬度和观测值(温度),格式为 [经度, 纬度, 温度]
observations = np.array([[103.5, 30.5, 15.2], # (lon, lat, temperature)[104.0, 31.0, 16.7],[105.0, 32.0, 14.6]
])# 3. 计算背景网格点与观测点的距离
# 创建背景网格点坐标的二维数组
grid_points = np.column_stack([grid_lon.ravel(), grid_lat.ravel()])
# 提取观测数据的经纬度部分
obs_points = observations[:, :2]# 计算背景网格点与观测点之间的欧氏距离
distances = cdist(grid_points, obs_points)# 4. 为每个背景点计算权重(基于距离)
# 距离越近,权重越大,因此使用指数函数来计算权重
weights = np.exp(-distances) # 基于欧氏距离计算权重# 归一化权重,使其总和为1
weights_sum = np.sum(weights, axis=1, keepdims=True)
normalized_weights = weights / weights_sum # 归一化处理# 5. 使用OI方法计算栅格插值结果
# 对于多个背景场数据,计算加权平均值
# OI估计值 = Σ (每个背景场的权重 * 背景场的值)
oi_result = np.sum(normalized_weights * background_data_array.T, axis=1).reshape(background_data_list[0].shape)# 6. 可视化OI结果
# 使用Matplotlib展示OI结果
plt.imshow(oi_result, cmap='viridis', interpolation='nearest')
plt.colorbar(label='Temperature') # 添加颜色条,表示温度范围
plt.title('Optimal Interpolation with Multiple Background Fields') # 图表标题
plt.show()# 7. 保存OI结果为新的NetCDF文件(如果需要)
# 将OI结果保存为NetCDF格式,以便后续使用
oi_ds = xr.Dataset({'temperature': (['lat', 'lon'], oi_result)}, # 创建新的Datasetcoords={'lat': lat, 'lon': lon} # 设置经纬度坐标
)# 保存为NetCDF文件
oi_ds.to_netcdf('oi_result_multiple_backgrounds.nc')总结

加载背景场数据:
使用xarray加载多个NetCDF文件中的背景场数据,每个文件对应一个背景场。
提取背景场的温度数据,并保存为列表。
观测数据:
假设观测数据是一个包含经纬度和温度值的数组,其中每一行代表一个观测点的经纬度和观测值。
计算背景网格点与观测点的距离:
使用scipy.spatial.distance.cdist计算背景网格点与观测点之间的欧氏距离。
计算加权平均:
基于距离计算每个背景场的权重,距离越近,权重越大。然后通过归一化使权重之和为1。
计算OI插值结果:
对多个背景场数据进行加权平均,得到最终的插值结果。
可视化:
使用matplotlib展示OI插值结果,生成温度分布图,并添加颜色条。
保存结果:
使用xarray将OI插值结果保存为NetCDF文件,便于后续分析和存储。
相关文章:

基于Python的Optimal Interpolation (OI) 方法实现
前言 Optimal Interpolation (OI) 方法概述与实现 Optimal Interpolation (OI) 是一种广泛应用于气象学、海洋学等领域的空间数据插值方法。该方法通过结合观测数据与模型预测数据,最小化误差方差,从而实现对空间数据的最优插值。以下是OI方法的一般步骤…...

初学 mybatis
前言 回顾之前 不使用 mybatis 框架,我们是怎么通过Java 操作数据库的 "jdbc" 前提:使用maven 构建的项目 1 添加 关于jdbc 的依赖,以及辅助操作数据库的 commons-dubli jar包 截取 前后端项目 2 添加配置文件里面内容有&…...

机器学习:k均值
所有代码和文档均在golitter/Decoding-ML-Top10: 使用 Python 优雅地实现机器学习十大经典算法。 (github.com),欢迎查看。 在“无监督学习”中,训练样本的标记信息是未知的,目标是通过对无标记训练样本的学习来揭示数据的内在性质及规律&…...

保姆级GitHub大文件(100mb-2gb)上传教程
GLF(Git Large File Storage)安装使用 使用GitHub desktop上传大于100mb的文件时报错 The following files are over 100MB. lf you commit these files, you will no longer beable to push this repository to GitHub.com.term.rarWe recommend you a…...

1.【BUUCTF】[SUCTF 2019]EasyWeb
进入题目页面如下 给出源码开始代码审计 <?php // 定义一个名为 get_the_flag 的函数,该函数主要处理文件上传逻辑 function get_the_flag(){// 构造用户上传文件的目录,目录名是 "upload/tmp_" 加上客户端 IP 地址的 MD5 哈希值$userdir…...
二级索引)
CloudberryDB(七)二级索引
在CloudberryDB中,二级索引的概念与PostgreSQL中的类似。但是,由于分布式特性,创建和使用二级索引需要考虑一些额外的因素。以下是关于二级索引的一些要点: 1. **创建索引**:在Greenplum中,可以使用CREATE…...

P1878 舞蹈课(详解)c++
题目链接:P1878 舞蹈课 - 洛谷 | 计算机科学教育新生态 1.题目解析 1:我们可以发现任意两个相邻的都是异性,所以他们的舞蹈技术差值我们都要考虑,4和2的差值是2,2和4的差值是2,4和3的差值是1,根…...

何须付费免费它不香吗
聊一聊 又是一年开学季。 开学了发一些应时期的小软件。 今天给大家分享一款学校班级课程表工具。 这款工具可以投放在学校电子大屏上。 支持学校的白板软件。 软件介绍 学校班级课程表 工具界面清爽,信息能一目了然。 虽然看感觉功能简单,但每个…...

ELK组成及实现原理
ELK是由三个主要组件组成的日志处理和搜索平台,分别是: Elasticsearch:Elasticsearch 是一个基于Lucene构建的开源搜索引擎,提供强大的搜索、分析功能。它负责存储和索引所有数据,并提供实时搜索能力。数据可以通过HTT…...

【Vue3源码解析】响应式原理
源码环境搭建 【Vue3源码解析】应用实例创建及页面渲染-CSDN博客 写文章时的Vue 版本: "version": "3.5.13",针对单个包进行开发环境打包、测试。 pnpm run dev reactivityreactive 创建响应式对象 packages/reactivity/src/reactive.ts …...

servlet中的ServletContext
设置、获取ServletContext配置信息 与ServletConfig不同的是,所有Servlet共享一份ServletContext 在web.xml中设置配置信息 <?xml version"1.0" encoding"UTF-8"?> <web-app xmlns"https://jakarta.ee/xml/ns/jakartaee"x…...

第1825天 | 我的创作纪念日:缘起、成长经历、大方向
目录 缘起一、成为创作者的初心(一)好记性不如烂笔头(二)文档可以帮助多个人解决同一个问题(三)加深自己对问题的理解,对技术的研究 二、实战项目中的经验分享(一)项目背…...

如何在 Mac 上解决 Qt Creator 安装后应用程序无法找到的问题
在安装Qt时,遇到了一些问题,尤其是在Mac上安装Qt后,发现Qt Creator没有出现在应用程序中。通过一些搜索和操作,最终解决了问题。以下是详细的记录和解决方法。 1. 安装Qt后未显示Qt Creator 安装完成Qt后,启动应用程…...

Java 设计模式之迭代器模式
文章目录 Java 设计模式之迭代器模式概述UML代码实现Java的迭代器 Java 设计模式之迭代器模式 概述 迭代器模式(Iterator),提供一种方法顺序访问一个聚合对象中的各个元素,而又不暴露该对象的内部表示。 UML Iterator:迭代器接口ÿ…...
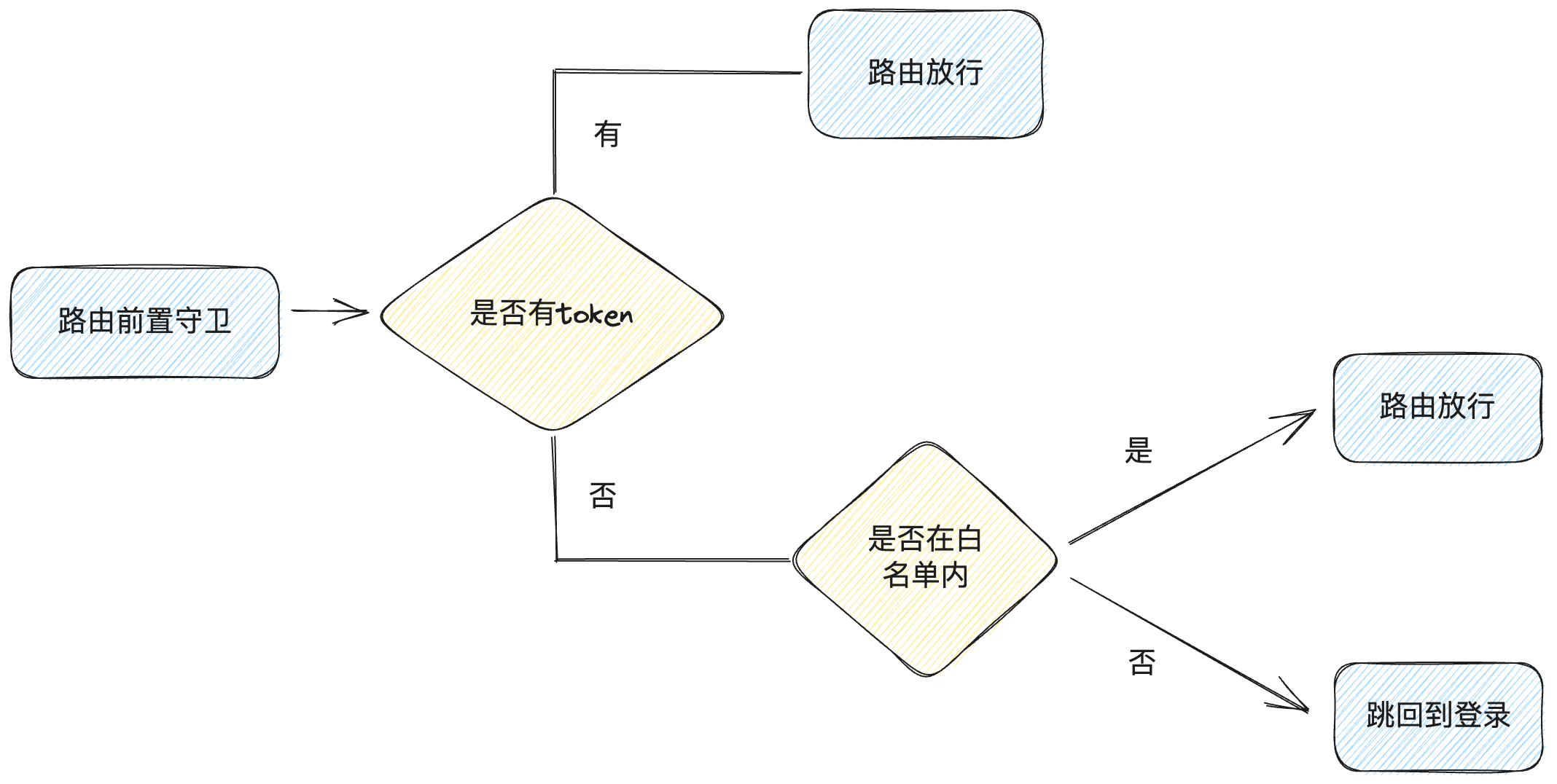
登录演示和功能拆解
登录演示和功能拆解 表单基础校验实现 1. 基础双向绑定 <template><el-form><el-form-item label"账号"><el-input v-model"formData.username" /></el-form-item><el-form-item label"密码"><el-inpu…...

DeepSeek深度求索API多线程批量写原创文章软件-ai痕迹极低
DeepSeek是一款由国内人工智能公司研发的大型语言模型,拥有强大的自然语言处理能力,能够理解并回答问题,还能辅助写代码、整理资料和解决复杂的数学问题。 与OpenAI开发的ChatGPT相比,DeepSeek不仅率先实现了媲美OpenAI-o1模型的…...

Redis进阶使用
在日常工作中,使用Redis有什么需要注意的? 设置合适的过期时间。尽量避免大key问题,避免用字符串存储过大的数据;避免集合的数据量太大,要定期清除。 常用的数据结构有哪些?用在什么地方? 按…...

Python常见面试题的详解6
1. 按字典 value 值排序 要点:对于给定字典,使用 sorted() 函数结合 items() 方法,依据 value 进行排序,也可以定义一个通用函数,支持按 value 升序或降序排序。示例: python d {a: 1, b: 2, c: 3, d: …...

Linux基础之文件权限的八进制表示法
1. Linux 文件权限概述 在 Linux 中,每个文件或目录都有三种基本权限,分别是: 读权限 - r:允许查看文件内容。写权限 - w:允许修改文件内容。执行权限 - x:允许执行文件或进入目录。 每个文件或目录的权…...

数据结构与算法面试专题——堆排序
完全二叉树 完全二叉树中如果每棵子树的最大值都在顶部就是大根堆 完全二叉树中如果每棵子树的最小值都在顶部就是小根堆 设计目标:完全二叉树的设计目标是高效地利用存储空间,同时便于进行层次遍历和数组存储。它的结构使得每个节点的子节点都可以通过简…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...
