[数据结构]红黑树,详细图解插入
目录
一、红黑树的概念
二、红黑树的性质
三、红黑树节点的定义
四、红黑树的插入(步骤)
1.为什么新插入的节点必须给红色?
2、插入红色节点后,判定红黑树性质是否被破坏
五、插入出现连续红节点情况分析+图解(看uncle节点)
5.1、uncle存在且为红
5.2、uncle不存在
1、单旋
2、双旋
5.3、uncle存在且为黑
1、单旋
2、双旋
六、插入总结
1、红黑树插入的两种步骤
2、插入代码
七、红黑树总结及代码
一、红黑树的概念
红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色,可以是Red或 Black。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制,
红黑树确保——没有一条路径会比其他路径长出两倍,因而是接近平衡的

二、红黑树的性质
1. 每个结点不是红色就是黑色
2. 根节点是黑色的
3. 如果一个节点是红色的,则它的两个孩子结点是黑色的 (没有连续的红节点)
4. 从任一结点到其所有后代叶结点的简单路径上,均包含相同数目的黑结点
5. 每个叶子结点都是黑色的(此处的叶子结点指的是NIL空结点)
最优情况:全黑或每条路径都是一黑一红的满二叉树,高度logN
最差情况:每颗子树左子树全黑,右子树一黑一红。高度2*logN。
可以发现,最坏情况的时间复杂度和AVL树一样,都是O(logN),但是红黑树这种近似平衡的结构减少了大量旋转,综合性能优于AVL树。
三、红黑树节点的定义
enum Colour
{RED,BLACK
};template<class K, class V>
struct RBTreeNode
{RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;pair<K, V> _kv;Colour _col;RBTreeNode(const pair<K, V>& kv):_left(nullptr), _right(nullptr), _parent(nullptr), _kv(kv), _col(RED){}
};四、红黑树的插入(步骤)
1.为什么新插入的节点必须给红色?
(1)新节点给红色,可能出现连续红节点
(2)如果新节点给黑色,必定会违反性质4(其每条路径的黑色节点数量相同)
2、插入红色节点后,判定红黑树性质是否被破坏
因为新节点的默认颜色是红色,所以
(1)双亲节点的颜色是黑色,没有违反红黑树任何 性质,则不需要调整;
(2)双亲节点为红色,就会出现连续的红节点,此时需要对红黑树分情况来讨论:见下一部分
五、插入出现连续红节点情况分析+图解(看uncle节点)
约定:cur为当前节点,p为父节点,g为祖父节点,u为叔叔节点
下面的分析都是以p为g的左孩子为例
5.1、uncle存在且为红

cur插入后,p和u变黑,g变红
(1)g没有父亲,g为根,g变黑
(2)g有父亲。其为黑,结束;其为红,后把g当成cur,继续向上调整
5.2、uncle不存在
u不存在,则cur一定是新插入的节点。
(如果cur不是新插入的节点,则cur和p一定有一个节点是黑色,否则每条路径黑色节点不相同)
下图为解释:

1、单旋

右单旋
2、双旋

左单旋 + 右单旋
5.3、uncle存在且为黑
uncle存在且为黑,是情况一变来的,所以cur原来的节点一定是黑色的。
现在其是红色的原因是,cur的子树在调整过程中将cur的颜色由黑变红。
1、单旋

右单旋
2、双旋

左单旋 + 右单旋
六、插入总结
1、红黑树插入的两种步骤
1、uncle存在且为红
2、uncle不存在 或者 uncle存在且为黑
通过分析,
uncle不存在的单旋 和 uncle存在且为黑的单旋 可以写在一起,
uncle不存在的双旋 和 uncle存在且为黑的双旋 可以写在一起,
不论uncle存在或者不存在,都不影响此步的单旋或者双旋。
当p为g的右孩子时,操作都相反。
详细步骤见其中while (parent && parent->_col == RED)这一步。
2、插入代码
bool Insert(const pair<K, V>& kv)
{if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv);cur->_col = RED;if (parent->_kv.first < kv.first){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;while (parent && parent->_col == RED){Node* grandfather = parent->_parent;//p为g左孩子if (parent == grandfather->_left){Node* uncle = grandfather->_right;// 情况1:u存在且为红 if (uncle && uncle->_col == RED){// 变色parent->_col = uncle->_col = BLACK;grandfather->_col = RED;// 继续向上处理cur = grandfather;parent = cur->_parent;}else // u不存在 或 存在且为黑{//情况2.1 , 3.1if (cur == parent->_left){// g// p// cRotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else//情况2.2 , 3.2{// g// p// cRotateL(parent);RotateR(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}//p为g右孩子else // parent == grandfather->_right{Node* uncle = grandfather->_left;// u存在且为红if (uncle && uncle->_col == RED){// 变色parent->_col = uncle->_col = BLACK;grandfather->_col = RED;// 继续向上处理cur = grandfather;parent = cur->_parent;}else{if (cur == parent->_right){// g// p// cRotateL(grandfather);grandfather->_col = RED;parent->_col = BLACK;}else{// g// p// cRotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}}_root->_col = BLACK;return true;
}七、红黑树总结及代码
红黑树和AVL树都是高效的平衡二叉树,增删改查的时间复杂度都是O(logN),红黑树不追求绝对平衡,只需保证最长路径不超过最短路径的2倍,相对而言,降低了插入和旋转的次数, 所以在经常进行增删的结构中性能比AVL树更优,而且红黑树实现比较简单,所以实际运用中红黑树更多。
using namespace std;enum Colour
{RED,BLACK
};template<class K, class V>
struct RBTreeNode
{RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;pair<K, V> _kv;Colour _col;RBTreeNode(const pair<K, V>& kv):_left(nullptr), _right(nullptr), _parent(nullptr), _kv(kv), _col(RED){}};template<class K, class V>
struct RBTree
{typedef RBTreeNode<K, V> Node;
public:bool Insert(const pair<K, V>& kv){if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv);cur->_col = RED;if (parent->_kv.first < kv.first){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;while (parent && parent->_col == RED){Node* grandfather = parent->_parent;//p为g左孩子if (parent == grandfather->_left){Node* uncle = grandfather->_right;// 情况1:u存在且为红 if (uncle && uncle->_col == RED){// 变色parent->_col = uncle->_col = BLACK;grandfather->_col = RED;// 继续向上处理cur = grandfather;parent = cur->_parent;}else // u不存在 或 存在且为黑{//情况2.1 , 3.1if (cur == parent->_left){// g// p// cRotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else//情况2.2 , 3.2{// g// p// cRotateL(parent);RotateR(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}//p为g右孩子else // parent == grandfather->_right{Node* uncle = grandfather->_left;// u存在且为红if (uncle && uncle->_col == RED){// 变色parent->_col = uncle->_col = BLACK;grandfather->_col = RED;// 继续向上处理cur = grandfather;parent = cur->_parent;}else{if (cur == parent->_right){// g// p// cRotateL(grandfather);grandfather->_col = RED;parent->_col = BLACK;}else{// g// p// cRotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}}_root->_col = BLACK;return true;}void RotateL(Node* parent){++_rotateCount;Node* cur = parent->_right;Node* curleft = cur->_left;parent->_right = curleft;if (curleft){curleft->_parent = parent;}cur->_left = parent;Node* ppnode = parent->_parent;parent->_parent = cur;if (parent == _root){_root = cur;cur->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = cur;}else{ppnode->_right = cur;}cur->_parent = ppnode;}}void RotateR(Node* parent){++_rotateCount;Node* cur = parent->_left;Node* curright = cur->_right;parent->_left = curright;if (curright)curright->_parent = parent;Node* ppnode = parent->_parent;cur->_right = parent;parent->_parent = cur;if (ppnode == nullptr){_root = cur;cur->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = cur;}else{ppnode->_right = cur;}cur->_parent = ppnode;}}bool CheckColour(Node* root, int blacknum, int benchmark){if (root == nullptr){if (blacknum != benchmark)return false;return true;}if (root->_col == BLACK){++blacknum;}if (root->_col == RED && root->_parent && root->_parent->_col == RED){cout << root->_kv.first << "出现连续红色节点" << endl;return false;}return CheckColour(root->_left, blacknum, benchmark)&& CheckColour(root->_right, blacknum, benchmark);}bool IsBalance(){return IsBalance(_root);}bool IsBalance(Node* root){if (root == nullptr)return true;if (root->_col != BLACK){return false;}// 基准值int benchmark = 0;Node* cur = _root;while (cur){if (cur->_col == BLACK)++benchmark;cur = cur->_left;}return CheckColour(root, 0, benchmark);}int Height(){return Height(_root);}int Height(Node* root){if (root == nullptr)return 0;int leftHeight = Height(root->_left);int rightHeight = Height(root->_right);return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;}private:Node* _root = nullptr;public:int _rotateCount = 0;
};相关文章:

[数据结构]红黑树,详细图解插入
目录 一、红黑树的概念 二、红黑树的性质 三、红黑树节点的定义 四、红黑树的插入(步骤) 1.为什么新插入的节点必须给红色? 2、插入红色节点后,判定红黑树性质是否被破坏 五、插入出现连续红节点情况分析图解(看…...

【机器学习】超参数调优指南:交叉验证,网格搜索,混淆矩阵——基于鸢尾花与数字识别案例的深度解析
一、前言:为何要学交叉验证与网格搜索? 大家好!在机器学习的道路上,我们经常面临一个难题:模型调参。比如在 KNN 算法中,选择多少个邻居(n_neighbors)直接影响预测效果。 • 蛮力猜…...

Burp Suite基本使用(web安全)
工具介绍 在网络安全的领域,你是否听说过抓包,挖掘漏洞等一系列的词汇,这篇文章将带你了解漏洞挖掘的热门工具——Burp Suite的使用。 Burp Suite是一款由PortSwigger Web Security公司开发的集成化Web应用安全检测工具,它主要用于…...
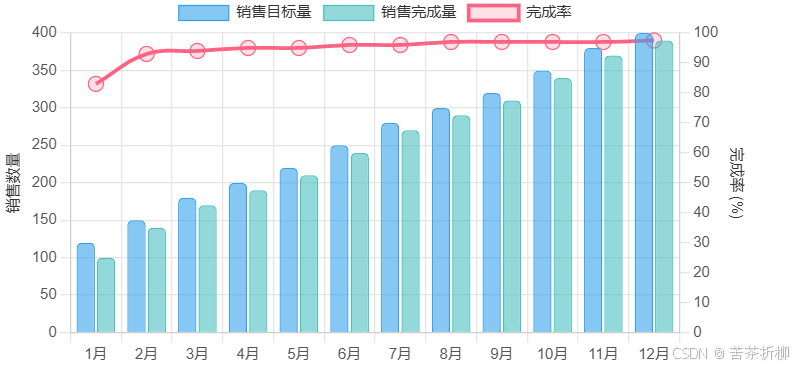
React实现自定义图表(线状+柱状)
要使用 React 绘制一个结合线状图和柱状图的图表,你可以使用 react-chartjs-2 库,它是基于 Chart.js 的 React 封装。以下是一个示例代码,展示如何实现这个需求: 1. 安装依赖 首先,你需要安装 react-chartjs-2 和 ch…...

从低清到4K的魔法:FlashVideo突破高分辨率视频生成计算瓶颈(港大港中文字节)
论文链接:https://arxiv.org/pdf/2502.05179 项目链接:https://github.com/FoundationVision/FlashVideo 亮点直击 提出了 FlashVideo,一种将视频生成解耦为两个目标的方法:提示匹配度和视觉质量。通过在两个阶段分别调整模型规模…...

Qt的QTabWidget的使用
在PyQt5中,QTabWidget 是一个用于管理多个选项卡页面的容器控件。以下是其使用方法的详细说明和示例: 1. 基本用法 import sys from PyQt5.QtWidgets import QApplication, QMainWindow, QTabWidget, QWidget, QLabel, QVBoxLayoutclass MainWindow(QMa…...

Next.js【详解】获取数据(访问接口)
Next.js 中分为 服务端组件 和 客户端组件,内置的获取数据各不相同 服务端组件 方式1 – 使用 fetch export default async function Page() {const data await fetch(https://api.vercel.app/blog)const posts await data.json()return (<ul>{posts.map((…...

反向代理模块kd
1 概念 1.1 反向代理概念 反向代理是指以代理服务器来接收客户端的请求,然后将请求转发给内部网络上的服务器,将从服务器上得到的结果返回给客户端,此时代理服务器对外表现为一个反向代理服务器。 对于客户端来说,反向代理就相当于…...

leaflet前端初始化项目
1、通过npm安装leaflet包,或者直接在项目中引入leaflet.js库文件。 npm 安装:npm i leaflet 如果在index.html中引入leaflet.js,在项目中可以直接使用变量L. 注意:尽量要么使用npm包,要么使用leaflet.js库,两者一起使用容易发生…...
)
CMS DTcms 靶场(弱口令、文件上传、tasklist提权、开启远程桌面3389、gotohttp远程登录控制)
环境说明 攻击机kali:192.168.111.128 信息收集 主机发现 ┌──(root㉿kali-plus)-[~/Desktop] └─# nmap -sP 192.168.111.0/24 Starting Nmap 7.94SVN ( https://nmap.org ) at 2024-11-23 14:57 CST Nmap scan report for 192.168.111.1 Host is up (0.00039s latenc…...

Docker 入门与实战:从安装到容器管理的完整指南
🚀 Docker 入门与实战:从安装到容器管理的完整指南 🌟 📖 简介 在现代软件开发中,容器化技术已经成为不可或缺的一部分。而 Docker 作为容器化领域的领头羊,以其轻量级、高效和跨平台的特性,深…...

git删除本地分支
一、命令方式 1、查看本地分支 git branch 2、切换到一个不删除的分支 git checkout branch_name 3、强制删除分支 git branch -D local_branch_name 二、工具方式 1、选择"Browse references",右键"Delete branch"...

spring cloud gateway限流常见算法
目录 一、网关限流 1、限流的作用 1. 保护后端服务 2. 保证服务质量 (QoS) 3. 避免滥用和恶意攻击 4. 减少资源浪费 5. 提高系统可扩展性和稳定性 6. 控制不同用户的访问频率 7. 提升用户体验 8. 避免API滥用和负载过高 9. 监控与分析 10. 避免系统崩溃 2、网关限…...

本地使用docker部署DeepSeek大模型
1、相关技术介绍 1.1、RAG RAG(Retrieval Augmented Generation),即“检索,增强,生成”,用于提升自然语言处理任务的性能。其核心思想是通过检索相关信息来增强生成模型的能力,具体步骤如下&am…...

C++ 设计模式-外观模式
外观模式的定义 外观模式是一种 结构型设计模式,它通过提供一个简化的接口来隐藏系统的复杂性。外观模式的核心思想是: 封装复杂子系统:将多个复杂的子系统或组件封装在一个统一的接口后面。提供简单接口:为客户端提供一个更简单、更易用的接口,而不需要客户端直接与复杂…...

【Linux网络编程】应用层协议HTTP(请求方法,状态码,重定向,cookie,session)
🎁个人主页:我们的五年 🔍系列专栏:Linux网络编程 🌷追光的人,终会万丈光芒 🎉欢迎大家点赞👍评论📝收藏⭐文章 Linux网络编程笔记: https://blog.cs…...

SQL进阶技巧:如何统计用户跨端消费行为?
目录 0 问题描述 2 问题剖析 技术难点解析 3 完整解决方案 步骤1:构造全量日期平台组合 步骤2:用户行为标记 步骤3:最终关联聚合 4 核心技巧总结 5 复杂度评估 往期精彩 0 问题描述 支出表: Spending +-------------+---------+ | Column Name | Type | +-----…...

Fiddler笔记
文章目录 一、与F12对比二、核心作用三、原理四、配置1.Rules:2.配置证书抓取https包3.设置过滤器4、抓取App包 五、模拟弱网测试六、调试1.线上调试2.断点调试 七、理论1.四要素2.如何定位前后端bug 注 一、与F12对比 相同点: 都可以对http和https请求进行抓包分析…...

基于SpringBoot+Vue的老年人体检管理系统的设计与实现(源码+SQL脚本+LW+部署讲解等)
专注于大学生项目实战开发,讲解,毕业答疑辅导,欢迎高校老师/同行前辈交流合作✌。 技术范围:SpringBoot、Vue、SSM、HLMT、小程序、Jsp、PHP、Nodejs、Python、爬虫、数据可视化、安卓app、大数据、物联网、机器学习等设计与开发。 主要内容:…...

51c自动驾驶~合集51
我自己的原文哦~ https://blog.51cto.com/whaosoft/13320191 #毫末最新OAD 轨迹偏移学习助力端到端新SOTA~ 端到端自动驾驶技术在近年来取得了显著进展。在本研究中,我们提出了轨迹偏移学习,将传统的直接预测自车轨迹,转换为预测相对于…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...

区块链技术概述
区块链技术是一种去中心化、分布式账本技术,通过密码学、共识机制和智能合约等核心组件,实现数据不可篡改、透明可追溯的系统。 一、核心技术 1. 去中心化 特点:数据存储在网络中的多个节点(计算机),而非…...

二维FDTD算法仿真
二维FDTD算法仿真,并带完全匹配层,输入波形为高斯波、平面波 FDTD_二维/FDTD.zip , 6075 FDTD_二维/FDTD_31.m , 1029 FDTD_二维/FDTD_32.m , 2806 FDTD_二维/FDTD_33.m , 3782 FDTD_二维/FDTD_34.m , 4182 FDTD_二维/FDTD_35.m , 4793...

02.运算符
目录 什么是运算符 算术运算符 1.基本四则运算符 2.增量运算符 3.自增/自减运算符 关系运算符 逻辑运算符 &&:逻辑与 ||:逻辑或 !:逻辑非 短路求值 位运算符 按位与&: 按位或 | 按位取反~ …...

WebRTC调研
WebRTC是什么,为什么,如何使用 WebRTC有什么优势 WebRTC Architecture Amazon KVS WebRTC 其它厂商WebRTC 海康门禁WebRTC 海康门禁其他界面整理 威视通WebRTC 局域网 Google浏览器 Microsoft Edge 公网 RTSP RTMP NVR ONVIF SIP SRT WebRTC协…...
