LeetCodehot 力扣热题100
class Solution {
public:int max_sum = INT_MIN; // 初始化为最小值,确保能够处理所有可能的路径和int maxPathSum(TreeNode* root) {dfs(root);return max_sum;}int dfs(TreeNode* root) {if (root == nullptr) return 0; // 如果是空节点,返回0// 递归计算左子树和右子树的最大路径和,负值则不贡献路径和int left = max(0, dfs(root->left)); // 只考虑正路径int right = max(0, dfs(root->right)); // 只考虑正路径// 计算当前节点的最大路径和,包括根节点与左、右子树的路径max_sum = max(max_sum, root->val + left + right);// 返回当前节点的最大贡献值return root->val + max(left, right); // 返回当前节点的最大路径和(要么包括左子树,要么右子树)}
};路径上的节点最多有两个相邻节点。
好的,接下来我会详细解析你之前提到的 二叉树最大路径和 代码的思路。
问题说明
最大路径和问题的目标是:在一个二叉树中找到一条路径,使得路径上的节点值的和最大。这条路径可以通过任意节点,不需要从根节点开始,并且路径可以穿越树的多个分支。
• max_sum 作为一个全局变量,用来存储二叉树中计算出来的最大路径和。初始化为 0,代表我们初始时尚未计算任何路径的和。
2. maxPathSum 函数
int maxPathSum(TreeNode* root) {
dfs(root); // 从根节点开始,递归计算最大路径和
return max_sum; // 返回最大路径和
}
• maxPathSum 是主要的接口函数,它接收二叉树的根节点 root 作为输入,调用 dfs 函数计算路径和。
• 调用 dfs(root) 会触发对整个树的深度优先搜索。
• 最后返回 max_sum,这个变量会保存二叉树中遍历得到的最大路径和。
3. 深度优先搜索 dfs 函数
int dfs(TreeNode* root) {
if (root == nullptr) return 0; // 递归边界:如果节点为空,路径和为0
• dfs 是一个递归函数,负责从当前节点计算出其左右子树的路径和,并更新 max_sum。
• 如果当前节点是 nullptr(即为空节点),直接返回 0,因为空节点对路径和没有任何贡献。
int left = max(0, dfs(root->left)); // 计算左子树的最大路径和,若为负数则不贡献,返回0
int right = max(0, dfs(root->right)); // 计算右子树的最大路径和,若为负数则不贡献,返回0
• 计算当前节点的左子树和右子树的最大路径和。
• 对于每个子树,我们希望只考虑正路径和(即如果某个子树的路径和是负数,那么我们就不考虑这条路径)。因此,使用 max(0, dfs(...)) 来确保如果子树的路径和为负数,则返回 0,表示我们不选取该子树。
• dfs(root->left) 和 dfs(root->right) 分别递归地计算左子树和右子树的最大路径和。
max_sum = max(max_sum, root->val + left + right); // 以当前节点为根的路径和
• 现在我们计算的是通过当前节点 root 的路径和,这个路径包括:
• 当前节点的值 root->val
• 左子树的最大路径和 left
• 右子树的最大路径和 right
• max_sum 会更新为当前路径和和之前的最大路径和中的较大值。
return root->val + max(left, right); // 返回当前节点的最大路径和
• 由于路径不能跨越多个分支,因此我们只能选择单边(左子树或右子树)继续延伸路径。返回当前节点的最大路径和时,我们只选择左子树和右子树中的较大者:
• root->val + max(left, right) 表示包括当前节点和其较大子树路径和的最大路径和。
4. 递归的执行流程
• 从根节点开始递归。
• 对于每个节点:
• 计算左右子树的最大路径和(递归调用 dfs)。
• 更新全局变量 max_sum。
• 返回当前节点的最大路径贡献(选择左子树或右子树的较大路径)。
• 最终 max_sum 就包含了整棵树的最大路径和。
代码执行流程(示例)
假设有以下二叉树:
1
/ \
2 3
/ \
4 5
1. 调用 maxPathSum(root),根节点是 1:
• 进入 dfs(1)。
2. dfs(1):
• 左子树是 2,右子树是 3,开始计算左右子树的路径和。
3. 计算 dfs(2)(左子树):
• 左子树是 4,右子树是 5,继续递归。
4. 计算 dfs(4):
• 节点 4 没有子树,返回 4。
5. 计算 dfs(5):
• 节点 5 没有子树,返回 5。
6. 计算 dfs(2):
• left = 4,right = 5,节点 2 的路径和是 2 + 4 + 5 = 11。
• 更新 max_sum = 11。
• 返回 2 + max(4, 5) = 7。
7. 计算 dfs(3)(右子树):
• 节点 3 没有子树,返回 3。
8. 计算 dfs(1)(根节点):
• left = 7,right = 3,节点 1 的路径和是 1 + 7 + 3 = 11,max_sum 不变。
• 返回 1 + max(7, 3) = 8。
9. 最终结果:
• max_sum = 11,即树中的最大路径和是 4 -> 2 -> 5 或 4 -> 2 -> 1 -> 3。
总结
1. 深度优先搜索:通过递归遍历树中的每个节点,计算以每个节点为根的最大路径和。
2. 路径和的更新:对于每个节点,计算包括其左右子树的路径和,并更新全局最大路径和 max_sum。
3. 递归的返回值:每个节点返回的路径和代表它向上回溯的贡献,它是当前节点值与左、右子树最大路径和中的较大者之和。
这种方法的时间复杂度是 O(n),其中 n 是二叉树的节点数,因为每个节点只会被访问一次。
相关文章:

LeetCodehot 力扣热题100
class Solution { public:int max_sum INT_MIN; // 初始化为最小值,确保能够处理所有可能的路径和int maxPathSum(TreeNode* root) {dfs(root);return max_sum;}int dfs(TreeNode* root) {if (root nullptr) return 0; // 如果是空节点,返回0// 递归…...

解锁 AIoT 无限可能,乐鑫邀您共赴 Embedded World 2025
2025 年 3 月 11-13 日,全球规模最大的嵌入式展览会——Embedded World 2025 将在德国纽伦堡盛大开幕。作为物联网和嵌入式技术领域的领先企业,乐鑫信息科技 (688018.SH) 将展示在 AI LLM、HMI、双频 Wi-Fi 6、低功耗 MCU 和 Matter 等领域的最新技术及解…...

C# 背景 透明 抗锯齿 (效果完美)
主要是通过 P/Invoke 技术调用 Windows API 函数 gdi32.dll/user32.dll,同时定义了一些结构体来配合这些 API 函数的使用,常用于处理图形绘制、窗口显示等操作。 运行查看效果 局部放大,抗锯齿效果很不错,尾巴毛毛清晰可见。 using System; u…...

Debezium:实时数据捕获与同步的利器
一、什么是 Debezium Debezium 是一个开源的分布式平台,专门用于捕获数据库中的数据变更。它通过读取数据库的事务日志,能够以非侵入性的方式捕获数据库中发生的所有变化,并将这些变化转化为事件流,实时推送到像 Kafka 这样的消息…...

Word中接入大模型教程
前言 为什么要在word中接入大模型呢? 个人觉得最大的意义就是不用来回切换与复制粘贴了吧。 今天分享一下昨天实践的在word中接入大模型的教程。 在word中接入大模型最简单的方式就是使用vba。 vba代码要做的事,拆分一下就是: 获取用户…...

Centos修改ip
1 查看ip [rootlocalhost ~]# ip addr2 root账号修改ip [rootlocalhost ~]# su [rootlocalhost ~]# cd /etc/sysconfig/network-scripts/ [rootlocalhost network-scripts]# llvi编辑ifcfg-ens33 3 重启网卡 [rootlocalhost network-scripts]# systemctl restart network...

uni-app小程序开发 基础知识2
目标: 构建一个文章发表平台。 我们先来写一个静态框架。 以下是 首页初代码文章列表页代码: <template><view class"content"><!-- 轮播图 --><swiper class"swiper-container" autoplay"true"…...

第4章 4.1 Entity Framework Core概述
4.1.1 什么是ORM ORM (object tralstional mapping ,对象关系映射)中的“对象”指的就是C#中的对象,而“关系”是关系型数据库,“映射”指搭建数据库与C#对象之间的“桥梁”。 比如使用ORM ,可以通过创建C#对象的方式把数据插入数据库而不需…...

在 Spring Boot 中使用 `@Autowired` 和 `@Bean` 注解
文章目录 在 Spring Boot 中使用 Autowired 和 Bean 注解示例背景 1. 定义 Student 类2. 配置类:初始化 Bean3. 测试类:使用 Autowired 注解自动注入 Bean4. Spring Boot 的自动装配5. 总结 在 Spring Boot 中使用 Autowired 和 Bean 注解 在 Spring Bo…...

Langchain vs. LlamaIndex:哪个在集成MongoDB并分析资产负债表时效果更好?
Langchain vs. LlamaIndex:哪个在集成MongoDB并分析资产负债表时效果更好? 随着大语言模型(LLM)在实际应用中的普及,许多开发者开始寻求能够帮助他们更高效地开发基于语言模型的应用框架。在众多框架中,La…...

Java 中的内存泄漏问题及解决方案
在 Java 中,内存泄漏(Memory Leak)是指在程序运行过程中,某些对象已经不再使用,但由于引用仍然存在,这些对象无法被垃圾回收器回收,从而导致内存无法释放,最终可能导致系统性能下降甚…...
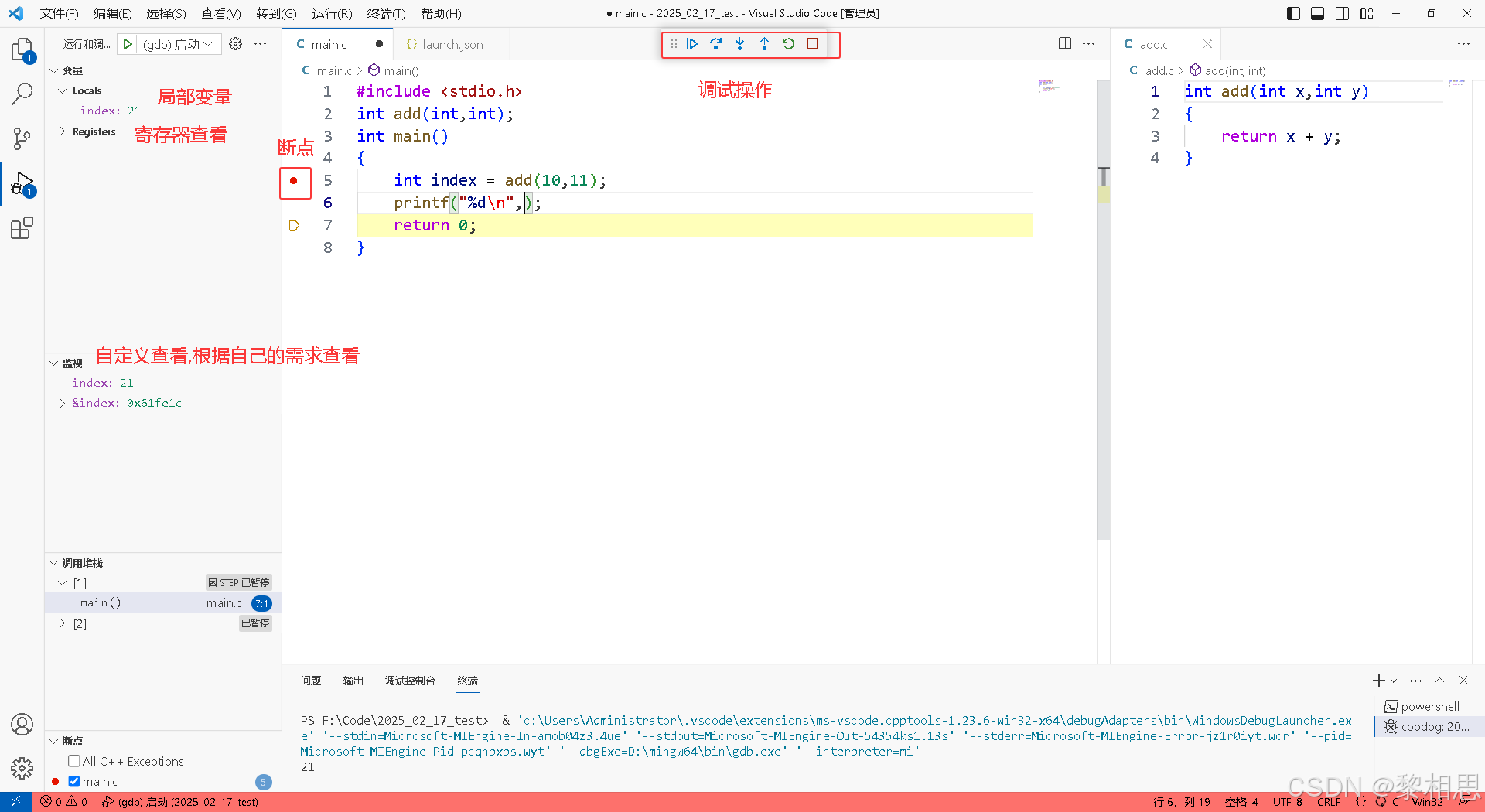
VS Code 如何搭建C/C++开发环境
目录 1.VS Code是什么 2. VS Code的下载和安装 2.1 下载和安装 2.2.1 下载 2.2.2 安装 2.2 环境的介绍 2.3 安装中文插件 3. VS Code配置C/C开发环境 3.1 下载和配置MinGW-w64编译器套件 3.1.1 下载 3.1.2 配置 3.2 安装C/C插件 3.3 重启VSCode 4. 在VSCode上编写…...

【Linux C/C++开发】Linux系统轻量级的队列缓存mqueue
前言 开发设计时,通常会对业务流程进行模块化,有些流程之间,不要求同步,但又需要传递信息时,如果存储到数据库,效率降低很多,如果是存放在内存是最好的。此时可以选择系统的IPC(进程…...

排查生产sql查询缓慢
生产投产检验,发现查询客户明细的接口数据响应需要5秒以上,通过接口可以查询到详细的后端代码 1. 先排查后端的代码实现,并未出现复杂逻辑,那么就应该是sql的问题 2. 通过explain对sql进行解析,发现sql没有走索引 3.…...

idea从远程gitee拉取项目
文章目录 从gitee上面拿到项目地址填写远程地址,并且设置项目保存位置拉取成功 从gitee上面拿到项目地址 填写远程地址,并且设置项目保存位置 拉取成功...

【UCB CS 61B SP24】Lecture 5 - Lists 3: DLLists and Arrays学习笔记
本文内容为构建双向循环链表、使用 Java 的泛型将其优化为通用类型的链表以及数组的基本语法介绍。 1. 双向链表 回顾上一节课写的代码,当执行 addLast() 与 getLast() 方法时需要遍历链表,效率不高,因此可以添加一个指向链表末尾的索引&am…...

软件测试与软件开发之间的关系
软件测试与软件开发的关系 软件测试(Software Testing)与软件开发(Software Development)是软件工程中的两个核心环节,它们相辅相成,确保软件的质量和功能满足需求。以下是两者之间的关系解析:…...

QT 建立一片区域某种颜色
绘制一个位于(50, 50)的200x200的红色矩形 #include "widget.h" #include "ui_widget.h" #include <QPainter>Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this);update(); }Widget::~Widget() {delete…...

LeetCode--23. 合并 K 个升序链表【堆和分治】
23. 合并 K 个升序链表 给你一个链表数组,每个链表都已经按升序排列。 请你将所有链表合并到一个升序链表中,返回合并后的链表。 正文 这道题有多种解决方案 堆 比较容易,又比较直观的就是堆排序,将每个节点加入最小根堆中&…...

tp6上传文件大小超过了最大值+验证文件上传大小和格式函数
问题: 最近用tp6的文件上传方法上传文件时报文件过大错误。如下所示: $file $this->request->file(file);{"code": 1,"msg": "上传文件大小超过了最大值!","data": {"code": 1,&q…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...
