【机器学习】13.十大算法之一K均值算法(K-means)聚类详细讲解
【机器学习】13.十大算法之一K均值算法(K-means)聚类详细讲解
- 一·摘要
- 二·个人简介
- 三·K-均值聚类(K-means)
- 3.1-K均值算法的基本原理
- 3.1.1- 聚类分析的目标
- 3.1.2- K - means算法算法原理
- 四·K-means聚类算法的收敛性
- 五·证明K均值算法的收敛性
- 六·K-means聚类算法怎么选择合适的K值
- 6.1- 肘部法则(Elbow Method)
- 6.2- 轮廓系数(Silhouette Coefficient)
- 6.3- 平均轮廓法
- 七·总结
一·摘要

K-means聚类算法是一种经典的无监督学习算法,它通过迭代过程来对数据进行聚类。聚类的目的在于把具有相似特征的数据分为若干组或簇,使得同一组内数据的相似度尽可能高,而不同组之间的数据相似度尽可能低。
该算法的基本思想是:随机选择K个数据点作为初始聚类中心,接着将每个数据点分配到最近的簇中心,然后重新计算每个簇的中心点,此过程不断迭代进行,直至满足停止条件,即簇中心的位置不再发生显著变化或达到预设的迭代次数 。
K-means算法的实现主要包括两个关键步骤:数据点的分配和簇中心的更新。在数据点的分配阶段,算法将计算每个数据点与各个簇中心的距离,并将数据点划分到距离最近的簇中。在簇中心的更新阶段,算法会根据新分配的数据点重新计算各簇的中心点,通常是取簇中所有点的均值作为新的簇中心。
二·个人简介
🏘️🏘️个人主页:以山河作礼。
🎖️🎖️:Python领域新星创作者,CSDN实力新星认证,CSDN内容合伙人,阿里云社区专家博主,新星计划导师,在职数据分析师。
💕💕悲索之人烈焰加身,堕落者不可饶恕。永恒燃烧的羽翼,带我脱离凡间的沉沦。


| 类型 | 专栏 |
|---|---|
| Python基础 | Python基础入门—详解版 |
| Python进阶 | Python基础入门—模块版 |
| Python高级 | Python网络爬虫从入门到精通🔥🔥🔥 |
| Web全栈开发 | Django基础入门 |
| Web全栈开发 | HTML与CSS基础入门 |
| Web全栈开发 | JavaScript基础入门 |
| Python数据分析 | Python数据分析项目🔥🔥 |
| 机器学习 | 机器学习算法🔥🔥 |
| 人工智能 | 人工智能 |
三·K-均值聚类(K-means)
3.1-K均值算法的基本原理
3.1.1- 聚类分析的目标
聚类分析旨在将数据集划分为若干个组或簇,使得同一簇内的数据对象具有较高的相似性,而不同簇之间的数据对象则存在较大的差异性。通过聚类分析,能够揭示数据的潜在模式、发现数据内在的结构规律,从而为后续的数据分析和决策提供有力支持。

K - means 算法的目标是将数据集划分为 K 个不相交的聚类簇(clusters)。它通过迭代的方式,使得同一聚类簇内的数据点之间的相似度(通常是距离的倒数)尽可能高,而不同聚类簇之间的相似度尽可能低。这样可以帮助我们发现数据中的内在结构和模式,例如在客户细分中,可以根据客户的特征将他们划分为不同的群体,以便采取针对性的营销策略。
3.1.2- K - means算法算法原理
- 初始化
随机选择 K 个数据点作为初始聚类中心(cluster centers)。这些初始中心的选择可能会对最终的聚类结果产生一定的影响。在对二维空间中的点进行聚类时,如果初始中心恰好位于数据分布较为密集的区域,可能会更快地收敛到较好的聚类结果。
- 分配数据点到最近的聚类中心
对于数据集中的每一个数据点,计算它与各个聚类中心的距离(通常采用欧氏距离,但也可以使用其他距离度量如曼哈顿距离等)。然后将该数据点分配给距离它最近的聚类中心所在的聚类簇。如果有三个聚类中心 C1、C2 和 C3,对于一个数据点 P,如果它到 C2 的距离最小,那么 P 就被分配到以 C2 为中心的聚类簇。
- 更新聚类中心
当所有的数据点都被分配到相应的聚类簇后,重新计算每个聚类簇的中心。新的聚类中心是该聚类簇内所有数据点的均值。以一维数据为例,假设一个聚类簇包含数据点 {2,4,6},那么新的聚类中心就是(2 + 4 + 6)/3 = 4。
- 迭代
重复步骤 2 和步骤 3,直到满足一定的停止条件。常见的停止条件包括:聚类中心的变化小于某个阈值、达到预设的最大迭代次数或者聚类结果不再发生变化。当连续两次迭代后,所有聚类中心的位置变化都不超过 0.001 时,就可以认为算法已经收敛,停止迭代。

四·K-means聚类算法的收敛性
K-means聚类算法的收敛性是指算法在有限次迭代后达到一个稳定的状态,即聚类中心不再发生显著变化,或者目标函数(通常是总误差平方和)不再显著减小。
以下是关于K-means聚类算法收敛性的详细解释:
- 目标函数
K-means算法的目标函数是所有数据点到其所属聚类中心的距离平方之和,定义为:

- 收敛条件
K-means算法在以下情况下停止迭代:
- 目标函数稳定:当连续两次迭代的目标函数值变化小于某个预设的阈值时,认为算法收敛。
- 最大迭代次数:当达到预设的最大迭代次数时,算法停止。
五·证明K均值算法的收敛性
K-means算法的收敛性可以通过以下两点来证明:
- 目标函数单调递减:在每次迭代中,分配步骤确保每个数据点到其所属聚类中心的距离不会增加,因此目标函数值不会增加。更新步骤通过计算均值来最小化每个聚类簇内的距离平方和,从而进一步减小目标函数值。因此,目标函数值在每次迭代中都是单调递减的。
- 目标函数有下界:目标函数值是非负的,因为它是距离平方的和。因此,目标函数值有下界(即0)。
由于目标函数值在每次迭代中单调递减且有下界,根据单调有界数列的收敛定理,K-means算法的目标函数值必然收敛到某个值。
六·K-means聚类算法怎么选择合适的K值
6.1- 肘部法则(Elbow Method)
肘部法通过观察不同K值下的总误差平方和(SSE)变化来选择K值。随着K值的增加,SSE会逐渐减小,但当K值增加到一定程度后,SSE的下降速度会显著减缓,形成一个“肘部”点。这个点对应的K值通常被认为是最优的。
步骤:
- 选择一个K值范围(如1到10)。
- 对每个K值运行K-means算法,计算SSE。
- 绘制K值与SSE的曲线图。
- 找到曲线的“肘部”点,即SSE下降速度开始减缓的点。
代码示例:
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs# 创建数据集
X, _ = make_blobs(n_samples=300, centers=4, cluster_std=0.60, random_state=42)# 初始化SSE列表
sum_of_squared_errors = []
cluster_range = range(2, 12) # 调整K值范围# 计算不同K值的SSE
for num_clusters in cluster_range:kmeans_model = KMeans(n_clusters=num_clusters, random_state=42)kmeans_model.fit(X)sum_of_squared_errors.append(kmeans_model.inertia_)# 绘制肘部图
plt.figure(figsize=(8, 5))
plt.plot(cluster_range, sum_of_squared_errors, marker='o', linestyle='-', color='blue')
plt.title('Elbow Method to Determine Optimal K')
plt.xlabel('Number of Clusters (K)')
plt.ylabel('Sum of Squared Errors (SSE)')
plt.grid(True)
plt.show()

6.2- 轮廓系数(Silhouette Coefficient)
轮廓系数用于衡量数据点在所属聚类簇内的紧密程度以及与其他聚类簇的分离程度。轮廓系数的值介于-1到1之间,值越接近1,表示聚类效果越好。
操作步骤:
- 对一系列K值(例如2到10)运行K-means算法。
- 计算每个K值的轮廓系数。
- 选择轮廓系数最高的K值作为最佳聚类数。
示例代码:
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs
from sklearn.metrics import silhouette_score# 创建模拟数据集
data, _ = make_blobs(n_samples=300, centers=4, cluster_std=0.60, random_state=42)# 初始化存储轮廓系数的列表
silhouette_results = []# 遍历不同的聚类数K
for num_clusters in range(2, 11): # 聚类数从2到10kmeans = KMeans(n_clusters=num_clusters, random_state=42)labels = kmeans.fit_predict(data)silhouette_avg = silhouette_score(data, labels) # 计算轮廓系数silhouette_results.append(silhouette_avg)# 绘制轮廓系数与聚类数K的关系图
plt.figure(figsize=(8, 5))
plt.plot(range(2, 11), silhouette_results, marker='s', linestyle='-', color='purple', linewidth=1.5)
plt.title('Optimal K Selection using Silhouette Score', fontsize=14)
plt.xlabel('Number of Clusters (K)', fontsize=12)
plt.ylabel('Silhouette Score', fontsize=12)
plt.xticks(range(2, 11))
plt.grid(axis='y', linestyle='--', alpha=0.7)
plt.show()

6.3- 平均轮廓法
平均轮廓系数法是一种评估聚类质量的方法,它综合考虑了每个数据点在所属聚类簇内的紧密程度以及与其他聚类簇的分离程度。轮廓系数的值范围为[-1, 1],值越接近1,表示聚类效果越好
轮廓系数的计算步骤:
- 计算a(i):对于每个数据点 i,计算其到同一聚类簇内其他点的平均距离 a(i)。
- 计算b(i):计算数据点 i 到最近的其他聚类簇的所有点的平均距离 b(i)。
计算轮廓系数s(i):对于每个数据点 i,其轮廓系数 s(i) 定义为:

其中,s(i) 接近1表示数据点 i 被很好地聚类;接近0表示数据点 i 在两个聚类簇之间;为负值则表示数据点 i 可能被错误地分配到当前聚类簇。
计算平均轮廓系数:整个数据集的平均轮廓系数是所有数据点轮廓系数的均值,用于评估整体聚类效果
代码示例:
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs
from sklearn.metrics import silhouette_score# 生成模拟数据集
data_points, _ = make_blobs(n_samples=500, centers=5, cluster_std=0.8, random_state=123)# 初始化用于存储轮廓系数的列表
avg_silhouette_scores = []# 测试不同聚类数K的范围
k_values = range(2, 12) # 从2到11
for k in k_values:# 对每个K值运行K-means聚类kmeans_model = KMeans(n_clusters=k, random_state=123)cluster_labels = kmeans_model.fit_predict(data_points)# 计算平均轮廓系数avg_score = silhouette_score(data_points, cluster_labels)avg_silhouette_scores.append(avg_score)# 绘制平均轮廓系数与K值的关系图
plt.figure(figsize=(10, 6))
plt.plot(k_values, avg_silhouette_scores, marker='s', linestyle='-', color='orange', linewidth=2)
plt.title('Average Silhouette Score vs. Number of Clusters (K)', fontsize=14)
plt.xlabel('Number of Clusters (K)', fontsize=12)
plt.ylabel('Average Silhouette Score', fontsize=12)
plt.xticks(k_values)
plt.grid(axis='both', linestyle='--', alpha=0.7)
plt.show()

七·总结
K-means聚类算法是一种简单而强大的无监督学习方法,广泛应用于各种数据挖掘任务中。通过理解其基本原理和收敛性,我们可以更好地应用该算法。选择合适的K值是提高聚类效果的关键。肘部法则、轮廓系数和平均轮廓法等方法为我们提供了有效的工具来确定最佳的K值。在实际应用中,建议结合多种方法和领域知识,以获得最佳的聚类结果。
相关文章:

【机器学习】13.十大算法之一K均值算法(K-means)聚类详细讲解
【机器学习】13.十大算法之一K均值算法(K-means)聚类详细讲解 一摘要二个人简介三K-均值聚类(K-means)3.1-K均值算法的基本原理3.1.1- 聚类分析的目标3.1.2- K - means算法算法原理 四K-means聚类算法的收敛性五证明K均值算法的收…...

Spring扩展点之Mybatis整合模拟
Spring扩展点之Mybatis整合 单独使用MyBaitis模拟整合MyBatis到Spring 单独使用MyBaitis 通过配置文件生成sqlSessionFactory,用sqlSessionFactory开启session。通过session获取到mapper执行对应的sql。 InputStream inputStream Resources.getResourceAsStream(…...

.NET MVC实现电影票管理
.NET MVC(Model-View-Controller)是微软推出的基于 Model-View-Controller 设计模式的 Web 应用框架,属于 ASP.NET Core 的重要组成部分。其核心目标是通过清晰的分层架构实现 高内聚、低耦合 的开发模式,适用于构建可扩展的企业级…...

自媒体账号管理工具:创作罐头使用指南
创作罐头使用指南 1. 关于创作罐头 创作罐头是免费的一站式自媒体运营工具,支持各大自媒体平台多账号管理、全网爆文库、原创检测、视频一键分发、团队管理、各平台数据分析等功能。 2. 安装与注册 2.1. 如何安装创作罐头 从我们的官网下载并安装软件 www.czgts.…...

基于数据可视化+SpringBoot+安卓端的数字化OA公司管理平台设计和实现
博主介绍:硕士研究生,专注于信息化技术领域开发与管理,会使用java、标准c/c等开发语言,以及毕业项目实战✌ 从事基于java BS架构、CS架构、c/c 编程工作近16年,拥有近12年的管理工作经验,拥有较丰富的技术架…...
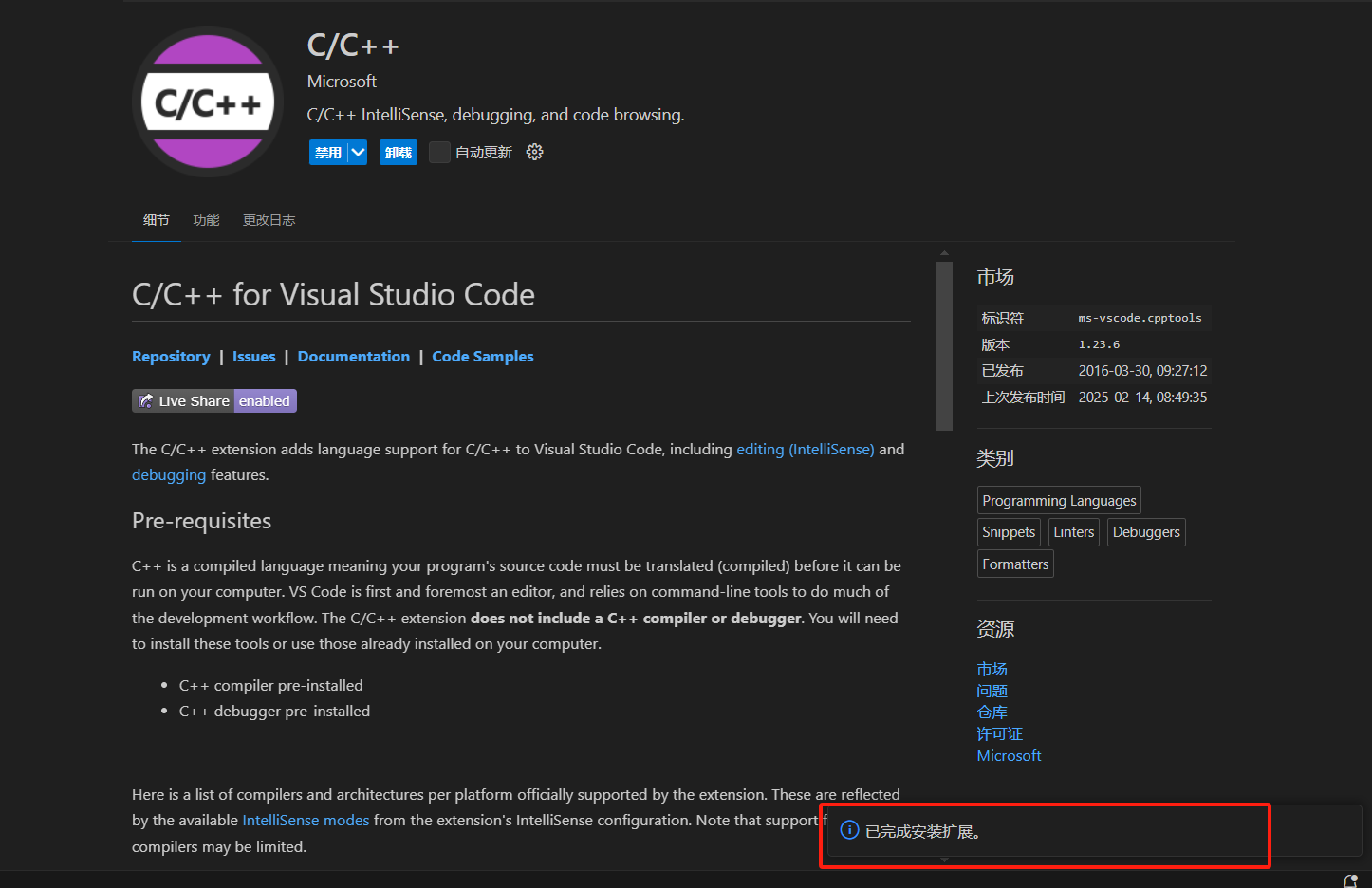
VSCode离线安装插件
最近在其他电脑设备上部署vscode环境出现问题,在vscode里直接安装插件失败,软件提示如下:(此前已经用此方法安装过中文插件) 这里我们选择手动下载,会自动在浏览器中跳转到该插件的下载链接并自动下载插件&…...

基于Hadoop的汽车大数据分析系统设计与实现【爬虫、数据预处理、MapReduce、echarts、Flask】
文章目录 有需要本项目的代码或文档以及全部资源,或者部署调试可以私信博主 项目介绍爬虫数据概览HIve表设计Cars Database Tables 1. cars_data2. annual_sales_volume3. brand_sales_volume4. city_sales_volume5. sales_volume_by_year_and_brand6. sales_distri…...

SHELL32!Shell_MergeMenus函数分析
SHELL32!Shell_MergeMenus函数分析 UINT Shell_MergeMenus( [in] HMENU hmDst, [in] HMENU hmSrc, UINT uInsert, UINT uIDAdjust, UINT uIDAdjustMax, ULONG uFlags ); 参数 [in] hmDst 类型: HMENU 要向其添加 hmSrc…...

华为云deepseek大模型平台:deepseek满血版
华为云硅基流动使用Chatbox接入DeepSeek-R1满血版671B 1、注册: 华为云deepseek大模型平台注册:https://cloud.siliconflow.cn/i/aDmz6aVN 说明:填写邀请码的话邀请和被邀请的账号都会获得2000 万 Tokens;2个帐号间不会与其他关联…...

AutoGen 技术博客系列 八:深入剖析 Swarm—— 智能体协作的新范式
本系列博文在掘金同步发布, 更多优质文章,请关注本人掘金账号: 人肉推土机的掘金账号 AutoGen系列一:基础介绍与入门教程 AutoGen系列二:深入自定义智能体 AutoGen系列三:内置智能体的应用与实战 AutoGen系列四&am…...

从零开始开发纯血鸿蒙应用之网页浏览
从零开始开发纯血鸿蒙应用 〇、前言一、优化菜单交互1、BuilderFunction.ets2、改造 PageTitleBar 二、网址打开1、方式选择1、使用浏览器打开2、内部打开2.1、声明权限2.2、封装 WebViewPage2.2.1、组件字段2.2.2、aboutToAppear2.2.3、onBackPress2.2.4、标题栏2.2.4、网页内…...

【大模型LLM】DeepSeek LLM Scaling Open-Source Language Models with Longtermism
深度探索LLM:以长期主义扩展开源语言模型 0.论文摘要 开源大语言模型(LLMs)的快速发展确实令人瞩目。然而,以往文献中描述的扩展规律得出了不同的结论,这为LLMs的扩展蒙上了一层阴影。我们深入研究了扩展规律&#…...

分布式事务-本地消息表学习与落地方案
本文参考: 数据库事务系列04-本地消息表实现分布式事务 基础概念 本地消息表实现分布式事务最终一致性的核心:是通过上游本地事务的原子性持久性,配合中间件的重试机制,从而实现调用下游的最终一致性。 这里有几个要点可以解析一…...

Debezium系列之:记录一次源头数据库刷数据,造成数据丢失的原因
Debezium系列之:记录一次源头数据库刷数据,造成数据丢失的原因 一、背景二、查看topic日志信息三、结论四、解决方法一、背景 源头数据库在很短的时间内刷了大量的数据,部分数据在hdfs丢失了 理论上debezium数据采集不会丢失,就需要排查数据链路某个节点是否有数据丢失。 …...

PHP约课健身管理系统小程序源码
🏋️♂️ 约课健身管理系统小程序:重塑健身预约体验,引领数字化健身新时代 一款基于ThinkPHPUniapp框架,由米扬精心雕琢的约课健身管理系统小程序,专为健身房、健身工作室、运动会所、运动场馆、瑜伽馆、拳馆等泛健…...

Java之泛型
文章目录 首先接着上一篇(集合)文章,来个非常牛逼的易错题传统集合问题分析泛型快速入门案例泛型介绍泛型的好处泛型的语法泛型的声明泛型的实例化泛型使用举例泛型使用的注意事项和细节 自定义泛型自定义泛型方法 自定义泛型接口自定义泛型方…...

图论 之 最小生成树
文章目录 题目1584.连接所有点的最小费用 最小生成树MST,有两种算法进行求解,分别是Kruskal算法和Prim算法Kruskal算法从边出发,适合用于稀疏图Prim算法从顶点出发,适合用于稠密图:基本思想是从一个起始顶点开始&#…...

STM32-有关内存堆栈、map文件
STM32堆栈空间大小设置_stm32堆栈分配大小-CSDN博客 STM32堆栈的大小及内存四(五)区的分析 - 天街小雨润地狠 - 博客园 .map文件的位置...

Linux系统中常见的词GNU是什么意思?
GNU 是 “GNU’s Not Unix” 的递归缩写,它是一个自由软件项目,旨在创建一个完全自由的操作系统。这个名字反映了GNU项目的核心理念:它试图创建一个类Unix的系统,但不是Unix本身。 GNU 项目由 理查德斯托曼(Richard S…...

【个人开源】——从零开始在高通手机上部署sd(二)
代码:https://github.com/chenjun2hao/qualcomm.ai 推理耗时统计 单位/ms 硬件qnncpu_clipqnncpu_unetqnncpu_vaehtp_cliphtp_unethtp_vae骁龙8 gen124716.994133440.39723.215411.097696.327 1. 下载依赖 下载opencv_x64.tar,提取码: rrbp下载opencv_aarch64.t…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...

Linux系统部署KES
1、安装准备 1.版本说明V008R006C009B0014 V008:是version产品的大版本。 R006:是release产品特性版本。 C009:是通用版 B0014:是build开发过程中的构建版本2.硬件要求 #安全版和企业版 内存:1GB 以上 硬盘…...

深度学习之模型压缩三驾马车:模型剪枝、模型量化、知识蒸馏
一、引言 在深度学习中,我们训练出的神经网络往往非常庞大(比如像 ResNet、YOLOv8、Vision Transformer),虽然精度很高,但“太重”了,运行起来很慢,占用内存大,不适合部署到手机、摄…...
