深入剖析:基于红黑树实现自定义 map 和 set 容器
🌟 快来参与讨论💬,点赞👍、收藏⭐、分享📤,共创活力社区。🌟

在 C++ 标准模板库(STL)的大家庭里,map和set可是超级重要的关联容器成员呢😎!它们凭借红黑树这一强大的数据结构,实现了查找、插入和删除等操作的高效运行。
现在,就让我们一步步深入探索如何亲手基于红黑树打造自定义的map和set容器吧🧐!
目录
深入剖析:基于红黑树实现自定义 map 和 set 容器 🚀
一、红黑树基础结构与操作 🌳
1. 红黑树节点结构 📄
2. 红黑树类基本框架 📐
3. 左旋操作 🔄
4. 右旋操作 🔄
5. 插入修复 🔧
6. 插入操作 📥
7. 查找操作 🔍
8. 红黑树析构函数 🗑️
二、自定义 map 和 set 实现 🛠️
1. 自定义 set 实现 📚
(1)SetKeyOfT 仿函数 📐
2. 自定义 map 实现 🗺️
(1)MapKeyOfT 仿函数 📐
三、测试代码 🧪
一、红黑树基础结构与操作 🌳
1. 红黑树节点结构 📄
红黑树的节点结构包含节点颜色、父节点指针、左右子节点指针以及存储的数据。
- 实现思路:定义一个结构体来表示红黑树的节点,包含节点颜色、父节点指针、左右子节点指针和存储的数据。为方便后续操作,节点默认颜色设为红色,新插入节点通常为红色,有助于维持红黑树性质。
- 代码实现:
// 定义红黑树节点颜色
enum Colour {RED,BLACK
};// 红黑树节点结构体
template<class T>
class RBTreeNode {
public:RBTreeNode(const T& data) : _data(data),_left(nullptr),_right(nullptr),_parent(nullptr),_col(RED){}RBTreeNode<T>* _left;RBTreeNode<T>* _right;RBTreeNode<T>* _parent;Colour _col;T _data;
};
2. 红黑树类基本框架 📐
- 实现思路:定义红黑树类,包含根节点指针。提供插入、查找等基本操作函数声明,用于数据的插入、检索;同时定义左旋、右旋等内部操作函数声明,用于调整树结构,维持红黑树性质。
- 代码实现:
template<class K, class T, class KeyOfT>
class RBTree {
public:typedef RBTreeNode<T> Node;typedef _TreeIterator<T, T&, T*> iterator;typedef _TreeIterator<T, const T&, const T*> const_iterator;iterator begin();iterator end();const_iterator begin() const;const_iterator end() const;pair<Node*, bool> insert(const T& data);private:Node* _root = nullptr;void RotateL(Node* parent);void RotateR(Node* parent);void RotateRL(Node* parent);void RotateLR(Node* parent);
};
3. 左旋操作 🔄

实现步骤👇
-
保存关键节点指针:
- 保存
parent的右子节点subR和subR的左子节点subRL。
- 保存
-
调整
parent的右子节点:- 将
parent的右子节点更新为subRL。 - 如果
subRL不为空,将subRL的父节点指针指向parent。
- 将
-
调整
subR的左子节点:- 将
subR的左子节点更新为parent。 - 保存
parent的父节点parentParent。 - 将
parent的父节点指针指向subR。
- 将
-
更新根节点或父节点的子节点指针:
- 如果
parent是根节点(即parentParent为空),将subR设为新的根节点,并将subR的父节点指针置为空。 - 否则,根据
parent是parentParent的左子节点还是右子节点,更新parentParent的相应子节点指针为subR,并将subR的父节点指针指向parentParent。
- 如果
代码实现:
template<class K, class T, class KeyOfT>
void RBTree<K, T, KeyOfT>::RotateL(Node* parent) { Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL) {subRL->_parent = parent;}subR->_left = parent;Node* parentParent = parent->_parent;parent->_parent = subR;if (parentParent == nullptr) {_root = subR;subR->_parent = nullptr;}else {if (parentParent->_left == parent) {parentParent->_left = subR;}else {parentParent->_right = subR;}subR->_parent = parentParent;}
}
4. 右旋操作 🔄
- 实现思路:右旋操作以
parent为中心,交换其与左子节点subL位置,调整subLR指针,更新根或父节点指向维持平衡 - 代码实现:
template<class K, class T, class KeyOfT>
void RBTree<K, T, KeyOfT>::RotateR(Node* parent) { Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subL->_right;if (subLR) {subLR->_parent = parent;}subL->_right = parent;Node* parentParent = parent->_parent;parent->_parent = subL;if (parentParent == nullptr) {_root = subL;subL->_parent = nullptr;}else {if (parentParent->_left == parent) {parentParent->_left = subL;}else {parentParent->_right = subL;}subL->_parent = parentParent;}
}
5. 插入修复 🔧
- 实现思路:插入新节点后,红黑树的性质可能会被破坏,需要进行修复操作。修复操作主要根据新节点的父节点和叔节点的颜色进行分类处理,通过旋转和颜色调整来恢复红黑树的性质。
- 代码实现:
pair<Node*,bool> insert(const T& data)
{if (_root == nullptr){_root = new Node(data);_root->_col = BLACK;return make_pair(_root, true);}Node* cur = _root;Node* parent = nullptr;KeyOfT kot;while (cur){parent = cur;if (kot(cur->_data) < kot(data)){cur = cur->_right;}else if (kot(cur->_data) > kot(data)){cur = cur->_left;}else{return make_pair(cur, false);}}//新增结点给红色cur = new Node(data);Node* newNode = cur;cur->_parent = parent;if (kot(parent->_data) < kot(cur->_data)){parent->_right = cur;}else{parent->_left = cur;}while (parent && parent->_col == RED){//找叔叔Node* grandfather = parent->_parent;Node* uncle = nullptr;if (parent == grandfather->_left){uncle = grandfather->_right;}else{uncle = grandfather->_left;}if (uncle && uncle->_col == RED)//满足规则一,父亲和叔叔变黑,爷爷变红{parent->_col = uncle->_col = BLACK;grandfather->_col = RED;//继续向上更新cur = grandfather;parent = grandfather->_parent;}else //叔叔 不存在 或 存在且为黑{if (parent == grandfather->_left && cur == parent->_left)//右单旋{RotateR(grandfather);//变色parent->_col = BLACK;grandfather->_col = RED;}else if (parent == grandfather->_right && cur == parent->_right)//左单旋{RotateL(grandfather);//变色parent->_col = BLACK;grandfather->_col = RED;}else if (parent == grandfather->_left && cur == parent->_right)//折射,双旋{RotateLR(grandfather);//变色cur->_col = BLACK;grandfather->_col = RED;}else if (parent == grandfather->_right && cur == parent->_left)//折射,双旋{RotateRL(grandfather);//变色cur->_col = BLACK;grandfather->_col = RED;}}}_root->_col = BLACK;return make_pair(newNode, true);
}
6. 插入操作 📥
- 实现思路:首先找到合适的插入位置,创建新节点并插入到树中,然后调用插入修复函数来恢复红黑树的性质。
- 代码实现:
template<class K, class T, class KeyOfT>
pair<typename RBTree<K, T, KeyOfT>::Node*, bool> RBTree<K, T, KeyOfT>::insert(const T& data) {if (_root == nullptr) {_root = new Node(data);_root->_col = BLACK;return make_pair(_root, true);}Node* cur = _root;Node* parent = nullptr;KeyOfT kot;while (cur) {parent = cur;if (kot(cur->_data) < kot(data)) {cur = cur->_right;}else if (kot(cur->_data) > kot(data)) {cur = cur->_left;}else {return make_pair(cur, false);}}// 插入新节点并设置颜色cur = new Node(data);Node* newNode = cur;cur->_parent = parent;if (kot(parent->_data) < kot(cur->_data)) {parent->_right = cur;}else {parent->_left = cur;}while (parent && parent->_col == RED) {// 情况分类Node* grandfather = parent->_parent;Node* uncle = nullptr;if (parent == grandfather->_left) {uncle = grandfather->_right;}else {uncle = grandfather->_left;}if (uncle && uncle->_col == RED) { // 叔叔节点存在且为红色parent->_col = uncle->_col = BLACK;grandfather->_col = RED;// 继续向上调整cur = grandfather;parent = grandfather->_parent;}else { // 叔叔节点不存在或为黑色if (parent == grandfather->_left && cur == parent->_left) { // 左左情况RotateR(grandfather);// 调整颜色parent->_col = BLACK;grandfather->_col = RED;}else if (parent == grandfather->_right && cur == parent->_right) { // 右右情况RotateL(grandfather);// 调整颜色parent->_col = BLACK;grandfather->_col = RED;}else if (parent == grandfather->_left && cur == parent->_right) { // 左右情况RotateLR(grandfather);// 调整颜色cur->_col = BLACK;grandfather->_col = RED;}else if (parent == grandfather->_right && cur == parent->_left) { // 右左情况RotateRL(grandfather);// 调整颜色cur->_col = BLACK;grandfather->_col = RED;}}}_root->_col = BLACK;return make_pair(newNode, true);
}
7. 查找操作 🔍
- 实现思路:从根节点开始,根据键的大小比较,递归地在左子树或右子树中查找目标节点。
- 代码实现:
template<class K, class T, class KeyOfT>
RBTreeNode<T>* RBTree<K, T, KeyOfT>::Find(const K& key) {RBTreeNode<T>* current = _root;KeyOfT kot;while (current) {if (key < kot(current->_data)) {current = current->_left;}else if (key > kot(current->_data)) {current = current->_right;}else {return current;}}return nullptr;
}
8. 红黑树析构函数 🗑️
- 实现思路:采用后序遍历的方式递归删除树中的所有节点,释放内存。
- 代码实现:
template<class K, class T, class KeyOfT>
RBTree<K, T, KeyOfT>::~RBTree() {auto destroyTree = [](RBTreeNode<T>* node) {if (node != nullptr) {destroyTree(node->left);destroyTree(node->right);delete node;}};destroyTree(_root);
}
二、自定义 map 和 set 实现 🛠️
1. 自定义 set 实现 📚
(1)SetKeyOfT 仿函数 📐
- 实现思路:由于
set中存储的元素就是键,因此仿函数直接返回元素本身。 - 代码实现:
namespace zdf {template<class K>class set {public:struct SetKeyOfT {const K& operator()(const K& key) {return key;}};// 定义迭代器类型typedef typename RBTree<K, K, SetKeyOfT>::const_iterator iterator;typedef typename RBTree<K, K, SetKeyOfT>::const_iterator const_iterator;iterator begin() const {return _t.begin();}iterator end() const {return _t.end();}pair<iterator, bool> insert(const K& key) {return _t.insert(key);}private:RBTree<K, K, SetKeyOfT> _t;};
}
2. 自定义 map 实现 🗺️
(1)MapKeyOfT 仿函数 📐
- 实现思路:
map中存储的是键值对,仿函数从键值对中提取键。 - 代码实现:
namespace zdf {template<class K, class V>class map {struct MapKeyOfT {const K& operator()(const std::pair<K, V>& kv) {return kv.first;}};public:typedef typename RBTree<K, std::pair<const K, V>, MapKeyOfT>::iterator iterator;typedef typename RBTree<K, std::pair<const K, V>, MapKeyOfT>::const_iterator const_iterator;iterator begin() {return _t.begin();}iterator end() {return _t.end();}V& operator[](const K& key) {std::pair<iterator, bool> ret = insert(std::make_pair(key, V()));return ret.first->second;}pair<iterator, bool> insert(const std::pair<K, V>& kv) {return _t.insert(kv);}private:RBTree<K, std::pair<const K, V>, MapKeyOfT> _t;};
}
三、测试代码 🧪
#include <iostream>int main() {// 测试setzdf::set<int> s;s.insert(3);s.insert(1);s.insert(2);// 测试mapzdf::map<int, std::string> m;m.insert({ 1, "one" });m.insert({ 2, "two" });m[3] = "three";std::cout << "Map value at key 3: " << m[3] << std::endl;return 0;
}

通过以上步骤,我们基于红黑树实现了自定义的map和set容器,每个函数的实现思路和代码都进行了详细讲解。这些实现展示了红黑树在关联容器中的重要应用,以及如何通过封装和扩展红黑树来实现高效的数据存储和操作。 🎉
欢迎关注我 👉【A charmer】

相关文章:

深入剖析:基于红黑树实现自定义 map 和 set 容器
🌟 快来参与讨论💬,点赞👍、收藏⭐、分享📤,共创活力社区。🌟 在 C 标准模板库(STL)的大家庭里,map和set可是超级重要的关联容器成员呢😎&#x…...

在大数据项目中如何设计和优化数据模型
在大数据项目中,设计和优化数据模型是一个涉及多个步骤和维度的复杂过程。以下是我通常采取的方法: 一、数据模型设计 明确业务需求: 深入了解项目的业务场景和目标,明确数据模型需要解决的具体问题。与业务团队紧密合作…...
、querySelectorAll() CSS选择器解析(DOM元素选择))
JavaScript querySelector()、querySelectorAll() CSS选择器解析(DOM元素选择)
文章目录 基于querySelector系列方法的CSS选择器深度解析一、方法概述二、基础选择器类型1. 类型选择器2. ID选择器3. 类选择器4. 属性选择器 三、组合选择器1. 后代组合器2. 子元素组合器3. 相邻兄弟组合器4. 通用兄弟组合器 四、伪类与伪元素1. 结构伪类2. 状态伪类3. 内容伪…...

Linux系统中处理子进程的终止问题
1. 理解子进程终止的机制 在Unix/Linux系统中,当子进程终止时,会向父进程发送一个SIGCHLD信号。父进程需要捕捉这个信号,并通过调用wait()或waitpid()等函数来回收子进程的资源。这一过程被称为“回收僵尸进程”。 如果父进程没有及时调用w…...

Docker 不再难懂:快速掌握容器命令与架构原理
1. Docker 是容器技术的一种 容器(Container)概述 容器(Container)是一种轻量级的虚拟化技术,它将应用程序及其所有依赖环境打包在一个独立的、可移植的运行时环境中。容器通过操作系统级的虚拟化提供隔离࿰…...

取消票证会把指定的票证从数据库中删除,同时也会把票证和航班 等相关表中的关联关系一起删除。但在删除之前,它会先检查当前用户是否拥有这张票
在做航班智能客服问答系统时会遇到取消票证的场景,这里涉及数据库的操作时会把指定的票证从数据库中删除,同时也会把票证和航班等相关表中的关联关系一起删除。但在删除之前,需要先检查当前用户是否拥有这张票,只有票主才有权限取…...

力扣-贪心-763 划分字母区间
思路 先统计字符串中每一个字母出现的最后下标,然后从end初始化为第一个字母出现的最后下标,在i<end时,不断更新end,因为一旦囊括新的字母就最起码要遍历到新字母出现的最后下标,在i>end时,说明遍历…...

【Redis 原理】网络模型
文章目录 用户空间 && 内核空间阻塞IO非阻塞IO信号驱动IO异步IOIO多路复用selectpollepoll Web服务流程Redis 网络模型Redis单线程网络模型的整个流程Redis多线程网络模型的整个流程 用户空间 && 内核空间 为了避免用户应用导致冲突甚至内核崩溃,用…...

cpp中的继承
一、继承概念 在cpp中,封装、继承、多态是面向对象的三大特性。这里的继承就是允许已经存在的类(也就是基类)的基础上创建新类(派生类或者子类),从而实现代码的复用。 如上图所示,Person是基类&…...

DeepSeek全栈接入指南:从零到生产环境的深度实践
第一章:DeepSeek技术体系全景解析 1.1 认知DeepSeek技术生态 DeepSeek作为新一代人工智能技术平台,构建了覆盖算法开发、模型训练、服务部署的全链路技术栈。其核心能力体现在: 1.1.1 多模态智能引擎 自然语言处理:支持文本生成(NLG)、语义理解(NLU)、情感分析等计算…...

CSS 真的会阻塞文档解析吗?
在网页开发领域,一个常见的疑问是 CSS 是否会阻塞文档解析。理解这一问题对于优化网页性能、提升用户体验至关重要。要深入解答这个问题,需要从浏览器渲染网页的原理说起。 浏览器渲染网页的基本流程 浏览器在接收到 HTML 文档后,会依次进行…...
大模型的UI自动化:Cline 使用Playwright MCP Server完成测试
大模型的UI自动化:Cline 使用Playwright MCP Server完成测试 MCP MCP(Model Context Protocol),是一个开发的协议,标准化了应用程序如何为大模型提供上下文。MCP提供了一个标准的为LLM提供数据、工具的方式,使用MCP会更容易的构建Agent或者是基于LLM的复杂工作流。 最近…...
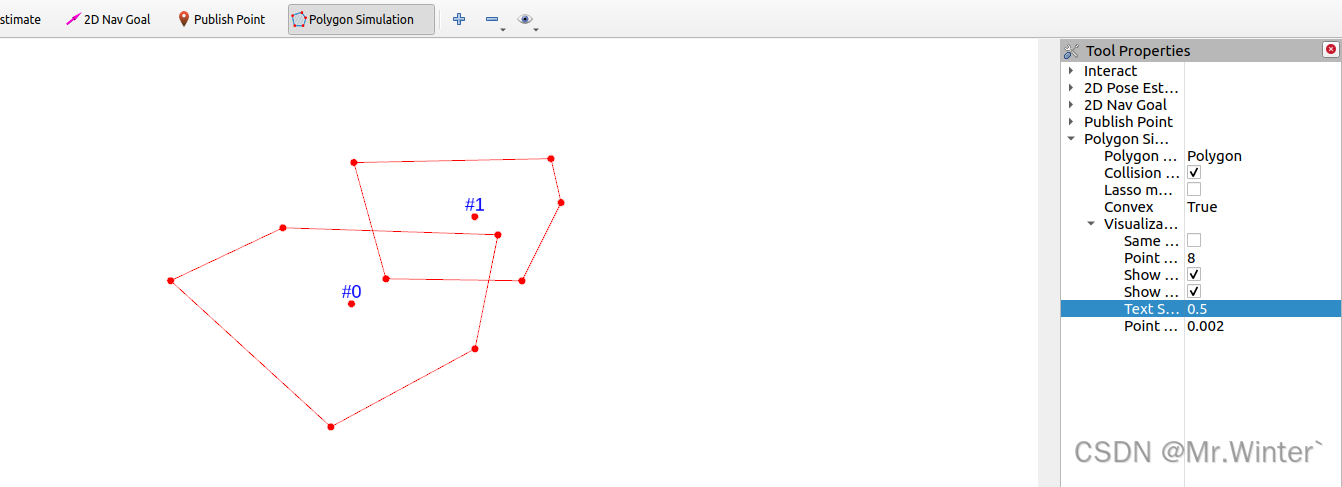
碰撞检测 | 图解凸多边形分离轴定理(附ROS C++可视化)
目录 0 专栏介绍1 凸多边形碰撞检测2 多边形判凸算法3 分离轴定理(SAT)4 算法仿真与可视化4.1 核心算法4.2 仿真实验 0 专栏介绍 🔥课设、毕设、创新竞赛必备!🔥本专栏涉及更高阶的运动规划算法轨迹优化实战,包括:曲线…...

Python 基本数据类型
目录 1. 字符串(String) 2. 列表(List) 3. 字典(Dictionary) 4. 集合(Set) 5. 数字(Number) 6. 布尔值(Boolean) 1. 字符串&…...

突破“第一崇拜“:五维心理重构之路
一、视频介绍 在这个崇尚"第一"的时代,我们如何找到自己的独特价值?本视频将带您踏上五维心理重构之旅,从诗意人生的角度探讨如何突破"圣人之下皆蝼蚁"的局限。我们将穿越人生的不同阶段,从青春的意气风发到…...

KubeKey一键安装部署k8s集群和KubeSphere详细教程
目录 一、KubeKey简介 二、k8s集群KubeSphere安装 集群规划 硬件要求 Kubernetes支持版本 操作系统要求 SSH免密登录 配置集群时钟 所有节点安装依赖 安装docker DNS要求 存储要求 下载 KubeKey 验证KubeKey 配置集群文件 安装集群 验证命令 登录页面 一、Ku…...

UE5网络通信架构解析
文章目录 前言一、客户端-服务器架构(C/S Model)二、对等网络架构(P2P,非原生支持)三、混合架构(自定义扩展)四、UE5网络核心机制 前言 UE5的网络通信主要基于客户端-服务器(C/S&am…...

实验3 知识表示与推理
实验3 知识表示与推理 一、实验目的 (1)掌握知识和知识表示的基本概念,理解其在AI中的深刻含义与意义; (2)熟悉AI中常用的知识表示方法的优缺点及其应用场景; (3)掌握产…...

基于Springboot银行信用卡额度管理系统【附源码】
基于Springboot银行信用卡额度管理系统 效果如下: 系统登陆页面 用户个人中心页面 新增信用卡申请页面 评估审核页面 管理员主页面 评估审核页面 操作日志管理页面 消费页面 研究背景 随着金融行业的快速发展和信息技术的不断进步,信用卡作为一种便捷…...

达梦数据库学习笔记@1
目录 达梦数据库学习笔记一、表空间管理(一)默认表空间(二)相关数据字典(三)表空间操作(四)临时表空间管理 二、重做日志管理(一)系统视图(二&…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

并发编程 - go版
1.并发编程基础概念 进程和线程 A. 进程是程序在操作系统中的一次执行过程,系统进行资源分配和调度的一个独立单位。B. 线程是进程的一个执行实体,是CPU调度和分派的基本单位,它是比进程更小的能独立运行的基本单位。C.一个进程可以创建和撤销多个线程;同一个进程中…...
