数学建模之数学模型—2:非线性规划
文章目录
非线性规划
基本概念与结论
有约束非线性规划的一般数学模型为如下形式:
min f ( x ) s . t . { g i ( x ) ⩾ 0 , i = 1 , 2 , . . . , m h j ( x ) = 0 , j = 1 , 2 , . . . , n \min f\left( x \right) \\ s.t.\left\{ \begin{array}{c} g_i\left( x \right) \geqslant 0,i=1,2,...,m\\ h_j\left( x \right) =0,j=1,2,...,n\\ \end{array} \right. minf(x)s.t.{gi(x)⩾0,i=1,2,...,mhj(x)=0,j=1,2,...,n
下面给出非线性规划的基本概念
定义1:设 f ( x ) f(x) f(x)为目标函数, S S S为可行域, x ∗ ∈ S x^*\in S x∗∈S。若: ∀ x ∈ S , f ( x ) ⩾ f ( x ∗ ) \forall x\in S,f\left( x \right) \geqslant f\left( x^* \right) ∀x∈S,f(x)⩾f(x∗)则称 x ∗ x^{*} x∗为
min f ( x ) s . t . x ∈ S \min f\left( x \right) \\ s.t. x\in S minf(x)s.t.x∈S
极小化问题的最优解(全局最优解)。
定义2:设 f ( x ) f(x) f(x)为目标函数, S S S为可行域, x ∗ ∈ S x^*\in S x∗∈S。若: ∃ x ∗ ∈ { x ∣ ∥ x − x ∗ ∥ < ε , ε > 0 } , f ( x ) ⩾ f ( x ∗ ) \exist x^*\in \left\{ x\left| \left\| x-x^* \right\| \right. <\varepsilon ,\varepsilon >0 \right\} ,f\left( x \right) \geqslant f\left( x^* \right) ∃x∗∈{x∣∥x−x∗∥<ε,ε>0},f(x)⩾f(x∗)则称 x ∗ x^{*} x∗为极小化问题:
min f ( x ) s . t . x ∈ S \min f\left( x \right) \\ s.t. x\in S minf(x)s.t.x∈S
的局部最优解。
凸集与凸函数
定义:设 f : S ⊂ R n → R f:S\subset R^{n}\rightarrow R f:S⊂Rn→R, S S S是凸集,如果对所有的 x ( 1 ) , x ( 2 ) ∈ S x^{(1)},x^{(2)}\in S x(1),x(2)∈S, λ ∈ ( 0 , 1 ) \lambda\in(0,1) λ∈(0,1),都有: f ( λ x ( 1 ) + ( 1 − λ ) x ( 2 ) ) ⩽ λ f ( x ( 1 ) ) + ( 1 − λ ) f ( x ( 2 ) ) f(\lambda x^{(1)}+(1-\lambda )x^{(2)})\leqslant \lambda f( x^{(1)})+(1-\lambda )f(x^{(2)}) f(λx(1)+(1−λ)x(2))⩽λf(x(1))+(1−λ)f(x(2))
称 f ( x ) f(x) f(x)为 S S S上的凸函数。
Hessian矩阵: f f f存在二阶偏导数, x ∈ R n x\in R^{n} x∈Rn: ∇ 2 f ( x ) = ( ∂ 2 f ( x ) ∂ x 1 2 ∂ 2 f ( x ) ∂ x 1 ∂ x 2 . . . ∂ 2 f ( x ) ∂ x 1 ∂ x n ∂ 2 f ( x ) ∂ x 2 ∂ x 1 ∂ 2 f ( x ) ∂ x 2 2 . . . ∂ 2 f ( x ) ∂ x 2 ∂ x n ⋮ ⋮ ⋱ ⋮ ∂ 2 f ( x ) ∂ x n ∂ x 1 ∂ 2 f ( x ) ∂ x n ∂ x 2 . . . ∂ 2 f ( x ) ∂ x n 2 ) \nabla ^2f\left( x \right) =\left( \begin{matrix} \frac{\partial ^2f\left( x \right)}{\partial x_{1}^{2}}& \frac{\partial ^2f\left( x \right)}{\partial x_1\partial x_2}& ...& \frac{\partial ^2f\left( x \right)}{\partial x_1\partial x_n}\\ \frac{\partial ^2f\left( x \right)}{\partial x_2\partial x_1}& \frac{\partial ^2f\left( x \right)}{\partial x_{2}^{2}}& ...& \frac{\partial ^2f\left( x \right)}{\partial x_2\partial x_n}\\ \vdots& \vdots& \ddots& \vdots\\ \frac{\partial ^2f\left( x \right)}{\partial x_n\partial x_1}& \frac{\partial ^2f\left( x \right)}{\partial x_n\partial x_2}& ...& \frac{\partial ^2f\left( x \right)}{\partial x_{n}^{2}}\\ \end{matrix} \right) ∇2f(x)= ∂x12∂2f(x)∂x2∂x1∂2f(x)⋮∂xn∂x1∂2f(x)∂x1∂x2∂2f(x)∂x22∂2f(x)⋮∂xn∂x2∂2f(x)......⋱...∂x1∂xn∂2f(x)∂x2∂xn∂2f(x)⋮∂xn2∂2f(x)
下面给出一系列定理:
- 定理1:有限凸函数的线性组合为凸函数
- 定理2:凸函数在有限函数值处的沿任意方向导数都存在
- 定理3:凸函数在定义区间上必连续
- 定理4:设 S S S是 R n R^{n} Rn上的非空凸集, f ( x ) f(x) f(x)是定义在 S S S上的凸函数,则 f ( x ) f(x) f(x)在 S S S上的局限极小点是全局极小点,且极小点的集合为凸集
- 凸函数的一阶、二阶判断定理:
- ∃ x ( 1 ) ≠ x ( 2 ) ∈ S ≠ ⊘ , S 是一个凸集, f 可微 : f 为凸函数 ⇔ f ( x ( 2 ) ) ⩾ f ( x ( 1 ) ) + ∇ f ( x ( 1 ) ) T ( x ( 2 ) − x ( 1 ) ) \exists x^{\left( 1 \right)}\ne x^{\left( 2 \right)}\in S\ne \oslash ,S\text{是一个凸集,}f\text{可微}:f\text{为凸函数}\Leftrightarrow f\left( x^{\left( 2 \right)} \right) \geqslant f\left( x^{\left( 1 \right)} \right) +\nabla f\left( x^{\left( 1 \right)} \right) ^T\left( x^{\left( 2 \right)}-x^{\left( 1 \right)} \right) ∃x(1)=x(2)∈S=⊘,S是一个凸集,f可微:f为凸函数⇔f(x(2))⩾f(x(1))+∇f(x(1))T(x(2)−x(1))
- 在凸集定义内的点的
Hessian矩阵半正定 ⇔ \Leftrightarrow ⇔凸函数 - 在凸集定义上所有的点在其处的
Hessian矩阵正定 ⇒ \Rightarrow ⇒严格凸函数
凸规划
min f ( x ) s . t . { g i ( x ) ⩾ 0 , i = 1 , 2 , . . . , m h j ( x ) = 0 , j = 1 , 2 , . . . , n \min f\left( x \right) \\ s.t.\left\{ \begin{array}{c} g_i\left( x \right) \geqslant 0,i=1,2,...,m\\ h_j\left( x \right) =0,j=1,2,...,n\\ \end{array} \right. minf(x)s.t.{gi(x)⩾0,i=1,2,...,mhj(x)=0,j=1,2,...,n
f ( x ) f\left( x \right) f(x)为凸函数, g i ( x ) g_i\left( x \right) gi(x)为凹函数, h j ( x ) h_j\left( x \right) hj(x)为线性函数,称此类问题为凸规划
极值条件
无约束条件的极值判断条件
无约束非线性规划的一般数学模型为如下形式: min f ( x ) x ∈ R n \min f\left( x \right) \\ x\in \mathbb{R} ^n minf(x)x∈Rn
定理1: 设函数 f ( x ) 在 x ‾ 处可微 , 若存在向量 d , 使得 ∇ f ( x ‾ ) T d < 0 , 则存在数 δ > 0 , 使得对 ∀ λ ∈ ( 0 , δ ) , 有 f ( x ‾ + λ d ) < f ( x ‾ ) \text{设函数}f\left( x \right) \text{在}\overline{x}\text{处可微},\text{若存在向量}d,\text{使得}\nabla f\left( \overline{x} \right) ^Td<0,\text{则存在数}\delta >0,\text{使得对}\forall \lambda \in \left( 0,\delta \right) ,\text{有}f\left( \overline{x}+\lambda d \right) <f\left( \overline{x} \right) 设函数f(x)在x处可微,若存在向量d,使得∇f(x)Td<0,则存在数δ>0,使得对∀λ∈(0,δ),有f(x+λd)<f(x)
定理2: 设函数 f ( x ) 在点 x ‾ 处可微,若 x ‾ 是局部最小点 , 则 ∇ f ( x ‾ ) = 0 \text{设函数}f\left( x \right) \text{在点}\overline{x}\text{处可微,若}\overline{x}\text{是局部最小点},\text{则}\nabla f\left( \overline{x} \right) =0 设函数f(x)在点x处可微,若x是局部最小点,则∇f(x)=0
定理3: 设函数 f ( x ) 在点 x ‾ 处二次可微 , 若 x ‾ 是局部极小点,则 ∇ f ( x ‾ ) = 0 , 且 ∇ 2 f ( x ‾ ) 半正定 \text{设函数}f\left( x \right) \text{在点}\overline{x}\text{处二次可微},\text{若}\overline{x}\text{是局部极小点,则}\nabla f\left( \overline{x} \right) =0,\text{且}\nabla ^2f\left( \overline{x} \right) \text{半正定} 设函数f(x)在点x处二次可微,若x是局部极小点,则∇f(x)=0,且∇2f(x)半正定
定理4——局部极小点: 设函数 f ( x ) 在点 x ‾ 处二次可微 , 若 ∇ f ( x ‾ ) = 0 , 且 ∇ 2 f ( x ‾ ) 正定,则 x ‾ 是局部极小点 \text{设函数}f\left( x \right) \text{在点}\overline{x}\text{处二次可微},\text{若}\nabla f\left( \overline{x} \right) =0,\text{且}\nabla ^2f\left( \overline{x} \right) \text{正定,则}\overline{x}\text{是局部极小点} 设函数f(x)在点x处二次可微,若∇f(x)=0,且∇2f(x)正定,则x是局部极小点
定理5——全局最小点: 设函数 f ( x ) 在 R n 上的可微函数 , x ‾ ∈ R n , 则 x ‾ 是全局极小点 ⇔ ∇ f ( x ‾ ) = 0 \text{设函数}f\left( x \right) \text{在}R^n\text{上的可微函数},\overline{x}\in R^n,\text{则}\overline{x}\text{是全局极小点}\Leftrightarrow \nabla f\left( \overline{x} \right) =0 设函数f(x)在Rn上的可微函数,x∈Rn,则x是全局极小点⇔∇f(x)=0
有约束条件的极值判断条件
有约束非线性规划的一般数学模型为如下表现形式:
min f ( x ) s . t . { g i ( x ) ⩾ 0 , i = 1 , 2 , . . . , m h j ( x ) = 0 , j = 1 , 2 , . . . , n \min f\left( x \right) \\ s.t.\left\{ \begin{array}{c} g_i\left( x \right) \geqslant 0,i=1,2,...,m\\ h_j\left( x \right) =0,j=1,2,...,n\\ \end{array} \right. minf(x)s.t.{gi(x)⩾0,i=1,2,...,mhj(x)=0,j=1,2,...,n
其中 x ∈ R n x\in R^n x∈Rn, f ( x ) f(x) f(x), g i ( x ) g_i(x) gi(x), h j ( x ) h_j(x) hj(x)都是定义在 R n R^n Rn上的实值函数。
FRitz John条件——一般约束的一阶必要条件:
x ‾ 为可行点 , I = { i ∣ g i ( x ‾ ) = 0 } , f 和 g i ( x ‾ ) ( i ∈ I ) 在点 x ‾ 处可微 , g i ( x ‾ ) ( i ∉ I ) 在点 x ‾ 处连续, h j ( x ) ( j = 1 , 2 , . . . , l ) 在点 x ‾ 处连续可微。如果 x ‾ 是局部最优解 , 则存在不全为 0 的数 u 0 , u i ( i ∈ I ) 和 v j ( j = 1 , 2 , . . . , l ) , 使得: u 0 ∇ f ( x ‾ ) + ∑ i ∈ I u i ∇ g i ( x ∗ ) − ∑ j = 1 l μ j ∇ h j ( x ∗ ) = 0 , u 0 , u i ⩾ 0 \overline{x}\text{为可行点},I=\left\{ i|g_i\left( \overline{x} \right) =0 \right\} ,f\text{和}g_i\left( \overline{x} \right) \left( i\in I \right) \text{在点}\overline{x}\text{处可微},g_i\left( \overline{x} \right) \left( i\notin I \right) \text{在点}\overline{x}\text{处连续,}h_j\left( x \right) \left( j=1,2,...,l \right) \text{在点}\overline{x}\text{处连续可微。如果}\overline{x}\text{是局部最优解},\text{则存在不全为}0\text{的数}u_0,u_i\left( i\in I \right) \text{和}v_j\left( j=1,2,...,l \right) ,\text{使得:} \\ u_0\nabla f(\overline{x})+\sum_{i\in I}^{}{u_i\nabla g_i(x^*)}-\sum_{j=1}^l{\mu _j\nabla h_j(x^*)}=0, u_0,u_i\geqslant 0 x为可行点,I={i∣gi(x)=0},f和gi(x)(i∈I)在点x处可微,gi(x)(i∈/I)在点x处连续,hj(x)(j=1,2,...,l)在点x处连续可微。如果x是局部最优解,则存在不全为0的数u0,ui(i∈I)和vj(j=1,2,...,l),使得:u0∇f(x)+i∈I∑ui∇gi(x∗)−j=1∑lμj∇hj(x∗)=0,u0,ui⩾0
无约束非线性规划
一维搜索
一维搜索又称直线搜索,是指单变量函数最优化,即求一维问题的最优解方法,这里介绍黄金分割法
- 先在区间 [ a , b ] \left[ a,b \right] [a,b]上插入两个试探点: t l = a + ( 1 − β ) ( b − a ) , t r = a + β ( b − a ) t_l=a+\left( 1-\beta \right) \left( b-a \right) ,t_r=a+\beta \left( b-a \right) tl=a+(1−β)(b−a),tr=a+β(b−a)
- 由单峰函数性质丢掉 1 3 \frac{1}{3} 31区间,逐步搜索
黄金分割法是一维搜索中用于求解单变量函数最优解的一种高效方法,以下是对它更详细的介绍:
算法步骤
- 初始化
- 给定初始搜索区间 [ a , b ] [a,b] [a,b],以及精度要求 ϵ \epsilon ϵ。
- 计算试探点
- 计算两个试探点: t l = a + ( 1 − β ) ( b − a ) t_l=a+(1 - \beta)(b - a) tl=a+(1−β)(b−a), t r = a + β ( b − a ) t_r=a+\beta(b - a) tr=a+β(b−a)。
- 比较函数值
- 计算 f ( t l ) f(t_l) f(tl)和 f ( t r ) f(t_r) f(tr),比较它们的大小。
- 若 f ( t l ) < f ( t r ) f(t_l)<f(t_r) f(tl)<f(tr),则新的搜索区间为 [ a , t r ] [a,t_r] [a,tr]。
- 若 f ( t l ) ≥ f ( t r ) f(t_l)\geq f(t_r) f(tl)≥f(tr),则新的搜索区间为 [ t l , b ] [t_l,b] [tl,b]。
- 判断终止条件
- 检查新的搜索区间长度是否小于精度要求 ϵ \epsilon ϵ,即 ∣ b − a ∣ < ϵ |b - a|<\epsilon ∣b−a∣<ϵ。
- 若是,则取当前区间的中点或两个试探点中函数值较好的点作为近似最优解,算法结束。
- 若否,则返回步骤2,继续迭代。
示例
假设要求函数 f ( x ) = − x 2 + 4 x − 3 f(x)=-x^2 + 4x - 3 f(x)=−x2+4x−3在区间 [ 0 , 4 ] [0,4] [0,4]上的最大值。
- 首先,初始化 a = 0 a = 0 a=0, b = 4 b = 4 b=4, β = 0.618 \beta = 0.618 β=0.618。
- 计算试探点:
- t l = 0 + ( 1 − 0.618 ) × ( 4 − 0 ) = 1.528 t_l=0+(1 - 0.618)\times(4 - 0)=1.528 tl=0+(1−0.618)×(4−0)=1.528。
- t r = 0 + 0.618 × ( 4 − 0 ) = 2.472 t_r=0+0.618\times(4 - 0)=2.472 tr=0+0.618×(4−0)=2.472。
- 计算函数值:
- f ( t l ) = f ( 1.528 ) = − 1.52 8 2 + 4 × 1.528 − 3 = 1.315 f(t_l)=f(1.528)=-1.528^2 + 4\times1.528 - 3=1.315 f(tl)=f(1.528)=−1.5282+4×1.528−3=1.315。
- f ( t r ) = f ( 2.472 ) = − 2.47 2 2 + 4 × 2.472 − 3 = 1.985 f(t_r)=f(2.472)=-2.472^2 + 4\times2.472 - 3=1.985 f(tr)=f(2.472)=−2.4722+4×2.472−3=1.985。
- 因为 f ( t l ) < f ( t r ) f(t_l)<f(t_r) f(tl)<f(tr),所以新的搜索区间为 [ 0 , 2.472 ] [0,2.472] [0,2.472]。
- 继续迭代,直到满足精度要求。
特点
- 优点
- 不需要计算函数的导数,适用于导数不存在或难以计算的函数。
- 算法简单,易于实现。
- 收敛速度较快,每次迭代都能将搜索区间缩小一定比例。
- 缺点
- 对于非单峰函数可能无法找到全局最优解。
- 收敛速度相对较慢,与一些基于导数的方法相比,需要更多的迭代次数才能达到相同的精度。
代码模板
import math# 定义黄金分割比
GOLDEN_RATIO = (math.sqrt(5) - 1) / 2def golden_section_search(func, a, b, epsilon=1e-6):"""黄金分割法进行一维搜索:param func: 目标函数:param a: 搜索区间左端点:param b: 搜索区间右端点:param epsilon: 精度要求:return: 近似最优解"""# 计算初始试探点t_l = a + (1 - GOLDEN_RATIO) * (b - a)t_r = a + GOLDEN_RATIO * (b - a)# 计算初始试探点的函数值f_l = func(t_l)f_r = func(t_r)while (b - a) > epsilon:if f_l < f_r:# 新的搜索区间为 [a, t_r]b = t_rt_r = t_lf_r = f_lt_l = a + (1 - GOLDEN_RATIO) * (b - a)f_l = func(t_l)else:# 新的搜索区间为 [t_l, b]a = t_lt_l = t_rf_l = f_rt_r = a + GOLDEN_RATIO * (b - a)f_r = func(t_r)# 返回近似最优解return (a + b) / 2# 示例目标函数
def example_function(x):return -x**2 + 4*x - 3# 测试代码
if __name__ == "__main__":a = 0b = 4result = golden_section_search(example_function, a, b)print(f"近似最优解: {result}")print(f"最优解处的函数值: {example_function(result)}")
最速下降法
最速下降法属于迭代算法。求解无约束非线性规划的迭代算法一般具有如下形式
- 选定初始点 x ( 0 ) , k = 0 x^{(0)},k=0 x(0),k=0
- k = k + 1 k=k+1 k=k+1
- 寻找一个合适的方向 P ( k ) P^{(k)} P(k)
- 求出沿着这个方向的前进步长 λ ( k ) \lambda^{(k)} λ(k)
- 得到新的点 x ( k + 1 ) = x ( k ) + λ ( k ) P ( k ) x^{(k+1)}=x^{(k)}+\lambda^{(k)}P^{(k)} x(k+1)=x(k)+λ(k)P(k)
最速下降算法的基本思想是沿着负梯度方向搜索极值点,即搜索方向:
P ( k ) = − ∇ f ( x ( k ) ) P^{(k)}=-\nabla f(x^{(k)}) P(k)=−∇f(x(k))
搜索步长满足以下条件:
f ( x ( k ) + λ ( k ) P ( k ) ) = m i n λ ⩾ 0 f ( x ( k ) − λ ∇ f ( x ( k ) ) ) f(x^{(k)}+\lambda ^{(k)}P^{(k)})=\underset{\lambda\geqslant 0 }{min}f(x^{(k)}-\lambda \nabla f(x^{(k)})) f(x(k)+λ(k)P(k))=λ⩾0minf(x(k)−λ∇f(x(k)))
算法详细步骤
- 初始化
选定初始点 x ( 0 ) x^{(0)} x(0),并令迭代计数器 k = 0 k = 0 k=0。初始点的选择通常会影响算法的收敛速度和最终结果,在实际应用中,可以根据问题的特点或经验来选择合适的初始点。 - 迭代过程
- 步骤一:更新迭代计数器
- k = k + 1 k=k + 1 k=k+1
- 步骤二:确定搜索方向
- 计算当前点 x ( k ) x^{(k)} x(k) 处目标函数 f ( x ) f(x) f(x) 的梯度 ∇ f ( x ( k ) ) \nabla f(x^{(k)}) ∇f(x(k)),搜索方向 P ( k ) P^{(k)} P(k) 取为负梯度方向,即 P ( k ) = − ∇ f ( x ( k ) ) P^{(k)}=-\nabla f(x^{(k)}) P(k)=−∇f(x(k))。梯度 ∇ f ( x ) \nabla f(x) ∇f(x) 是一个向量,它的每个分量是目标函数关于各个变量的偏导数。
- 步骤三:确定搜索步长
- 搜索步长 λ ( k ) \lambda^{(k)} λ(k) 要满足 f ( x ( k ) + λ ( k ) P ( k ) ) = m i n λ ⩾ 0 f ( x ( k ) − λ ∇ f ( x ( k ) ) ) f(x^{(k)}+\lambda ^{(k)}P^{(k)})=\underset{\lambda\geqslant 0 }{min}f(x^{(k)}-\lambda \nabla f(x^{(k)})) f(x(k)+λ(k)P(k))=λ⩾0minf(x(k)−λ∇f(x(k)))。这意味着要在负梯度方向上找到一个最优的步长,使得目标函数值下降最多。在实际计算中,精确求解这个一维搜索问题可能比较困难,因此常常采用一些近似的方法,如黄金分割法、斐波那契法等进行一维搜索来确定步长。
- 步骤四:更新迭代点
- 得到新的点 x ( k + 1 ) = x ( k ) + λ ( k ) P ( k ) x^{(k + 1)}=x^{(k)}+\lambda^{(k)}P^{(k)} x(k+1)=x(k)+λ(k)P(k)。
- 终止条件
可以根据不同的准则来判断迭代是否终止,常见的终止条件有:
- 梯度的模小于某个给定的小正数 ϵ \epsilon ϵ,即 ∥ ∇ f ( x ( k ) ) ∥ < ϵ \left\|\nabla f(x^{(k)})\right\|<\epsilon ∇f(x(k)) <ϵ。这表示目标函数在当前点的变化率已经很小,可能已经接近极值点。
- 相邻两次迭代点的距离小于某个给定的小正数 ϵ \epsilon ϵ,即 ∥ x ( k + 1 ) − x ( k ) ∥ < ϵ \left\|x^{(k + 1)}-x^{(k)}\right\|<\epsilon x(k+1)−x(k) <ϵ。
- 目标函数值的变化小于某个给定的小正数 ϵ \epsilon ϵ,即 ∣ f ( x ( k + 1 ) ) − f ( x ( k ) ) ∣ < ϵ \left|f(x^{(k + 1)})-f(x^{(k)})\right|<\epsilon f(x(k+1))−f(x(k)) <ϵ。
代码实现示例
import numpy as np
import math# 定义黄金分割比
GOLDEN_RATIO = (math.sqrt(5) - 1) / 2# 黄金分割法进行一维搜索
def golden_section_search(func, a=0, b=10, epsilon=1e-6):t_l = a + (1 - GOLDEN_RATIO) * (b - a)t_r = a + GOLDEN_RATIO * (b - a)f_l = func(t_l)f_r = func(t_r)while (b - a) > epsilon:if f_l < f_r:b = t_rt_r = t_lf_r = f_lt_l = a + (1 - GOLDEN_RATIO) * (b - a)f_l = func(t_l)else:a = t_lt_l = t_rf_l = f_rt_r = a + GOLDEN_RATIO * (b - a)f_r = func(t_r)return (a + b) / 2# 最速下降法
def steepest_descent(f, grad_f, x0, epsilon=1e-6, max_iter=1000):"""最速下降法求解无约束非线性规划问题:param f: 目标函数:param grad_f: 目标函数的梯度函数:param x0: 初始点:param epsilon: 收敛精度:param max_iter: 最大迭代次数:return: 最优解"""x = np.array(x0, dtype=np.float64)k = 0while k < max_iter:# 计算当前点的梯度grad = grad_f(x)# 判断是否满足收敛条件if np.linalg.norm(grad) < epsilon:break# 确定搜索方向,为负梯度方向p = -grad# 定义一维搜索的目标函数def one_dim_func(lambda_):return f(x + lambda_ * p)# 使用黄金分割法确定步长lambda_ = golden_section_search(one_dim_func)# 更新迭代点x = x + lambda_ * pk += 1return x# 示例目标函数
def example_f(x):"""示例目标函数:f(x) = x1^2 + x2^2"""return np.sum(np.square(x))# 示例目标函数的梯度
def example_grad_f(x):"""示例目标函数的梯度:grad f(x) = [2*x1, 2*x2]"""return 2 * x# 主程序
if __name__ == "__main__":# 初始点x0 = [1.0, 1.0]# 调用最速下降法求解result = steepest_descent(example_f, example_grad_f, x0)print("最优解:", result)print("最优值:", example_f(result))
最优步长的求解
以下是使用黄金分割法和斐波那契法求步长 λ ( k ) \lambda^{(k)} λ(k)的具体方法:
黄金分割法
- 原理
- 黄金分割法是基于黄金分割比例来逐步缩小搜索区间,以逼近函数的最优解。对于一个单峰函数,在搜索区间 [ a , b ] [a,b] [a,b]内,通过在两个特定点 x 1 x_1 x1和 x 2 x_2 x2处计算函数值,根据函数值的大小关系,不断舍弃不包含最优解的区间,从而使搜索区间不断缩小。
- 这两个特定点 x 1 x_1 x1和 x 2 x_2 x2与区间端点的距离满足黄金分割比例,即 x 1 − a b − a = b − x 2 b − a = 5 − 1 2 ≈ 0.618 \frac{x_1 - a}{b - a}=\frac{b - x_2}{b - a}=\frac{\sqrt{5}-1}{2}\approx0.618 b−ax1−a=b−ab−x2=25−1≈0.618。
- 计算步骤
- 首先确定初始搜索区间 [ a , b ] [a,b] [a,b],即确定步长 λ \lambda λ的取值范围,保证目标函数 f ( x ( k ) + λ P ( k ) ) f(x^{(k)}+\lambda P^{(k)}) f(x(k)+λP(k))在该区间内是单峰的。
- 计算区间内的两个试探点 x 1 = a + 0.382 ( b − a ) x_1 = a + 0.382(b - a) x1=a+0.382(b−a), x 2 = a + 0.618 ( b − a ) x_2 = a + 0.618(b - a) x2=a+0.618(b−a),并计算对应的函数值 f 1 = f ( x ( k ) + x 1 P ( k ) ) f_1 = f(x^{(k)}+x_1 P^{(k)}) f1=f(x(k)+x1P(k)), f 2 = f ( x ( k ) + x 2 P ( k ) ) f_2 = f(x^{(k)}+x_2 P^{(k)}) f2=f(x(k)+x2P(k))。
- 比较 f 1 f_1 f1和 f 2 f_2 f2的大小,如果 f 1 < f 2 f_1 < f_2 f1<f2,则新的搜索区间为 [ a , x 2 ] [a,x_2] [a,x2];否则,新的搜索区间为 [ x 1 , b ] [x_1,b] [x1,b]。
- 重复上述步骤,不断缩小搜索区间,直到满足预设的精度要求,此时的区间中点或其中一个端点即可作为近似的最优步长 λ ( k ) \lambda^{(k)} λ(k)。
斐波那契法
- 原理
- 斐波那契法也是一种用于一维搜索的区间收缩方法,它与黄金分割法类似,但在确定试探点的位置时,是根据斐波那契数列来确定的。斐波那契数列满足 F n = F n − 1 + F n − 2 F_n = F_{n - 1}+F_{n - 2} Fn=Fn−1+Fn−2,其中 F 0 = 0 F_0 = 0 F0=0, F 1 = 1 F_1 = 1 F1=1。
- 在搜索过程中,利用斐波那契数列的性质来确定试探点的位置,使得在给定的搜索次数下,能够最大程度地缩小搜索区间。
- 计算步骤
- 同样先确定初始搜索区间 [ a , b ] [a,b] [a,b]和搜索次数 n n n。
- 根据斐波那契数列计算出第 n n n项 F n F_n Fn以及前一项 F n − 1 F_{n - 1} Fn−1,第一个试探点为 x 1 = a + F n − 1 F n ( b − a ) x_1 = a+\frac{F_{n - 1}}{F_n}(b - a) x1=a+FnFn−1(b−a),第二个试探点为 x 2 = a + F n − 2 F n ( b − a ) x_2 = a+\frac{F_{n - 2}}{F_n}(b - a) x2=a+FnFn−2(b−a),计算对应的函数值 f 1 = f ( x ( k ) + x 1 P ( k ) ) f_1 = f(x^{(k)}+x_1 P^{(k)}) f1=f(x(k)+x1P(k)), f 2 = f ( x ( k ) + x 2 P ( k ) ) f_2 = f(x^{(k)}+x_2 P^{(k)}) f2=f(x(k)+x2P(k))。
- 比较 f 1 f_1 f1和 f 2 f_2 f2的大小,根据大小关系舍弃相应的区间,更新搜索区间和试探点。
- 随着搜索次数的增加,不断重复上述步骤,当达到预定的搜索次数 n n n时,得到的搜索区间的中点或其中一个端点就是近似的最优步长 λ ( k ) \lambda^{(k)} λ(k)。
牛顿法
牛顿法基本思想以目标函数的一个二次函数作为其近似,然后求出这个二次函数的极小值点,从而该极小值点近似为原目标函数的一个局部极小值点。
设 f ( x ) f(x) f(x)是二次可微函数。假设上一步迭代到了 x ( k ) x^{(k)} x(k)。我们在点 x ( k ) x^{(k)} x(k)处 T a y l o r Taylor Taylor展开,取二阶近似:
f ( x ) ≈ Q ( x ) = f ( x ( k ) ) + ∇ f ( x ( k ) ) T ( x − x ( k ) ) + 1 2 ( x − x ( k ) ) T ∇ 2 f ( x ( k ) ) ( x − x ( k ) ) f\left( x \right) \approx Q\left( x \right) =f\left( x^{\left( k \right)} \right) +\nabla f\left( x^{\left( k \right)} \right) ^T\left( x-x^{\left( k \right)} \right) +\frac{1}{2}\left( x-x^{\left( k \right)} \right) ^T\nabla ^2f\left( x^{\left( k \right)} \right) \left( x-x^{\left( k \right)} \right) f(x)≈Q(x)=f(x(k))+∇f(x(k))T(x−x(k))+21(x−x(k))T∇2f(x(k))(x−x(k))
g ( x ( k ) ) = Δ ∇ f ( x ( k ) ) , H ( x ( k ) ) = Δ ∇ 2 f ( x ( k ) ) g\left( x^{\left( k \right)} \right) \overset{\varDelta}{=}\nabla f\left( x^{\left( k \right)} \right) ,H\left( x^{\left( k \right)} \right) \overset{\varDelta}{=}\nabla ^2f\left( x^{\left( k \right)} \right) g(x(k))=Δ∇f(x(k)),H(x(k))=Δ∇2f(x(k))
反解可得到:
x = x ( k ) − ∇ 2 f ( x ( k ) ) − 1 ∇ f ( x ( k ) ) x=x^{\left( k \right)}-\nabla ^2f\left( x^{\left( k \right)} \right) ^{-1}\nabla f\left( x^{\left( k \right)} \right) x=x(k)−∇2f(x(k))−1∇f(x(k))
基于上面给出的信息,我们得到牛顿算法:
(1)给定初始点 x ( 1 ) ∈ R n x^{\left( 1 \right)}\in R^n x(1)∈Rn,给定误差 ϵ > 0 \epsilon>0 ϵ>0,令 k = 1 k=1 k=1
(2)由 ∇ 2 f ( x ( k ) ) d ( k ) = − ∇ f ( x ( k ) ) \nabla ^2f\left( x^{\left( k \right)} \right) d^{\left( k \right)}=-\nabla f\left( x^{\left( k \right)} \right) ∇2f(x(k))d(k)=−∇f(x(k)),解线性方程组得到搜索方向 d ( k ) d^{(k)} d(k)
(3)置 x ( k + 1 ) = x ( k ) + d ( k ) x^{\left( k+1 \right)}=x^{\left( k \right)}+d^{\left( k \right)} x(k+1)=x(k)+d(k),即 x ( k + 1 ) = x ( k ) − ∇ 2 f ( x ( k ) ) − 1 ∇ f ( x ( k ) ) x^{(k+1)}=x^{\left( k \right)}-\nabla ^2f\left( x^{\left( k \right)} \right) ^{-1}\nabla f\left( x^{\left( k \right)} \right) x(k+1)=x(k)−∇2f(x(k))−1∇f(x(k))
(4)当 ∥ d ( k ) ∥ < ϵ \left\| d^{\left( k \right)} \right\| <\epsilon d(k) <ϵ,迭代终止,否则, k = k + 1 k=k+1 k=k+1,跳转到 2 2 2
import numpy as npdef newton_method(f, grad_f, hess_f, x1, epsilon=1e-6, max_iter=100):"""牛顿算法实现参数:f: 目标函数grad_f: 目标函数的梯度hess_f: 目标函数的海森矩阵x1: 初始点,numpy 数组epsilon: 误差阈值,默认为 1e-6max_iter: 最大迭代次数,默认为 100返回:x: 最优解iter_count: 迭代次数"""x = x1.copy()k = 0while k < max_iter:# 步骤 2: 求解线性方程组得到搜索方向grad = grad_f(x)hess = hess_f(x)try:# 解线性方程组 H * d = -gradd = np.linalg.solve(hess, -grad)except np.linalg.LinAlgError:print("海森矩阵不可逆,无法求解线性方程组。")break# 步骤 3: 更新 xx_new = x + d# 步骤 4: 判断是否满足终止条件if np.linalg.norm(d) < epsilon:breakx = x_newk += 1return x, k# 示例:定义一个简单的目标函数及其梯度和海森矩阵
def f(x):# 目标函数 f(x) = x1^2 + x2^2return x[0]**2 + x[1]**2def grad_f(x):# 目标函数的梯度return np.array([2 * x[0], 2 * x[1]])def hess_f(x):# 目标函数的海森矩阵return np.array([[2, 0], [0, 2]])# 初始点
x1 = np.array([1.0, 1.0])# 调用牛顿算法
optimal_x, iter_count = newton_method(f, grad_f, hess_f, x1)print("最优解:", optimal_x)
print("迭代次数:", iter_count)
阻尼牛顿法
阻尼牛顿法与原始牛顿法的主要区别在于增加了沿着牛顿方向进行一维搜索,其迭代公式:
x ( k + 1 ) = x ( k ) + λ ( k ) d ( k ) x^{\left( k+1 \right)}=x^{\left( k \right)}+\lambda ^{\left( k \right)}d^{\left( k \right)} x(k+1)=x(k)+λ(k)d(k)
-
(1)给定初始点 x ( 1 ) ∈ R n x^{\left( 1 \right)}\in R^n x(1)∈Rn,给定误差 ϵ > 0 \epsilon>0 ϵ>0,令 k = 1 k=1 k=1
-
(2)由 ∇ 2 f ( x ( k ) ) d ( k ) = − ∇ f ( x ( k ) ) \nabla ^2f\left( x^{\left( k \right)} \right) d^{\left( k \right)}=-\nabla f\left( x^{\left( k \right)} \right) ∇2f(x(k))d(k)=−∇f(x(k)),解线性方程组得到搜索方向 d ( k ) d^{(k)} d(k)
-
(3) 从 x ( k ) x^{(k)} x(k)出发,沿着 d ( k ) d^{(k)} d(k)方向一维搜索: min λ f ( x ( k ) + λ d ( k ) ) \underset{\lambda}{\min}\,\,f\left( x^{\left( k \right)}+\lambda d^{\left( k \right)} \right) λminf(x(k)+λd(k))
-
(4)置 x ( k + 1 ) = x ( k ) + d ( k ) x^{\left( k+1 \right)}=x^{\left( k \right)}+d^{\left( k \right)} x(k+1)=x(k)+d(k),即 x ( k + 1 ) = x ( k ) − λ ( k ) ∇ 2 f ( x ( k ) ) − 1 ∇ f ( x ( k ) ) x^{(k+1)}=x^{\left( k \right)}-\lambda ^{\left( k \right)}\nabla ^2f\left( x^{\left( k \right)} \right) ^{-1}\nabla f\left( x^{\left( k \right)} \right) x(k+1)=x(k)−λ(k)∇2f(x(k))−1∇f(x(k))
-
(5)当 ∥ d ( k ) ∥ < ϵ \left\| d^{\left( k \right)} \right\| <\epsilon d(k) <ϵ,迭代终止,否则, k = k + 1 k=k+1 k=k+1,跳转到 2 2 2
模式搜索法
Powell方法
Powell方法是研究对称正定的二次函数:
f ( x ) = 1 2 x T Q x + b T x + c f(x)=\frac{1}{2}x^TQx+b^Tx+c f(x)=21xTQx+bTx+c
极小化问题时候形成的。
- (1)选定初始点 x ( 0 ) x^{\left( 0 \right)} x(0), n n n个线性无关向量 d ( i ) d^{(i)} d(i),,给定误差 ϵ > 0 \epsilon>0 ϵ>0,令 k = 1 k=1 k=1, i = 1 , 2 , . . . , n i=1,2,...,n i=1,2,...,n
- (2)依次对目标函数作直线搜索 { f ( x ( i − 1 ) + λ i d ( i ) ) = min λ ∈ R f ( x ( i − 1 ) + λ d ( i ) ) x ( i ) = x ( i − 1 ) + λ i d ( i ) \left\{ \begin{array}{c} f\left( x^{\left( i-1 \right)}+\lambda _id^{\left( i \right)} \right) =\underset{\lambda \in R}{\min}f\left( x^{\left( i-1 \right)}+\lambda d^{\left( i \right)} \right)\\ x^{\left( i \right)}=x^{\left( i-1 \right)}+\lambda _id^{\left( i \right)}\\ \end{array} \right. {f(x(i−1)+λid(i))=λ∈Rminf(x(i−1)+λd(i))x(i)=x(i−1)+λid(i)
- (3) 对 i = 1 , 2 , . . . , n − 1 i=1,2,...,n-1 i=1,2,...,n−1, d ( i ) = d ( i + 1 ) d^{(i)}=d^{(i+1)} d(i)=d(i+1), d ( n + 1 ) = x ( n ) − x ( 0 ) d^{(n+1)}=x^{(n)}-x^{(0)} d(n+1)=x(n)−x(0),置 d ( n ) = d ( n + 1 ) d^{(n)}=d^{(n+1)} d(n)=d(n+1)
- (4)直线搜索 x ( n + 1 ) = x ( n ) + λ n + 1 d ( n + 1 ) x^{\left( n+1 \right)}=x^{\left( n \right)}+\lambda _{n+1}d^{\left( n+1 \right)} x(n+1)=x(n)+λn+1d(n+1), f ( x ( n ) + λ n + 1 d ( n + 1 ) ) = min f ( x ( n ) + λ d ( n + 1 ) ) f\left( x^{\left( n \right)}+\lambda _{n+1}d^{\left( n+1 \right)} \right) =\min f\left( x^{\left( n \right)}+\lambda d^{\left( n+1 \right)} \right) f(x(n)+λn+1d(n+1))=minf(x(n)+λd(n+1))
- (5) ∥ x ( n + 1 ) − x ( 0 ) ∥ < ϵ , x ( n + 1 ) \left\| x^{\left( n+1 \right)}-x^{\left( 0 \right)} \right\| <\epsilon ,x^{\left( n+1 \right)} x(n+1)−x(0) <ϵ,x(n+1)就是所求的极小值点,则停止计算,否则转第 6 6 6步
- (6)置 x ( 0 ) = x ( n + 1 ) x^{(0)}=x^{(n+1)} x(0)=x(n+1)转 ( 2 ) (2) (2)
有约束非线性规划
有约束非线性规划的一般数学模型为如下形式:
min f ( x ) s . t . { g i ( x ) ⩾ 0 , i = 1 , 2 , . . . , m h j ( x ) = 0 , j = 1 , 2 , . . . , n \min f\left( x \right) \\ s.t.\left\{ \begin{array}{c} g_i\left( x \right) \geqslant 0,i=1,2,...,m\\ h_j\left( x \right) =0,j=1,2,...,n\\ \end{array} \right. minf(x)s.t.{gi(x)⩾0,i=1,2,...,mhj(x)=0,j=1,2,...,n
其中 f ( x ) , g i ( x ) , h i ( x ) f(x),g_{i}(x),h_{i}(x) f(x),gi(x),hi(x)至少有一个非线性函数。
外点罚函数法
外点罚函数法是一种将有约束优化问题转化为无约束优化问题的方法。其核心思想是通过在目标函数中添加一个罚项,当约束条件不满足时,罚项的值会变得很大,从而迫使无约束优化问题的解逐渐逼近原约束优化问题的可行域。
- 对于只含等式约束的优化问题:
min f ( x ) s . t . h j ( x ) = 0 , j = 1 , 2 , . . . , l \min f\left( x \right) \\ s.t. h_j\left( x \right) =0,j=1,2,...,l\\ minf(x)s.t.hj(x)=0,j=1,2,...,l
采用如下方法建立罚函数:
F ( x , m k ) = f ( x ) + m k ∑ j = 1 l h j 2 ( x ) F\left( x,m_k \right) =f\left( x \right) +m_k\sum_{j=1}^l{h_{j}^{2}\left( x \right)} F(x,mk)=f(x)+mkj=1∑lhj2(x)
这样,我们就把原约束问题化为如下的无约束问题:
m i n F ( x , m k ) min F(x,m_k) minF(x,mk) - 对于不等式条件:
构造罚函数:
F ( x , m k ) = f ( x ) + m k ∑ i = 1 m g i 2 ( x ) u i ( g i ) , u 为单位跃阶函数 F\left( x,m_k \right) =f\left( x \right) +m_k\sum_{i=1}^m{g_{i}^{2}\left( x \right) u_i\left( g_i \right)},u\text{为单位跃阶函数} F(x,mk)=f(x)+mki=1∑mgi2(x)ui(gi),u为单位跃阶函数 - 综合以上思想,我们可以处理一般的罚函数
对于包含等式约束 h j ( x ) = 0 h_j(x) = 0 hj(x)=0( j = 1 , 2 , ⋯ , l j = 1, 2, \cdots, l j=1,2,⋯,l)和不等式约束 g i ( x ) ≤ 0 g_i(x) \leq 0 gi(x)≤0( i = 1 , 2 , ⋯ , m i = 1, 2, \cdots, m i=1,2,⋯,m)的一般约束优化问题:
min f ( x ) s.t. h j ( x ) = 0 , j = 1 , 2 , ⋯ , l g i ( x ) ≤ 0 , i = 1 , 2 , ⋯ , m \begin{align*} \min &\quad f(x) \\ \text{s.t.} &\quad h_j(x) = 0, \quad j = 1, 2, \cdots, l \\ &\quad g_i(x) \leq 0, \quad i = 1, 2, \cdots, m \end{align*} mins.t.f(x)hj(x)=0,j=1,2,⋯,lgi(x)≤0,i=1,2,⋯,m
可以构造外点罚函数:
F ( x , m k ) = f ( x ) + m k ( ∑ j = 1 l h j 2 ( x ) + ∑ i = 1 m [ max { 0 , g i ( x ) } ] 2 ) F(x, m_k) = f(x) + m_k \left( \sum_{j = 1}^l h_j^2(x) + \sum_{i = 1}^m [\max\{0, g_i(x)\}]^2 \right) F(x,mk)=f(x)+mk(j=1∑lhj2(x)+i=1∑m[max{0,gi(x)}]2)
其中, m k m_k mk 是罚因子,且满足 0 < m 1 < m 2 < ⋯ < m k < ⋯ 0 < m_1 < m_2 < \cdots < m_k < \cdots 0<m1<m2<⋯<mk<⋯, lim k → ∞ m k = ∞ \lim_{k \to \infty} m_k = \infty limk→∞mk=∞。
算法步骤
- 初始化:选择初始点 x ( 0 ) x^{(0)} x(0),初始罚因子 m 1 > 0 m_1 > 0 m1>0,罚因子增长系数 c > 1 c > 1 c>1,收敛精度 ϵ > 0 \epsilon > 0 ϵ>0,令 k = 1 k = 1 k=1。
- 求解无约束优化问题:以 x ( k − 1 ) x^{(k - 1)} x(k−1) 为初始点,求解无约束优化问题 min F ( x , m k ) \min F(x, m_k) minF(x,mk),得到最优解 x ( k ) x^{(k)} x(k)。
- 判断收敛条件:如果满足 ∣ F ( x ( k ) , m k ) − F ( x ( k − 1 ) , m k − 1 ) ∣ < ϵ \left| F(x^{(k)}, m_k) - F(x^{(k - 1)}, m_{k - 1}) \right| < \epsilon F(x(k),mk)−F(x(k−1),mk−1) <ϵ 或者约束条件的违反程度足够小(例如, ∑ j = 1 l h j 2 ( x ( k ) ) + ∑ i = 1 m [ max { 0 , g i ( x ( k ) ) } ] 2 < ϵ \sum_{j = 1}^l h_j^2(x^{(k)}) + \sum_{i = 1}^m [\max\{0, g_i(x^{(k)})\}]^2 < \epsilon ∑j=1lhj2(x(k))+∑i=1m[max{0,gi(x(k))}]2<ϵ),则停止迭代, x ( k ) x^{(k)} x(k) 即为原约束优化问题的近似最优解;否则,进入下一步。
- 更新罚因子:令 m k + 1 = c m k m_{k + 1} = c m_k mk+1=cmk, k = k + 1 k = k + 1 k=k+1,返回步骤 2。
Python 代码实现
import numpy as np
from scipy.optimize import minimizedef penalty_function(x, f, h, g, mk):"""计算外点罚函数的值:param x: 当前点:param f: 目标函数:param h: 等式约束函数列表:param g: 不等式约束函数列表:param mk: 罚因子:return: 罚函数的值"""penalty_term = 0# 等式约束的罚项for hj in h:penalty_term += hj(x) ** 2# 不等式约束的罚项for gi in g:penalty_term += max(0, gi(x)) ** 2return f(x) + mk * penalty_termdef outer_penalty_method(f, h, g, x0, m1=1.0, c=10.0, epsilon=1e-6, max_iter=100):"""外点罚函数法求解约束优化问题:param f: 目标函数:param h: 等式约束函数列表:param g: 不等式约束函数列表:param x0: 初始点:param m1: 初始罚因子:param c: 罚因子增长系数:param epsilon: 收敛精度:param max_iter: 最大迭代次数:return: 最优解"""mk = m1x = np.array(x0)for k in range(max_iter):# 定义当前罚函数def current_penalty(x):return penalty_function(x, f, h, g, mk)# 求解无约束优化问题result = minimize(current_penalty, x)x_new = result.x# 判断收敛条件if k > 0 and np.abs(current_penalty(x_new) - current_penalty(x)) < epsilon:breakx = x_new# 更新罚因子mk *= creturn x# 示例:求解一个简单的约束优化问题
# 目标函数
def f(x):return (x[0] - 1) ** 2 + (x[1] - 2.5) ** 2# 等式约束
def h1(x):return x[0] + x[1] - 3# 不等式约束
def g1(x):return -x[0] + 2def g2(x):return -x[1] + 2# 初始点
x0 = [0, 0]# 调用外点罚函数法
optimal_x = outer_penalty_method(f, [h1], [g1, g2], x0)print("最优解:", optimal_x)
注意事项
- 罚因子的增长系数 c c c 和初始罚因子 m 1 m_1 m1 的选择会影响算法的收敛速度和稳定性,需要根据具体问题进行调整。
- 无约束优化问题的求解可以使用不同的优化算法,这里使用了
scipy.optimize.minimize函数,你可以根据需要选择其他合适的算法。
内点罚函数法
内点罚函数法(Interior Point Penalty Method),也称为障碍函数法,是一种用于求解有约束优化问题的重要方法。它主要适用于只包含不等式约束的优化问题,基本思想是在可行域内部设置障碍,使得迭代点始终保持在可行域内,并且随着迭代的进行,障碍的作用逐渐减弱,从而使迭代点逼近最优解。以下将详细介绍内点罚函数法的原理、算法步骤,并给出 Python 代码示例。
原理
考虑如下只含不等式约束的优化问题:
min f ( x ) s.t. g i ( x ) ≤ 0 , i = 1 , 2 , ⋯ , m \begin{align*} \min &\quad f(x) \\ \text{s.t.} &\quad g_i(x) \leq 0, \quad i = 1, 2, \cdots, m \end{align*} mins.t.f(x)gi(x)≤0,i=1,2,⋯,m
内点罚函数法通过构造障碍函数来实现。常见的障碍函数有倒数障碍函数和对数障碍函数。
倒数障碍函数
B ( x , r k ) = f ( x ) + r k ∑ i = 1 m 1 − g i ( x ) B(x, r_k) = f(x) + r_k \sum_{i = 1}^{m} \frac{1}{-g_i(x)} B(x,rk)=f(x)+rki=1∑m−gi(x)1
对数障碍函数
B ( x , r k ) = f ( x ) − r k ∑ i = 1 m ln ( − g i ( x ) ) B(x, r_k) = f(x) - r_k \sum_{i = 1}^{m} \ln(-g_i(x)) B(x,rk)=f(x)−rki=1∑mln(−gi(x))
其中, r k r_k rk 是障碍因子,且满足 r 1 > r 2 > ⋯ > r k > ⋯ r_1 > r_2 > \cdots > r_k > \cdots r1>r2>⋯>rk>⋯, lim k → ∞ r k = 0 \lim_{k \to \infty} r_k = 0 limk→∞rk=0。当迭代点接近可行域边界时,障碍函数的值会变得很大,从而阻止迭代点越过边界。
算法步骤
- 初始化:选择一个初始可行点 x ( 0 ) x^{(0)} x(0)(即满足所有不等式约束 g i ( x ( 0 ) ) ≤ 0 g_i(x^{(0)}) \leq 0 gi(x(0))≤0, i = 1 , 2 , ⋯ , m i = 1, 2, \cdots, m i=1,2,⋯,m),初始障碍因子 r 1 > 0 r_1 > 0 r1>0,障碍因子缩减系数 c ∈ ( 0 , 1 ) c \in (0, 1) c∈(0,1),收敛精度 ϵ > 0 \epsilon > 0 ϵ>0,令 k = 1 k = 1 k=1。
- 求解无约束优化问题:以 x ( k − 1 ) x^{(k - 1)} x(k−1) 为初始点,求解无约束优化问题 min B ( x , r k ) \min B(x, r_k) minB(x,rk),得到最优解 x ( k ) x^{(k)} x(k)。
- 判断收敛条件:如果满足 ∣ r k ∑ i = 1 m 1 − g i ( x ( k ) ) ∣ < ϵ \left| r_k \sum_{i = 1}^{m} \frac{1}{-g_i(x^{(k)})} \right| < \epsilon rk∑i=1m−gi(x(k))1 <ϵ(对于倒数障碍函数)或者 ∣ − r k ∑ i = 1 m ln ( − g i ( x ( k ) ) ∣ < ϵ \left| -r_k \sum_{i = 1}^{m} \ln(-g_i(x^{(k)}) \right| < \epsilon −rk∑i=1mln(−gi(x(k)) <ϵ(对于对数障碍函数),则停止迭代, x ( k ) x^{(k)} x(k) 即为原约束优化问题的近似最优解;否则,进入下一步。
- 更新障碍因子:令 r k + 1 = c r k r_{k + 1} = c r_k rk+1=crk, k = k + 1 k = k + 1 k=k+1,返回步骤 2。
Python 代码示例(使用对数障碍函数)
import numpy as np
from scipy.optimize import minimizedef logarithmic_barrier_function(x, f, g, rk):"""计算对数障碍函数的值:param x: 当前点:param f: 目标函数:param g: 不等式约束函数列表:param rk: 障碍因子:return: 对数障碍函数的值"""barrier_term = 0for gi in g:if gi(x) >= 0:# 如果不满足不等式约束,返回一个很大的值return np.infbarrier_term += np.log(-gi(x))return f(x) - rk * barrier_termdef interior_point_method(f, g, x0, r1=1.0, c=0.1, epsilon=1e-6, max_iter=100):"""内点罚函数法求解约束优化问题:param f: 目标函数:param g: 不等式约束函数列表:param x0: 初始可行点:param r1: 初始障碍因子:param c: 障碍因子缩减系数:param epsilon: 收敛精度:param max_iter: 最大迭代次数:return: 最优解"""rk = r1x = np.array(x0)for k in range(max_iter):# 定义当前对数障碍函数def current_barrier(x):return logarithmic_barrier_function(x, f, g, rk)# 求解无约束优化问题result = minimize(current_barrier, x)x_new = result.x# 判断收敛条件barrier_term = 0for gi in g:barrier_term += np.log(-gi(x_new))if np.abs(-rk * barrier_term) < epsilon:breakx = x_new# 更新障碍因子rk *= creturn x# 示例:求解一个简单的约束优化问题
# 目标函数
def f(x):return (x[0] - 1) ** 2 + (x[1] - 2.5) ** 2# 不等式约束
def g1(x):return -x[0] + 2def g2(x):return -x[1] + 2# 初始可行点
x0 = [1, 1]# 调用内点罚函数法
optimal_x = interior_point_method(f, [g1, g2], x0)print("最优解:", optimal_x)
代码说明
logarithmic_barrier_function函数:用于计算对数障碍函数的值。如果迭代点不满足不等式约束,返回一个很大的值,以避免该点被选为最优解。interior_point_method函数:实现了内点罚函数法的主要步骤,包括初始化、求解无约束优化问题、判断收敛条件和更新障碍因子。- 示例:定义了一个简单的约束优化问题,包含两个不等式约束,调用
interior_point_method函数求解最优解。
注意事项
- 初始可行点的选择非常重要,如果选择不当,可能会导致算法无法收敛。
- 障碍因子的缩减系数 c c c 和初始障碍因子 r 1 r_1 r1 的选择会影响算法的收敛速度和稳定性,需要根据具体问题进行调整。
相关文章:

数学建模之数学模型—2:非线性规划
文章目录 非线性规划基本概念与结论凸集与凸函数极值条件无约束条件的极值判断条件有约束条件的极值判断条件 无约束非线性规划一维搜索算法步骤示例特点代码模板 最速下降法算法详细步骤 代码实现示例最优步长的求解 黄金分割法斐波那契法牛顿法阻尼牛顿法模式搜索法Powell方法…...

unity学习51:所有UI的父物体:canvas画布
目录 1 下载资源 1.1 在window / Asset store下下载一套免费的UI资源 1.2 下载,导入import 1.3 导入后在 project / Asset下面可以看到 2 画布canvas,UI的父物体 2.1 创建canvas 2.1.1 画布的下面是 event system是UI相关的事件系统 2.2 canvas…...

ctfshow做题笔记—栈溢出—pwn57~pwn60
目录 前言 一、pwn57(先了解一下简单的64位shellcode吧) 二、pwn58 三、pwn59(64位 无限制) 四、pwn60(入门难度shellcode) 前言 往前写了几道题,与shellcode有关,关于shellc…...

数据结构 1-2 线性表的链式存储-链表
1 原理 顺序表的缺点: 插入和删除移动大量元素数组的大小不好控制占用一大段连续的存储空间,造成很多碎片 链表规避了上述顺序表缺点 逻辑上相邻的两个元素在物理位置上不相邻 头结点 L:头指针 头指针:链表中第一个结点的存储…...

ArcGIS Pro进行坡度与坡向分析
在地理信息系统中,坡度分析是一项至关重要的空间分析方法,旨在精确计算地表或地形的坡度,为地形特征识别、土地资源规划、环境保护、灾害预警等领域提供科学依据。本文将详细介绍如何利用ArcGIS Pro这一强大的地理信息系统软件,进…...

My first Android application
界面元素组成: 功能代码: /*实现功能:当输入内容后,欢迎文本发生相应改变,并清除掉文本域内容当未输入任何内容时,弹出提示文本以警告用户*/val greetingText findViewById<TextView>(R.id.printer)…...

ZLMediaKi集群设置
要在集群环境中部署 ZLMediaKit,您可以按照以下步骤进行操作。ZLMediaKit 是一个高性能的流媒体服务器,支持 RTMP、RTSP、HLS 等协议。以下是一个详细的集群部署方案: ### 1. 环境准备 - **服务器**:准备多台服务器,…...

Docker基础实践与应用举例
Docker 是一个轻量级容器化平台,通过将应用及其依赖打包到容器中,实现快速部署和环境一致性。以下是 Docker 的实践与应用场景举例,结合具体操作步骤: 一、基础实践 1. 快速启动一个容器 # 运行一个Nginx容器,映射宿…...

Innovus中快速获取timing path逻辑深度的golden脚本
在实际项目中我们经常会遇到一条timing path级数特别多,可能是一两页都翻不完。此时,我们大都需要手工去数这条path上到底有哪些是设计本身的逻辑,哪些是PR工具插入的buffer和inverter。 数字IC后端手把手培训教程 | Clock Gating相关clock …...

百度AI图片助手,免费AI去水印、画质修复、画面延展以及局部替换
最近,要是你常用百度图片,可能已经发现了它新添的一个超实用功能——百度AI图片助手。但很多朋友不知道它的入口地址,我们今天给大家分享一下。 这个功能的出现,在图片编辑修改方面带来了极大便利,它涵盖了AI去水印、…...

【前端】Axios AJAX Fetch
不定期更新,建议关注收藏点赞。 目录 AxiosAJAXCORS 允许跨域请求 Fetch Axios axios 是一个基于 Promise 的 JavaScript HTTP 客户端,用于浏览器和 Node.js 中发送 HTTP 请求。它提供了一个简单的 API 来发起请求,并处理请求的结果。axios …...

测试面试题:以一个登录窗口为例,设计一下登录界面测试的思路和方法
在测试登录窗口时,可以从 表单测试、 逻辑判断和 业务流程三个方面设计测试思路和方法。以下是一个详细的测试方案: 1. 表单测试 表单测试主要关注输入框、按钮等UI元素的正确性和用户体验。 测试点: 输入框测试 用户名和密码输入框是否正常显示。输入框是否支持预期的字符类…...

Android之图片保存相册及分享图片
文章目录 前言一、效果图二、实现步骤1.引入依赖库2.二维码生成3.布局转图片保存或者分享 总结 前言 其实现在很多分享都是我们自定义的,更多的是在界面加了很多东西,然后把整个界面转成图片保存相册和分享,而且现在分享都不需要第三方&…...

EX_25/2/24
写一个三角形类,拥有私有成员 a,b,c 三条边 写好构造函数初始化 abc 以及 abc 的set get 接口 再写一个等腰三角形类,继承自三角形类 1:写好构造函数,初始化三条边 2:要求无论如何,等腰三角形类对象&#x…...

ElasticSearch公共方法封装
业务场景 1、RestClientBuilder初始化(同时支持单机与集群) 2、发送ES查询请求公共方法封装(支持sql、kql、代理访问、集群访问、鉴权支持) 3、判断ES索引是否存在(/_cat/indices/${indexName}) 4、判断ES…...

JVM之JVM的组成
Java 虚拟机(JVM)是 Java 程序的运行核心,它主要由类加载系统、运行时数据区、执行引擎和本地方法接口这几个关键部分组成。 类加载系统(Class Loading System) 类加载系统负责在程序运行时动态地将 Java 类加载到 J…...

贪心算法
int a[1000], b5, c8; swap(b, c); // 交换操作 memset(a, 0, sizeof(a)); // 初始化为0或-1 引导问题 为一个小老鼠准备了M磅的猫粮,准备去和看守仓库的猫做交易,因为仓库里有小老鼠喜欢吃的五香豆,第i个房间有J[i] 磅的五香豆…...
Linux下安装中文输入法总结
Linux下安装中文输入法总结_linux 微软拼音-CSDN博客文章浏览阅读4.2w次,点赞21次,收藏92次。众所周知,fcitx和ibus是两款很好用的Linux中文输入法框架。下面来说一下其安装方法以及会踩的坑。首先fcitx和ibus是不能共存的,两者只…...
:科技新纪元的领航者)
人工智能(AI):科技新纪元的领航者
摘要 人工智能(AI)作为当今科技领域最具变革性的力量之一,正以惊人的速度重塑着我们的世界。本文旨在全面且专业地介绍人工智能,涵盖其定义、发展历程、关键技术、应用领域、面临的挑战以及未来展望等方面,以期为读者…...

c3p0、Druid连接池+工具类 Apache-DbUtils (详解!!!)
数据库连接池是在应用程序启动时创建一定数量的数据库连接,并将这些连接存储在池中。当应用程序需要与数据库通信时,它可以向池中请求一个连接,使用完后将连接归还给池,而不是关闭连接。这样可以减少创建和关闭连接的开销…...
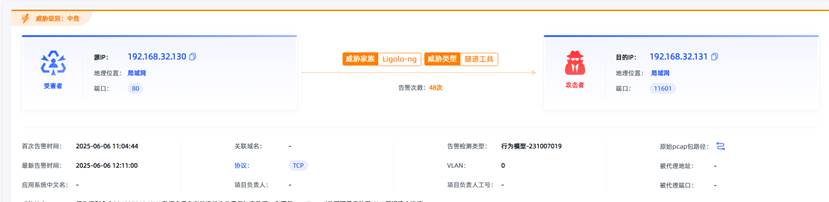
观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...
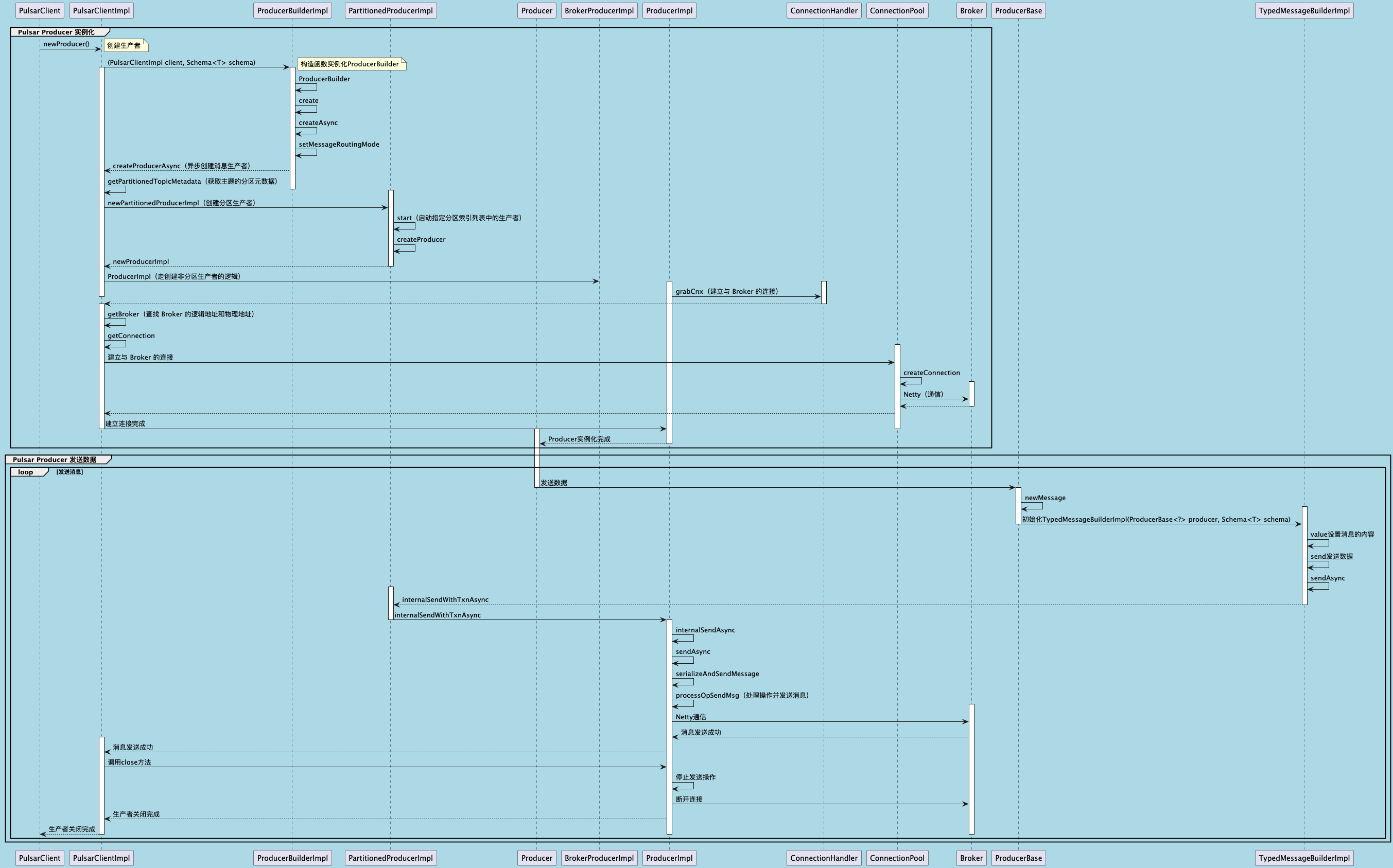
聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...
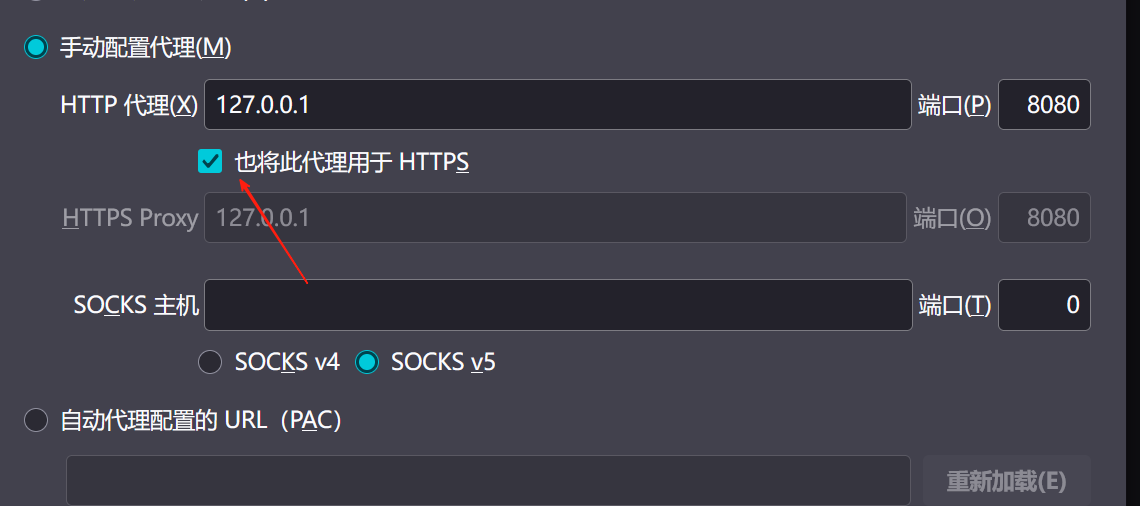
【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...
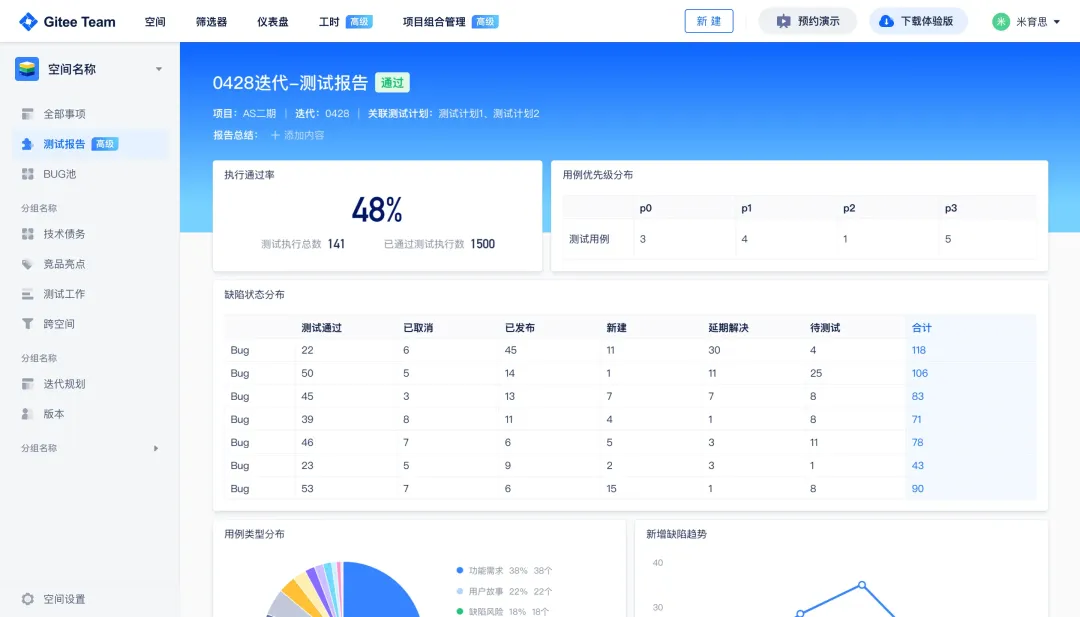
从“安全密码”到测试体系:Gitee Test 赋能关键领域软件质量保障
关键领域软件测试的"安全密码":Gitee Test如何破解行业痛点 在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的"神经中枢"。从国防军工到能源电力,从金融交易到交通管控,这些关乎国计民生的关键领域…...

在 Spring Boot 项目里,MYSQL中json类型字段使用
前言: 因为程序特殊需求导致,需要mysql数据库存储json类型数据,因此记录一下使用流程 1.java实体中新增字段 private List<User> users 2.增加mybatis-plus注解 TableField(typeHandler FastjsonTypeHandler.class) private Lis…...
