ollama无法通过IP:11434访问
目录
1.介绍
2.直接在ollama的当前命令窗口中修改(法1)
3.更改ollama配置文件(法2)
3.1更新配置
3.2重启服务
1.介绍
ollama下载后默认情况下都是直接在本地的11434端口中运行,绑定到127.0.0.1(localhost),仅允许本地访问,要想通过IP:11434访问,就要更改绑定地址为0.0.0.0
2.直接在ollama的当前命令窗口中修改(法1)
export OLLAMA_HOST=0.0.0.0:11434 #监听所有端口,解决不能通过IP访问3.更改ollama配置文件(法2)
sudo systemctl stop ollama #停止ollamasudo nano /etc/systemd/system/ollama.service #编辑环境变量
把原来的注释掉,增加新的:
Environment="OLLAMA_HOST=0.0.0.0:11434"3.1更新配置
sudo systemctl daemon-reload #更新配置3.2重启服务
sudo systemctl restart ollama #重启服务
相关文章:

ollama无法通过IP:11434访问
目录 1.介绍 2.直接在ollama的当前命令窗口中修改(法1) 3.更改ollama配置文件(法2) 3.1更新配置 3.2重启服务 1.介绍 ollama下载后默认情况下都是直接在本地的11434端口中运行,绑定到127.0.0.1(localhost)&#x…...

简单易懂,解析Go语言中的struct结构体
目录 4. struct 结构体4.1 初始化4.2 内嵌字段4.3 可见性4.4 方法与函数4.4.1 区别4.4.2 闭包 4.5 Tag 字段标签4.5.1定义4.5.2 Tag规范4.5.3 Tag意义 4. struct 结构体 go的结构体类似于其他语言中的class,主要区别就是go的结构体没有继承这一概念,但可…...
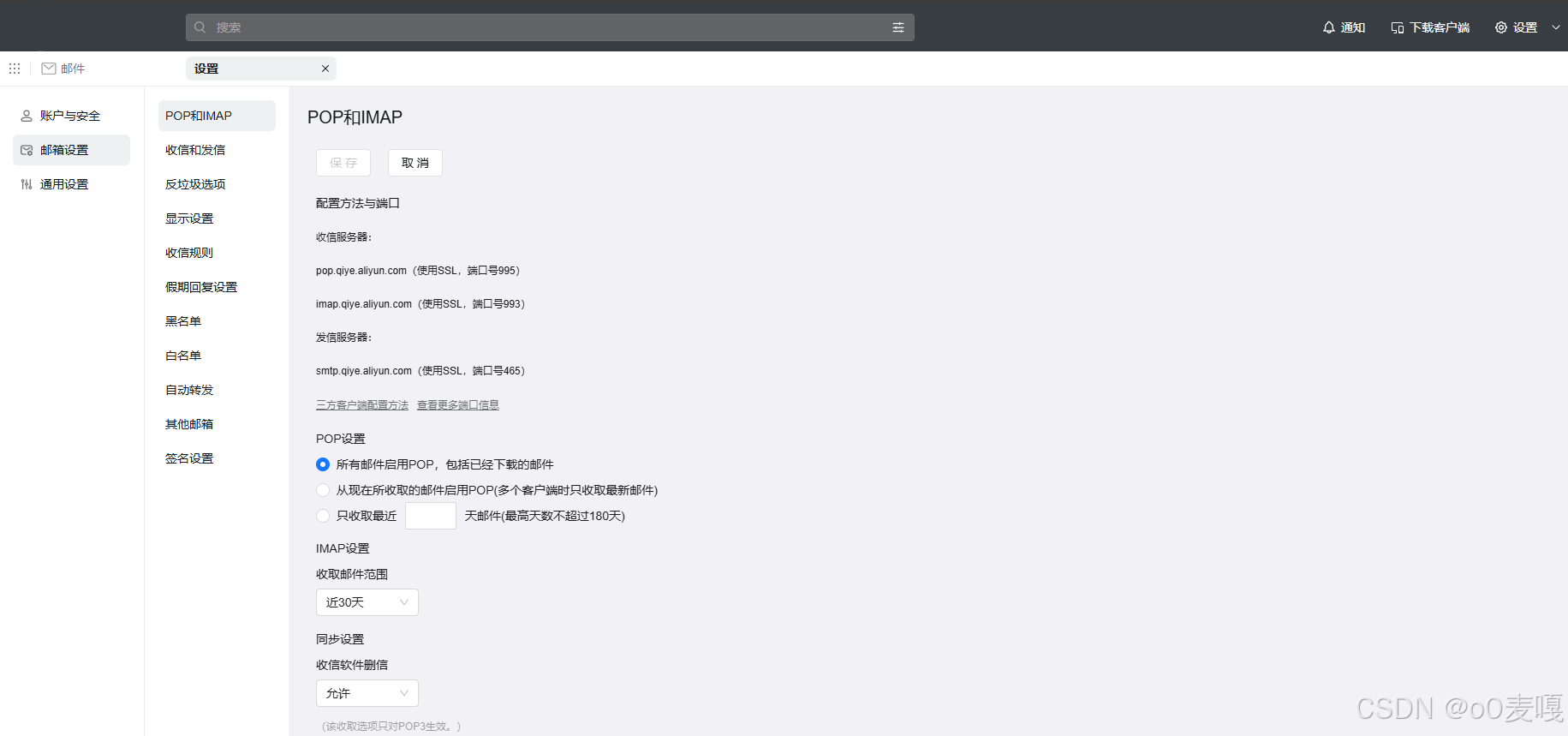
java给钉钉邮箱发送邮件
1.开通POP和IMAP 2.引入pom <dependency><groupId>javax.mail</groupId><artifactId>mail</artifactId><version>1.4.7</version> </dependency>3.逻辑 String host "smtp.qiye.aliyun.com"; String port "…...

C++和OpenGL实现3D游戏编程【连载23】——几何着色器和法线可视化
欢迎来到zhooyu的C++和OpenGL游戏专栏,专栏连载的所有精彩内容目录详见下边链接: 🔥C++和OpenGL实现3D游戏编程【总览】 1、本节实现的内容 上一节课,我们在Blend软件中导出经纬球模型时,遇到了经纬球法线导致我们在游戏中模型光照显示问题,我们在Blender软件中可以通过…...

大连本地知识库的搭建--数据收集与预处理_01
1.马蜂窝爬虫 编程语言:Python爬虫框架:Selenium(用于浏览器自动化)解析库:BeautifulSoup(用于解析HTML) 2.爬虫策略 目标网站:马蜂窝(https://www.mafengwo.cn/&…...

github 推送的常见问题以及解决
文章目录 git add 的时候问题1为什么会发生这种情况?Git 的警告含义如何解决?1. **保持 Git 的默认行为(推荐)**2. **禁用自动转换**3. **仅在工作目录中禁用转换**4. **统一使用 LF(跨平台开发推荐)** git…...

stm32单片机个人学习笔记16(SPI通信协议)
前言 本篇文章属于stm32单片机(以下简称单片机)的学习笔记,来源于B站教学视频。下面是这位up主的视频链接。本文为个人学习笔记,只能做参考,细节方面建议观看视频,肯定受益匪浅。 STM32入门教程-2023版 细…...

Linux | RHEL / CentOS 中 YUM history / downgrade 命令回滚操作
注:英文引文,机翻未校。 在 RHEL/CentOS 系统上使用 YUM history 命令回滚升级操作 作者: 2daygeek 译者: LCTT DarkSun 为服务器打补丁是 Linux 系统管理员的一项重要任务,为的是让系统更加稳定,性能更加…...

BGP状态和机制
BGP邻居优化 为了增加稳定性,通常建议实验回环口来建立邻居。更新源:建立邻居和邻居所学习到的路由的下一跳。多跳:EBGP邻居建立默认选哟直连,因为TTL=1,如果非直连,必须修改TTL。命令备注peer 2.2.2.2 connect-interface lo1配置更新源peer 2.2.2.2 ebgp-max-hop 2配置T…...

温湿度监控设备融入智慧物联网
当医院的温湿度监控设备融入智慧物联网,将会带来许多新的体验,可以帮助医院温湿度监控设备智能化管理,实现设备之间的互联互通,方便医院对温湿度数据进行统一管理和分析。 添加智慧物联网技术,实现对医院温湿度的实时…...

smolagents学习笔记系列(五)Tools-in-depth-guide
这篇文章锁定官网教程中的 Tools-in-depth-guide 章节,主要介绍了如何详细构造自己的Tools,在之前的博文 smolagents学习笔记系列(二)Agents - Guided tour 中我初步介绍了下如何将一个函数或一个类声明成 smolagents 的工具&…...

前端面试真题 2025最新版
文章目录 写在前文CSS怪异盒模型JS闭包闭包的形成闭包注意点 CSS选择器及优先级优先级 说说flex布局及相关属性Flex 容器相关属性:Flex 项目相关属性 响应式布局如何实现是否用过tailwindcss,有哪些好处好处缺点 说说对象的 prototype属性及原型说说 pro…...
面试八股文--数据库基础知识总结(1)
1、数据库的定义 数据库(DataBase,DB)简单来说就是数据的集合数据库管理系统(Database Management System,DBMS)是一种操纵和管理数据库的大型软件,通常用于建立、使用和维护数据库。数据库系统…...

10. docker nginx官方镜像使用方法
本文介绍docker nginx官方镜像使用方法,因为第一次用,在加上对docker也不是很熟,中间踩了一些坑,为了避免下一次用又踩坑,因此记录如下,也希望能够帮到其它小伙伴。 官方镜像页面:https://hub.d…...

[Web 安全] PHP 反序列化漏洞 —— PHP 反序列化漏洞演示案例
关注这个专栏的其他相关笔记:[Web 安全] 反序列化漏洞 - 学习笔记-CSDN博客 PHP 反序列化漏洞产生原因 PHP 反序列化漏洞产生的原因就是因为在反序列化过程中,unserialize() 接收的值可控。 0x01:环境搭建 这里笔者是使用 PhpStudy 搭建的环…...

es-head(es库-谷歌浏览器插件)
1.下载es-head插件压缩包,并解压缩 2.谷歌浏览器添加插件 3.使用...

第二十:【路由的props配置】
作用:让路由组件更方便的收到参数(可以将路由参数作为props传给组件) {name:xiang,path:detail/:id/:title/:content,component:Detail, 第一种方法:// props的对象写法,作用:把对象中的每一组key-valu…...

Vue 2全屏滚动动画实战:结合fullpage-vue与animate.css打造炫酷H5页面
引言 在移动端H5开发中,全屏滚动效果因其沉浸式体验而广受欢迎。如何快速实现带有动态加载动画的全屏滚动页面?本文将手把手教你使用 Vue 2、全屏滚动插件 fullpage-vue 和动画库 animate.css 3.5.1,打造一个高效且视觉冲击力强的H5页面。通…...

AF3 DataPipeline类process_pdb 方法解读
DataPipeline 类中的 process_pdb 方法用于从 PDB 文件中生成特定蛋白质链的特征,作为 AlphaFold3 预测的输入。它的流程与 process_mmcif 类似,但输入来源是 PDB 文件而非 MmcifObject。 源代码: def process_pdb(self,pdb_path: str,alignment_dir: str,is_distillation:…...

抓包工具 wireshark
1.什么是抓包工具 抓包工具是什么?-CSDN博客 2.wireshark的安装 【抓包工具】win 10 / win 11:WireShark 下载、安装、使用_windows抓包工具-CSDN博客 3.wireshark的基础操作 Wireshark零基础使用教程(超详细) - 元宇宙-Meta…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

Vite中定义@软链接
在webpack中可以直接通过符号表示src路径,但是vite中默认不可以。 如何实现: vite中提供了resolve.alias:通过别名在指向一个具体的路径 在vite.config.js中 import { join } from pathexport default defineConfig({plugins: [vue()],//…...
