【数据结构第十六节】实现链式结构二叉树(详细递归图解—呕心沥血版!)
必须有为成功付出代价的决心,然后想办法付出这个代价。云边有个稻草人-CSDN博客
这节课挺抽象(苦笑),没事,我会帮你!干就完了!
(目录在路上)
正文开始——
引言
用链表来表示一棵二叉树,即用链来指示元素的逻辑关系。通常的方法是链表中每个结点有三个域组成,数据域和左右指针域,左右指针分别用来给出该结点左孩子和右孩子所在链结点的存储地址,结构见下:
//创建链式结构二叉树的结构->二叉链
typedef int BTDataType;
typedef struct BinaryTreeNode
{BTDataType* data;struct BinaryTreeNode* left;//指定当前结点的左孩子struct BinaryTreeNode* right;//指定当前结点的右孩子
}BTNode;二叉树的创建方式比较复杂,为了更好地步入到二叉树内容中,我们先手动创建一棵链式二叉树。
//申请结点
BTNode* BuyNode(BTDataType x)
{BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));if (newnode == NULL){perror("malloc faile!");exit(1);}newnode->data = x;newnode->left = newnode->right = NULL;return newnode;
}BTNode* CreateTree()
{BTNode* node1 = BuyNode(1);BTNode* node2 = BuyNode(2);BTNode* node3 = BuyNode(3);BTNode* node4 = BuyNode(4);//改变指针指向,使其成为一棵链式二叉树node1->left = node2;node1->right = node3;node2->left = node4;return node1;}回顾二叉树的概念,二叉树分为空树和非空二叉树,非空二叉树由根节点、根节点的左子树和根节点的右子树组成的。

根节点的左子树和右子树分别又是由子树节点、子树结点的左子树和子树结点的右子树组成的,因此二叉树是递归式的,后序链式二叉树的操作基本都是按照概念实现的。
一、前中后序遍历
1.1 遍历规则
按照规则,二叉树的遍历有:前序 /中序/ 后序的遍历结构:
- 前序遍历(Preorder Traversal 亦称先序遍历):访问根结点的操作发生在遍历其左右子树之前,访问的顺序:根节点、左子树、右子树
- 中序遍历(Inorder Traversal):访问根节点的操作发生在遍历其左右子树之间,访问顺序:左子树、根节点、右子树
- 后序遍历(Postorder Traversal):访问根节点的操作发生在遍历其左右子树之后,访问顺序:左子树、右子树、根节点

1.2 代码实现
(1)前序遍历
//前序遍历
void PreOrder(BTNode* root)
{if (root == NULL){return;}printf("%d ", root->data);PreOrder(root->left);PreOrder(root->right);
}
该图里面,前序遍历结果为:1 2 4 3
(2)中序遍历
//中序遍历--左根右
void InOrder(BTNode* root)
{if (root == NULL){return;}InOrder(root->left);printf("%d ", root->data);InOrder(root->right);
} 中序遍历结果为:4 2 1 3

(3)后序遍历
//后序遍历--左右根
void PosOrder(BTNode* root)
{if (root == NULL){return;}PosOrder(root->left);PosOrder(root->right);printf("%d ", root->data);
}
二、结点个数以及高度等
2.1 二叉树结点个数

//求二叉树节点的个数
int BinaryTreeSize(BTNode* root)
{if (root == NULL){return 0;}return 1 + BinaryTreeSize(root->left) + BinaryTreeSize(root->right);
}2.2 二叉树叶子结点的个数

//二叉树叶子结点个数
int BinaryTreeLeafSize(BTNode* root)
{if (root == NULL){return 0;}if (root->left == NULL && root->right == NULL){return 1;}return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}
2.3 二叉树第K层结点的个数

//第K层节点个数
int BinaryTreeLevelKSize(BTNode* root,int k)
{if (root == NULL){return 0;}if (k == 1){return 1;}return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}2.4 求二叉树的高度/深度

//求二叉树高度/深度
int BinaryTreeDepth(BTNode* root)
{if (root == NULL){return 0;}int leftDep = BinaryTreeDepth(root->left);int rightDep = BinaryTreeDepth(root->right);return leftDep > rightDep ? leftDep + 1 : rightDep + 1;
}2.5 二叉树查找值为x的节点

//二叉树找值为x的结点
BTNode* BinaryFind(BTNode* root, BTDataType x)
{if (root == NULL){return NULL;}if (root->data == x){return root;}BTNode* leftFind = BinaryFind(root->left, x);if (leftFind){return leftFind;}BTNode* rightFind = BinaryFind(root->right, x);if (rightFind){return rightFind;}return NULL;
}2.6 二叉树的销毁

//二叉树的销毁
void BinaryTreeDestroy(BTNode** root)
{if (*root == NULL){return;}BinaryTreeDestroy(&((*root)->left));//注意这里的传参,传的是地址BinaryTreeDestroy(&((*root)->right));free(*root);*root = NULL;
}三、层序遍历

我们要提前实现一个队列的结构,(1)在下面的函数里面我们创建一个队列,并且别忘记队列的初始化和销毁,(2)同时要注意,我们前面学习的队列里面的数据是整型类型,这次我们要将结点插入到队列里面,所以我们要将队列里面的数据类型改为二叉树节点的类型,并且我们不能直接写二叉树节点的缩写那样,我们要写成 struct BinaryTreeNode* / struct BTNode* ,反正都不能少 struct,不然会报错。(3)还有一点,在我们的层序遍历代码里面当while循环结束的时候队列为NULL,下一步再进行队列的销毁的时候就会报错,因为我们前面实现的队列的销毁里面队列为空时不能销毁,所以assert会报错,所以我们可以把队列的销毁里面判断队列是否为空的那一步给注释掉。
提及到的代码需要注意的点都在下面,多看看!
//创建节点的结构
typedef struct BinaryTreeNode* QUDatatype;//这里需要注意
typedef struct QueueNode
{QUDatatype data;struct QueueNode* next;
}QueueNode;//销毁
void QueueDestroy(Queue* pq)
{assert(pq);//assert(!QueueEmpty(pq));//往这看,注释掉这里也没事,就算队列为空也没关系//此时pcur为NULL,进不去循环QueueNode* pcur = pq->phead;while (pcur){QueueNode* next = pcur->next;free(pcur);pcur = next;}pq->phead = pq->ptail = NULL;pq->size = 0;
}
//层序遍历
void LevelBinaryTree(BTNode* root)
{//先创建一个队列Queue q;QueueInit(&q);//取根节点入队列QueuePush(&q, root);while (!QueueEmpty(&q)){//打印队头数据BTNode* Front = QueueFront(&q);printf("%d ", Front->data);QueuePop(&Front);if (Front->left){QueuePush(&q, Front->left);}if (Front->right){QueuePush(&q, Front->right);}}QueueDestroy(&q);
}四、判断是否是完全二叉树
//判断是否是完全二叉树
bool BinaryTreeComplete(BTNode* root)
{Queue q;QueueInit(&q);QueuePush(&q,root);while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);//保证下次是最新的队头if (front == NULL){break;}QueuePush(&q, front->left);QueuePush(&q, front->right);}//队列不一定为空while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);if (front != NULL){QueueDestroy(&q);return false;}}QueueDestroy(&q);return true;
}
【图解】

五、本节课代码汇总
Queue.h
#pragma once
#include<stdbool.h>
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>//创建节点的结构
typedef struct BinaryTreeNode* QUDatatype;
typedef struct QueueNode
{QUDatatype data;struct QueueNode* next;
}QueueNode;//创建队列的结构
typedef struct Queue
{QueueNode* phead;QueueNode* ptail;int size;
}Queue;//初始化
void QueueInit(Queue* pq);//入队列
void QueuePush(Queue* pq,QUDatatype x);//判空
bool QueueEmpty(Queue* pq);//出队列
void QueuePop(Queue* pq);//取队头数据
QUDatatype QueueTop(Queue* pq);//去队尾数据
QUDatatype QueueBack(Queue* pq);//去队列中有效数据的个数
int QueueSize(Queue* pq);//销毁
void QueueDestroy(Queue* pq);Queue.c
#include"Queue.h"void QueueInit(Queue* pq)
{assert(pq);pq->phead = pq->ptail = NULL;pq->size = 0;
}//入队列
void QueuePush(Queue* pq, QUDatatype x)
{assert(pq);//现申请新的结点QueueNode* newnode = (QueueNode*)malloc(sizeof(QueueNode));if (newnode == NULL){perror("malloc fail!");exit(1);}newnode->data = x;newnode->next = NULL;//如果为空if (pq->phead == NULL){pq->phead = pq->ptail = newnode;}else{pq->ptail->next = newnode;pq->ptail = newnode;}pq->size++;
}//判空
bool QueueEmpty(Queue* pq)
{assert(pq);return pq->phead == NULL;
}//出队列
void QueuePop(Queue* pq)
{assert(pq);assert(!QueueEmpty(pq));if (pq->phead == pq->ptail){free(pq->phead);pq->phead = pq->ptail = NULL;}else{QueueNode* pcur = pq->phead->next;free(pq->phead);pq->phead = pcur;}pq->size--;
}//取队头数据
QUDatatype QueueTop(Queue* pq)
{assert(pq);assert(!QueueEmpty(pq));return pq->phead->data;}//去队尾数据
QUDatatype QueueBack(Queue* pq)
{assert(pq);assert(!QueueEmpty(pq));return pq->ptail->data;
}int QueueSize(Queue* pq)
{assert(pq);/*QueueNode* pcur = pq->phead;int count = 0;while (pcur){count++;QueuePop(pq);pcur = pq->phead;}*//*return count;*/return pq->size;
}//销毁
void QueueDestroy(Queue* pq)
{assert(pq);//assert(!QueueEmpty(pq));QueueNode* pcur = pq->phead;while (pcur){QueueNode* next = pcur->next;free(pcur);pcur = next;}pq->phead = pq->ptail = NULL;pq->size = 0;
}Tree.h
#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>//创建链式结构二叉树的结构->二叉链
typedef int BTDataType;
typedef struct BinaryTreeNode
{BTDataType data;struct BinaryTreeNode* left;//指定当前节点的左孩子struct BinaryTreeNode* right;//指定当前节点的右孩子
}BTNode;//申请节点
BTNode* BuyNode(BTDataType x);//前序遍历
void PreOrder(BTNode* root);//中序遍历
void InOrder(BTNode* root);//后序遍历
void PosOrder(BTNode* root);//求二叉树节点的个数
int BinaryTreeSize(BTNode* root);//二叉树叶子结点个数
int BinaryTreeLeafSize(BTNode* root);//第K层节点个数
int BinaryTreeLevelKSize(BTNode* root,int k);//求二叉树高度/深度
int BinaryTreeDepth(BTNode* root);//找X的结点
BTNode* BinaryFind(BTNode* root, BTDataType x);//二叉树的销毁
void BinaryTreeDestroy(BTNode** root);//层序遍历
void LevelBinaryTree(BTNode* root);//判断是否是完全二叉树
bool BinaryTreeComplete(BTNode* root);Tree.c
#include"Tree.h"
#include"Queue.h"//申请节点
BTNode* BuyNode(BTDataType x)
{BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));if (newnode == NULL){perror("malloc faile!");exit(1);}newnode->data = x;newnode->left = newnode->right = NULL;return newnode;
}//前序遍历-
void PreOrder(BTNode* root)
{if (root == NULL){return;}printf("%d ", root->data);PreOrder(root->left);PreOrder(root->right);
}//中序遍历--左根右
void InOrder(BTNode* root)
{if (root == NULL){return;}InOrder(root->left);printf("%d ", root->data);InOrder(root->right);
} //后序遍历--左右根
void PosOrder(BTNode* root)
{if (root == NULL){return;}PosOrder(root->left);PosOrder(root->right);printf("%d ", root->data);
}//求二叉树节点的个数
int BinaryTreeSize(BTNode* root)
{if (root == NULL){return 0;}return 1 + BinaryTreeSize(root->left) + BinaryTreeSize(root->right);
}//二叉树叶子结点个数
int BinaryTreeLeafSize(BTNode* root)
{if (root == NULL){return 0;}if (root->left == NULL && root->right == NULL){return 1;}return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}//第K层节点个数
int BinaryTreeLevelKSize(BTNode* root,int k)
{if (root == NULL){return 0;}if (k == 1){return 1;}return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}//求二叉树高度/深度
int BinaryTreeDepth(BTNode* root)
{if (root == NULL){return 0;}int leftDep = BinaryTreeDepth(root->left);int rightDep = BinaryTreeDepth(root->right);return leftDep > rightDep ? leftDep + 1 : rightDep + 1;
}//二叉树找值为x的结点
BTNode* BinaryFind(BTNode* root, BTDataType x)
{if (root == NULL){return NULL;}if (root->data == x){return root;}BTNode* leftFind = BinaryFind(root->left, x);if (leftFind){return leftFind;}BTNode* rightFind = BinaryFind(root->right, x);if (rightFind){return rightFind;}return NULL;
}//二叉树的销毁
void BinaryTreeDestroy(BTNode** root)
{if (*root == NULL){return;}BinaryTreeDestroy(&((*root)->left));BinaryTreeDestroy(&((*root)->right));free(*root);*root = NULL;
}//层序遍历
void LevelBinaryTree(BTNode* root)
{//先创建一个队列Queue q;QueueInit(&q);//取根节点入队列QueuePush(&q, root);while (!QueueEmpty(&q)){//打印队头数据BTNode* Front = QueueFront(&q);printf("%d ", Front->data);QueuePop(&Front);if (Front->left){QueuePush(&q, Front->left);}if (Front->right){QueuePush(&q, Front->right);}}QueueDestroy(&q);
}//判断是否是完全二叉树
bool BinaryTreeComplete(BTNode* root)
{Queue q;QueueInit(&q);QueuePush(&q,root);while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);if (front == NULL){break;}QueuePush(&q, front->left);QueuePush(&q, front->right);}//队列不为空while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);if (front != NULL){QueueDestroy(&q);return false;}}QueueDestroy(&q);return true;
}test.c
#include"Tree.h"BTNode* CreateTree()
{BTNode* node1 = BuyNode(1);BTNode* node2 = BuyNode(2);BTNode* node3 = BuyNode(3);BTNode* node4 = BuyNode(4);node1->left = node2;node1->right = node3;node2->left = node4;return node1;}int main()
{BTNode* node = CreateTree();/*PreOrder(node);printf("\n");InOrder(node);printf("\n");PosOrder(node);*/printf("NodeSize:%d\n", BinaryTreeSize(node));printf("NodeSize:%d\n", BinaryTreeSize(node));printf("NodeSize:%d\n", BinaryTreeSize(node));printf("LeafSize:%d\n", BinaryTreeLeafSize(node));printf("%d\n", BinaryTreeLevelKSize(node, 3));printf("%d\n", BinaryTreeDepth(node));BTNode* find = BinaryFind(node, 22);printf("%s\n", find == NULL ? "没找到\n" : "找到了!\n");LevelBinaryTree(node);bool ret = BinaryTreeComplete(node);printf("%s\n", ret == false ? "不是完全二叉树\n" : "是完全二叉树\n");BinaryTreeDestroy(&node);return 0;
}我感觉这节递归还是挺难理解的,感觉函数递归进行的过程不好想象,层层递归就比较难以理解透彻,我会忘记自己递归到那个地方了绕不回去了就很烧脑筋,难想的时候呢我就得画出函数进行栈帧的创建与销毁,这样一步一步来还是比较好的。对了,我画的红箭头还有绿箭头可以看成是函数栈帧的创建与销毁。把详细的函数的栈帧的创建与销毁多想几遍函数的递归应该就会好想象一点了。这节课我啃了两天了,后续还得多回顾理解多敲代码,告诉自己,别畏难,很难,但也得一步一步走下去,总不能放弃吧,那就坚定不移的前进!(这节课的博客真难写呀啊啊啊——)
知识点有不对的地方还请多多指教(抱拳)
完——
终——Relaxing Time!
好好休息一下,继续战斗!昨天又发现了一首好听的歌(^-^)V)分享给你
————————————《Falling U》————————————
Falling U_T-ara_高音质在线试听_Falling U歌词|歌曲下载_酷狗音乐

至此结束——
我是云边有个稻草人
期待与你的下一次相遇!
相关文章:

【数据结构第十六节】实现链式结构二叉树(详细递归图解—呕心沥血版!)
必须有为成功付出代价的决心,然后想办法付出这个代价。云边有个稻草人-CSDN博客 这节课挺抽象(苦笑),没事,我会帮你!干就完了! (目录在路上) 正文开始—— 引言 用链表…...
】从当下到未来:Python爬虫技术的进阶之路)
【Python爬虫(100)】从当下到未来:Python爬虫技术的进阶之路
【Python爬虫】专栏简介:本专栏是 Python 爬虫领域的集大成之作,共 100 章节。从 Python 基础语法、爬虫入门知识讲起,深入探讨反爬虫、多线程、分布式等进阶技术。以大量实例为支撑,覆盖网页、图片、音频等各类数据爬取,还涉及数据处理与分析。无论是新手小白还是进阶开发…...
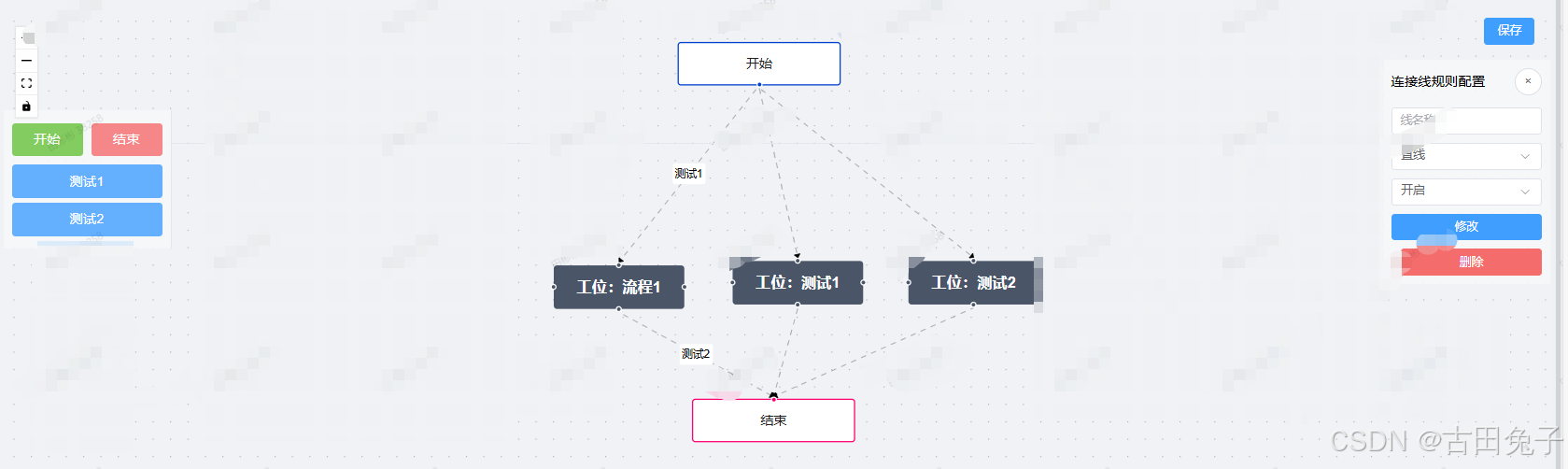
Vue-Flow绘制流程图(Vue3+ElementPlus+TS)简单案例
本文是vue3Elementplusts框架编写的简单可拖拽绘制案例。 1.效果图: 2.Index.vue主代码: <script lang"ts" setup> import { ref, markRaw } from "vue"; import {VueFlow,useVueFlow,MarkerType,type Node,type Edge } fro…...

CNN:卷积网络中设计1×1夹在主要卷积核如3×3前后的作用
话不多说直接上图举例: 像在 ResNet 的 Bottleneck 结构 中,1x1 卷积 被放置在 3x3 卷积 的前后,这种设计有以下几个关键作用和优势: 1. 降低计算复杂度 问题:直接使用 3x3 卷积计算量较大,尤其是当输入和…...

esp8266 rtos sdk开发环境搭建
1. 安装必要的工具 1.1 安装 Git Git 用于从远程仓库克隆代码,你可以从Git 官方网站下载 Windows 版本的安装程序。安装过程中可保持默认设置,安装完成后,在命令提示符(CMD)或 PowerShell 中输入git --version&#…...

【深度学习】矩阵的核心问题解析
一、基础问题 1. 如何实现两个矩阵的乘法? 问题描述:给定两个矩阵 A A A和 B B B,编写代码实现矩阵乘法。 解法: 使用三重循环实现标准矩阵乘法。 或者使用 NumPy 的 dot 方法进行高效计算。 def matrix_multiply(A, B):m, n …...

DeepSeek模型昇腾部署优秀实践
2024年12月26日,DeepSeek-V3横空出世,以其卓越性能备受瞩目。该模型发布即支持昇腾,用户可在昇腾硬件和MindIE推理引擎上实现高效推理,但在实际操作中,部署流程与常见问题困扰着不少开发者。本文将为你详细阐述昇腾 De…...

从 Spring Boot 2 升级到 Spring Boot 3 的终极指南
一、升级前的核心准备 1. JDK 版本升级 Spring Boot 3 强制要求 Java 17 及以上版本。若当前项目使用 Java 8 或 11,需按以下步骤操作: 安装 JDK 17:从 Oracle 或 OpenJDK 官网下载,配置环境变量(如 JAVA_HOME&…...

mysql架构查询执行流程(图解+描述)
目录 mysql架构查询执行流程 图解 描述 mysql架构查询执行流程 图解 描述 用户连接到数据库后,由连接器处理 连接器负责跟客户端建立连接、获取权限、维持和管理连接 客户端发送一条查询给服务器 服务器先检查查询缓存,如果命中缓存,则立…...

20分钟 Bash 上手指南
文章目录 bash 概念与学习目的第一个 bash 脚本bash 语法变量的使用位置参数管道符号(过滤条件)重定向符号条件测试命令条件语句case 条件分支Arrayfor 循环函数exit 关键字 bash 脚本记录历史命令查询文件分发内容 bash 概念与学习目的 bash࿰…...

事故02分析报告:慢查询+逻辑耦合导致订单无法生成
一、事故背景与现象 时间范围 2022年2月3日 18:11~18:43(历时32分钟) 受影响系统 系统名称角色影响范围dc3订单数据库主库订单生成、事务回滚dc4订单数据库从库数据同步、容灾切换 业务影响 核心业务:手机点餐、C扫B支付订单无法推送至…...

vant2 vue2 两个输入框联动验证遇到的问题
需求是两个输入框,一个输上限A,一个输下限B <van-fieldv-model"formData.upperLimit"name"upperLimit"type"number"label"上限"required:formatter"formatter"/><van-fieldv-model"for…...

硬件工程师入门教程
1.欧姆定律 测电压并联使用万用表测电流串联使用万用表,红入黑出 2.电阻的阻值识别 直插电阻 贴片电阻 3.电阻的功率 4.电阻的限流作用 限流电阻阻值的计算 单位换算关系 5.电阻的分流功能 6.电阻的分压功能 7.电容 电容简单来说是两块不连通的导体加上中间的绝…...

如何使用Docker搭建哪吒监控面板程序
哪吒监控(Nezha Monitoring)是一款自托管、轻量级的服务器和网站监控及运维工具,旨在为用户提供实时性能监控、故障告警及自动化运维能力。 文档地址:https://nezha.wiki/ 本章教程,使用Docker方式安装哪吒监控面板,在此之前,你需要提前安装好Docker. 我当前使用的操作系…...

python-leetcode 45.二叉树转换为链表
题目: 给定二叉树的根节点root,请将它展开为一个单链表: 展开后的单链表应该使用同样的TreeNode,其中right子指针指向链表中的下一个节点,而左子指针始终为空 展开后的单链表应该与二叉树先序遍历顺序相同 方法一:二叉树的前序…...

uni小程序wx.switchTab有时候跳转错误tab问题,解决办法
在一个子页面里面使用uni.switchTab或者wx.switchTab跳转到tab菜单的时候,先发送了一个请求,然后执行跳转到tab菜单,但是这个时候,出错了........也是非常的奇怪,不加请求就没问题......但是业务逻辑就是要先执行某个请…...

【一起学Rust | 框架篇 | Tauri2.0框架】在Tauri应用中设置Http头(Headers)
文章目录 前言一、配置准备1. 检查版本2. 使用条件3. 支持的请求头(并不是全部支持) 二、使用步骤1. 如何配置header2. 框架集成1. 对于Vite系列、Nuxt、Next.js这种前端框架Vite系列框架Angular系列框架Nuxt系列框架Next.js系列框架 2. 对于Yew和Leptos…...

STM32G473VET6 在 Keil MDK 下手动移植 FreeRTOS 指南
下面将详细介绍如何在 Keil MDK 环境下将 FreeRTOS 手动移植到 STM32G473VET6 微控制器上。内容涵盖工程创建、获取源码、文件组织、移植层适配、测试任务编写以及编译调试等步骤。 1. 工程搭建(Keil 项目创建) 创建基础工程:首先准备一个基…...
波导阵列天线 学习笔记11双极化全金属垂直公共馈电平板波导槽阵列天线
摘要: 本communicaition提出了一种双极化全金属垂直公共馈电平板波导槽阵列天线。最初提出了一种公共馈电的单层槽平板波导来实现双极化阵列。此设计消除了传统背腔公共馈电的复杂腔体边缘的必要性,提供了一种更简单的天线结构。在2x2子阵列种发展了宽十…...

DeepSeek-R1自写CUDA内核跑分屠榜:开启GPU编程自动化新时代
引言 在AI领域,深度学习模型的性能优化一直是研究者们关注的核心。最近,斯坦福和普林斯顿的研究团队发现,DeepSeek-R1生成的自定义CUDA内核不仅超越了OpenAI的o1和Claude 3.5 Sonnet,还在KernelBench框架中取得了总排名第一的好成…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

Kubernetes 网络模型深度解析:Pod IP 与 Service 的负载均衡机制,Service到底是什么?
Pod IP 的本质与特性 Pod IP 的定位 纯端点地址:Pod IP 是分配给 Pod 网络命名空间的真实 IP 地址(如 10.244.1.2)无特殊名称:在 Kubernetes 中,它通常被称为 “Pod IP” 或 “容器 IP”生命周期:与 Pod …...

【Elasticsearch】Elasticsearch 在大数据生态圈的地位 实践经验
Elasticsearch 在大数据生态圈的地位 & 实践经验 1.Elasticsearch 的优势1.1 Elasticsearch 解决的核心问题1.1.1 传统方案的短板1.1.2 Elasticsearch 的解决方案 1.2 与大数据组件的对比优势1.3 关键优势技术支撑1.4 Elasticsearch 的竞品1.4.1 全文搜索领域1.4.2 日志分析…...

