CAN总线通信协议学习1——物理层

首先来看看CAN是怎么产生的：简单理解，CAN就是一种“拥有特别连接方式”的数据传输的总线，其有特定的一些规则。

（注：资料及图片来源于知乎博主TOMOCAT。）

CAN总线的结构

查阅参考文献，OSI标准主要将CAN总线分为物理层、数据链路层、应用层（有客户自己设定），（下图中的表示层、传输层等等在我看来就是在数据处理中设计到的范畴，主要部分还是上述三层），而应用层由客户自己设定，那么有标准的就只能是物理层和数据链层，以下主要讲解这两个部分。

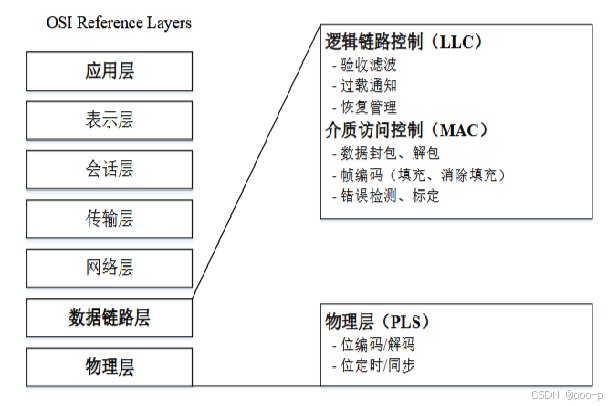
CAN的物理层

CAN总线分为高速CAN和低速CAN，顾名思义，

• 高速CAN传输速度快但距离短
• 低速CAN传输速度慢但距离远。

• 高速CAN闭环
• 低俗CAN开环

在此我们主要学习高速CAN。

高速CAN的拓扑结构（硬件电路）

首先，CAN总线是将信号转换为差分信号进行传输。

高速CAN的硬件电路图如上所示，可以看到：

---

      设备即传输数据的电子控制单元，其将数据通过TX和RX线传输给CAN收发器

  CAN收发器通过电平转换、输出驱动、输入采样等操作将收到的数据传到CAN_H和CAN_L

  CAN_H和CAN_L将传输数据转为差分信号进行传输

---

其次，CAN总线其实就是CAN_H和CAN_L组成两根闭环线，且CAN_H和CAN_L两端添加120Ω的终端电阻，终端电阻的作用：

（1）防止回波反射（不太懂）

（2）当无设备工作时，使高速CAN默认为收紧状态，两线电压差为0。与后续CAN总线电平的设置相关（也不太懂哔哩哔哩上说的收紧拉开）

CAN电平标准

看高速CAN，CAN_H和CAN_L所谓“收紧”时，即电压差为0V（或-0.5V到0.05V），表示1；CAN_H和CAN_L所谓“拉开”时，即电压差为2V（或1.5V~3V，有一个误差范围，看设定），表示0。（低速CAN则类似这样看）。

• 这里要注意，逻辑1被定义为隐形，逻辑0被定义为显性，这与我们的使用习惯不太相同。
• 当显性和隐性电平同时出现，表示为显性电平，即0和1同时出现，表示0（0强于1）。

CAN收发器（不太懂，留个图，后面来补上）

注：本文将开始进行CAN总线通信协议得学习，以上均是通过学习参考文献、哔哩哔哩网站上江协科技官方号以及网络资源所得的个人经验，如有侵权，请联系我，欢迎指正。