Lumerical INTERCONNECT 中的自相位调制 (SPM)

一、自相位调制的数学介绍

A.非线性薛定谔方程（NLSE）：

NLSE 是光学中的一个关键方程。它告诉我们光脉冲在具有非线性和色散特性的介质中的行为方式。该方程如下所示：

i ∂A/∂z + β2/2 ∂²A/∂t² + γ|A|²A = 0
其中：
- A 表示光场的复包络。
- β2 表示群速度色散参数。
- γ 为非线性系数。
- z 表示传播距离。
- t 代表延迟时间帧。

NLSE 中的术语 (γ|A|²A) 是 SPM 效应的象征。它传达了一个基本概念：脉冲相位的调制与其强度梯度有着内在联系。

自相位调制的底层物理原理

A.克尔效应：

SPM 的核心是克尔效应。该效应描述了介质的折射率如何根据穿过它的光的强度进行动态调整。折射率的这种变化引起的相移可以量化为：
Δϕ = γP₀L
在此等式中：
- P₀ 表示脉冲的峰值功率。-
L 表示介质的长度。

B. 光谱增宽：

光穿过介质时会发生的一种现象称为光谱增宽。即脉冲的频谱变宽。这种增宽可以看作频谱中的边带。这是由于脉冲强度而在波导内部发生的相互作用的明显迹象。

III. 使用 Lumerical INTERCONNECT 进行 SPM 模拟

Lumerical 的 INTERCONNECT 软件是一款功能强大的光学电路模拟工具。它特别适合观察 SPM 等非线性效应。您可以在该软件中使用的一个功能是 NLSE 波导 (NLSE-WGD) 元件。它旨在模拟波导在存在非线性效应时的行为。

在 INTERCONNECT 中设置电路时，您可以通过不同的方式看到 SPM 的效果。例如，在频域中，您可以看到脉冲的频谱随着功率的增加而变宽。这就是我们之前讨论过的频谱展宽。但在时域中，即使您改变功率，脉冲的形状也不会真正改变。这告诉我们一些有关波导中属性平衡的信息。

图 1 为我们展示了 INTERCONNECT 内部的光路。它就像一张地图，显示了光源、监视器和波导等不同部分是如何连接的。通过查看此图，我们可以了解光信号的旅程以及我们可以测量或更改事物的位置。

 

图 1：INTERCONNECT 中的电路设置方式

图 2 是关于细节的。它显示了如何在波导元件中设置不同的参数。例如色散、克尔效应、波导长度，甚至损耗量。能够控制这些设置意味着我们可以进行接近真实情况的模拟。

 

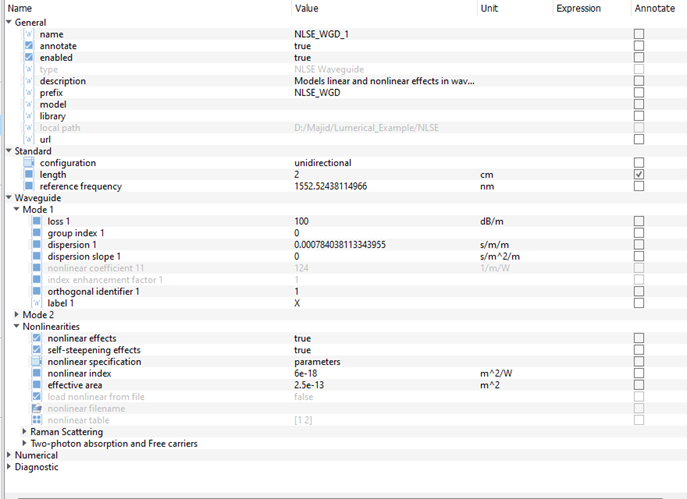
图 2：在波导中设置参数

图 3 让我们看到使用不同功率水平时的 SPM 效应，但仅限于频域。它就像脉冲频谱的快照。当我们改变功率时，频谱也会发生变化。我们可以看到它变宽了，这就是频谱展宽的作用。这是波导内部非线性相互作用的直接结果。

 

图 3：不同功率水平下的 SPM 效应