DeepSeek本地接口调用(Ollama)
前言
上篇博文,我们通过Ollama搭建了本地的DeepSeek模型,本文主要是方便开发人员,如何通过代码或工具,通过API接口调用本地deepSeek模型
前文:DeepSeek-R1本地搭建_deepseek 本地部署-CSDN博客
注:本文不仅仅适用DeepSeek, 通过Ollama安装的模型,都适用
一:Ollama接口
上文中,我们采用ollama来搭建deepSeek r1模型,所有调用本地deepSeek模型,可以使用ollama开放的API来操作。
ollama默认开放端口:11434
ollama接口文档地址:https://github.com/ollama/ollama/blob/main/docs/api.md
里面包含各种接口,包括如下:(访问文档,点击自行选择)
注意:文档是英文,看不懂用浏览器翻一下

二:调用案例(创建聊天)
API文档地址:(参考)https://github.com/ollama/ollama/blob/main/docs/api.md#generate-a-chat-completion![]() https://github.com/ollama/ollama/blob/main/docs/api.md#generate-a-chat-completion
https://github.com/ollama/ollama/blob/main/docs/api.md#generate-a-chat-completion
接口地址:http://localhost:11434/api/chat
请求方式:POST
请求类型:JSON
请求内容:
{"model": "deepseek-r1:1.5b","messages": [{"role": "user","content": "你好?"}]
}注:这里model代码你的模型,content是你要聊天的内容,role指代角色,还要其他参数,请参考官方文档。
POSTMAN访问如下:

三:调用案例(生成请求)
API文档地址:(参考)https://github.com/ollama/ollama/blob/main/docs/api.md#generate-a-completion![]() https://github.com/ollama/ollama/blob/main/docs/api.md#generate-a-completion
https://github.com/ollama/ollama/blob/main/docs/api.md#generate-a-completion
接口地址:http://localhost:11434/api/generate
请求方式:POST
请求类型:JSON
请求内容:
{"model": "deepseek-r1:1.5b","prompt": "你好","stream": false
}注:如果stream设置为false,响应将是单个 JSON 对象
返回结果:
{"model": "deepseek-r1:1.5b","created_at": "2025-03-04T08:40:06.4879238Z","response": "<think>\n\n</think>\n\n你好!很高兴见到你,有什么我可以帮忙的吗?","done": true,"done_reason": "stop","total_duration": 951604700,"load_duration": 23765300,"prompt_eval_count": 4,"prompt_eval_duration": 57000000,"eval_count": 17,"eval_duration": 870000000
}POSTMAN:

四:其他API
请参考官方文档:
https://github.com/ollama/ollama/blob/main/docs/api.md

相关文章:

DeepSeek本地接口调用(Ollama)
前言 上篇博文,我们通过Ollama搭建了本地的DeepSeek模型,本文主要是方便开发人员,如何通过代码或工具,通过API接口调用本地deepSeek模型 前文:DeepSeek-R1本地搭建_deepseek 本地部署-CSDN博客 注:本文不仅…...

自由学习记录(41)
代理服务器的核心功能是在客户端(用户设备)和目标服务器(网站/资源服务器)之间充当“中介”,具体过程如下: 代理服务器的工作流程 当客户端希望访问某个网站(比如 example.com)时&…...

【编写UI自动化测试集】Appium+Python+Unittest+HTMLRunner
简介 获取AppPackage和AppActivity 定位UI控件的工具 脚本结构 PageObject分层管理 HTMLTestRunner生成测试报告 启动appium server服务 以python文件模式执行脚本生成测试报告 下载与安装 下载需要自动化测试的App并安装到手机 获取AppPackage和AppActivity 方法一 有源码的…...

大模型如何协助知识图谱进行实体关系之间的分析
大模型在知识图谱中协助进行实体关系分析的方式主要体现在以下几个方面: 增强数据标注与知识抽取 大模型通过强大的自然语言处理能力,能够高效地对原始数据进行实体、关系和事件的标注,从而提高数据处理的效率和准确性。例如,Deep…...

推荐几款优秀的PDF转电子画册的软件
当然可以!以下是几款优秀的PDF转电子画册的软件推荐,内容简洁易懂,这些软件都具有易用性和互动性,适合不同需求的用户使用。 ❶ FLBOOK|在线创作平台 支持PDF直接导入生成仿真翻页电子书。提供15主题模板与字体库&a…...

【大模型技术】LlamaFactory 的原理解析与应用
LlamaFactory 是一个基于 LLaMA 系列模型(如 LLaMA、LLaMA2、Vicuna 等)的开源框架,旨在帮助开发者和研究人员快速实现大语言模型(LLM, Large Language Model)的微调、推理和部署。它提供了一套完整的工具链࿰…...

Golang依赖注入实战:从容器管理到应用实践
#作者:曹付江 文章目录 1、示例: 管理依赖关系的容器1.1. 日志记录器设置1.2. 数据库连接设置1.3. 管理依赖关系的容器 2、如何使用容器3、结论 依赖注入(DI)是一种在软件应用程序中促进松散耦合和可测试性的设计模式。它允许将依…...

Node.js二:第一个Node.js应用
精心整理了最新的面试资料和简历模板,有需要的可以自行获取 点击前往百度网盘获取 点击前往夸克网盘获取 创建的时候我们需要用到VS code编写代码 我们先了解下 Node.js 应用是由哪几部分组成的: 1.引入 required 模块:我们可以使用 requi…...

【Python爬虫】利用代理IP爬取跨境电商AI选品分析
引言 随着DeepSeek的流行,越来越多的用户开始尝试将AI工具融入到日常工作当中,借助AI的强大功能提高工作效率。最近又掀起了一波企业出海的小高潮,那么如果是做跨境电商业务,怎么将AI融入工作流中呢?在做跨境电商的时候…...
)
生命周期总结(uni-app、vue2、vue3生命周期讲解)
一、vue2生命周期 Vue2 的生命周期钩子函数分为 4 个阶段:创建、挂载、更新、销毁。 1. 创建阶段 beforeCreate:实例初始化之后,数据观测和事件配置之前。 created:实例创建完成,数据观测和事件配置已完成,…...
)
计算机数据库三级刷题总结(博主89分已过,总结的内容分享)
计算机数据库三级刷题总结(博主89分已过,总结的内容分享) 文章目录 计算机数据库三级刷题总结(博主89分已过,总结的内容分享)一、 数据库设计阶段二、事务相关三、数据库设计顺序四、数据库三级模式与二层映…...

mfc140u.dll是什么?当程序遭遇mfc140u.dll问题:快速恢复正常的秘诀
在使用Windows操作系统运行某些软件时,不少用户会遇到令人头疼的mfc140u.dll文件丢失错误。mfc140u.dll这个错误一旦出现,往往导致相关程序无法正常启动或运行,给用户带来诸多不便。这天的这篇文章将给大家分析mfc140u.dll是什么?…...

AI是否能真正理解人类情感?从语音助手到情感机器人
引言:AI与情感的交集 在过去的几十年里,人工智能(AI)的发展速度令人惊叹,从简单的语音识别到如今的深度学习和情感计算,AI已经深入到我们生活的方方面面。尤其是在语音助手和情感机器人领域,AI不…...

3.3.2 Proteus第一个仿真图
文章目录 文章介绍0 效果图1 新建“点灯”项目2 添加元器件3 元器件布局接线4 补充 文章介绍 本文介绍:使用Proteus仿真软件画第一个仿真图 0 效果图 1 新建“点灯”项目 修改项目名称和路径,之后一直点“下一步”直到完成 2 添加元器件 点击元…...

JetBrains学生申请
目录 JetBrains学生免费授权申请 IDEA安装与使用 第一个JAVA代码 1.利用txt文件和cmd命令运行 2.使用IDEA新建项目 JetBrains学生免费授权申请 本教程采用学生校园邮箱申请,所以要先去自己的学校申请校园邮箱。 进入JetBrains官网 点击立即申请,然…...

深入探索WebGL:解锁网页3D图形的无限可能
深入探索WebGL:解锁网页3D图形的无限可能 引言 。WebGL,作为这一变革中的重要技术,正以其强大的功能和广泛的应用前景,吸引着越来越多的开发者和设计师的关注。本文将深入剖析WebGL的核心原理、关键技术、实践应用,并…...

SQL进阶技巧:上课时长计算
目录 0 问题描述 1 数据准备 2 问题解决 核心难点 时间区间标记与分组 区间合并与时长计算...

“沂路畅通”便利服务平台:赋能同城物流,构建高效畅通的货运生态
“沂路畅通”便利服务平台:赋能同城物流,构建高效畅通的货运生态 随着城市化进程的加速,同城物流需求迅速增长,然而货运过程中仍然存在信息不对称、资源浪费、司机服务体验差等痛点。临沂呆马区块链网络科技有限公司(…...

文件上传靶场(1--9关)
实验环境: 1,upload的靶场环境可以去GitHub上自行查找 2,打开小皮面板的nginx和数据库 3,将文件上传的靶场部署到本地: 放到小皮的phpstduy_pro的www下面 小提示: 另外如果你用的是php7的版本建议将版…...

嵌入式 ARM Linux 系统构成(1):Bootloader层
目录 一、Bootloader 概述 1.1 核心作用 1.2 典型启动流程 二、ARM Bootloader 架构详解 2.1 多阶段启动设计 2.2 关键代码流程 2.3. Bootloader的加载过程 2.4. Bootloader的加载方式 2.5. Bootloader 的移植 三、常见的Bootloader介绍 3.1. U-Boot 3.2. vivi …...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

命令行关闭Windows防火墙
命令行关闭Windows防火墙 引言一、防火墙:被低估的"智能安检员"二、优先尝试!90%问题无需关闭防火墙方案1:程序白名单(解决软件误拦截)方案2:开放特定端口(解决网游/开发端口不通)三、命令行极速关闭方案方法一:PowerShell(推荐Win10/11)方法二:CMD命令…...

内窥镜检查中基于提示的息肉分割|文献速递-深度学习医疗AI最新文献
Title 题目 Prompt-based polyp segmentation during endoscopy 内窥镜检查中基于提示的息肉分割 01 文献速递介绍 以下是对这段英文内容的中文翻译: ### 胃肠道癌症的发病率呈上升趋势,且有年轻化倾向(Bray等人,2018&#x…...
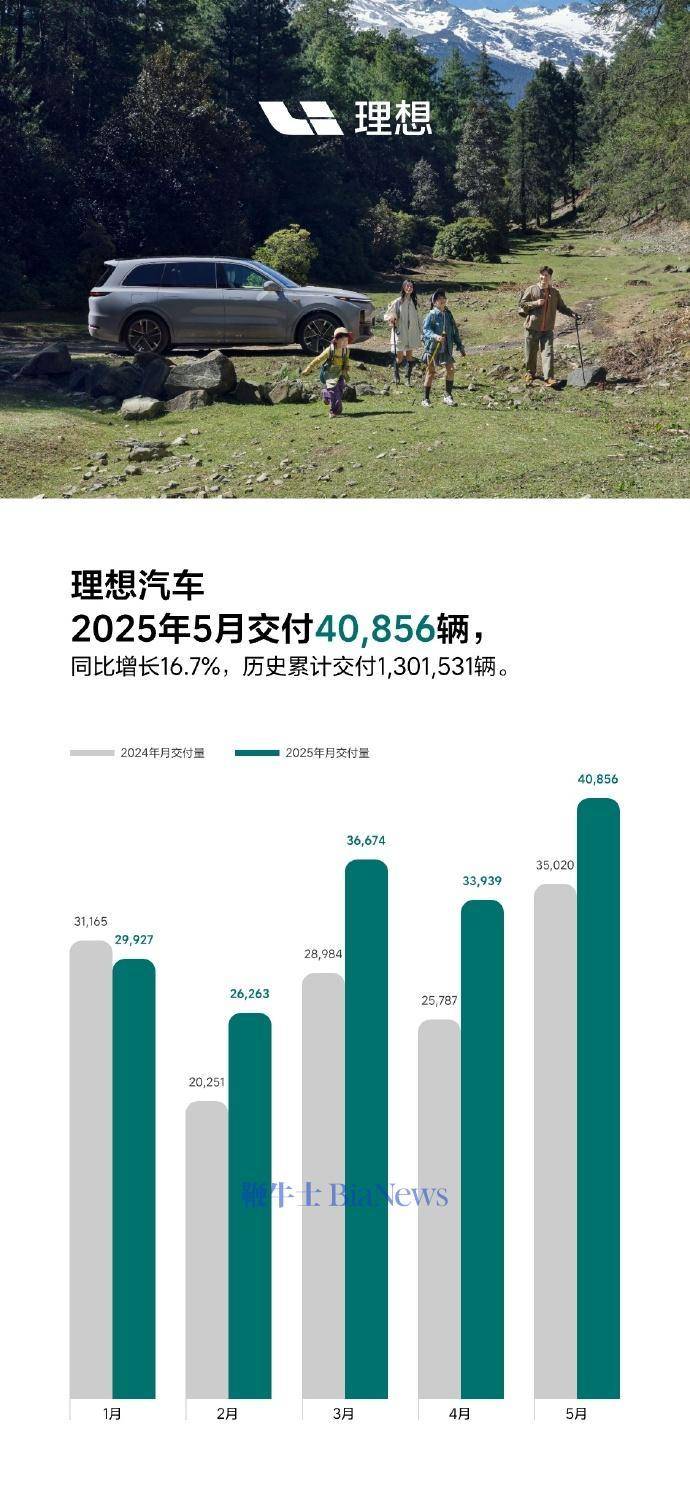
理想汽车5月交付40856辆,同比增长16.7%
6月1日,理想汽车官方宣布,5月交付新车40856辆,同比增长16.7%。截至2025年5月31日,理想汽车历史累计交付量为1301531辆。 官方表示,理想L系列智能焕新版在5月正式发布,全系产品力有显著的提升,每…...

Pandas 可视化集成:数据科学家的高效绘图指南
为什么选择 Pandas 进行数据可视化? 在数据科学和分析领域,可视化是理解数据、发现模式和传达见解的关键步骤。Python 生态系统提供了多种可视化工具,如 Matplotlib、Seaborn、Plotly 等,但 Pandas 内置的可视化功能因其与数据结…...

Centos 7 服务器部署多网站
一、准备工作 安装 Apache bash sudo yum install httpd -y sudo systemctl start httpd sudo systemctl enable httpd创建网站目录 假设部署 2 个网站,目录结构如下: bash sudo mkdir -p /var/www/site1/html sudo mkdir -p /var/www/site2/html添加测试…...

