直接法估计相机位姿
引入
在前面的文章:运动跟踪——Lucas-Kanade光流中,我们了解到特征点法存在一些缺陷,并且用光流法追踪像素点的运动来替代特征点法进行特征点匹配的过程来解决这些缺陷。而这篇文章要介绍的直接法则是通过计算特征点在下一时刻图像中的位置来进一步缩短算法计算时间。
直接法估计相机位姿的推导
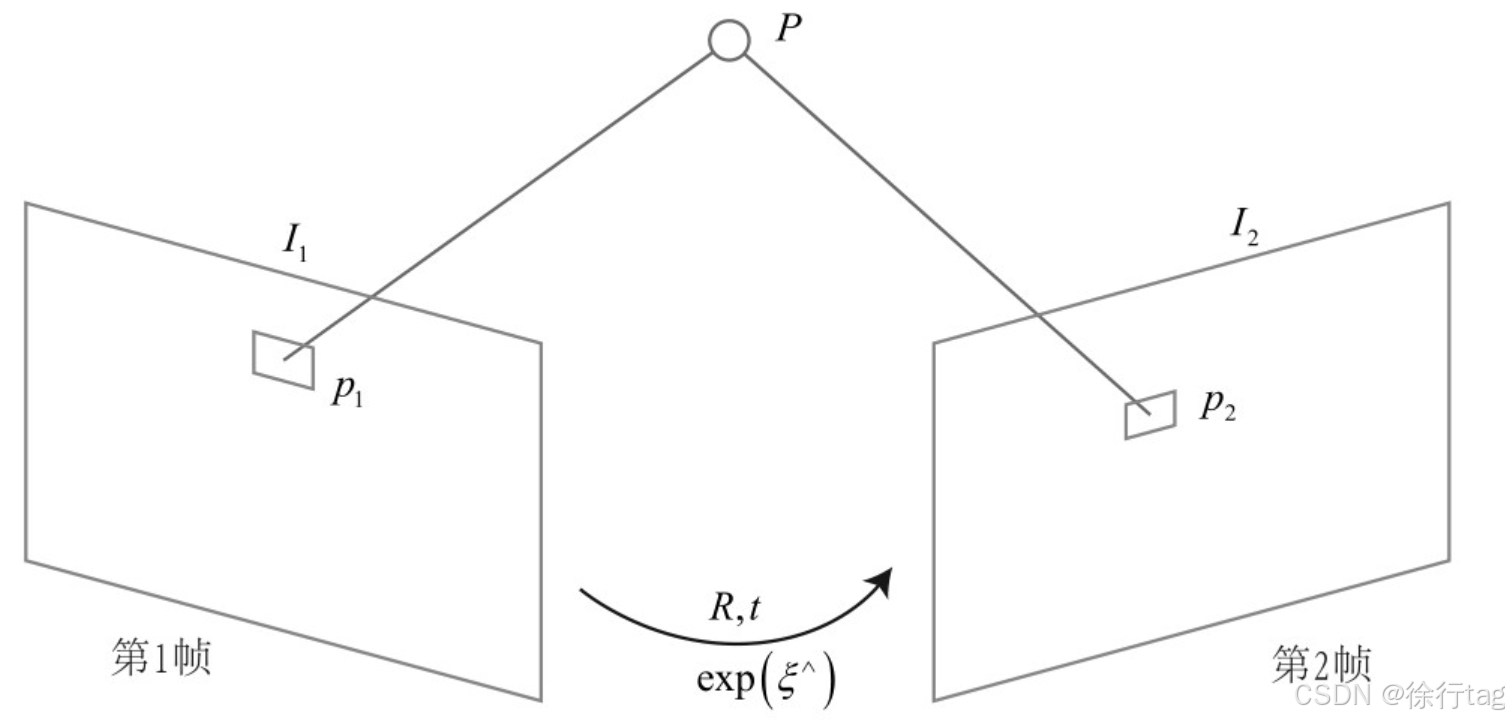
直接法通过最小化相邻图像之间的光度误差来优化位姿参数。以下是推导过程:
1. 问题建模
设参考帧图像为 I ref I_{\text{ref}} Iref,当前帧图像为 I cur I_{\text{cur}} Icur,相机的位姿变换为 T ∈ SE ( 3 ) T \in \text{SE}(3) T∈SE(3),用李代数 ξ ∈ s e ( 3 ) \xi \in \mathfrak{se}(3) ξ∈se(3)参数化。对于参考帧中的每个像素点 p i \mathbf{p}_i pi,其对应的3D点坐标为 P i \mathbf{P}_i Pi,投影到当前帧中的坐标为:
p i ′ = π ( T ⋅ P i ) \mathbf{p}_i' = \pi\left(T \cdot \mathbf{P}_i\right) pi′=π(T⋅Pi)
其中 π \pi π为投影函数, T = exp ( ξ ∧ ) T = \exp(\xi^\wedge) T=exp(ξ∧)。
光度误差定义为:
e i = I cur ( p i ′ ) − I ref ( p i ) e_i = I_{\text{cur}}(\mathbf{p}_i') - I_{\text{ref}}(\mathbf{p}_i) ei=Icur(pi′)−Iref(pi)
则优化目标是最小化总误差:
min ξ ∑ i ∥ e i ∥ 2 \min_\xi \sum_i \| e_i \|^2 ξmini∑∥ei∥2
2. 误差函数的导数
误差关于位姿的雅可比矩阵用链式求导为:
∂ e i ∂ ξ = ∂ I cur ∂ p i ′ ⋅ ∂ p i ′ ∂ ξ \frac{\partial e_i}{\partial \xi} = \frac{\partial I_{\text{cur}}}{\partial \mathbf{p}_i'} \cdot \frac{\partial \mathbf{p}_i'}{\partial \xi} ∂ξ∂ei=∂pi′∂Icur⋅∂ξ∂pi′
(1) 图像梯度项
∂ I cur ∂ p i ′ = [ I x , I y ] \frac{\partial I_{\text{cur}}}{\partial \mathbf{p}_i'} = \left[ I_x, I_y \right] ∂pi′∂Icur=[Ix,Iy]
其中 I x , I y I_x, I_y Ix,Iy 为当前帧在 p i ′ \mathbf{p}_i' pi′处的图像梯度。
(2) 投影点对位姿的导数
投影函数 p i ′ = π ( exp ( ξ ∧ ) P i ) \mathbf{p}_i' = \pi(\exp(\xi^\wedge) \mathbf{P}_i) pi′=π(exp(ξ∧)Pi)的导数为:
∂ p i ′ ∂ ξ = ∂ π ∂ P ′ ⋅ ∂ P ′ ∂ ξ \frac{\partial \mathbf{p}_i'}{\partial \xi} = \frac{\partial \pi}{\partial \mathbf{P}'} \cdot \frac{\partial \mathbf{P}'}{\partial \xi} ∂ξ∂pi′=∂P′∂π⋅∂ξ∂P′
其中:
- P ′ = T ⋅ P i \mathbf{P}' = T \cdot \mathbf{P}_i P′=T⋅Pi为变换后的3D点。
- ∂ π ∂ P ′ \frac{\partial \pi}{\partial \mathbf{P}'} ∂P′∂π为投影函数对3D点的导数:
∂ π ∂ P ′ = [ f x Z ′ 0 − f x X ′ Z ′ 2 0 f y Z ′ − f y Y ′ Z ′ 2 ] \frac{\partial \pi}{\partial \mathbf{P}'} = \begin{bmatrix} \frac{f_x}{Z'} & 0 & -\frac{f_x X'}{Z'^2} \\ 0 & \frac{f_y}{Z'} & -\frac{f_y Y'}{Z'^2} \end{bmatrix} ∂P′∂π=[Z′fx00Z′fy−Z′2fxX′−Z′2fyY′] - ∂ P ′ ∂ ξ \frac{\partial \mathbf{P}'}{\partial \xi} ∂ξ∂P′为李代数扰动模型:
∂ P ′ ∂ ξ = [ I 3 × 3 − P ′ ∧ ] \frac{\partial \mathbf{P}'}{\partial \xi} = \begin{bmatrix} \mathbf{I}_{3\times3} & -\mathbf{P}'^{\wedge} \end{bmatrix} ∂ξ∂P′=[I3×3−P′∧]
其中 P ′ ∧ \mathbf{P}'^{\wedge} P′∧为3D点的反对称矩阵。
3. 雅可比矩阵推导
结合上述结果,雅可比矩阵为:
J i = [ f x Z ′ 0 − f x X ′ Z ′ 2 f x X ′ Y ′ Z ′ 2 − f x ( 1 + X ′ 2 Z ′ 2 ) f x Y ′ Z ′ 0 f y Z ′ − f y Y ′ Z ′ 2 − f y ( 1 + Y ′ 2 Z ′ 2 ) f y X ′ Y ′ Z ′ 2 − f y X ′ Z ′ ] \mathbf{J}_i = \begin{bmatrix} \frac{f_x}{Z'} & 0 & -\frac{f_x X'}{Z'^2} & \frac{f_x X' Y'}{Z'^2} & -f_x\left(1 + \frac{X'^2}{Z'^2}\right) & \frac{f_x Y'}{Z'} \\ 0 & \frac{f_y}{Z'} & -\frac{f_y Y'}{Z'^2} & -f_y\left(1 + \frac{Y'^2}{Z'^2}\right) & \frac{f_y X' Y'}{Z'^2} & -\frac{f_y X'}{Z'} \end{bmatrix} Ji= Z′fx00Z′fy−Z′2fxX′−Z′2fyY′Z′2fxX′Y′−fy(1+Z′2Y′2)−fx(1+Z′2X′2)Z′2fyX′Y′Z′fxY′−Z′fyX′
4. 优化求解
使用高斯-牛顿法迭代更新位姿:
- 计算残差:对每个点计算 e i = I cur ( p i ′ ) − I ref ( p i ) e_i = I_{\text{cur}}(\mathbf{p}_i') - I_{\text{ref}}(\mathbf{p}_i) ei=Icur(pi′)−Iref(pi)。
- 构建雅可比矩阵:按上述公式计算每个点的 J i \mathbf{J}_i Ji。
- 求解增量方程:
H = ∑ i J i T J i , b = − ∑ i J i T e i \mathbf{H} = \sum_i \mathbf{J}_i^T \mathbf{J}_i, \quad \mathbf{b} = -\sum_i \mathbf{J}_i^T e_i H=i∑JiTJi,b=−i∑JiTei
Δ ξ = H − 1 b \Delta \xi = \mathbf{H}^{-1} \mathbf{b} Δξ=H−1b - 更新位姿:
ξ ← ξ + Δ ξ \xi \leftarrow \xi + \Delta \xi ξ←ξ+Δξ
5. 关键点总结
- 光度误差:基于灰度不变假设,直接比较像素亮度。
- 李代数扰动模型:用于计算位姿变化对投影点的影响。
- 雅可比矩阵:结合图像梯度和几何变换导数,指导优化方向。
- 多尺度优化:还可以采用图像金字塔提高鲁棒性和收敛性。
通过迭代优化,直接法能够有效估计相机的位姿变化,适用于特征缺失的场景,但对光照变化和初始值敏感。
至此,关于视觉里程计即根据图像信息求解相机位姿变换的知识已经讲解完毕。接下来将进入后端优化的学习。
相关文章:

直接法估计相机位姿
引入 在前面的文章:运动跟踪——Lucas-Kanade光流中,我们了解到特征点法存在一些缺陷,并且用光流法追踪像素点的运动来替代特征点法进行特征点匹配的过程来解决这些缺陷。而这篇文章要介绍的直接法则是通过计算特征点在下一时刻图像中的位置…...

PHP动态网站建设
如何配置虚拟主机 1. 学习提纲 本地发布与互联网发布:介绍了如何通过本地IP地址和互联网域名发布网站。 虚拟主机配置与访问:讲解了如何配置虚拟主机,并通过自定义域名访问不同的站点目录。 Web服务器配置:详细说明了如何配置A…...

【gRPC】Java高性能远程调用之gRPC详解
gRPC详解 一、什么是gRPC?二、用proto生成代码2.1、前期准备2.2、protobuf插件安装 三、简单 RPC3.1、开发gRPC服务端3.2、开发gRPC客户端3.3、验证gRPC服务 四、服务器端流式 RPC4.1、开发一个gRPC服务,类型是服务端流4.2、开发一个客户端,调…...

数据结构知识学习小结
一、动态内存分配基本步骤 1、内存分配简单示例: 个人对于示例的理解: 定义一个整型的指针变量p(着重认为它是一个“变量”我觉得可能会更好理解),这个变量用来存地址的,而不是“值”,malloc函…...

分布式锁—2.Redisson的可重入锁一
大纲 1.Redisson可重入锁RedissonLock概述 2.可重入锁源码之创建RedissonClient实例 3.可重入锁源码之lua脚本加锁逻辑 4.可重入锁源码之WatchDog维持加锁逻辑 5.可重入锁源码之可重入加锁逻辑 6.可重入锁源码之锁的互斥阻塞逻辑 7.可重入锁源码之释放锁逻辑 8.可重入锁…...

计算机毕业设计SpringBoot+Vue.js球队训练信息管理系统(源码+文档+PPT+讲解)
温馨提示:文末有 CSDN 平台官方提供的学长联系方式的名片! 温馨提示:文末有 CSDN 平台官方提供的学长联系方式的名片! 温馨提示:文末有 CSDN 平台官方提供的学长联系方式的名片! 作者简介:Java领…...
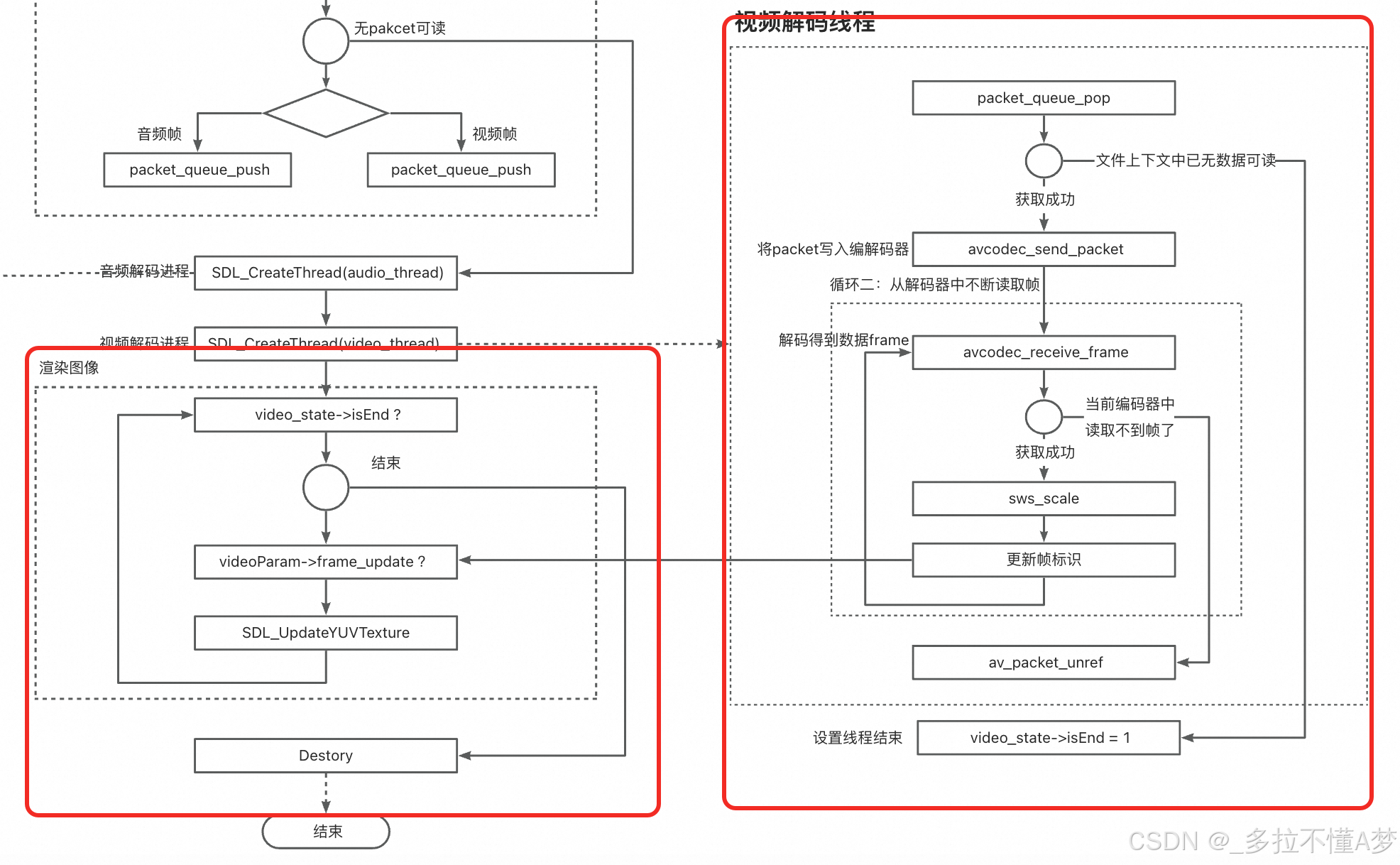
FFmpeg入门:最简单的音视频播放器
FFmpeg入门:最简单的音视频播放器 前两章,我们已经了解了分别如何构建一个简单和音频播放器和视频播放器。 FFmpeg入门:最简单的音频播放器 FFmpeg入门:最简单的视频播放器 本章我们将结合上述两章的知识,看看如何融…...

java 查找两个集合的交集部分数据
利用了Java 8的Stream API,代码简洁且效率高 import java.util.stream.Collectors; import java.util.List; import java.util.HashSet; import java.util.Set;public class ListIntersection {public static List<Long> findIntersection(List<Long> …...
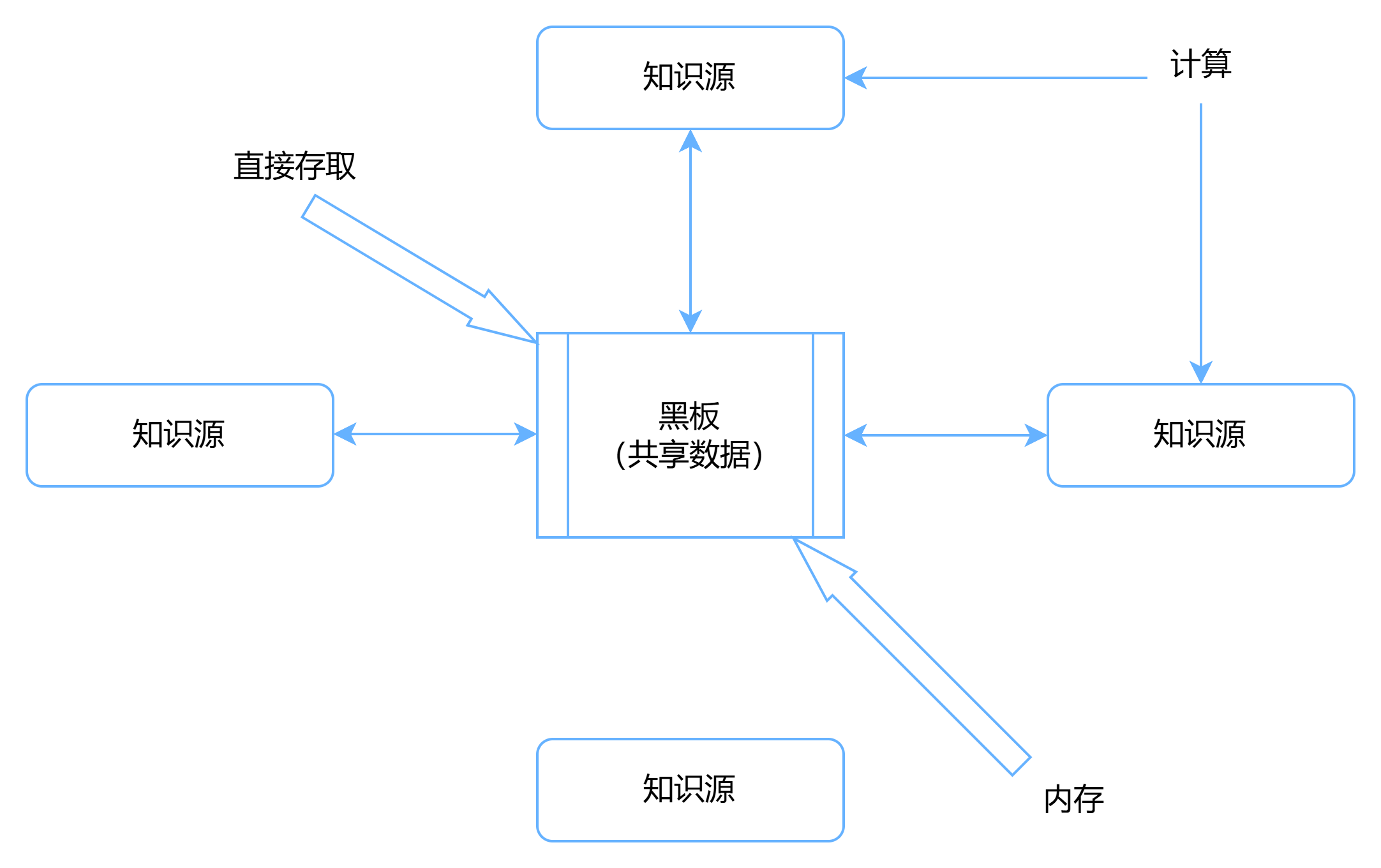
【系统架构设计师】以数据为中心的体系结构风格
目录 1. 说明2. 仓库体系结构风格3. 黑板体系结构风格 1. 说明 1.以数据为中心的体系结构风格主要包括仓库体系结构风格和黑板体系结构风格。 2. 仓库体系结构风格 1.仓库(Repository)是存储和维护数据的中心场所。2.在仓库风格中,有两种不…...
实现自动递增编号的完整解决方案)
通过HTML有序列表(ol/li)实现自动递增编号的完整解决方案
以下是通过HTML有序列表(ol/li)实现自动递增编号的完整解决方案: <!DOCTYPE html> <html> <head> <style> /* 基础样式 */ ol {margin: 1em 0;padding-left: 2em; }/* 方案1:默认数字编号 */ ol.default {list-style-type: dec…...
【Python 数据结构 4.单向链表】
目录 一、单向链表的基本概念 1.单向链表的概念 2.单向链表的元素插入 元素插入的步骤 3.单向链表的元素删除 元素删除的步骤 4.单向链表的元素查找 元素查找的步骤 5.单向链表的元素索引 元素索引的步骤 6.单向链表的元素修改 元素修改的步骤 二、Python中的单向链表 编辑 三…...
指南)
基于 vLLM 部署 LSTM 时序预测模型的“下饭”(智能告警预测与根因分析部署)指南
Alright,各位看官老爷们,准备好迎接史上最爆笑、最通俗易懂的 “基于 vLLM 部署 LSTM 时序预测模型的智能告警预测与根因分析部署指南” 吗? 保证让你笑出猪叫,看完直接变身技术大咖!🚀😂 咱们今天的主题,就像是要打造一个“智能运维小管家”! 这个小管家,不仅能提…...

Java多线程与高并发专题——ConcurrentHashMap 在 Java7 和 8 有何不同?
引入 上一篇我们提到HashMap 是线程不安全的,并推荐使用线程安全同时性能比较好的 ConcurrentHashMap。 而在 Java 8 中,对于 ConcurrentHashMap 这个常用的工具类进行了很大的升级,对比之前 Java 7 版本在诸多方面都进行了调整和变化。不过…...
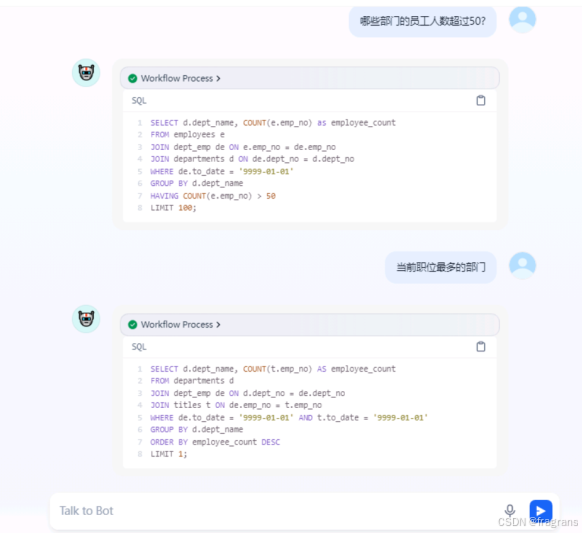
NL2SQL-基于Dify+阿里通义千问大模型,实现自然语音自动生产SQL语句
本文基于Dify阿里通义千问大模型,实现自然语音自动生产SQL语句功能,话不多说直接上效果图 我们可以试着问他几个问题 查询每个部门的员工数量SELECT d.dept_name, COUNT(e.emp_no) AS employee_count FROM employees e JOIN dept_emp de ON e.emp_no d…...

LeetCode 1328.破坏回文串:贪心
【LetMeFly】1328.破坏回文串:贪心 力扣题目链接:https://leetcode.cn/problems/break-a-palindrome/ 给你一个由小写英文字母组成的回文字符串 palindrome ,请你将其中 一个 字符用任意小写英文字母替换,使得结果字符串的 字典…...
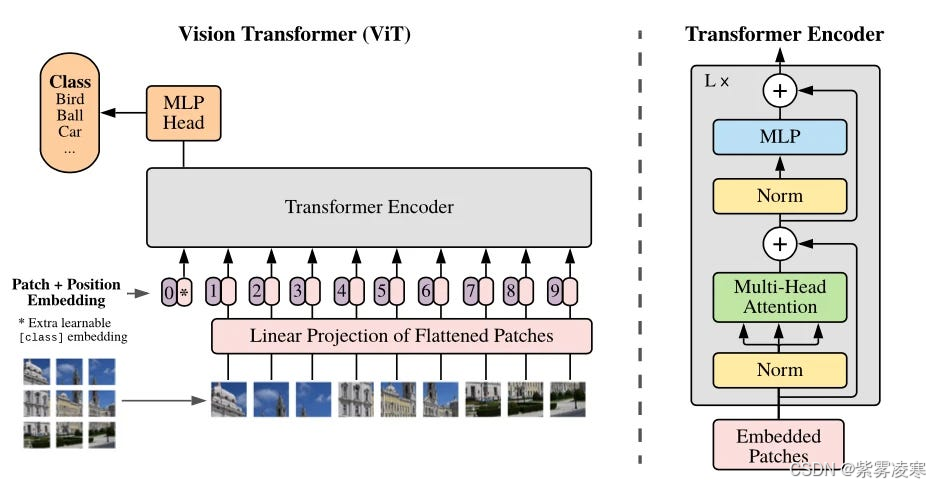
计算机视觉|ViT详解:打破视觉与语言界限
一、ViT 的诞生背景 在计算机视觉领域的发展中,卷积神经网络(CNN)一直占据重要地位。自 2012 年 AlexNet 在 ImageNet 大赛中取得优异成绩后,CNN 在图像分类任务中显示出强大能力。随后,VGG、ResNet 等深度网络架构不…...

//定义一个方法,把int数组中的数据按照指定的格式拼接成一个字符串返回,调用该方法,并在控制台输出结果
import java.util.Scanner; public class cha{ public static void main(String[] args){//定义一个方法,把int数组中的数据按照指定的格式拼接成一个字符串返回,调用该方法,并在控制台输出结果//eg: 数组为:int[] arr…...

Python快捷手册
Python快捷手册 后续会陆续更新Python对应的依赖或者工具使用方法 文章目录 Python快捷手册[toc]1-依赖1-词云小工具2-图片添加文字3-BeautifulSoup网络爬虫4-Tkinter界面绘制5-PDF转Word 2-开发1-多线程和队列 3-运维1-Requirement依赖2-波尔实验室3-Anaconda3使用教程4-CentO…...

QT5 GPU使用
一、问题1 1、现象 2、原因分析 出现上图错误,无法创建EGL表面,错误=0x300b。申请不上native window有可能是缺少libqeglfs-mali-integration.so 这个库 3、解决方法 需要将其adb push 到小机端的/usr/lib/qt5/plugins/egldeviceintegrat…...

如何在Spring Boot中读取JAR包内resources目录下文件
精心整理了最新的面试资料和简历模板,有需要的可以自行获取 点击前往百度网盘获取 点击前往夸克网盘获取 以下是如何在Spring Boot中读取JAR包内resources目录下文件的教程,分为多种方法及详细说明: 方法1:使用 ClassPathResour…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...
