蓝桥备赛（11）- 数据结构、算法与STL

一、数据结构

1.1 什么是数据结构？

在计算机科学中，数据结构是一种   数据组织、管理和存储的格式。它是相互之间存在一种

或多种特定关系的数据元素的集合。

--->  通俗点，数据结构就是数据的组织形式 ， 研究数据是用什么方式存储在存储在g'v计算机中的

1.2 为什么会有数据结构？

1） 随着计算机的发展和应用范围的拓展，计算机需要处理的数据量越来越大，数据类型越来越多，数据之间的关系也越来越复杂。

2）这就要求⼈们对计算机加工处理的数据进行系列的研究，即研究数据的特性、数据之间存在的关系，以及如何有效的组织、管理存储数据， 从而提高计算机处理数据的效率。

1.3 数据结构的三要素

1.3.1 逻辑结构

数据结构：数据中各元素之间的逻辑关系

他只关心数据中各个元素之间的关系 ， 并不关心数据在内存中存储的

1）集合： 所有数据只是放在一个集合中 ， 彼此之间再没有其他联系

2）线性结构：数据之间只存在一对一的关系

3）树：数据之间是一对多的关系

4）图结构：数据之间存在多对多的关系

1.3.2 存储结构

存储结构又称 物理结构 ， 但是存储二字 更能理解 ，后续我们统称为数据结构。

存储结构 顾名思义 ， 就是如何把数据在计算机中存储。

1） 顺序存储：把逻辑上相邻的元素存储在  物理上也相邻的存储单元中  ---> 数组（逻辑、物理上都是连续的）

2）链式存储：逻辑上两个元素相邻 ， 但是物理结构上不一定相邻 

 

1.3.3 数据的运算

数据的运算，（针对数据的各种操作） ， 包括数据结构的实现 ， 以及基于数据结构上的各种操作。

--->   意思是 ， 我们已经知道了一堆数据中  各个元素之间的关系 ， 也知道这堆数据应该在内存中如何存储 。

----> 那么接下来就是写代码 ， 完成我们的需求

二、算法

2.1 什么是算法？

简单来说 --->  算法就是一系列的步骤  ， 用来将输入数据转化为输出结果（用来解决问题）

 

2.2 算法好坏的度量

算法设计好后，根据算法的设计原理，只要问题规模确定，算法中 基本语句执行次数 和 需求资源个数 基本也就确定了。

比如求 1 + 2 + 3 + ... + ( n − 1) + n ，可以设计三种算法：

算法A ： 需要 开辟大小为N 的空间

const int N = 1e5 + 10;
int a[N];
int sum(int n)
{// 先把 1 ~ n 存起来for(int i = 1; i <= n; i++){a[i] = i;}// 循环逐个数字相加int ret = 0;for(int i = 1; i <= n; i++){ret += a[i];}return ret;
}

算法B：不需要开辟空间 ， 直接求和；

int sum(int n)
{// 循环逐个数字相加int ret = 0;for (int i = 1; i <= n; i++) {ret += i;}return ret;
}

算法执行所需资源的个数与问题的规模 n 有关 。因此可以根据算法执行过程中对空间的消耗来衡量算法的好坏 ， 这就是空间复杂度 。

算法C：需要循环 n 次 ， ret += n 语句会执行 n 次 ， 而且随着问题规模的增长 ， 执行次数也会增长 。

int sum(int n)
{int ret = 0;// 循环逐个数字相加for (int i = 1; i <= n; i++) {ret += i;}return ret;
}

 算法D ： 不管问题规模 n 为多少 ， ( 1 + n ) * n / 2 语句只会执行1次。

int sum(int n)
{// 利⽤求和公式return (1 + n) * n / 2;
}

算法中基本语句总的执行次数与问题规模 n 有关 。因此可以根据算法执行过程中 ， 所有语句被执行的次数之和来衡量算法的好坏 ， 这就是时间复杂度 。  

综上所述 ， 时间和空间的消耗情况就是我们度量一个算法好坏的标准 ， 也就是时间复杂度和空间复杂度 。 

2.3 时间复杂度

在计算机中 ， 算法的时间复杂度是一个函数式 T（N）， 他定量描述了该算法的运行时间 。这个T（N）函数式计算了程序中语句的执行次数 。

计算一下 fun 中++count 语句总共执行了多少次 。

void fun(int N) 
{ int count = 0; for(int i = 0; i < N; i++) { for(int j = 0; j < N; j++) { ++count; // 执⾏次数是 n*n，也就是 n^2} } for(int k = 0; k < 2 * N; k++) {++count; // 执⾏次数是 2*n} int M = 10; while(M--) { ++count; // 执⾏次数 10} 
}

 

2.3.1 大O表示法

因此，在计算时间复杂度的时候，一 般会把中对结果影响不大的项忽略掉 ，这种表示时间复杂度的方式称 为大 O 渐进时间复杂度 - 粗略的估计方式 ，只看影响时间开销最大的⼀项。

2.3.2 最优、平均和最差时间复杂度

案例：在 n 个整形元素数组中，检测 x 是否存在，若存在返回其在数组中的下标，否则返回 −1 。

int find (int a[], int n, int x)
{for (int i = 0; i < n; i++){if (a[i] == x) return i;}return -1;
}

1） 在查找过程中，  x 与数组中元素依次比较， 因此总的比较次数就是该算法的时间复杂度。

--->   若待查找元素 x 为 21 ，只需要比较 1 次，为算法的最优(好)情况。

--->   若带查找元素 x 为 17 ，或者是不存在的元素，需要比较 n 次，为算法的最坏(差)情况。

--->   所有情况的比较 次数之和，除以总情况，为算法的平均情况。

无论是在竞赛还是工程中，算法的时间复杂度⼀般为最差情况。 因为最差情况是人对⼀件事情所能承受的底线 ，因此 find 算法的时间复杂度为 O(n ) 。

 

2.3.3 时间复杂度计算案例

案例一：

案例二：

基本语句 ++count 关于问题规模 n 总执行次数的数学表达式为: f ( n ) = 1000 ；

不论 n 如何变化， ++count 总的执行次数都是 1000 ，故时间复杂度为： O(1) 。

 案例三：

void func3(int m, int n)
{for (int i = 0; i < m; i++){printf("hello\n");}for (int i = 0; i < n; i++){printf("hello\n");}
}

基本语句 printf("") 总的执行次数为 f(m, n) = m + n ；

m 和 n 的变化都是影响基本语句执行次数， 即m  和 n 都是问题规模， 故时间复杂度为

O ( m + n ) ， 或者也可以表示为 O(max（m,n)) 。  

案例四：

 基本语句 printf("") 总的执行次数为 f(m, n) = m x n ；

m 和 n 的变化都是影响基本语句执行次数， 即m  和 n 都是问题规模， 故时间复杂度为

O ( m x   n )

案例5：

void func5(int n)
{int cnt = 1;while (cnt < n){cnt *= 2;}
}

案例六：

递归算法时间复杂度求解方式为，单次递归时间 × 总的递归次数。

注意，这里只是简易的估算方式。递归算法的时间复杂度严谨的计算方法是 利用主定理 (Master Theorem)来求得递归算法的时间复杂度 。

                                               O( n )

 

2.4 空间复杂度

在算法竞赛中，空间复杂度就是整个程序在解决这个问题时， ⼀共使用了多少空间。相比较于时间复杂度，空间复杂度就没那么受关注，因为多数情况下题目所给的内存限制是非常宽裕的。 但是，这并不表明可以肆无忌惮的使用空间，一旦超出给定的限制，程序也是不会通过的。 - MLE

案例一：冒泡排序 

#include <iostream>
using namespace std;const int N = 20;
int arr[N];int main(){int n = 0;cin >> n;int i = 0;//输入 for(i=0; i < n; i++)cin >> arr[i];//排序for(i = 0; i < n-1; i++){int j = 0;for(j = 0; j <= n-1-i; j++){if(arr[j] < arr[j+1]){int tmp = arr[j];arr[j] = arr[j+1];arr[j+1] = tmp; }}} //输出for(i=0; i < n; i++){cout << arr[i] << endl;}return 0;}

案例二：递归求阶乘

 

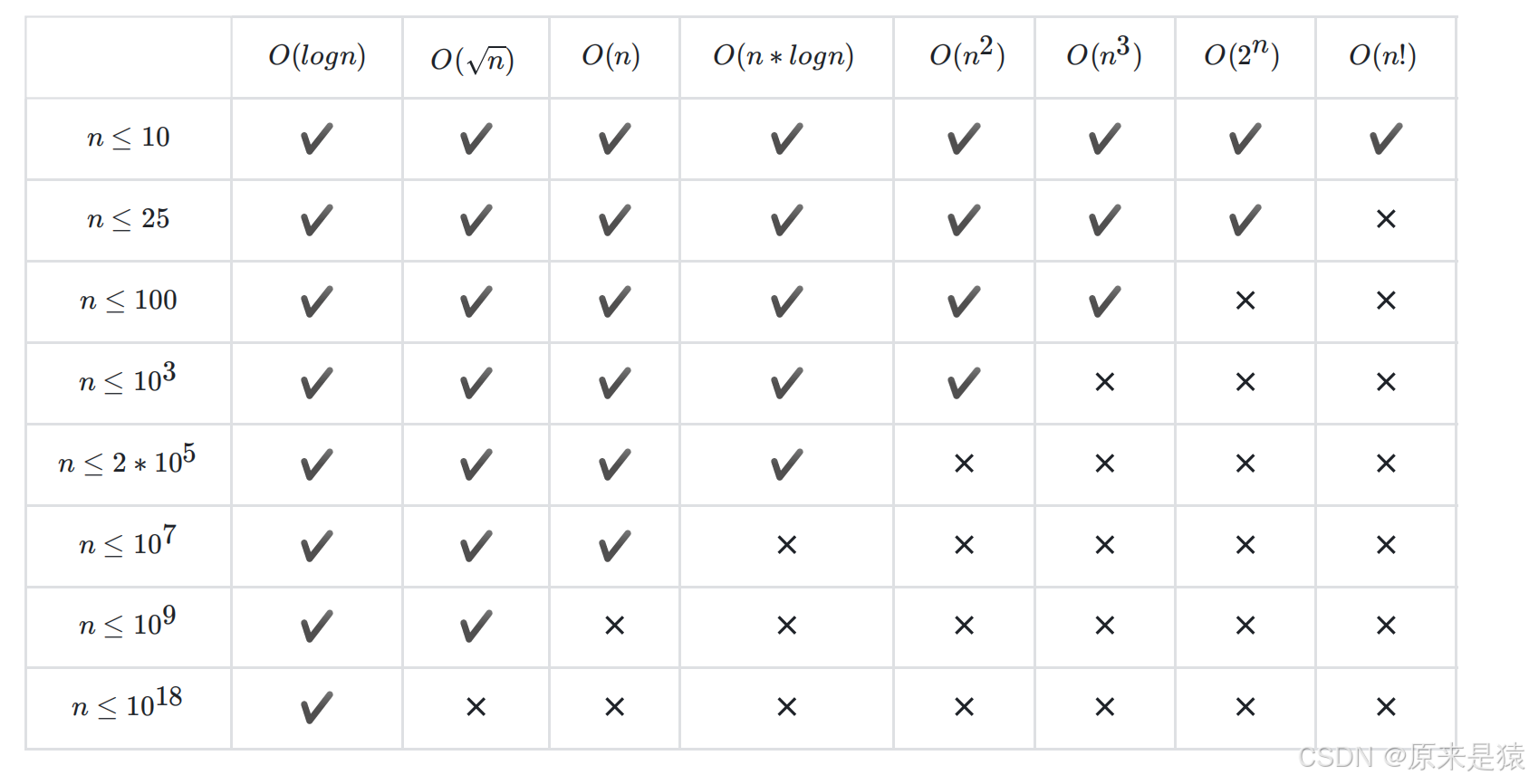
2.5 常见复杂度的增长对比

 

2.6 算法中的时间和空间限制

1. 信息学竞赛中，C++ 通常设定 1 到 2 秒的时间限制，运行次数在 10^7 ⾄ 10^8 之间。

2.空间限制在128MB 或 256MB ，可以开⼀个3 x 10 ^7 大小的int  类型数组，或者5000x5000大小的二维数组，⼀般情况下都是够⽤的。

各种数据量下，可选用的算法的时间复杂度：

三、STL

3.1 C++标准库

1） C++标准是C++编程语言的规范，由国际标准化组织（ISO）制定。C++标准的发展历程可以追溯到 1998年，当时ISO/IEC 14882:1998标准被发布，这是第⼀个C++标准，常被称为C++98。随后，C++标准经历了多次更新和修订，包括C++03（2003年）、C++11（2011年）、C++14（2014年）、C++17（2017年）以及 C++20。

2）最新的C++标准是C++23，于2023年发布，引入了许多新特性， 但目前完整的编译器较少。

3）每⼀个版本的 C++ 标准不仅规定了 C++ 的语法、语言特性，还规定了⼀套 C++ 内置库的实现规范，这个库便是 C++ 标准库。C++ 标准库中包含大量常用代码的实现，如输入输出、基本数据结构、内存管理、多线程支持等。

4）我们可以这样简单的理解，C++ 给我们提供了一大堆的代码，这些代码里面包含特别多已经实现好的   数据结构 和 算法 。 因此，在做题的时候，如果涉及的数据结构和算法 C++ 标准库已经帮我们实现好 了，那么就可以直接使用，避免重复造轮子 。 --- sort / min / max / swap

1） 造轮子指的是重复发明已有的算法，或者重复编写现成优化过的代码。

2）造轮子通常耗时好力，同时效果还没有别人好。但若是为了学习或者练习，造轮子则是必要的。

因此，学好 C++ 标准库能极大的提高编程效率。

3.2 什么是STL？

STL 即标准模板库（Standard Template Library），是 C++ 标准库的一部分， 里面包含了⼀些模板化的通过用的数据结构和算法 。由于其模板化的特点，它能够兼容自定义的数据类型，避免大量的造轮子工作。

NOI 和 ICPC 赛事都支持 STL 库的使用，当然， 蓝桥杯也是支持的 。因此，⼀定要学习 STL 的使用， 能够极大的提高编写代码的效率。

3.3 怎么学习STL？

模范使用！！！ STL 的实现涉及比较⾼深的 C++ 知识， 比如类、模板、容器适配器等 。如果想 搞清楚背后的原理，就必须要学会这些知识。但是这些知识在竞赛中是用不到的，如果深究，会浪费

大量无用的时间。因此，目前先把重点放在如何使用上。