Embedding技术:DeepWalkNode2vec
引言
在推荐系统中,Graph Embedding技术已经成为一种强大的工具,用于捕捉用户和物品之间的复杂关系。本文将介绍Graph Embedding的基本概念、原理及其在推荐系统中的应用。
什么是Graph Embedding?
Graph Embedding是一种将图中的节点映射到低维向量空间的技术。通过这种映射,图中的节点可以在向量空间中表示为密集的向量,从而方便进行各种机器学习任务,如分类、聚类和推荐。

Graph Embedding的基本原理
1. 图的表示
一个图 G = ( V , E ) G = (V, E) G=(V,E)由节点集合 V V V和边集合 E E E组成。在推荐系统中,节点可以表示用户或物品,边可以表示用户与物品之间的交互(如点击、购买等)。图可以是有向的或无向的,也可以是加权的(例如,边权重表示交互的强度)。
2. 目标函数
Graph Embedding的目标是学习一个映射函数 f : V → R d f: V \rightarrow \mathbb{R}^d f:V→Rd,将每个节点 v ∈ V v \in V v∈V映射到一个 d d d维的向量空间。这个映射函数通常通过优化以下目标函数来学习:
min f ∑ ( u , v ) ∈ E L ( f ( u ) , f ( v ) ) \min_{f} \sum_{(u, v) \in E} \mathcal{L}(f(u), f(v)) fmin(u,v)∈E∑L(f(u),f(v))
其中, L \mathcal{L} L是损失函数,用于衡量节点 u u u和 v v v在向量空间中的相似性。常见的损失函数包括:
-
负对数似然损失:
L ( f ( u ) , f ( v ) ) = − log σ ( f ( u ) T f ( v ) ) \mathcal{L}(f(u), f(v)) = -\log \sigma(f(u)^T f(v)) L(f(u),f(v))=−logσ(f(u)Tf(v))
其中, σ ( x ) = 1 1 + e − x \sigma(x) = \frac{1}{1 + e^{-x}} σ(x)=1+e−x1是sigmoid函数。 -
欧氏距离损失:
L ( f ( u ) , f ( v ) ) = ∥ f ( u ) − f ( v ) ∥ 2 2 \mathcal{L}(f(u), f(v)) = \|f(u) - f(v)\|_2^2 L(f(u),f(v))=∥f(u)−f(v)∥22
目标函数的核心思想是:如果两个节点在图中是相邻的(即存在边),那么它们在向量空间中的表示应该尽可能相似。
3. 常见的Graph Embedding方法
3.1 DeepWalk
DeepWalk是一种基于随机游走的Graph Embedding方法。它通过在图中进行随机游走,生成节点序列,然后使用Skip-gram模型来学习节点的向量表示。Skip-gram原理可以我前几篇Embedding生成文章

DeepWalk
给定一个起始节点 v i v_i vi,随机游走生成一个节点序列 v i 1 , v i 2 , … , v i k v_{i1}, v_{i2}, \dots, v_{ik} vi1,vi2,…,vik,其中每个节点 v i j v_{ij} vij是从当前节点 v i ( j − 1 ) v_{i(j-1)} vi(j−1)的邻居中随机选择的。(如上图所示)
Skip-gram模型
Skip-gram模型的目标是最大化给定中心节点 v i v_i vi时,其上下文节点 v i − w , … , v i + w v_{i-w}, \dots, v_{i+w} vi−w,…,vi+w的条件概率。目标函数为:
min f − log P ( v i − w , … , v i + w ∣ f ( v i ) ) \min_{f} -\log P(v_{i-w}, \dots, v_{i+w} \mid f(v_i)) fmin−logP(vi−w,…,vi+w∣f(vi))
具体地,Skip-gram模型使用softmax函数来计算条件概率:
P ( v j ∣ v i ) = exp ( f ( v j ) T f ( v i ) ) ∑ v k ∈ V exp ( f ( v k ) T f ( v i ) ) P(v_j \mid v_i) = \frac{\exp(f(v_j)^T f(v_i))}{\sum_{v_k \in V} \exp(f(v_k)^T f(v_i))} P(vj∣vi)=∑vk∈Vexp(f(vk)Tf(vi))exp(f(vj)Tf(vi))
由于直接计算softmax的分母计算量较大,通常采用负采样(Negative Sampling)来近似计算。负采样的目标函数为:
min f − log σ ( f ( v j ) T f ( v i ) ) − ∑ k = 1 K E v k ∼ P n ( v ) log σ ( − f ( v k ) T f ( v i ) ) \min_{f} -\log \sigma(f(v_j)^T f(v_i)) - \sum_{k=1}^K \mathbb{E}_{v_k \sim P_n(v)} \log \sigma(-f(v_k)^T f(v_i)) fmin−logσ(f(vj)Tf(vi))−k=1∑KEvk∼Pn(v)logσ(−f(vk)Tf(vi))
其中, K K K是负采样数, P n ( v ) P_n(v) Pn(v)是负采样分布。
3.2 Node2Vec
Node2Vec是对DeepWalk的改进,它引入了广度优先搜索(BFS)和深度优先搜索(DFS)的策略,可以更好地捕捉图的局部和全局结构。

随机游走策略

Node2Vec的随机游走策略由两个参数控制,以使Embedding结果倾向于同质化(距离相近节点Embedding相似)或结构性(结构上相似节点Embedding应相似):
- 返回参数 p p p:控制游走返回到前一个节点的概率。
- 进出参数 q q q:控制游走远离前一个节点的概率。
具体地,Node2Vec的随机游走概率定义为:
P ( v j ∣ v i ) = { 1 p if d i j = 0 1 if d i j = 1 1 q if d i j = 2 P(v_j \mid v_i) = \begin{cases} \frac{1}{p} & \text{if } d_{ij} = 0 \\ 1 & \text{if } d_{ij} = 1 \\ \frac{1}{q} & \text{if } d_{ij} = 2 \end{cases} P(vj∣vi)=⎩ ⎨ ⎧p11q1if dij=0if dij=1if dij=2
其中, d i j d_{ij} dij是节点 v i v_i vi和 v j v_j vj之间的最短路径距离。
结构性和同质性
在node2vec算法中,通过精心调整p和q参数,可以巧妙地引导节点嵌入(Embedding)的方向,使其呈现出不同的特性。具体而言:
-
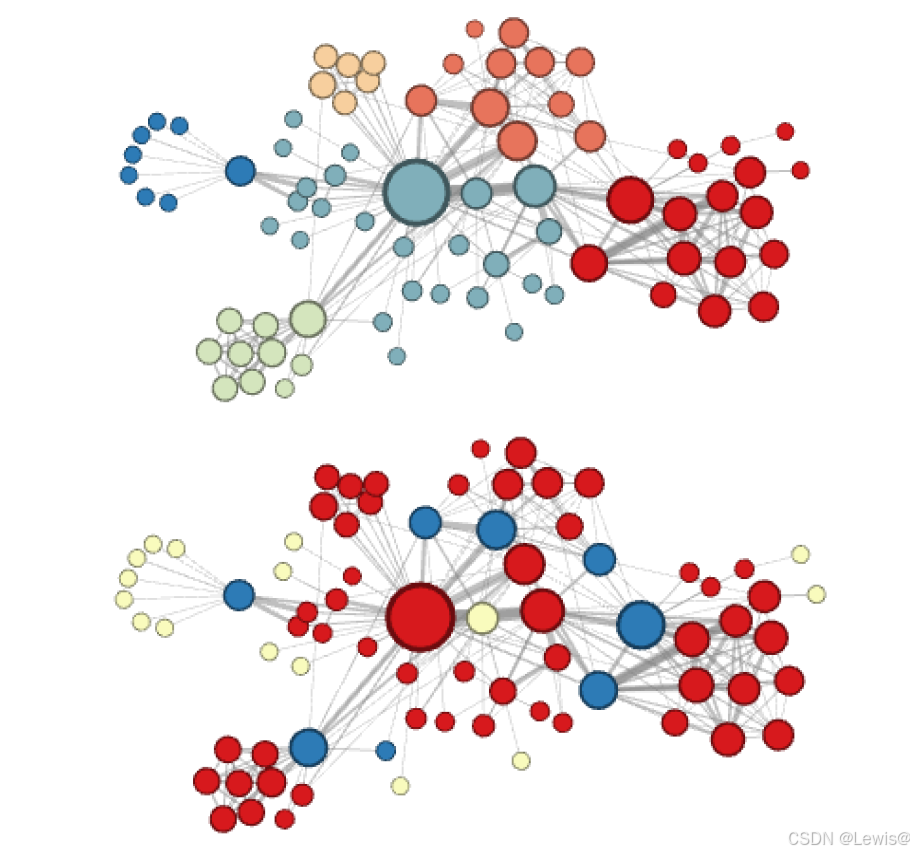
若我们对网络节点的局部特征更为关注,倾向于让相近的节点在嵌入空间中具有相似的表示,那么可通过调整参数使节点Embedding更倾向于同质性,例如上图所示的网络节点Embedding情况;
-
反之,若我们更重视网络的全局结构特征,希望结构相近的节点在嵌入空间中能够彼此靠近,即使它们在实际网络中可能相隔较远,那么就可以像下图那样,使节点Embedding更倾向于结构性。这种灵活的参数调节机制,使得node2vec算法能够根据不同的任务需求和数据特点,生成更符合需求的节点嵌入表示,为后续的图分析和机器学习任务提供了强大的特征支持。
目标函数
Node2Vec的目标函数与DeepWalk类似,但随机游走的策略更加灵活,能够更好地捕捉图的结构信息。目标函数为:
min f − log P ( v i − w , … , v i + w ∣ f ( v i ) ) \min_{f} -\log P(v_{i-w}, \dots, v_{i+w} \mid f(v_i)) fmin−logP(vi−w,…,vi+w∣f(vi))
Graph Embedding在推荐系统中的应用
1. 用户-物品图
在推荐系统中,用户与物品之间的交互行为(如点击、购买、评分等)可以自然地建模为一个用户-物品二分图(User-Item Bipartite Graph)。该图 G = ( V , E ) G = (V, E) G=(V,E) 中,节点集合 V V V 分为两部分:用户节点 U U U 和物品节点 I I I,边集合 E E E 表示用户与物品之间的交互。例如,边 ( u , i ) (u, i) (u,i) 表示用户 u u u 与物品 i i i 的交互行为,边的权重可以表示交互的强度(如点击次数或评分值)。
通过Graph Embedding技术,用户和物品可以被映射到同一个低维向量空间 R d \mathbb{R}^d Rd,从而将复杂的图结构转化为稠密的向量表示。这种表示不仅保留了用户与物品之间的显式交互关系,还能够捕捉隐式的高阶关系(如用户之间的相似性或物品之间的关联性)。
2. 推荐算法
基于Graph Embedding的推荐算法通常包括以下步骤:
-
构建用户-物品图
根据用户与物品的交互数据构建二分图,明确节点和边的定义及其权重。 -
学习用户和物品的向量表示
使用Graph Embedding方法(如DeepWalk、Node2Vec等)将用户和物品映射到低维向量空间,得到向量表示 f ( u ) f(u) f(u) 和 f ( i ) f(i) f(i)。 -
计算相似性并生成推荐列表
对于目标用户 u u u,计算其向量 f ( u ) f(u) f(u) 与所有物品向量 f ( i ) f(i) f(i) 的相似性(如余弦相似度或点积),并根据相似性得分对物品排序,生成个性化推荐列表。
3. 优势
基于Graph Embedding的推荐系统具有以下显著优势:
-
捕捉复杂关系
Graph Embedding能够捕捉用户与物品之间的高阶相似性和隐式反馈。例如,通过随机游走或邻居聚合,可以发现用户之间或物品之间的潜在关联,从而提升推荐的准确性。 -
可扩展性
基于Graph Embedding的方法通常具有较高的可扩展性,能够处理大规模的用户-物品交互数据。例如,GraphSAGE通过邻居采样和聚合机制,降低了计算复杂度,适用于大规模图数据。 -
灵活性
Graph Embedding方法可以与其他推荐技术(如矩阵分解、深度学习等)结合,进一步提升推荐性能。例如,可以将Graph Embedding生成的向量作为输入特征,用于深度学习模型的训练。 -
冷启动问题的缓解
通过捕捉用户与物品之间的高阶关系,Graph Embedding能够为冷启动用户或物品提供更合理的推荐,缓解冷启动问题。
Reference
- 王喆《深度学习推荐系统》
- Perozzi, B., Al-Rfou, R., & Skiena, S. (2014). DeepWalk: Online Learning of Social Representations. Stony Brook University Department of Computer Science.
- Grover, A., & Leskovec, J. (2016). node2vec: Scalable Feature Learning for Networks. Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.
相关文章:

Embedding技术:DeepWalkNode2vec
引言 在推荐系统中,Graph Embedding技术已经成为一种强大的工具,用于捕捉用户和物品之间的复杂关系。本文将介绍Graph Embedding的基本概念、原理及其在推荐系统中的应用。 什么是Graph Embedding? Graph Embedding是一种将图中的节点映射…...

微信小程序注册组件
在微信小程序中注册组件分为自定义组件的创建和全局/局部注册,下面为你详细介绍具体步骤和示例。 自定义组件的创建 自定义组件由四个文件组成,分别是 .js(脚本文件)、.json(配置文件)、.wxml(…...

【docker】安装mysql,修改端口号并重启,root改密
我的docker笔记 【centOS】安装docker环境,替换国内镜像 1. 配置镜像源 使用阿里云镜像加速器,编辑/etc/docker/daemon.json sudo mkdir -p /etc/docker sudo tee /etc/docker/daemon.json <<-EOF {"registry-mirrors": ["https:/…...

自定义wordpress三级导航菜单代码
首先,在你的主题functions.php文件中,添加以下代码以注册一个新的菜单位置: function mytheme_register_menus() {register_nav_menus(array(primary-menu > __(Primary Menu, mytheme))); } add_action(init, mytheme_register_menus); …...

洛谷 P1480 A/B Problem(高精度详解)c++
题目链接:P1480 A/B Problem - 洛谷 1.题目分析 1:说明这里是高精度除以低精度的形式,为什么不是高精度除以高精度的形式,是因为它很少见,它的模拟方式是用高精度减法来做的,并不能用小学列竖式的方法模拟…...

JAVA入门——网络编程简介
自己学习时的笔记,可能有点水( 以后可能还会补充(大概率不会) 一、基本概念 网络编程三要素: IP 设备在网络中的唯一标识 端口号 应用软件在设备中的唯一标识两个字节表示的整数,0~1023用于知名的网络…...

Ubuntu 合上屏幕 不待机 设置
有时候需要Ubuntu的机器合上屏幕的时候也能正常工作,而不是处于待机状态。 需要进行配置文件的设置,并重启即可。 1. 修改配置文件 /etc/systemd/logind.conf sudo vi /etc/systemd/logind.conf 然后输入i,进入插入状态,修改如…...

捣鼓180天,我写了一个相册小程序
🙋为什么要做土著相册这样一个产品? ➡️在高压工作之余,我喜欢浏览B站上的熊猫幼崽视频来放松心情。有天在家族群里看到了大嫂分享的侄女卖萌照片,同样感到非常解压。于是开始翻阅过去的聊天记录,却发现部分图片和视…...

短分享-Flink图构建
一、背景 通过简单的书写map、union、keyby等代码,Flink便能构建起一个庞大的分布式计算任务,Flink如何实现的这个酷炫功能呢?我们本次分享Flink做的第一步,将代码解析构建成图 源码基于Flink 2.10,书籍参考《Flink核…...

【监督学习】支持向量机步骤及matlab实现
支持向量机 (四)支持向量机1.算法步骤2. MATLAB 实现参考资料 (四)支持向量机 支持向量机(Support Vector Machine, SVM)是一种用于分类、回归分析以及异常检测的监督学习模型。SVM特别擅长处理高维空间的…...

机器学习-随机森林解析
目录 一、.随机森林的思想 二、随机森林构建步骤 1.自助采样 2.特征随机选择 3构建决策树 4.集成预测 三. 随机森林的关键优势 **(1) 减少过拟合** **(2) 高效并行化** **(3) 特征重要性评估** **(4) 耐抗噪声** 四. 随机森林的优缺点 优点 缺点 五.…...

Javaweb后端spring事务管理 事务四大特性ACID
2步操作,只能同时成功,同时失败,要放在一个事务中,最后提交事务或者回滚事务 事务控制 事务管理进阶 事务的注解 这是所有异常都会回滚 事务注解 事务的传播行为 四大特性...

在Spring Boot + MyBatis中优雅处理多表数据清洗:基于XML的配置化方案
问题背景 在实际业务中,我们常会遇到数据冗余问题。例如,一个公司表(sys_company)中存在多条相同公司名的记录,但只有一条有效(del_flag0),其余需要删除。删除前需将关联表…...

【无标题】四色拓扑模型与宇宙历史重构的猜想框架
### 四色拓扑模型与宇宙历史重构的猜想框架 --- #### **一、理论基础:四色拓扑与时空全息原理的融合** 1. **宇宙背景信息的拓扑编码** - **大尺度结构网络**:将星系团映射为四色顶点,纤维状暗物质结构作为边,构建宇宙尺度…...

[特殊字符] Django 常用命令
🚀 Django 常用命令大全:从开发到部署 Django 提供了许多实用的命令,可以用于 数据库管理、调试、测试、用户管理、运行服务器、部署 等。 本教程将详细介绍 Django 开发中最常用的命令,并提供 示例,帮助你更高…...

mysql中如何保证没有幻读发生
在 MySQL 中,幻读(Phantom Read)是指在一个事务中,两次相同的查询返回了不同的结果集,通常是由于其他事务插入或删除了符合查询条件的数据。为了保证没有幻读,MySQL 主要通过 事务隔离级别 和 锁机制 来实现…...

Golang实践录:go发布版本信息收集
go发布版本信息收集。 背景 本文从官方、网络资料收罗有关go的发布历史概况。主要目的是能快速了解golang不同版本的变更。鉴于官方资料为英文,为方便阅读,使用工具翻译成中文,重要特性参考其它资料补充/修改。由于发布版本内容较多…...

字节跳动AI原生编程工具Trae和百度“三大开发神器”AgentBuilder、AppBuilder、ModelBuilder的区别是?
字节跳动AI编程工具Trae与百度"三大开发神器"(AgentBuilder、AppBuilder、ModelBuilder)在定位、功能架构和技术路线上存在显著差异,具体区别如下: 一、核心定位差异 Trae:AI原生集成开发环境(AI…...

【UCB CS 61B SP24】Lecture 21: Data Structures 5: Priority Queues and Heaps 学习笔记
本文介绍了优先队列与堆,分析了最小堆的插入与删除过程,并用 Java 实现了一个通用类型的最小堆。 1. 优先队列 1.1 介绍 优先队列是一种抽象数据类型,其元素按照优先级顺序被处理。不同于普通队列的先进先出(FIFO)&…...

mapbox高阶,结合threejs(threebox)添加三维球体
👨⚕️ 主页: gis分享者 👨⚕️ 感谢各位大佬 点赞👍 收藏⭐ 留言📝 加关注✅! 👨⚕️ 收录于专栏:mapbox 从入门到精通 文章目录 一、🍀前言1.1 ☘️mapboxgl.Map 地图对象1.2 ☘️mapboxgl.Map style属性1.3 ☘️threebox Sphere静态对象二、🍀使用t…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...
