第十五届蓝桥杯----B组cpp----真题解析(小白版本)
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档
文章目录
- 必看前言!!!!!
- 一、试题A:握手问题
- 1.题意分析
- 2.代码解答
- 二、试题B:小球反弹
- 1.题意分析
- 2.代码解答
- 3.关键点分析
- 三、试题C:好数
- 1.注意事项!
- 2.题意分析
- 3.代码解答
- 四、试题D:R格式
- 1.备注!!!!
- 2.题意分析
- 3.个人思路解析
- 4.代码解答
- 五、试题F:数字接龙
- 1.备注!!!!
- 2.题意分析
- 3.个人思路解析
- 5.代码解答
- 六、试题H:拔河(原省赛最后一题)
- 1.备注
- 2.题目
- 3.知识点说明
- 4.思路分析
- 5.代码解答
- 6.注意点
- 七、试题E: 宝石组合
- 八、试题G: 爬山
- 总结
必看前言!!!!!
今天来解析一波蓝桥杯真题,我会用我自己小白的视角去解析每一道题,都是自己的亲身写题过程
以下题目少部分顺序不是官方比赛顺序,我会进行标注
注意!!!: 题目如果需要某些算法和知识点,我会提前标注出来,请先学习后再看我的题解,我不会讲解此知识点!!!!!!
题目肯定会有多种解答,以下思路仅为个人思路,有更好的思路的话请沿用自己的思路,本人题解思路仅供参考!!!!
一、试题A:握手问题

1.题意分析
这题我们直接暴力解答就行,因为只需要提交一个答案,相当于没有时间限制
所以我们怎么暴力怎么来
我们直接暴力for遍历每一个人能够与哪些人握手,但这题有个关键点
注意 A 和 B 握手的同时也意味着 B 和 A 握手了,所以算作是一次握手
所以意味着我们在用两个for遍历的时候,第二层for起点必须是第一层for的下一个人
2.代码解答
#include<iostream>
using namespace std;
int ans=0;//总共握手多少次
int main()
{for(int i=8;i<50;i++)//从第八个人开始 每个人都能与其他人握手{for(int j=i+1;j<=50;j++){ans++;}}ans+=7*43;//这七个人可以分别与另外43个人握一次手cout<<ans;return 0;
}
第一层for表示的是每个人,我们从第8个人开始,这是因为有7个人是不能相互握手的,所以我们先不统计他们的握手次数,注意,第一层for不能遍历到最后一个人,因为前面所有人与最后一人握手,导致最后一人的握手情况已经加了一次了
最后我们直接统计这7个人的握手情况就行,因为这7个人分别能与剩下的43人握手,所以直接7*43
二、试题B:小球反弹

1.题意分析
我当时这题也没写出来,现在我们一起来分析一下思路,其实这题不难
我们先假设,如果是一个正方形,并且以45°角出发,第一次碰到边界中点
那么第一次回到左上角应该是这样的运动轨迹
红色表示出发,绿色表示返回的形成

-------------------------紫色d-------蓝色d
此时的总路程为(d+d)+(d+d)=4d 一来一回
那么如果我们把这个正方形一直延展呢?
是不是会变成这样
红色还是表示第一张图的出发路径,绿色表示返回的路径

是不是 恍然大悟?我们并不需要一直反弹,我们只需要一直向下走,直到到达右下角就行!!!!!那么这里的 总路程为 (d+d)+(d+d)=4d
那么现在问题转换为什么时候会到达右下角?
题目中说了dx与dy的速率之比为15:17
然后知道速率之比为15:17 那么路程之比dx:dy也为15:17
所以我们这里暴力枚举就行,没一秒,dx走15,dy走17,什么时候同时满足dx可以整除343710和dy可以整除233333的时候,就到达了右下角
但是还有一个最重要的关键点别忘记了!!!
我们这里求的路程出发的时候是d要变成2d,返回的路径为d,也要变成2d
2.代码解答
#include<iostream>
#include<algorithm>
#include<iomanip>
using namespace std;
typedef long long ll;
ll dx=0;
ll dy=0;
long double sum=0;
int main()
{while(1){dx+=15;dy+=17;if(dx%343720==0&&dy%233333==0)break;}cout << setprecision(2) << fixed <<sqrt(2*dy*2*dy+2*dx*2*dx);return 0;
}
3.关键点分析
关于最后的dy变成2倍,dx变成2倍,可能有人不理解
因为我们现在求出来的dx和dy是总路程为2d的时候的dx和dy,但总路程是4d不是2d,当斜边*2以后,两条直角边都要 *2
那我就画个图来表示一下

到这我们就成功拿下两道填空题啦!!!!鼓掌!
三、试题C:好数


1.注意事项!
当我们拿到一道非填空题的时候,首先看题,其次最重要的就是看这个评测用例规模与约定
总结为一句话
当你的程序在保证对的情况下并且使用c++打竞赛,如果到达10的8次方的复杂度,此程序可能会超时
那么当到达10的9次方的时候,此程序必超时
2.题意分析
其实也没啥好分析的,题目已经说的很简单了,就一个个奇偶判断就行,下面我直接上代码
3.代码解答
#include<iostream>
#include<algorithm>
using namespace std;
int n;
int ans=0;//记录好数的个数bool check(int num)
{bool flag=1;//奇数为真 偶数维假//我们一开始将flag设置为真while(num!=0)//依次遍历num的每一位数{int t=num%10;num/=10;//将这一位丢弃//当奇数位的数为偶数if(flag&&t%2==0)return false;//当偶数位的数为奇数if(!flag&&t%2!=0)return false;flag=!flag;//更新}return true;//前面都没有返回false 说明是好数 直接return true
}int main()
{cin>>n;for(int i=1;i<=n;i++){if(check(i)){ans++;}}cout<<ans;return 0;
}
四、试题D:R格式

1.备注!!!!
这题说白了就是一个高精度*单精度的板子题目,看我的这篇题解前请先学会此知识点!
2.题意分析
这里意思就是给一个浮点数d,然后让这个d去乘n个2,然后得到一个四舍五入的整数,这就是题目要我们做的事情,但我们看评测范围,n最大有1000,那我请问你,2的1000次方,long long能装的下吗?????显然不能啊,单从这点我们就可以立马想到,要用高精度,既然要用高精度,是不是要用字符串呢???
这题我们可以用高精度*高精度,就是用字符串表示2的n次方,然后用字符串表示这个d,但完全没必要!!!!!!
我们直接用高精度*单精度即可,第一因为简单一点,第二也不会超时,因为最多就1000个2,每次让d*2,也就1000次,根本不会超时
3.个人思路解析
首先将浮点数d用字符串存储,然后将字符串反转后存入数组中(如果这里要问为什么反转存入,说明你没懂高精度乘法,回去学完再往下看)
然后用for依次高精度*2
用一个dex记录小数点的位置,这样在最后四舍五入的时候就只判断小数点后的那位数就行
大致思路就这样
主要注意点就是len长度的更新还有进位
下面我直接上代码,我在代码中每一步都做了详细说明
4.代码解答
#include<iostream>
#include<algorithm>
using namespace std;
int n,arr[1000005],len,dex;//len是当前数的总长度 dex记录小数点位置
string d;void kkkk()
{for(int i=1;i<=len;i++)//注意这里是 <=len 注意细节噢{//每一位依次*2arr[i]*=2;}//考虑进位for(int i=1;i<=len;i++)//注意这里是 <=len 注意细节噢{arr[i+1]+=arr[i]/10;arr[i]%=10;}if(arr[len+1])//一开始这个值是0 因为我们是全局变量默认为0 如果不是0说明进位导致位数变大{len++;//所以要更新长度}
}int main()
{cin>>n>>d;//将字符串反转 便于存入arr数组中进行高精度乘法reverse(d.begin(),d.end());dex=d.find('.');//此时dex下标为小数点的下标位置 但需要注意的是此下标是从0开始数的d.erase(dex,1);//将小数点删除 便于存入arr中//dex++;//将其转换为下标从1开始数的小数点的位置len=d.size();//此时已经把小数点删除,这个长度就是整个数的长度//存入arr数组中 前面已经反转过了 相当于这里就是倒序存入for(int i=0;i<len;i++){arr[i+1]=d[i]-'0';}for(int i=1;i<=n;i++){kkkk();//高精度乘法 每次乘2}//此时已经乘完了所有2 但我们还需要判断一次进位 因为题目说的是输出四舍五入后的整数//这里我们只要判断小数点后第一位数是否大于等于5就可以了if(arr[dex]>=5){arr[dex+1]++;}//进位更新for(int i=dex+1;i<=len;i++){arr[i+1]+=arr[i]/10;arr[i]%=10;}//查看长度是否变化if(arr[len+1]){len++;}//输出整数部分for(int i=len;i>dex;i--){cout<<arr[i];}return 0;
}
五、试题F:数字接龙


1.备注!!!!
这题需要dfs的知识,需要刷过类似于走迷宫的题目,请了解后再看题解,题解不会详细对此知识点进行教程
2.题意分析
这题当时我第一次提交是过了75%,个人感觉这题就是迷宫的简单题 但是关键点就是这个路径不能交叉,然后题意很明确,题目中把每个条件都列出来了,所以就不需要再将复杂题意翻译为简单题意了
3.个人思路解析
首先大致思路就是走迷宫 用dfs 因为结合题意,并且看到地图最大为10*10,我们直接上dfs 并且不需要剪枝,也不需要记忆化搜索,这么小直接暴力就行,第一个条件就是从起点到终点,这个不需要多少,第二个条件我们设置一个值next就行,表示下一个需要搜寻的值,第三个条件我们一开始设置一个初始ans=1,然后到搜满的时候,判断这个ans是否等于地图方块总数的时候就行,第四个条件是最关键的点就是不能交叉,大家仔细想一下,怎么样会导致交叉,是不是只有斜着走的时候呢????,因为路线不能重复走,所以如果上下左右走的话就不可能导致交叉,那么斜着走会导致交叉,所以这个关键点就被我们抓住了
我这里单独开一个xvis四维度的一个数组bool xvis[15][15][15][15];//对于走斜线进行标记 从位置i j到 位置 k l 表示 (i,j) 这个坐标到 (k,l) 这个坐标,这条路线走过,我画个图打个比方

(i,j)到(k,l)这个路线被走过了,大家觉得我还能这样斜着从A到B吗?
显然是不能的,因为已经走过了,但是这里也有一个关键点!! 我们将
xvis[i][j][k][l]变为1的时候,虽然表示的是从(i,k)到(k,l)这条路走过,但是不是也要将xvis[k][l][i][j]变为1,表示从(k,l)到(i,j)这条路走过,大家想一下是不是这个道理????????
题目中还有一个关键点,就是要我们找到这条路径的时候,按字典序输出!
这个其实很简单,因为题目中把每个方向表示的顺序告诉了我们,我们在遍历方向的时候,按从小到大的顺序遍历即可
到此为止我们把所有条件都翻译出来了,下面我们直接上代码!!!!
5.代码解答
#include<iostream>
#include<vector>
using namespace std;
int n,m,mp[15][15],ans=1;//ans表示走过多少格子 当走过格子数==总格子数 说明全部格子都经过了
bool vis[15][15];//标记此路线是否走过
bool xvis[15][15][15][15];//对于走斜线进行标记 从位置i j到 位置 k l
bool flag=0;//查看最终是否找到一条合适的线路
vector<int>path;//存储路线
//按照图例给的顺序进行此顺序的遍历方向
int dx[]={-1,-1,0,1,1,1,0,-1};
int dy[]={0,1,1,1,0,-1,-1,-1};
int p[]={0,1,2,3,4,5,6,7};//每个方向路线代表的数字void dfs(int x,int y,int next)
{if(next==m)next=0;//重置if(x==n-1&&y==n-1)//到达终点 {if(ans==n*n&&!flag)//成功走满所有格子 并且还没有找到一条路线{for(int i=0;i<path.size();i++){cout<<path[i];}flag=1;}return;}//依次搜寻每一条方向for(int i=0;i<8;i++){int xx=x+dx[i];int yy=y+dy[i];if(xx<0||yy<0||xx>=n||yy>=n)continue;//越界if(mp[xx][yy]!=next)continue;//不是正确的格子if(vis[xx][yy])continue;//走过了//只有斜着走会导致相交 这里我们判断一下即可if(i==1)//向右上角走 所以要判断上面和右边的路线是否斜着走过{if(xvis[x][y+1][x-1][y]||xvis[x-1][y][x][y+1])continue;}else if(i==3)//向右下角走 所以要判断右侧和下面这个路径是否走过{if(xvis[x][y+1][x+1][y]||xvis[x+1][y][x][y+1])continue;}else if(i==5)//向左下角走 所以要判断左侧和下面这个路径是否走过{if(xvis[x][y-1][x+1][y]||xvis[x+1][y][x][y-1])continue;}else if(i==7)//向左上角走 所以要判断左侧和上面这个路径是否走过{if(xvis[x-1][y][x][y-1]||xvis[x][y-1][x-1][y])continue;}//全部排除完后 这一步可以走if(i==1||i==3||i==5||i==7)//更新斜线{xvis[x][y][xx][yy]=1;xvis[xx][yy][x][y]=1;}vis[xx][yy]=1;//更新标记path.push_back(p[i]);//压入路径ans++;dfs(xx,yy,next+1);ans--;vis[xx][yy]=0;//重置标记path.pop_back();//重置路径//重置斜线if(i==1||i==3||i==5||i==7)//更新斜线{xvis[x][y][xx][yy]=0;xvis[xx][yy][x][y]=0;}}}int main()
{cin>>n>>m;//输入地图大小和Kfor(int i=0;i<n;i++){for(int j=0;j<n;j++){cin>>mp[i][j];//给地图填数}}vis[0][0]=1;//起点走过dfs(0,0,1);//初始位置 下一个位置要找1 if(!flag){cout<<"-1";}return 0;
}
六、试题H:拔河(原省赛最后一题)
1.备注
虽然这题是省赛最后一题并且在洛谷为绿题,但个人觉得这题比那个宝石组合要简单,可能由于我数学比较差并且正好最近又学了一下双指针优化,所以宝石组合那道题对于我来说比较难,我放到最后讲
2.题目


3.知识点说明
此题需要用到 前缀和+双指针进行优化,请大家先学习后再看此题解,关于双指针我之前发了一篇讲解,请大家可以点击这进行学习双指针(滑动窗口)学习!!!
4.思路分析
首先我们分析题意将题目翻译为人话就是给你一条很长的数组,然后分别选两条连续的子数组,这两条子数组不能重叠,然后让这两个子数组的差最小,大概就是这么个意思
Question1:为什么会想到前缀和?
因为我们发现,如果我们找到了两个数组,那我们需要分别求出两个数组的和,然后进行差运算,既然要求一段数组的和,我们自然就想到了前缀和
Question2:为什么会想到用双指针优化?
前面我们想到了用前缀和来记录前n个数组的长度,我一开始的思路是,用for去遍历,找到第一组队伍的起点和终点,然后用for去遍历,找到第二组队伍的起点和终点,就像这样
for(int i=1;i<n;i++)//找到第一支队伍的起点i
{for(int j=i;j<n;j++)//找到第一支队伍的终点j{for(int k=j+1;k<=n;k++)//找到第二支队伍的起点k{for(int h=k;h<=n;h++)//找到第二支队伍的终点h{}}}
}
但我们此时再看数据,n最大是10的3次方,这里四个for就到达了10的12次方了,还没算其他判断的程序
此时我们就能想到用双指针来优化(本人恰好也只会这个来优化)
我们只用两个for去判断第一个队伍的起点和终点,然后用双指针来判断第二个队伍的起点和终点,使得复杂度大大降低!
关于如何用双指针请看我之前发的,如果你此时有这样的疑惑,说明没学过或者没学懂双指针,请先去学习
下面我们直接上代码!!!
5.代码解答
#include<iostream>
#include<algorithm>
using namespace std;
typedef long long ll;
ll n,arr[1005],pre[1005],minn=1e10;int main()
{cin>>n;for(int i=1;i<=n;i++){cin>>arr[i];pre[i]=pre[i-1]+arr[i];}for(int i=1;i<n;i++)//第一组起点{for(int j=i;j<n;j++)//第一组终点{ll sum1=pre[j]-pre[i-1];int left=j+1;//第二组起点int right=j+1;//第二组终点while(right<=n&&left<=right)//双指针枚举起点和终点{ll sum2=pre[right]-pre[left-1];ll t=abs(sum1-sum2);if(t<minn)minn=t;//更新if(sum2<sum1&&right<n)//拓宽{right++;}else if(sum2>sum1&&left<right){left++;}else {if(right<n){right++;if(left<right)left++;}else{break;}}}}}cout<<minn;return 0;
}
6.注意点
个人感觉双指针最容易错的地方就是在边界的时候怎么去移动,要根据题目去判断,这个点如果写错,特别陷入死循环,我经常出错,还是练少了
七、试题E: 宝石组合
后续更新… . . … . . . . . . . . . … . .
八、试题G: 爬山
此题有争议,这题不讲!!!!!!
总结
祝各位佬统统拿奖!!!!!!!!!
相关文章:

第十五届蓝桥杯----B组cpp----真题解析(小白版本)
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 必看前言!!!!!一、试题A:握手问题1.题意分析2.代码解答 二、试题B:小球反弹1.题意…...

软考架构师笔记-数据库系统
1.7 数据库系统 三级模式-两级映射 三级模式 外模式:用户视图概念模式:只涉及描述内模式:存储方式的描述 两级映射 外模式-概念模式映射概念模式-内模式映射 数据库的设计 步骤 需求分析 输出为需求分析、数据流图(Data FLow Diagram-DF…...
)
Spring AI 1.0.0-M6 快速开始(一)
Spring AI 1.0.0-M6 入门一、存储库二、依赖管理完整maven 入门 Spring 是JAVA中我们经常使用的框架之一,Spring AI不断的发展迭代目前已经到M6版本据说上半年会出一个稳定版本。 本节提供了如何开始使用Spring AI的M6。 一、存储库 1.0 M6 -添加Spring存储库 需…...
go 分布式redis锁的实现方式
go 语言以高并发著称。那么在实际的项目中 经常会用到锁的情况。比如说秒杀抢购等等场景。下面主要介绍 redis 布式锁实现的两种高并发抢购场景。其实 高并发 和 分布式锁 是一个互斥的两个状态: 方式一 setNX: 使用 redis自带的API setNX 来实现。能解决…...

Unity中Stack<T>用法以及删除Stack<GameObject>的方法
Unity中Stack用法以及删除Stack的方法 介绍Stack<T>的APIStack<T> 常用方法创建和初始化 Stack<T>Push 和 Pop 操作Stack<T>遍历清空栈检查栈是否包含某个元素 栈的典型应用场景撤销操作深度优先搜索(DFS)注意事项 总结 介绍 因…...
)
Vue进阶之Vue3源码解析(二)
Vue3源码解析 运行runtime-coresrc/createApp.tssrc/vnode.ts.tssrc/renderer.ts runtime-domsrc/index.ts 总结 运行 runtime-core src/createApp.ts vue的创建入口 import { createVNode } from "./vnode";export function createAppAPI(render) {return funct…...
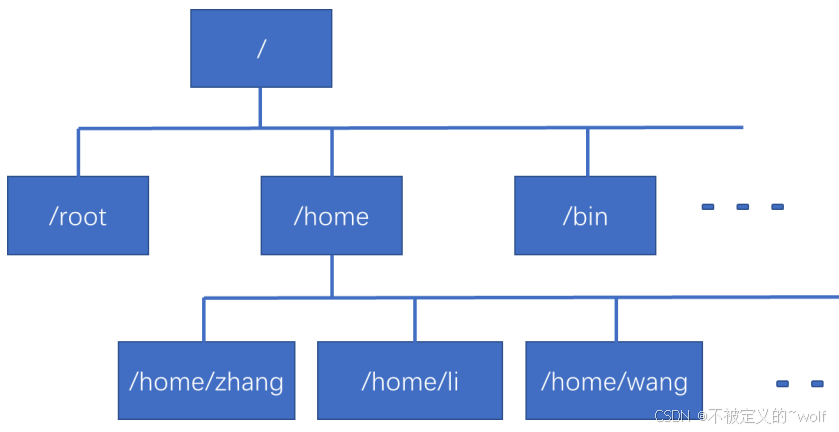
linux的文件系统及文件类型
目录 一、Linux支持的文件系统 二、linux的文件类型 2.1、普通文件 2.2、目录文件 2.3、链接文件 2.4、字符设备文件: 2.5、块设备文件 2.6、套接字文件 2.7、管道文件 三、linux的文件属性 3.1、关于权限部分 四、Linux的文件结构 五、用户主目录 5.1、工作目录…...

如何下载安装 PyCharm?
李升伟 整理 一、下载 PyCharm 访问官网 打开 PyCharm 官网,点击 "Download" 按钮25。 版本选择: 社区版(Community):免费使用,适合个人学习和基础开发。 专业版(Professional&#…...
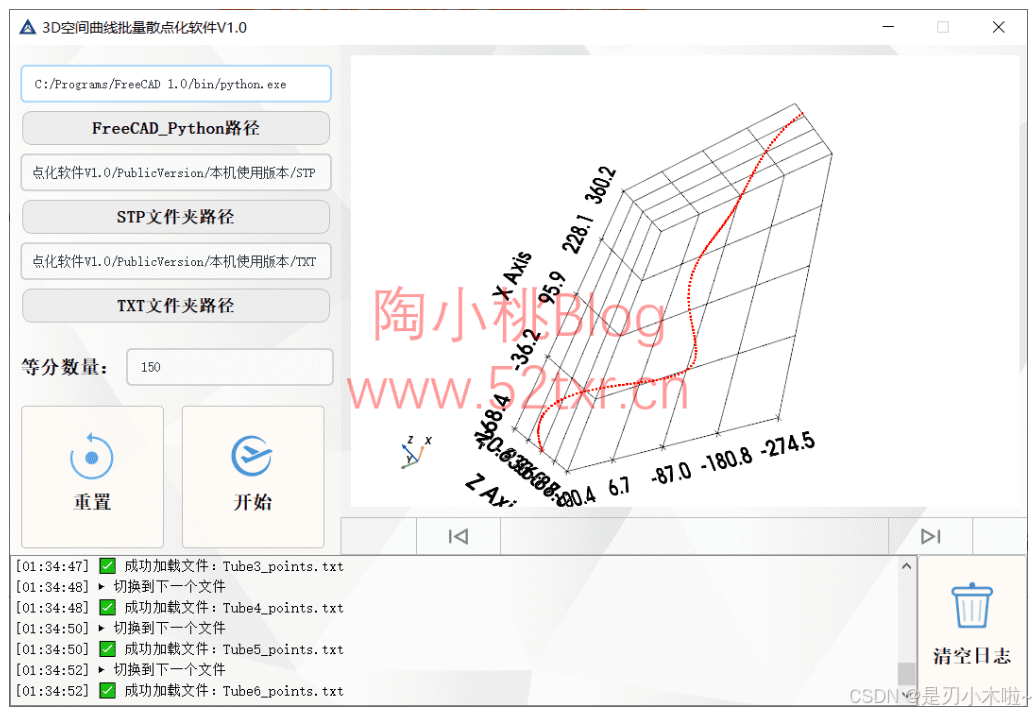
3D空间曲线批量散点化软件V1.0正式发布,将空间线条导出坐标点,SolidWorks/UG/Catia等三维软件通用
软件下载地址: SolidWorks/UG/Catia等三维软件通用,3D空间曲线批量散点化软件V1.0正式发布,将空间线条导出坐标点 - 陶小桃Blog在三维设计领域,工程师常需将复杂空间曲线转化为离散坐标点以用于逆向工程、有限元分析、数控加工或…...
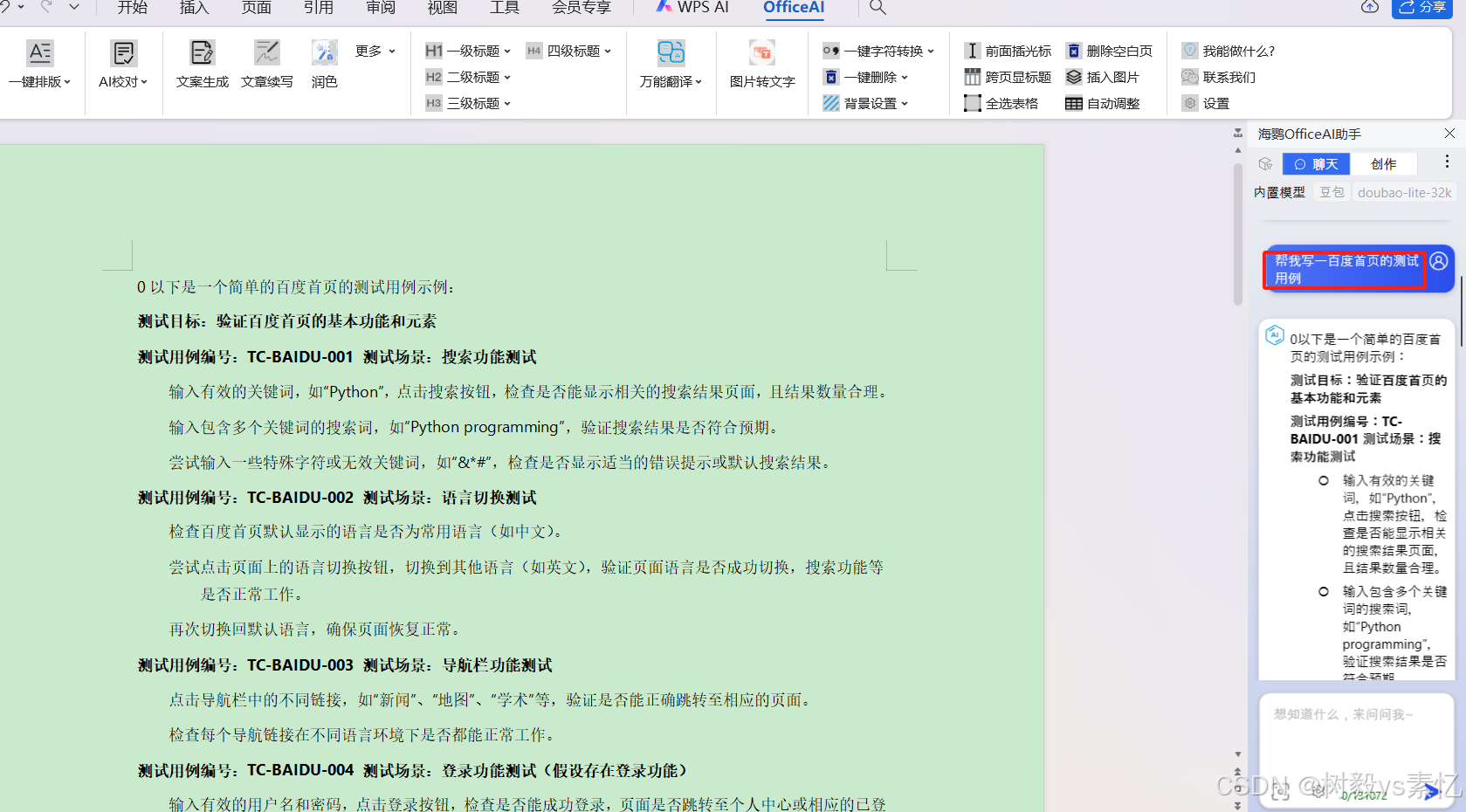
WPS AI+office-ai的安装、使用
** 说明:WPS AI和OfficeAI是两个独立的AI助手,下面分别简单讲下如何使用 ** WPS AI WPS AI是WPS自带AI工具 打开新版WPS,新建文档后就可以看到菜单栏多了一个“WPS AI”菜单,点击该菜单,发现下方出现很多菜单…...

java后端开发day27--常用API(二)正则表达式爬虫
(以下内容全部来自上述课程) 1.正则表达式(regex) 可以校验字符串是否满足一定的规则,并用来校验数据格式的合法性。 1.作用 校验字符串是否满足规则在一段文本中查找满足要求的内容 2.内容定义 ps:一…...

拼电商客户管理系统
内容来自:尚硅谷 难度:easy 目 标 l 模拟实现一个基于文本界面的 《 拼电商客户管理系统 》 l 进一步掌握编程技巧和调试技巧,熟悉面向对象编程 l 主要涉及以下知识点: 类结构的使用:属性、方法及构造器 对象的创建与…...

华为:Wireshark的OSPF抓包分析过程
一、OSPF 的5包7状态 5个数据包 1.Hello:发现、建立邻居(邻接)关系、维持、周期保活;存在全网唯一的RID,使用IP地址表示 2.DBD:本地的数据库的目录(摘要),LSDB的目录&…...

Android项目优化同步速度
最近项目需要使用ffmpeg,需要gradle配置引入ffmpeg库,发现原来通过google官方的代码仓,下载太慢了,每秒KB级别的速度。(之前下gradle/gradle plugin都不至于这么慢),于是想到配置国内镜像源来提…...
在线教育网站项目第二步 :学习roncoo-education,服务器为ubuntu22.04.05
一、说明 前端技术体系:Vue3 Nuxt3 Vite5 Vue-Router Element-Plus Pinia Axios 后端技术体系:Spring Cloud Alibaba2021 MySQL8 Nacos Seata Mybatis Druid redis 后端系统:roncoo-education(核心框架:S…...
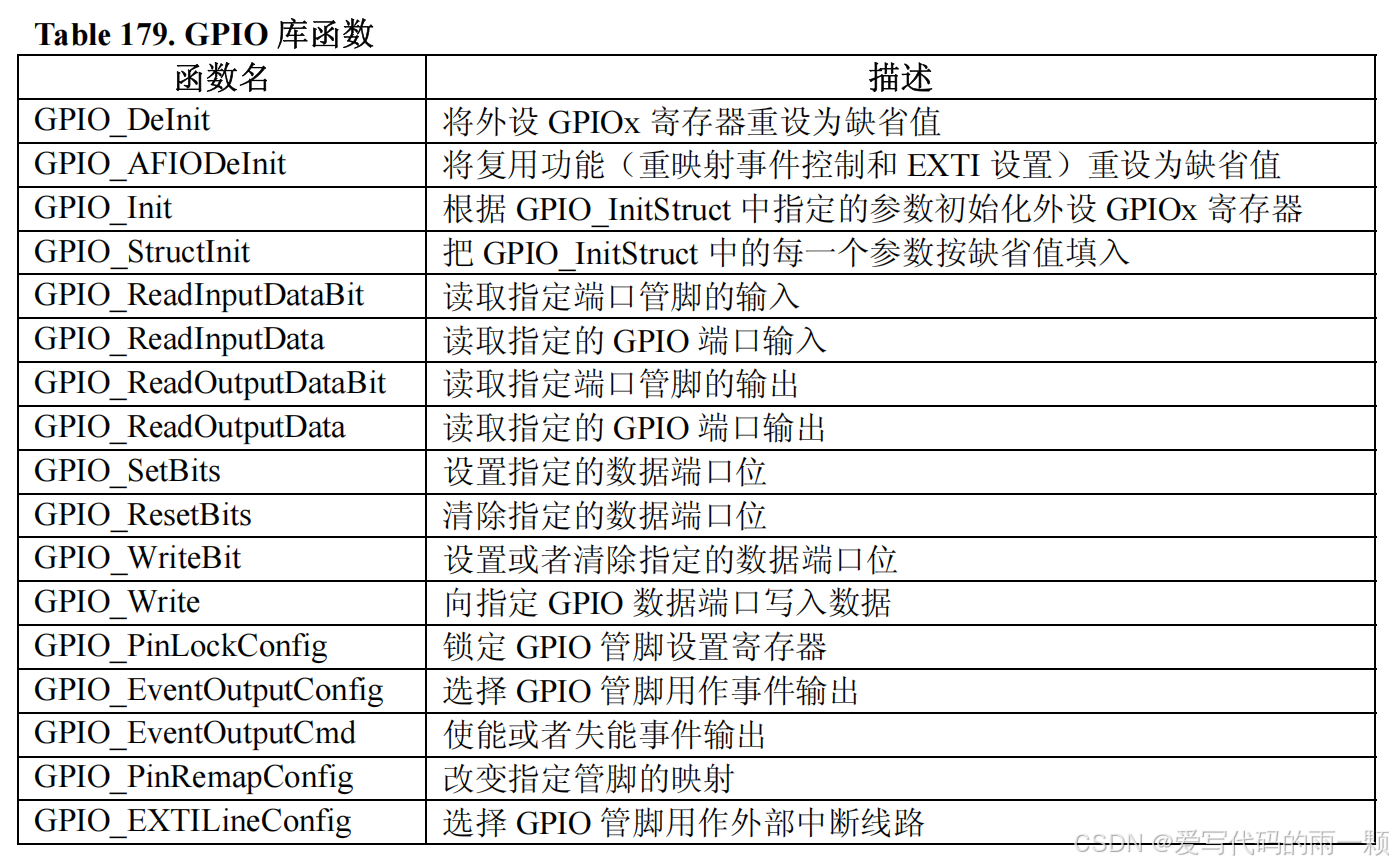
STM32-GPIO详解
目录 一:GPIO基本概念 编辑 二:GPIO的实际应用 三:功能描述 四:GPIO库函数 五:寄存器 GPIO相关寄存器功能 一:GPIO基本概念 GPIO是英文General Purpose Input/Output的缩写,中文翻译为…...

【Framework系列之Client】UIManager和UIPanel模块介绍
今天来介绍一下UIManager和UIPanel模块,话不多说直接开始。 UIManager 功能介绍 UIManager是管理UIPanel的唯一模块,UIManager的主要功能包括: 提供打开、隐藏、关闭UIPanel的相关接口。负责UIPanel对象的创建以及初始化。负责储存UIPanel对…...
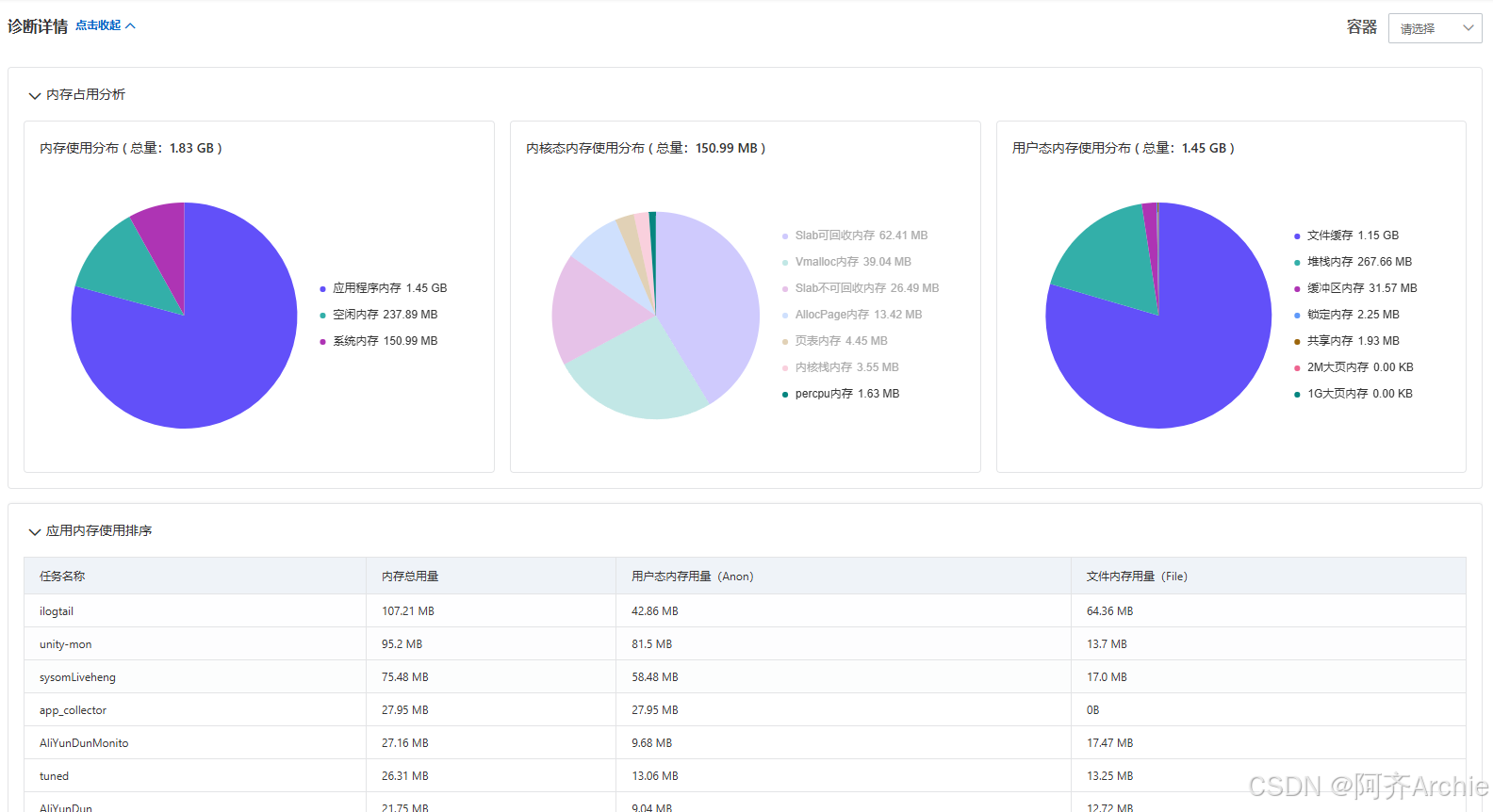
阿里云操作系统控制台——ECS操作与性能优化
引言:在数字化时代,云服务器作为强大的计算资源承载平台,为企业和开发者提供了灵活且高效的服务。本文将详细介绍如何一步步操作云服务器 ECS,从开通到组件安装,再到内存全景诊断,帮助快速上手,…...
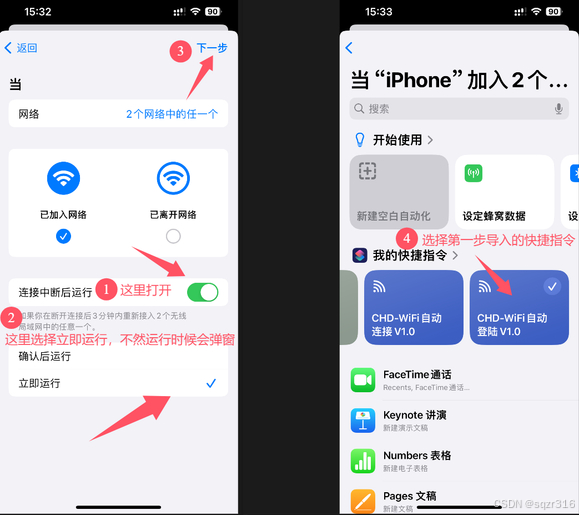
【长安大学】苹果手机/平板自动连接认证CHD-WIFI脚本(快捷指令)
背景: 已经用这个脚本的记得设置Wifi时候,关闭“自动登录” 前几天实在忍受不了CHD-WIFI动不动就断开,一天要重新连接,点登陆好几次。试了下在网上搜有没有CHD-WIFI的自动连接WIFI自动认证脚本,那样我就可以解放双手&…...
第51天:Web开发-JavaEE应用SpringBoot栈身份验证JWT令牌Security鉴权安全绕过
#知识点 1、安全开发-JavaEE-身份验证-JWT&Security 2、安全开发-JavaEE-安全问题-不安全写法&版本漏洞 #开发框架-SpringBoot 参考:Spring Boot 中文文档 一、身份验证的常见技术: 1、JWT 2、Shiro 3、Spring Security 4、OAuth 2.0 5、SSO 6、…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...

c++第七天 继承与派生2
这一篇文章主要内容是 派生类构造函数与析构函数 在派生类中重写基类成员 以及多继承 第一部分:派生类构造函数与析构函数 当创建一个派生类对象时,基类成员是如何初始化的? 1.当派生类对象创建的时候,基类成员的初始化顺序 …...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...

在 Spring Boot 中使用 JSP
jsp? 好多年没用了。重新整一下 还费了点时间,记录一下。 项目结构: pom: <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://ww…...
