c++实现最大公因数和最小公倍数
最大公因数和最小公倍数的介绍
读这篇文章,请你先对最大公因数以及最小公倍数进行了解:
最大公因数(英文名:gcd)
- 定义:最大公因数,也称最大公约数,指两个或多个整数共有约数(因数)中最大的一个。

- 求法
- 列举法:分别列出两个数的所有约数,然后找出它们共有的约数中最大的那个。

- 分解质因数法:

- 辗转相除法:用较大数除以较小数得到商和余数,再用除数和余数反复做除法运算,当余数为 0 时,取当前算式除数为最大公因数。

- 列举法:分别列出两个数的所有约数,然后找出它们共有的约数中最大的那个。
-
最小公倍数(英文名:lcm)
- 几个数共有的倍数叫做这几个数的公倍数,其中除 0 以外最小的一个公倍数,叫做这几个数的最小公倍数。例如,4 的倍数有 4、8、12、16、20、24……,6 的倍数有 6、12、18、24、30……,4 和 6 的公倍数有 12、24……,其中最小的是 12,所以 4 和 6 的最小公倍数是 12,可记作[4,6]:12。
- 求法
- 列举法:分别列出两个数的倍数,然后找出它们共有的倍数中最小的那个。如求 3 和 5 的最小公倍数,3 的倍数有 3、6、9、12、15、18……,5 的倍数有 5、10、15、20……,它们的最小公倍数是 15。
- 分解质因数法:把它们公有的质因数与每个数独有的质因数连乘起来,所得的积就是它们的最小公倍数。例如,12=2×2×3,15=3×5,所以

- 公式法:对于两个数a和b,[a,b]=a*b/(a,b)。例如:

代码:
#include <bits/stdc++.h>
using namespace std;
long long x=0,y=0;
long long pri[100000],cnt=0;
long long gcd(long long a,long long b) {return !b?a:gcd(b,a%b);
}
void gprime(long long num) {cout<<num<<"=";long long divisor=2;bool first=true;while(num>1) {if(num%divisor==0) {if(!first) {cout<<"*";}cout<<divisor;num/=divisor;first=false;} else {divisor++;}}cout<<endl;
}
vector<long long>commonFactors(long long a,long long b) {vector<long long>factors;for(long long i=1; i<=min(a,b); i++) {if(a%i==0&&b%i==0) {factors.push_back(i);}}return factors;
}
long long poww(long long x) {long long f1=x,cnt=0;while(f1) {f1/=10;cnt++;}return cnt;
}
bool Is_Prime(long long x) {for(long long i=2; i<x; i++) {if(x%i==0) {return 0;}}return 1;
}
void Print(long long a,long long b) {cout<<"分解质因数过程:"<<endl;gprime(a);gprime(b);vector<long long>factors=commonFactors(a,b);cout<<a<<"和"<<b<<"的公因数有:";for(long long factor:factors) {cout<<factor<<" ";}cout<<"\n";if(gcd(a,b)==1) {cout<<"互质,没有过程。\n";} else {cout<<"输出短除法过程\n";long long k=poww(a)+poww(b)+5,back;long long fa=a,fb=b;while(gcd(fa,fb)!=1) {for(long long i=2;; i++) {if(Is_Prime(i)&&fa%i==0&&fb%i==0) {cnt++;pri[cnt]=i;cout<<i<<" | "<<fa<<" "<<fb<<"\n";for(long long j=1; j<=poww(i)+1; j++) {cout<<" ";}for(long long j=1; j<=k; j++) {cout<<"-";}fa/=i;fb/=i;cout<<"\n";if(gcd(fa,fb)==1) {back=i;x=fa;y=fb;}break;}}}for(long long i=1; i<=poww(back)+3; i++) {cout<<" ";}cout<<fa<<" "<<fb<<"\n";}if(gcd(a,b)==1) {cout<<"("<<a<<","<<b<<"):"<<gcd(a,b)<<"\n";cout<<"["<<a<<","<<b<<"]:";if(gcd(a,b)==1) {cout<<a<<"*"<<b<<"\n";for(long long i=1; i<=poww(a)+poww(b)+3; i++) {cout<<" ";}cout<<"=";}cout<<a*b/gcd(a,b);return ;}cout<<"("<<a<<","<<b<<"):";long long anss=1;for(long long i=1; i<=cnt; i++) {anss*=pri[i];cout<<pri[i];if(i!=cnt) {cout<<"*";}}cout<<"\n";for(long long i=1; i<=poww(a)+poww(b)+3; i++) {cout<<" ";}cout<<"="<<anss;cout<<"\n["<<a<<","<<b<<"]:";for(long long i=1; i<=cnt; i++) {cout<<pri[i]<<"*";}cout<<x<<"*"<<y<<"\n";for(long long i=1; i<=poww(a)+poww(b)+3; i++) {cout<<" ";}cout<<"="<<anss<<"*"<<x*y<<"\n";for(long long i=1; i<=poww(a)+poww(b)+3; i++) {cout<<" ";}cout<<"="<<gcd(a,b)<<"\n";cout<<"("<<a<<","<<b<<"):"<<gcd(a,b)<<"\n";cout<<"["<<a<<","<<b<<"]:";if(gcd(a,b)==1) {cout<<a<<"*"<<b<<"\n";for(long long i=1; i<=poww(a)+poww(b)+3; i++) {cout<<" ";}cout<<"=";}cout<<a*b/gcd(a,b);
}
int main() {cout<<"输入两个整数:\n";cout<<"本程序用于计算两个数的gcd(最大公因数、最大公约数)以及lcm,其中,(a,b)表示两个数的gcd,[a,b]表示两个数的lcm\n";long long a,b;cin>>a>>b;system("cls");if(gcd(a,b)==1) {cout<<"检测到互质,将自动省略过程\n";Print(a,b);return 0;}if(gcd(a,b)==min(a,b)){cout<<"检测到有倍数关系,这里推荐使用不要过程,请慎重选择\n";}cout<<"输入模式:\n";cout<<"0.只要答案\n";cout<<"其他任何数.要过程\n";long long sr;if(!sr&&gcd(a,b)==min(a,b)){cout<<"("<<a<<","<<b<<"):"<<min(a,b)<<"\n";cout<<"["<<a<<","<<b<<"]:"<<max(a,b)<<"\n";return 0;}cin>>sr;system("cls");if(!sr) {cout<<"("<<a<<","<<b<<"):"<<gcd(a,b)<<"\n";cout<<"["<<a<<","<<b<<"]:";if(gcd(a,b)==1) {cout<<a<<"*"<<b<<"\n";for(long long i=1; i<=poww(a)+poww(b)+3; i++) {cout<<" ";}cout<<"=";}cout<<a*b/gcd(a,b);return 0;}Print(a,b);return 0;
}相关文章:

c++实现最大公因数和最小公倍数
最大公因数和最小公倍数的介绍 读这篇文章,请你先对最大公因数以及最小公倍数进行了解: 最大公因数(英文名:gcd) 定义:最大公因数,也称最大公约数,指两个或多个整数共有约数&…...

知识库Dify和cherry无法解析影印pdf word解决方案
近期收到大量读者反馈:上传pdf/图文PDF到Dify、Cherry Studio等知识库时,普遍存在格式错乱、图片丢失、表格失效三大痛点。 在试用的几款知识库中除了ragflow具备图片解析的能力外,其他的都只能解析文本。 如果想要解析扫描件,…...

【记录一下学习】Embedding 与向量数据库
一、向量数据库 向量数据库(Vector Database),也叫矢量数据库,主要用来存储和处理向量数据。 在数学中,向量是有大小和方向的量,可以使用带箭头的线段表示,箭头指向即为向量的方向,…...

【第21节】C++设计模式(行为模式)-Chain of Responsibility(责任链)模式
一、问题背景 在 VC/MFC 开发中,消息处理机制是核心部分之一。VC 是基于消息和事件驱动的框架,消息的处理流程通常是通过链式传递的方式进行的。例如,一个 WM_COMMAND 消息的处理流程可能如下: (1)MDI 主窗…...

createrepo centos通过nginx搭建本地源
yum update 先安装一个nginx。 安装Nginx yum install gcc gcc-c pcre pcre-devel openssl openssl-devel libtool zlib zlib-devel -y cd /usr/local/src wget http://nginx.org/download/nginx-1.22.0.tar.gz tar -zxvf nginx-1.22.0.tar.gz cd nginx-1.22.0 ./configu…...

在 Docker 中搭建GBase 8s主备集群环境
本文介绍了如何在同一台机器上使用 Docker 容器搭建GBase 8s主备集群环境。 拉取镜像 拉取GBase 8s的最新镜像 docker pull liaosnet/gbase8s或者docker pull liaosnet/gbase8s:v8.8_3513x25_csdk_x64注:在tag为v8.8_3513x25_csdk_x64及之后的版本中,…...

【MySQL-数据类型】数据类型分类+数值类型+文本、二进制类型+String类型
一、数据类型分类 二、数值类型 1.bit类型 测试环境ubuntu 基本语法: bit[(M)]:位字段类型,M表示每个值的位数,范围从1~64;如果M被忽略,默认为1举例: create table testBit(id i…...

小谈java内存马
基础知识 (代码功底不好,就找ai优化了一下) Java内存马是一种利用Java虚拟机(JVM)动态特性(如类加载机制、反射技术等)在内存中注入恶意代码的攻击手段。它不需要在磁盘上写入文件,…...

简单的二元语言模型bigram实现
内容总结归纳自视频:【珍藏】从头开始用代码构建GPT - 大神Andrej Karpathy 的“神经网络从Zero到Hero 系列”之七_哔哩哔哩_bilibili 项目:https://github.com/karpathy/ng-video-lecture Bigram模型是基于当前Token预测下一个Token的模型。例如&#x…...

【清华大学】实用DeepSeek赋能家庭教育 56页PDF文档完整版
清华大学-56页:实用DeepSeek赋能家庭教育.pdf https://pan.baidu.com/s/1BUweVDeG2M8-t0QaIs3LHQ?pwd1234 提取码: 1234 或 https://pan.quark.cn/s/8a9473493bb0 《实用DeepSeek赋能家庭教育》基于清华大学研究成果,系统阐述了DeepSeek人工智能技…...
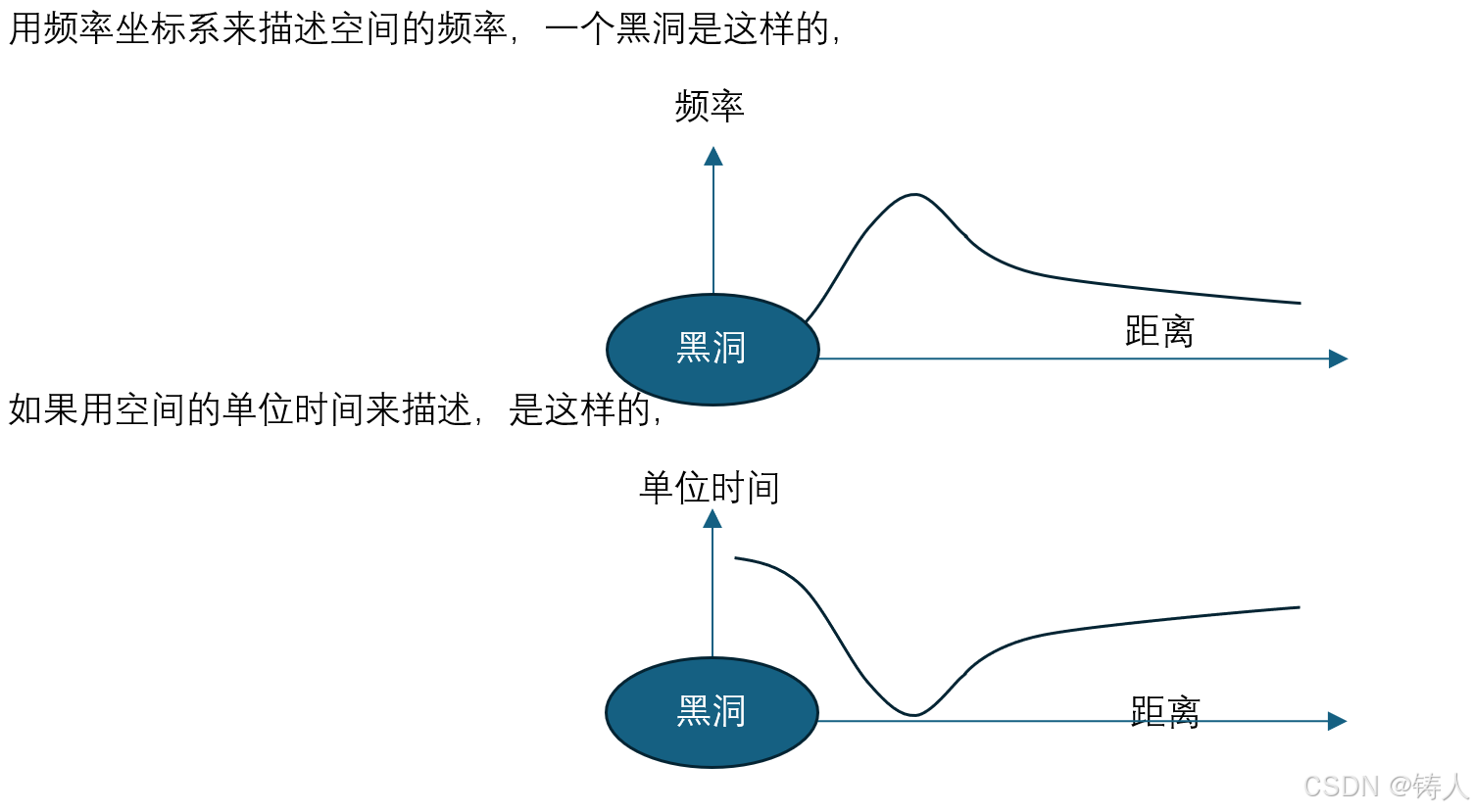
黑洞如何阻止光子逃逸
虽然涉及广义相对论,但广义相对论说的是大质量物体对周围空间的影响,而不是说周围空间和空间中的光子之间的关系。也就是说,若讨论光子逃逸问题,则不必限定于大质量的前提,也就是说,若质量周围被扭曲的空间…...

1.4 单元测试与热部署
本次实战实现Spring Boot的单元测试与热部署功能。单元测试方面,通过JUnit和Mockito等工具,结合SpringBootTest注解,可以模拟真实环境对应用组件进行独立测试,验证逻辑正确性,提升代码质量。具体演示了HelloWorld01和H…...

window系统中的start命令详解
start 是 Windows 系统中用于启动新进程或打开新窗口来运行指定程序或命令的命令。以下是对 start 命令参数的详细解释: 基本语法 start ["title"] [/Dpath] [/I] [/MIN] [/MAX] [/SEPARATE | /SHARED] [/LOW | /NORMAL | /HIGH | /REALTIME | /ABOVENO…...

AI编程工具节选
1、文心快码 百度基于文心大模型推出的一款智能编码助手, 官网地址:文心快码(Baidu Comate)更懂你的智能代码助手 2、通义灵码 阿里云出品的一款基于通义大模型的智能编码辅助工具, 官网地址:通义灵码_你的智能编码助手-阿里云 …...

正则表达式,idea,插件anyrule
package lx;import java.util.regex.Pattern;public class lxx {public static void main(String[] args) {//正则表达式//写一个电话号码的正则表达式String regex "1[3-9]\\d{9}";//第一个数字是1,第二个数字是3-9,后面跟着9个数字…...

原生iOS集成react-native (react-native 0.65+)
由于官方文档比较老,很多配置都不能用,集成的时候遇到很多坑,简单的整理一下 时间节点:2021年9月1日 本文主要提供一些配置信息以及错误信息解决方案,具体步骤可以参照官方文档 原版文档:https://reactnative.dev/docs…...

java错题总结
本篇文章用来记录学习javaSE以来的错题 解答:重载要求俩个方法的名字相同,但参数的类型或者个数不同,但是不要求返回类型相同,所以A正确。 重写还需要要求返回类型相同(呈现父子类关系也可以,但是属于特例&…...
】解锁商品信息录入与展示的技术密码)
【商城实战(10)】解锁商品信息录入与展示的技术密码
【商城实战】专栏重磅来袭!这是一份专为开发者与电商从业者打造的超详细指南。从项目基础搭建,运用 uniapp、Element Plus、SpringBoot 搭建商城框架,到用户、商品、订单等核心模块开发,再到性能优化、安全加固、多端适配…...

2025年主流原型工具测评:墨刀、Axure、Figma、Sketch
2025年主流原型工具测评:墨刀、Axure、Figma、Sketch 要说2025年国内产品经理使用的主流原型设计工具,当然是墨刀、Axure、Figma和Sketch了,但是很多刚入行的产品经理不了解自己适合哪些工具,本文将从核心优势、局限短板、协作能…...

MDM 如何彻底改变医疗设备的远程管理
在现代医疗行业迅速发展的格局中,医院和诊所越来越依赖诸如医疗平板和移动工作站等移动设备。这些设备在提高工作效率和提供卓越的患者护理方面发挥着关键作用。然而,随着它们的广泛使用,也带来了一系列挑战,例如在不同地点确保数…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...

Linux中《基础IO》详细介绍
目录 理解"文件"狭义理解广义理解文件操作的归类认知系统角度文件类别 回顾C文件接口打开文件写文件读文件稍作修改,实现简单cat命令 输出信息到显示器,你有哪些方法stdin & stdout & stderr打开文件的方式 系统⽂件I/O⼀种传递标志位…...

OCR MLLM Evaluation
为什么需要评测体系?——背景与矛盾 能干的事: 看清楚发票、身份证上的字(准确率>90%),速度飞快(眨眼间完成)。干不了的事: 碰到复杂表格(合并单元…...

ThreadLocal 源码
ThreadLocal 源码 此类提供线程局部变量。这些变量不同于它们的普通对应物,因为每个访问一个线程局部变量的线程(通过其 get 或 set 方法)都有自己独立初始化的变量副本。ThreadLocal 实例通常是类中的私有静态字段,这些类希望将…...

从实验室到产业:IndexTTS 在六大核心场景的落地实践
一、内容创作:重构数字内容生产范式 在短视频创作领域,IndexTTS 的语音克隆技术彻底改变了配音流程。B 站 UP 主通过 5 秒参考音频即可克隆出郭老师音色,生成的 “各位吴彦祖们大家好” 语音相似度达 97%,单条视频播放量突破百万…...

32位寻址与64位寻址
32位寻址与64位寻址 32位寻址是什么? 32位寻址是指计算机的CPU、内存或总线系统使用32位二进制数来标识和访问内存中的存储单元(地址),其核心含义与能力如下: 1. 核心定义 地址位宽:CPU或内存控制器用32位…...
