蓝桥备赛(16)- 树
一、树的概念
1.1 树的定义
1)树型结构(一对多)是⼀类重要的非线性数据结构
2 )有⼀个特殊的结点,称为根结点,根结点没有前驱结点
3)除了根节点外 , 其余结点被分成 M(M > 0) 个互不相交的集合 T1 , T2.....Tm , 其中每个集合 Ti ( 1 <= i <= m) 又是一棵结构与树类似的子树 。 每棵子树的根节点有且只有一个前驱 , 可以有 0 个 或者多个后继 。 因此 , 树是递归定义的。
1.2 树的基本术语
- 结点的度 : 一个结点有几个孩子 --> 度就有多少
- 树的度 : 一棵树中 , 最大的结点的度称为树的度
- 父结点 / 双亲结点 : 若一个结点含有子节点 , 则这个结点称为其子节点的父结点
- 子节点 / 孩子结点 : 一个结点含有的子树的根结点称为该结点的子节点
- 叶子结点 / 终端结点 : 度为 0 的结点称为叶节点
- 分支结点 / 非终端结点: 度不为0的结点
- 兄弟结点 : 具有相同父结点 相互成为兄弟结点 ( 亲兄弟 )
- 结点的层次 : 从根开始定义起 , 根为 第一层 , 根的子结点为第二层 ,依次类推
- 树的高度 或 深度 : 树中结点的最大层次
- 路径 : 一条从树中任意结点出发 , 沿父结点 --> 子结点 连接 ,达到任意结点 的序列
树的概念与结构-CSDN博客

1.3 有序树和无序树
1)有序树:结点的子树按照从左往右的顺序排列,不能更改。2)无序树:结点的子树之间没有顺序,随意更改。这个认知会在我们后续学习二叉树的时候用到,因为二叉树需要区分左右孩子在算法竞赛中 , 遇到的基本上都是无序树 , 也就是说 , 不需要考虑孩子结点的顺序

在有序树的视角中 , 上面两棵树 不相同 ;
但是在无序树的视角中 , 上面两棵树是相同的 。
1.4 有根树和无根树
1)有根树: 树的根节点已知,是固定的。2)无根树:树的根节点未知,谁都可以是根结点
在有根树的视角中 , 根结点为 : A
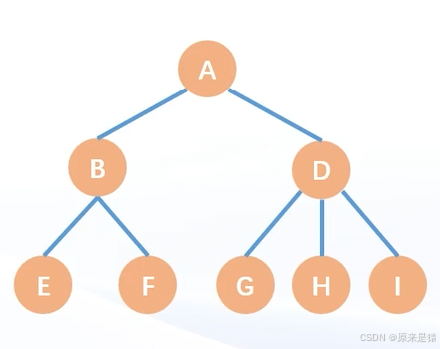
在无根树的视角中 :
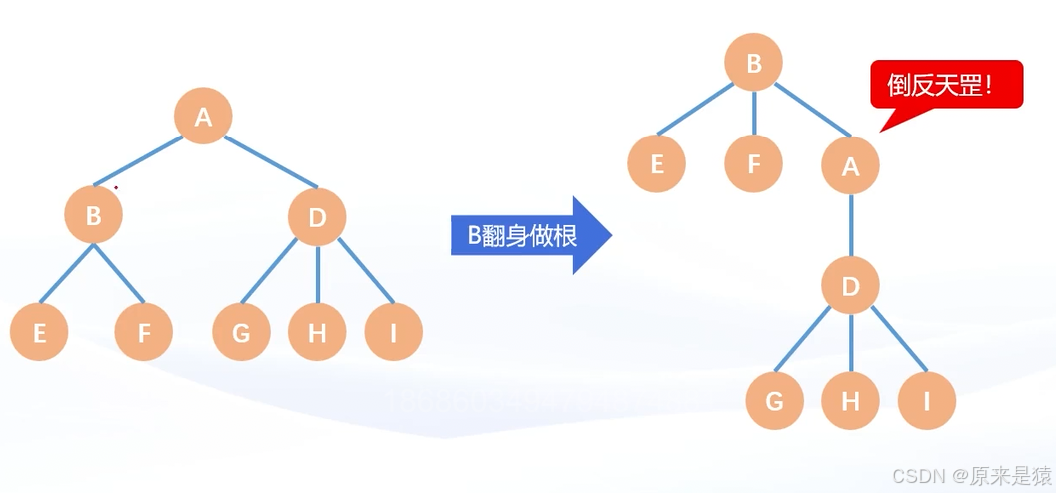
无根树会导致父子关系不明确 , 在存储时候需要注意 。 在算法竞赛中 , 一般遇到的树一般都是无根树 , 即使有根树 , 也会存在父子关系未知的情况 。
二、树的存储
1)树结构相对线性结构来说就比较复杂 。存储时,既要保存值域,也要保存结点与结点之间的关系。2)实际中树有很多种存储方式:双亲表示法,孩子表示法、孩子双亲表示法以及孩子兄弟表示法等。
2.1 孩子表示法
1) 对于每一个结点,只存储所有孩子的信息。
注意:如果在无根树之中 , 如何知道谁是孩子 ? 谁是父亲呢?
----> 管他三七二十一 !!!直接把相连的结点都存储起来!!! 都给我存!起!来!

2.2 实现方式一:用vector数组实现
在算法中 , 一般会给出树结构都是有编号的 , 以简化我们的操作
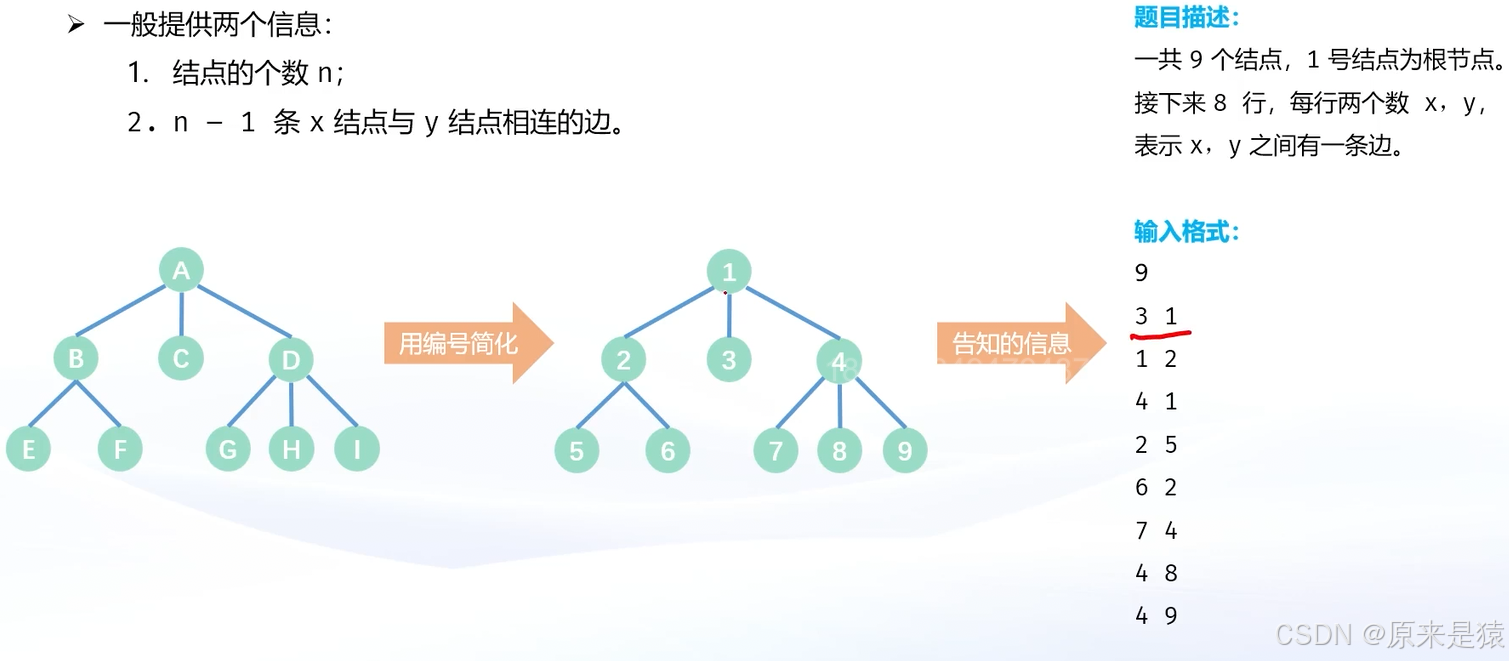
上面的题目,虽然告知了根结点是 1 , 但是其他的结点之间的关系还是未知的 , 所以我们还是需要当成无序树来处理 。
1) 创建一个大小足够的 vector 数组 :vector<int> edges[10];
2) 对于 i 的孩子 , 直接 edges[i] .push_back 进去即可 。


#include <iostream>
#include <cstdio>
#include <vector>
using namespace std;const int N = 1e5 + 10;
int n;
vector<int> edges[N];int main()
{cin >> n;for(int i = 1;i <n ;i ++){int a,b;cin >> a >> b;edges[a].push_back(b);edges[b].push_back(a); }return 0;
}2.3 实现方式二:链式前向星
本质上就是用 链表存储 所有孩子 , 其中链表是用数组模拟实现的 。
#include <iostream>
#include <cstdio>
#include <vector>
using namespace std;const int N = 1e5 + 10;
int h[N],e[N*2],ne[N*2],id;int n;
//其实就是把 b 头插到 a 的链表后面
void add(int a,int b)
{id++;e[id] = b;ne[id] = h[a];h[a] = id;
}
int main()
{cin >> n;for(int i = 1;i <n;i++){int a,b;cin >> a >> b;add(a,b);add(b,a);}return 0;
}2.4 总结
1)前者由于用到了容器 vector,实际运行起来相比较于后者更耗时,因为 vector 是动态实现的。2)但是在如今的算法竞赛中,⼀般不会无聊到卡这种常数时间。也就是 vector 虽然慢,但不会因此而超时。
三、树的遍历
树的遍历就是不重不漏的将树中所有的点都扫描一遍在之前学过的线性结构中,遍历就很容易,直接从前往后扫描⼀遍即可。但是在树形结构中, 如果不按照⼀定的规则遍历,就会漏掉或者重复遍历⼀些结点 。因此,在树形结构中,要按照⼀定规则去遍历。常用的遍历方式有两种,一种是深度优先遍历,另一种是宽度优先遍历。注意 !!!树的遍历是许多关于树的算法的知识 , 一定要掌握啊!!!
3.1 深度优先遍历 -DFS
1)深度优先遍历(DFS -- Depth First Search) , 是一种用于遍历 或 搜索树或图的算法 。
2)每次尝试向更深的结点走 --> 一条路走到黑 !!!走到不能再走的时候 , 返回 , 继续走其他的路。
不撞南墙不回头!!!

因此 , DFS 其实就是利用 递归的形式遍历 , 可以用递归来实现 !
3.1.1 用vector 数组存储
#include <iostream>
#include <cstdio>
#include <vector>
using namespace std;const int N = 1e5 + 10;
int n;
vector<int> edges[N];//存储图
bool st[N];//标记哪些点已经访问了
//方法一:vector 实现 void dfs(int u)
{cout << u << " ";st[u] = true;//说明当前这个点已经访问过了//访问所有的孩子 for(auto v:edges[u]){if(!st[v]){dfs(v);}}
}
int main()
{//建树cin >> n;for(int i = 1; i< n;i++){int a,b;cin >> a >> b;edges[a].push_back(b);edges[b].push_back(a); } //深度优先遍历dfs(1); return 0;
}
3.1.2 链式向前星存储
#include <iostream>
#include <cstdio>
#include <vector>
using namespace std;const int N = 1e5 +10;
int id,h[N],e[N*2],ne[N*2];
int n;
bool st[N];//标记哪些点已经访问过了void add(int a,int b)
{id++;e[id] = b;ne[id] = h[a];h[a] = id;
}void dfs(int u)
{cout << u << " ";st[u] = true;for(int i = h[u];i; i = ne[i]){int v = e[i]; // 孩子if(!st[v])dfs(v); }
}
int main()
{//建树 cin >> n;for(int i = 1;i<n ; i++){int a,b;cin >> a >> b;add(a,b);add(b,a);}//深度优先遍历dfs(1); return 0;
}
与使用vectoc 存储的打印结果不同 , 因为vector 是尾插到数的后面 , 但是链式前向星是头插。
时间复杂度 :简单估计⼀下,在 dfs 的整个过程中,会把树中所有的边扫描量两遍。边的数量为 n − 1 , 因此时间复杂度为 O(N) 。空间复杂度:最差情况下,结点个数为 n 的树,⾼度也是 n ,也就是变成⼀个链表。此时递归的深度也是 n , 此时的空间复杂度为 O(N) 。
3.2 宽度优先遍历 - BFS
宽度优先遍历( BFS --- Breadth First Search),也叫广度优先遍历。也是⼀种用于遍 或搜索树或图的算法。 所谓宽度优先。就是每次都尝试访问同⼀层的节点。 如果同⼀层都访问完了,再访问下一层。一层一层来

3.1.1 用vector 数组存储
#include <iostream>
#include <cstdio>
#include <vector>
#include <queue>
using namespace std;const int N = 1e5 + 10;
bool st[N]; //标记哪一个点已经入队了
int n;
vector<int> edges[N]; void bfs()
{queue<int> q;q.push(1);st[1] = true;while(q.size()){int u = q.front() ;q.pop() ;cout << u << " ";for(auto v : edges[u]){if(!st[v]) {q.push(v);st[v] = true;}} }
}
int main()
{//建树 cin >> n;for(int i = 1 ;i< n ; i++){int a, b;cin >> a >> b;edges[a].push_back(b);edges[b].push_back(a); }//宽度优先遍历bfs(); return 0;
}
3.1.2 链式向前星存储
#include <iostream>
#include <cstdio>
#include <vector>
#include <queue>
using namespace std;const int N = 1e5 +10;
bool st[N];
int id,e[N*2],ne[N*2],h[N];
int n;void add(int a,int b)
{id++;e[id] = b;ne[id] = h[a];h[a] = id;
}
void bfs()
{queue<int> q;q.push(1);st[1] = true;while(q.size() ){int u = q.front() ;q.pop() ;cout << u << " ";for(int i = h[u]; i ; i = ne[i]){int v = e[i];if(!st[v]){q.push(v);st[v] = true; }}}
}
int main()
{cin >> n;//建树for(int i = 1;i<n;i++){int a,b;cin >> a >> b;add(a,b);add(b,a);} bfs();return 0;
}

时间复杂度: 所有结点只会入队一次,然后出队一次,因此时间复杂度为 O(N)空间复杂度: 最坏情况下,所有的非根结点都在同⼀层,此时队列里面最多有 n-1 个元素,空间复杂度为 O(N)
相关文章:

蓝桥备赛(16)- 树
一、树的概念 1.1 树的定义 1)树型结构(一对多)是⼀类重要的非线性数据结构 2 )有⼀个特殊的结点,称为根结点,根结点没有前驱结点 3)除了根节点外 , 其余结点被分成 M(M…...

黑马测试mysql基础学习
视频来源:软件测试工程师所需的MySQL数据库技术,mysql系统精讲课后练习_哔哩哔哩_bilibili 环境准备: 虚拟机Linux服务器安装mysql数据库。本机安装Navicat。使Navicat连接虚拟机的数据库。(麻烦一点的是Navicat连接虚拟机的数据…...

ROS2-话题学习
强烈推荐教程: 《ROS 2机器人开发从入门到实践》3.2.2订阅小说并合成语音_哔哩哔哩_bilibili 构建功能包 # create package demo_python_pkg ros2 pkg create --build-type ament_python --license Apache-2.0 demo_python_pkg 自己写的代码放在./demo_python_pkg/…...

C++指针的基本认识
1.数组做函数参数 首先,所有传递给函数的参数都是通过传值方式进行的,传递给函数的都是参数的一份拷贝。 接着,当传递的参数是一个指向某个变量的指针时,函数将对该指针执行间接访问操作(拷贝指针,并访问所指向的内容),则函数就可以修改指向的变量。 2.一维数组 数组名…...

TypeScript系列06-模块系统与命名空间
1. ES 模块与 CommonJS 互操作性 1.1 模块解析策略 TypeScript 提供多种模块解析策略,每种策略针对不同的运行环境和开发场景优化: // tsconfig.json {"compilerOptions": {"moduleResolution": "node16", // 或 "…...
命令详解:zip)
Linux(Centos 7.6)命令详解:zip
1.命令作用 打包和压缩(存档)文件(package and compress (archive) files);该程序用于打包一组文件进行分发;存档文件;通过临时压缩未使用的文件或目录来节省磁盘空间;且压缩文件可以在Linux、Windows 和 macOS中轻松提取。 2.命…...
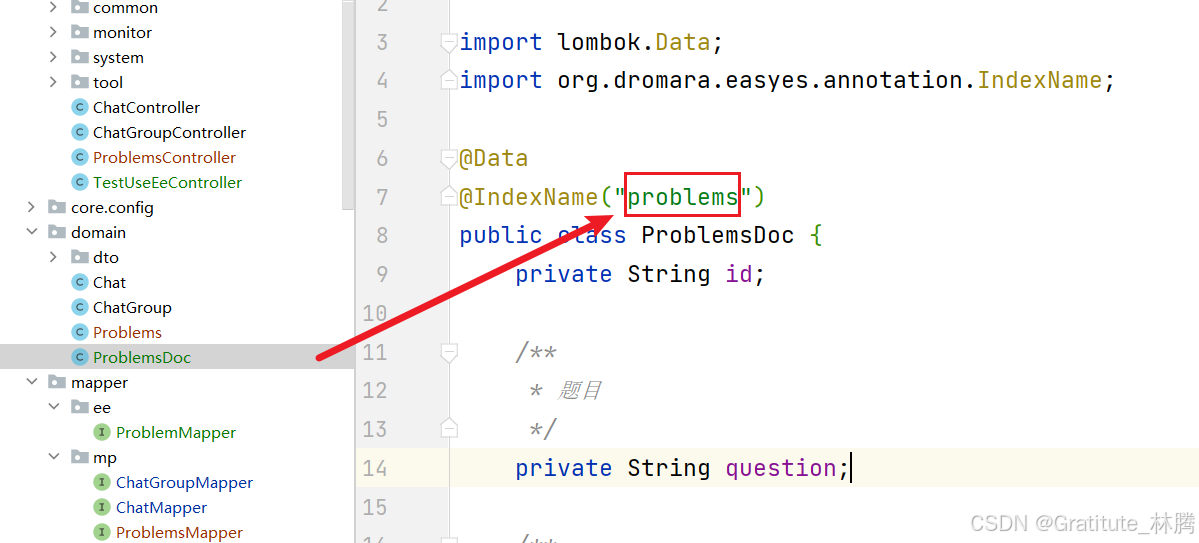
es-使用easy-es时如何指定索引库
在对应的实体类中,通过注解IndexName指定。 如上图,指定的索引库就是problems,那么之后我使用easy-es时都是针对该索引库进行增删改查。...

Redis-主从架构
主从架构 主从架构什么是主从架构基本架构 复制机制的工作原理1. 全量复制(Full Synchronization)2. 部分复制(Partial Synchronization)3. PSYNC2机制(Redis 4.0) 主从架构的关键技术细节1. 复制积压缓冲区…...

Java数据结构第二十期:解构排序算法的艺术与科学(二)
专栏:Java数据结构秘籍 个人主页:手握风云 目录 一、常见排序算法的实现 1.1. 直接选择排序 1.2. 堆排序 1.3. 冒泡排序 1.4. 快速排序 一、常见排序算法的实现 1.1. 直接选择排序 每⼀次从待排序的数据元素中选出最小的⼀个元素,存放在…...

inkscape裁剪svg
参考https://blog.csdn.net/qq_46049113/article/details/123824888,但是上个博主没有图片,不太直观,我补上。 使用inkscape打开需要编辑的图片。 在左边导航栏,点击矩形工具,创建一个矩形包围你想要保留的内容。 如果…...

类加载器加载过程
今天我们就来深入了解一下Java中的类加载器以及它的加载过程。 一、什么是类加载器? 在Java中,类加载器(Class Loader)是一个非常重要的概念。它负责将类的字节码文件(.class文件)加载到Java虚拟机&#x…...

Git基础之基本操作
文件的四种状态 Untracked:未追踪,如新建的文件,在文件夹中,没有添加到git库,不参与版本控制,通过git add将状态变为staged Unmodify:文件已入库,未修改,即版本库中的文件…...

简单的 Python 示例,用于生成电影解说视频的第一人称独白解说文案
以下是一个简单的 Python 示例,用于生成电影解说视频的第一人称独白解说文案。这个示例使用了 OpenAI 的 GPT 模型,因为它在自然语言生成方面表现出色。 实现思路 安装必要的库:使用 openai 库与 OpenAI API 进行交互。设置 API 密钥&#…...

[Pycharm]创建解释器
仅以此文章来记录自己经常脑子抽忘记的地方 有时候我们在建好了一个项目以后,想要更换解释器。以新建conda解释器为例。 一、conda解释器 1.选择setting 2.选择Add Local Interpreter 3.type选则conda。如果你之前已经有了conda环境,和我一样选择了Gen…...

在 k8s中查看最大 CPU 和内存的极限
在 Kubernetes(k8s)中,你可以从不同层面查看最大 CPU 和内存的极限,下面为你详细介绍从节点和集群层面查看的方法。 查看节点的 CPU 和内存极限 节点的 CPU 和内存极限是指单个节点上可分配的最大资源量,可通过以下几…...

【Python】为什么要写__init__.py
文章目录 PackageA(__init__特性)应该往__init__.py里放什么东西?1、包的初始化2、管理包的公共接口3、包的信息 正常我们直接导入就可以执行,但是在package的时候,有一种__init__.py的特殊存在 引入moduleA.py,执行main.py&…...

【IPFS应用开发】IPFS播放器-上传助手
本系列文章是针对 https://blog.csdn.net/weixin_43668031/article/details/83962959 内容的实现所编写的。开发经历包括思考过程、重构和推翻重来。 基于IPFS的视频播上传助手发布 起源一、优势:二、劣势:三、未来展望:上传助手Demo版本发布公告欢迎体验!立即体验:http:/…...

单细胞多数据集整合和去除批次效应教程,代做各领域生信分析
单细胞多数据集整合和去除批次效应教程 每个数据集的数据分别单独进行读取单细胞数据构建Seurat分析对象 读取各种来源的单细胞数据构建Seurat分析对象的教程 做这一步的时候可以查看我这篇写的非常详细的教程文章: 【腾讯文档】单细胞分析步骤1读取各种来源格式…...
)
Windows控制台函数:移动光标位置函数SetConsoleCursorPosition()
目录 什么是 SetConsoleCursorPosition? 它长什么样? 什么是 COORD? 怎么用它? 它有什么用? 跟 C 标准库有什么不一样? 注意事项 再试一个有趣的例子 什么是 SetConsoleCursorPosition?…...

MyBatis-Plus 注解大全
精心整理了最新的面试资料和简历模板,有需要的可以自行获取 点击前往百度网盘获取 点击前往夸克网盘获取 MyBatis-Plus 注解大全 MyBatis-Plus 是基于 MyBatis 的增强工具,通过注解简化了单表 CRUD 操作和复杂查询的配置。以下是常用注解的分类及详细说…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...

适应性Java用于现代 API:REST、GraphQL 和事件驱动
在快速发展的软件开发领域,REST、GraphQL 和事件驱动架构等新的 API 标准对于构建可扩展、高效的系统至关重要。Java 在现代 API 方面以其在企业应用中的稳定性而闻名,不断适应这些现代范式的需求。随着不断发展的生态系统,Java 在现代 API 方…...

React父子组件通信:Props怎么用?如何从父组件向子组件传递数据?
系列回顾: 在上一篇《React核心概念:State是什么?》中,我们学习了如何使用useState让一个组件拥有自己的内部数据(State),并通过一个计数器案例,实现了组件的自我更新。这很棒&#…...


