【概念梳理】激活函数
一、引言
常用的激活函数如下:
1、Sigmoid函数
2、Tanh函数
3、ReLU函数
4、ELU函数
5、PReLU函数
6、Leaky ReLU函数
7、Maxout函数
8、Mish函数
二、激活函数的定义
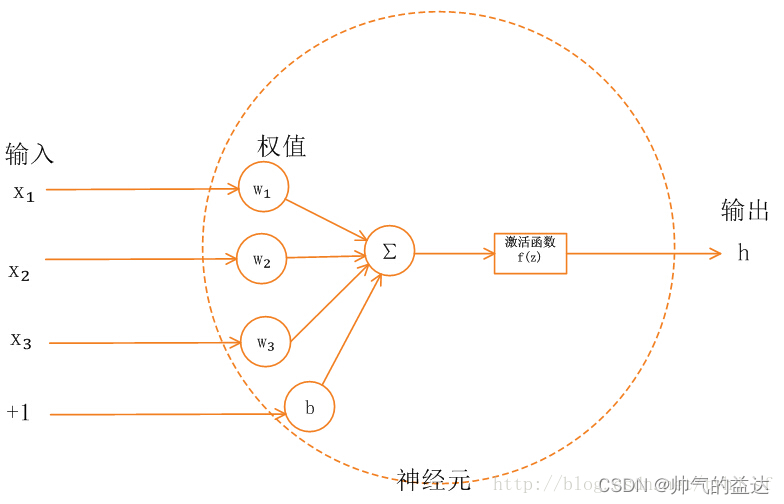
多层神经网络中,上层节点的输出和下层节点的输入之间具有一个函数关系,这个函数称为激活函数(Activation Function)。
三、激活函数的作用
一句话总结:为了提高模型的表达能力。
激活函数能让中间输出多样化,从而能够处理更复杂的问题。如果不使用激活函数,那么每一层的输出都是上一层输入的线性函数,最后的输出也只是最开始输入数据的线性组合而已。而激活函数可以给神经元引入非线性因素,当加入到多层神经网络时,就可以让神经网络拟合任何线性函数或非线性函数,从而使得网络可以适合更多的非线性问题,而不仅仅是线性问题。
激活函数被定义为一个几乎处处可微的函数。
四、饱和的概念
当函数满足limx→+∞f′(x)=0\ lim_{x\to+\infty}f'(x)=0 limx→+∞f′(x)=0时,称为右饱和;
当函数满足limx→−∞f′(x)=0\ lim_{x\to-\infty}f'(x)=0 limx→−∞f′(x)=0时,称为左饱和;
当f(x)\ f(x) f(x)同时满足左饱和和右饱和时,称为饱和
在饱和定义的基础上,如果存在常数C1\ C1 C1,当x>C1\ x >C1 x>C1时,恒满足f′(x)=0\ f'(x)=0 f′(x)=0,称为右硬饱和;同样,如果存在常数C2\ C2 C2,当x<C2\ x <C2 x<C2时,恒满足f′(x)=0\ f'(x)=0 f′(x)=0,称为左硬饱和
相对的,只有当x\ x x趋于极值时,f′(x)=0\ f'(x)=0 f′(x)=0,则称为软饱和。
五、常用的激活函数
1、Sigmod函数
Sigmoid 是常用的非线性的激活函数,它的数学形式如下:
f(x)=11+e−x\ f(x) = \frac{1}{1+e^{-x}} f(x)=1+e−x1
Sigmoid的几何图像如下:
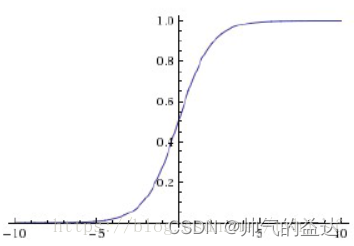
特点:
它能够把输入的连续实值映射为0和1之间的输出,特别的,如果是非常大的负数,输出就是0;如果是非常大的正数,输出就是1。
优点:
(1)单调递增,容易优化;
(2)求导容易。
缺点:
(1)Sigmod函数是软饱和,容易产生梯度消失;
(2)求导收敛速度慢;
(3)幂运算导致训练耗时。
Sigmod函数导数如下:
f′(x)=f(x)(1−f(x))\ f'(x)=f(x)(1-f(x)) f′(x)=f(x)(1−f(x))
导数的集合图像
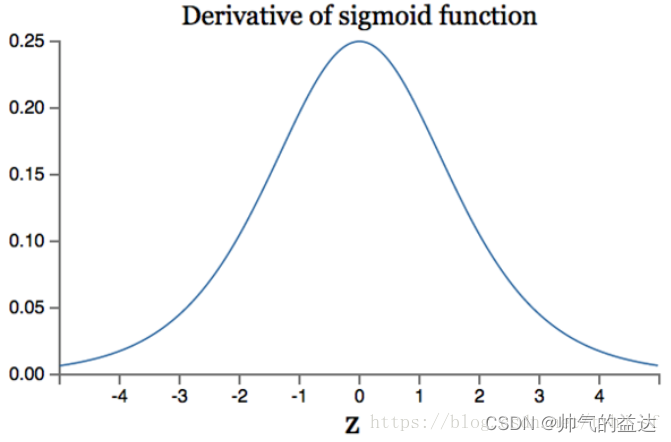
2、Tanh函数
tanh函数为双切正切函数,过(0,0)点,数学形式如下:
f′(x)=sinh(x)cosh(x)=1−e−2x1+e−2x=ex−e−xex+e−x=e2x−1e2x+1=2Sigmod(x)−1\ f'(x)=\frac{sinh(x)}{cosh(x)}=\frac{1-e^{-2x}}{1+e^{-2x}}=\frac{e^x-e^{-x}}{e^x+e^{-x}}=\frac{e^{2x}-1}{e^{2x}+1}=2Sigmod(x)-1 f′(x)=cosh(x)sinh(x)=1+e−2x1−e−2x=ex+e−xex−e−x=e2x+1e2x−1=2Sigmod(x)−1
tanh函数及其导数的几何图像如下图:
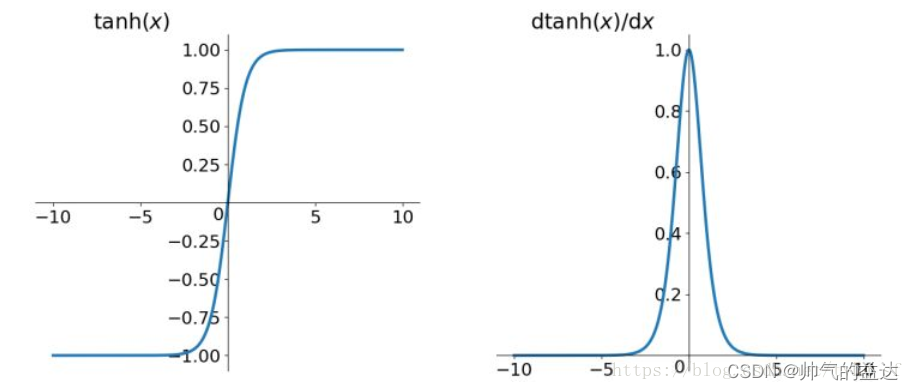
tanh读作Hyperbolic Tangent,它解决了Sigmoid函数的不是零均值(zero-centered)输出的问题。然而,梯度消失(gradient vanishing)的问题和幂运算导致的耗时问题仍然存在。
优点:
(1)收敛速度相比Sigmod快
缺点:
(1)未能解决梯度消失的问题
3、ReLU函数
ReLU函数的数学形式如下:
f(x)=max(0,x)={0,x≤0x,x>0\ f(x)=max(0,x)=\begin{cases} 0,&x\leq0\\ x,&x>0 \end{cases} f(x)=max(0,x)={0,x,x≤0x>0
ReLU函数及其导数的几何图像如下图:
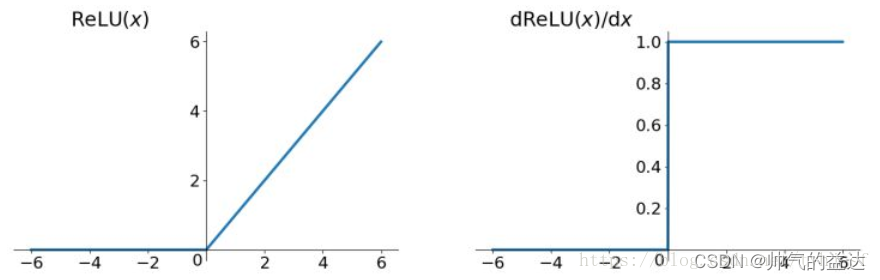
优点:
(1)收敛速度快与Sigmod函数和Tanh函数;
(2)有效缓解了梯度消失问题(在正区间);
(3)训练耗时优于Sigmod函数和Tanh函数;
(4)对神经网络可以使用稀疏表达;
缺点:
(1)在训练过程中容易出现神经元死亡(Dead ReLU Problem),之后梯度永远为0。
产生该问题的原因有两点:
(1)非常不幸的参数初始化,这种情况比较少见;
(2)学习率(learning rate)太大导致在训练过程中参数更新幅度太大,不幸使网络进入这种状态。解决方法是可以采用Xavier初始化方法,以及避免将学习率设置太大或使用adagrad等自动调节学习率的优化算法。
4、ELU函数
ELU函数(Exponential Linear Units)的数学形式如下:
f(x)=max(α(ex−1),x)={x,x>0α(ex−1),x≤0\ f(x)=max(\alpha(e^x-1),x)=\begin{cases} x,& x>0 \\ \alpha(e^x-1),&x\le0\end{cases} f(x)=max(α(ex−1),x)={x,α(ex−1),x>0x≤0
其中,α\ \alpha α是可学习的参数。
ELU函数及其导数的几何图像如下图:
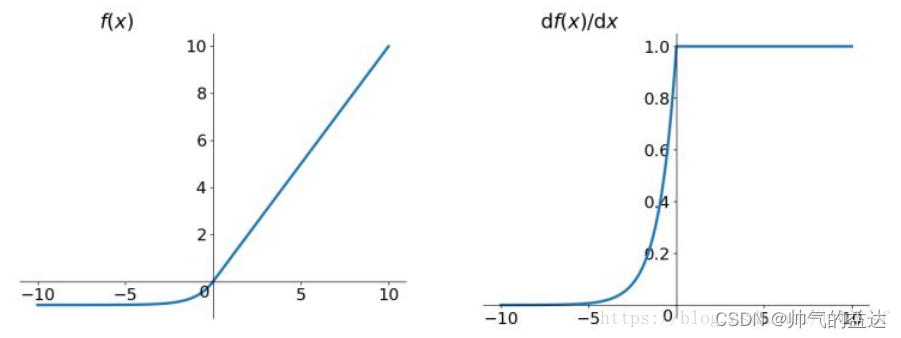
优点:
(1)ELU是为解决ReLU存在的问题而提出,显然,ELU有ReLU的基本所有优点,并可以消除ReLU中神经元死亡问题,在输入为负数时,具有一定输出,而且这部分输出具有一定的抗干扰能力。
缺点:
(1)幂运算增加了训练耗时。
5、PReLU函数
PReLU函数的数学形式如下:
f(x)=max(αx,x)={x,x>0αx,x≤0\ f(x)=max(\alpha x,x)=\begin{cases} x,& x>0 \\ \alpha x,&x\le0\end{cases} f(x)=max(αx,x)={x,αx,x>0x≤0
其中,α\ \alpha α是可学习的参数。
优点:
(1)相比于ELU函数,PReLU函数在负数区域是线性的,斜率虽小,但不会趋于0,因为没有了幂运算,训练速度也会快一些。
6、Leaky ReLU函数
Leaky ReLU函数的数学形式如下:
f(x)=max(0.01x,x)={x,x>00.01x,x≤0\ f(x)=max(0.01 x,x)=\begin{cases} x,& x>0 \\ 0.01 x,&x\le0\end{cases} f(x)=max(0.01x,x)={x,0.01x,x>0x≤0
Leaky ReLU函数及其导数的几何图像如下图:
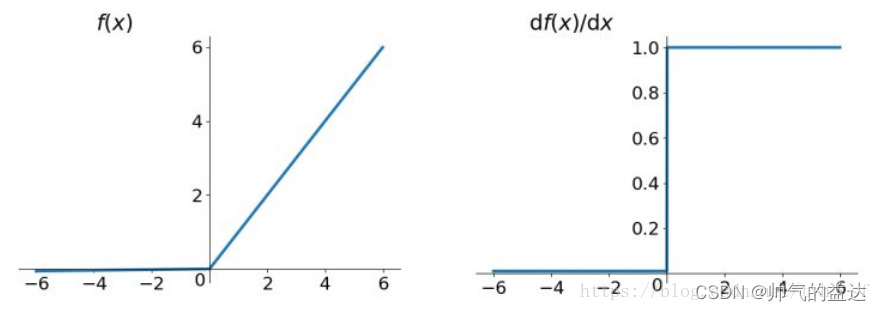
相比于PReLU函数,当α\ \alpha α为0.01时,PReLU函数就变成了Leaky ReLU函数了。
7、Maxout函数
待更新
8、Mish函数
Leaky ReLU函数的数学形式如下:
f(x)=x∗tanh(ln(1+ex))\ f(x)=x*tanh(ln^{(1+e^x)}) f(x)=x∗tanh(ln(1+ex))
Mish函数及其导数的几何图像如下图:
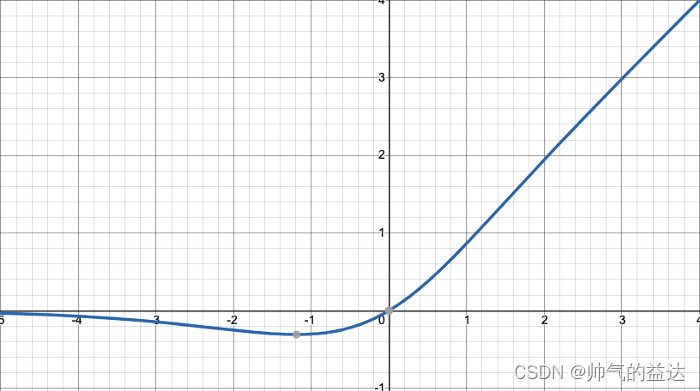
这与另一个被称为Swish函数的激活函数非常相似,Swish函数的数学形式如下:
f(x)=x∗Sigmoid(x)\ f(x)=x*Sigmoid(x) f(x)=x∗Sigmoid(x)
Mish函数及其导数的几何图像如下图:
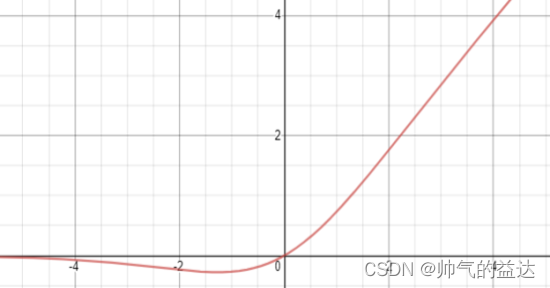
Mish函数是YOLOv4中使用的激活函数,原因是它的低成本和它的平滑、非单调、上无界、有下界等特点。
Mish函数的性能详细说明如下:
(1)无上界有下界:无上界是任何激活函数都需要的特性,因为它避免了导致训练速度急剧下降的梯度饱和,可加快训练过程。有下界属性有助于实现强正则化效果,适当的拟合模型(Mish的这个性质类似于ReLU和Swish的性质,其范围是(≈0.31,+∞]\ (\approx0.31,+\infty] (≈0.31,+∞]);
(2)非单调函数:这种性质有助于保持小的负值,从而稳定网络梯度流。大多数常用的激活函数,如ReLU、 Leaky ReLU,由于其差分为0,不能保持负值,因此大多数神经元没有得到更新;
(3)无穷阶连续性和光滑性:Mish是光滑函数,具有较好的泛化能力和结果的有效优化能力,可以提高结果的质量。在图中,可以看到ReLU和Mish之间的一个随机初始化的神经网络在宏观平滑度上的剧烈变化。然而,在Swish和Mish的情况下,宏观上或多或少还是相似的;
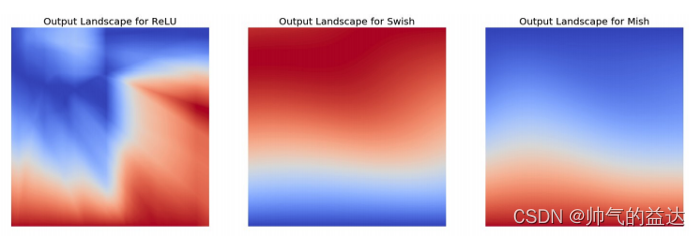
(4)计算量较大,但是效果更好:与ReLU相比,它的计算量比较大,但在深度神经网络中显示了比ReLU更好的结果。
(5)自门控:此属性受到Swish函数的启发,其中标量输入被提供给gate。它优于像ReLU这样的点式激活函数,后者只接受单个标量输入,而不需要更改网络参数。
参考资料
1、常用激活函数(激励函数)理解与总结
2、YOLOv4 中的 Mish 激活函数
声明
本博客的目的仅为学习交流和记录,谢谢大家的浏览。
相关文章:

【概念梳理】激活函数
一、引言 常用的激活函数如下: 1、Sigmoid函数 2、Tanh函数 3、ReLU函数 4、ELU函数 5、PReLU函数 6、Leaky ReLU函数 7、Maxout函数 8、Mish函数 二、激活函数的定义 多层神经网络中,上层节点的输出和下层节点的输入之间具有一个函数关系,…...

【python】@property 和 @staticmethod
property 和 staticmethod 是 Python 中的两个装饰器,它们分别用于在类中创建属性或静态方法。它们的作用如下: property property:用于将类的一个方法作为属性访问。在 Python 中,使用“getter” 和“setter”方法来实现属性&a…...
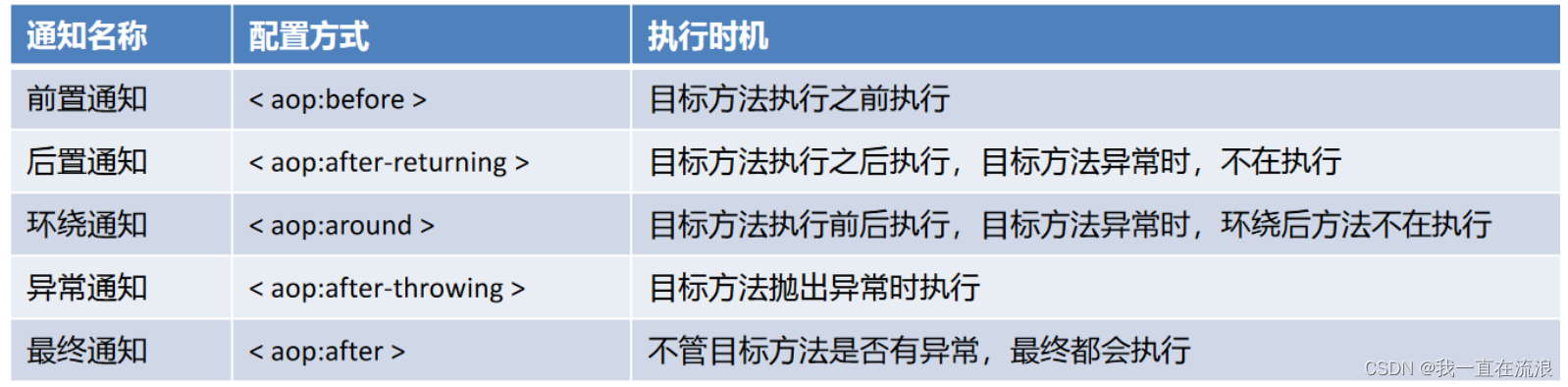
Spring题集 - Spring AOP相关面试题总结
文章目录01. Spring AOP 的理解?02. Spring AOP 思想的代码实现03. Spring AOP 的相关术语有哪些?04. Spring AOP 基于注解的切面实现?05. Spring AOP 的通知有哪些类型?06. AOP 有哪些实现方式?07. Spring AOP 和 AspectJ AOP 有…...

分考场
[蓝桥杯 2017 国 C] 分考场(假题:最小色数) 题目描述 nnn 个人参加某项特殊考试。 为了公平,要求任何两个认识的人不能分在同一个考场。 求最少需要分几个考场才能满足条件。 输入格式 第一行,一个整数 n(1<n<100)n(1<n<100…...

BI技巧丨DAX Studio
DAX Studio DAX Studio,作为PowerBI外部插件使用率排名第一的插件,相信各位小伙伴或多或少都听说过,那么DAX Studio具体有哪些功能呢? PS:DAX Studio的下载链接,小伙伴们可以自行搜索,这里就不…...

Java 8常用时间 API
Date: 你不爱我了吗? 🚡本地时间时区相关格式化在Java 8中,Instant类用于表示时间戳,相当于旧的Date类;LocalDateTime类用于表示日期和时间,相当于旧的Calendar类;DateTimeFormatter类用于格式化日期和时间…...

C++运算符
C运算符 运算符是一种告诉编译器执行特定的数学或逻辑操作的符号。C 内置了丰富的运算符,并提供了以下类型的运算符: 算术运算符关系运算符逻辑运算符位运算符赋值运算符杂项运算符 1. 算术运算符 运算符描述实例把两个操作数相加A B 将得到 30-从第…...

低/无代码赋能企业,IT与业务的角色正在悄然改变
现在这个社会,年轻人的压力是真的大,需要会的技能多到数不清。想学习多点技能也不知道去哪学,主要是网络资源太丰富,很难找到一个适合自己的。那接下来推荐4个大神级别的资源网站你可一定得码住,都是年轻人特别 …...

SpringCloud学习2(Spring Cloud Netflix)负载均衡Ribbon、Feign负载均衡、Hystix服务熔断
文章目录负载均衡RibbonRibbon的作用代码实现生产者cloud1_provider实现配置文件在HiController中编写以下代码启动集群消费者cloud1_consumer实现引入依赖编写配置文件编写启动类,并给RestTemplate配置LoadBalanced注解编写RestController来测试Feign负载均衡简介F…...
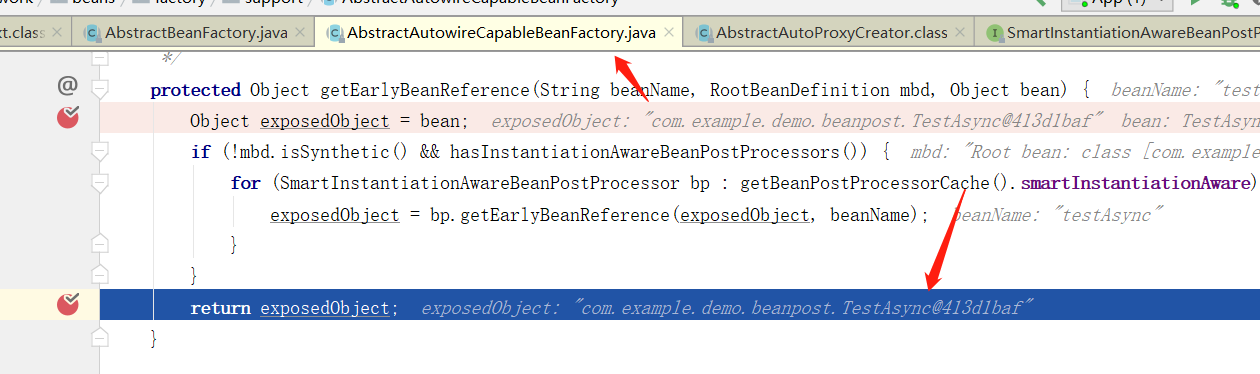
Spring 源码解析 - @Async 注解下的循环依赖问题原理
一、Async 注解下的循环依赖问题 我们都知道 Spring IOC 单例模式下可以帮助我们解决循环依赖问题,比如下面自己依赖自己循环依赖的场景: Component public class TestAsync {ResourceTestAsync async;public void test() {System.out.println("t…...

8个全球性编程比赛,天才程序员的梦想舞台
很多编程爱好者在学习之初,都渴望与全球的程序员一较高下,以证明自己的实力。 一些全球性的编程竞赛为他们提供了这样的机会,不仅可以与全世界的顶尖程序员们交流,还有机会获得丰厚的奖金和进入顶级公司的机会,更重要…...
2023年中国海洋大学计算机及电子信息考研分析
考研时间跨度: 初试时间: 2022年8月23 海大推免及创新人才计划接收通知。 2022年9月13 海大专业目录及人数,包含推免。 2022年10月18 2022年硕士研究生计划 ,不含推免。 海大2022年硕士研究生计划 网上第一次时间为2022年9月24日…...

【C++笔试强训】第六天
选择题 1. 解析:十进制转换为八进制就是不断的除8,取余数。十进制转换成其他进制的数就是除以进制,取余。 解析:注意printf的转换,%%只会打印一个%,所以选A。 解析:由于()的原因p先和*结合&…...

Redission 中的 RedLock 原理实现, springboot 你造吗?
分布锁之RedLock 锁住你的心我的爱 🚂为什么需要使用 RedLock锁被误释放时钟不一致问题锁的“延迟释放”而不是死锁Redlock是啥redlock 存在什么问题惊群效应时钟漂移Redisson 实现 RedLock在 Redisson 中, RedLock的实现类是哪一个类?这一招叫抛砖引玉springboot …...

【沐风老师】3dMax一键房屋创建者插件使用方法详解
3dmax一键房屋创建者,一键生成墙体、窗洞和门洞的插件!这个脚本主要用于创建或捕获一些架构项目所代表的平面,这是通过导入它们并在每个所需的层添加值来实现的。传统方法,但是省事儿多了! 【版本要求】 3dMax 2015及…...

C/C++ 变量详解
文章目录前言一、静态变量与动态变量1. 概念2. 区别3. 使用方法和注意事项3.1 静态变量3.2 动态变量4. 结论二、全局变量与局部变量1. 区别2. 全局变量的使用方法和注意事项3. 局部变量的使用方法和注意事项4. 总结前言 对C学习感兴趣的可以看看这篇文章哦:C/C教程…...

新SSD盘安装操作系统启动不了
今天打算给电脑升级下装备,加装一块固态硬盘。 电脑原本自带两块硬盘(SSD128GSATA1T),SSD清理了许久还是没空间,于是就买了块1TSSD,打算扩容下。 打开电脑后盖傻眼了,没有备用插槽,…...

基于Spring、SpringMVC、MyBatis的病历管理系统
文章目录 项目介绍主要功能截图:登录首页医院公告管理用户管理科室信息管理医生管理出诊信息管理预约时间段管理预约挂号管理门诊病历管理就诊评价管理轮播图管理功能架构图部分代码展示设计总结项目获取方式🍅 作者主页:Java韩立 🍅 简介:Java领域优质创作者🏆、 简历…...

QT编程从入门到精通之三十四:“第五章:Qt GUI应用程序设计”之“5.5 Qt Creator使用技巧”
目录 第五章:Qt GUI应用程序设计 5.5 Qt Creator使用技巧 第五章:Qt GUI应用程序设计 在“Qt 程序创建基础”上,本章将继续深入地介绍Qt Creator设计GUI应用程序的方法,包括Qt创建的应用程序项目的基本组织结构,可视化设计的UI界面文件的原理和运行机制,信号与槽的使用…...

网络工程方向有哪些SCI期刊推荐? - 易智编译EaseEditing
以下是网络工程领域的一些SCI期刊推荐: IEEE Transactions on Network and Service Management: 这是一个IEEE旗下的期刊,涵盖了网络与服务管理方面的研究。主要关注网络管理、服务管理和其它相关领域的创新和最新研究。 Computer Networks: 这是一本著…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...

JS手写代码篇----使用Promise封装AJAX请求
15、使用Promise封装AJAX请求 promise就有reject和resolve了,就不必写成功和失败的回调函数了 const BASEURL ./手写ajax/test.jsonfunction promiseAjax() {return new Promise((resolve, reject) > {const xhr new XMLHttpRequest();xhr.open("get&quo…...

MySQL 主从同步异常处理
阅读原文:https://www.xiaozaoshu.top/articles/mysql-m-s-update-pk MySQL 做双主,遇到的这个错误: Could not execute Update_rows event on table ... Error_code: 1032是 MySQL 主从复制时的经典错误之一,通常表示ÿ…...
