【C++笔试强训】第六天
选择题
1.
解析:十进制转换为八进制就是不断的除8,取余数。十进制转换成其他进制的数就是除以进制,取余。
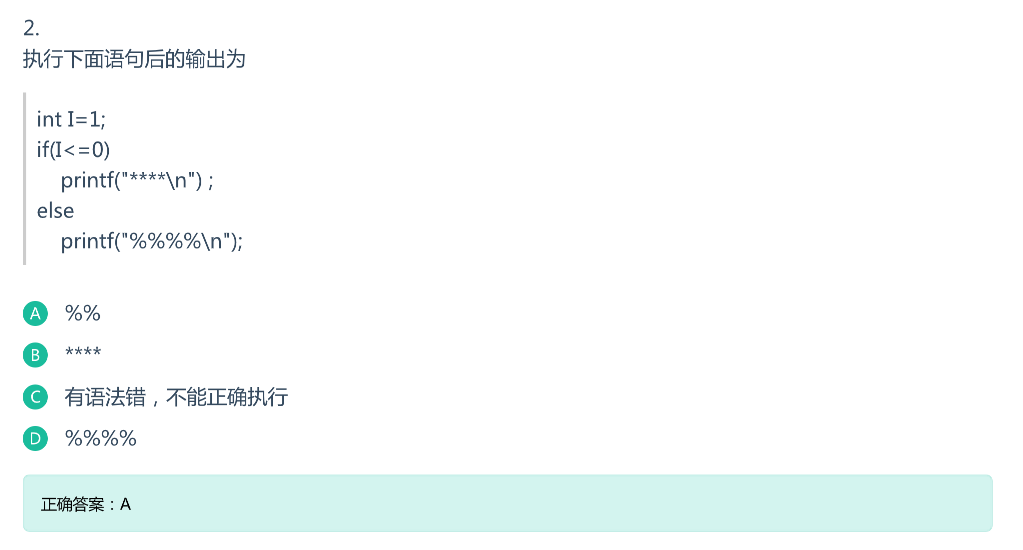
解析:注意
printf的转换,%%只会打印一个%,所以选A。

解析:由于
()的原因p先和*结合,说明p是一个指针,char (*p)[16]是一个数组指针,指向一个char类型的字符数组,该数组中有16个元素。

解析:a表示首元素的地址,对与二维数组,首元素是第0行数组的地址。明显D选项还是一个地址。

解析:
define是直接替换其所在位置就行,替换之后正常计算就可以,注意优先级就可以。
解析:

解析:free之后不会自动的把指针变量制成NULL,需要手动处理。

解析:题目中为二维数组,数组名表示数组首元素的地址,
a是二维数组数组名,表示数组首元素的地址,在二维数组中,数组首元素的地址即第一行的地址,第一行的数组名可以用a[0]表示;*(a+1)可以表示成*(&a[0]+1),&a[0]是int(*)[5]类型,+1之后到二维数组的第二行,所以*(a+1)就是a[1],a[1]就是第二行数组名,也表示第二行首元素的地址&a[1][0];+2是向后移动2个int*类型的大小。所以选B。

解析:64位编译器下指针大小为8个字节大小,所以a4占8个字节大小;a1(0 ~ 7),a2(8~ 9),浪费(10 ~ 11),a3(12~ 15),a4(16~23),共24个字节的大小,也是最大对齐数8的整型倍。选A。

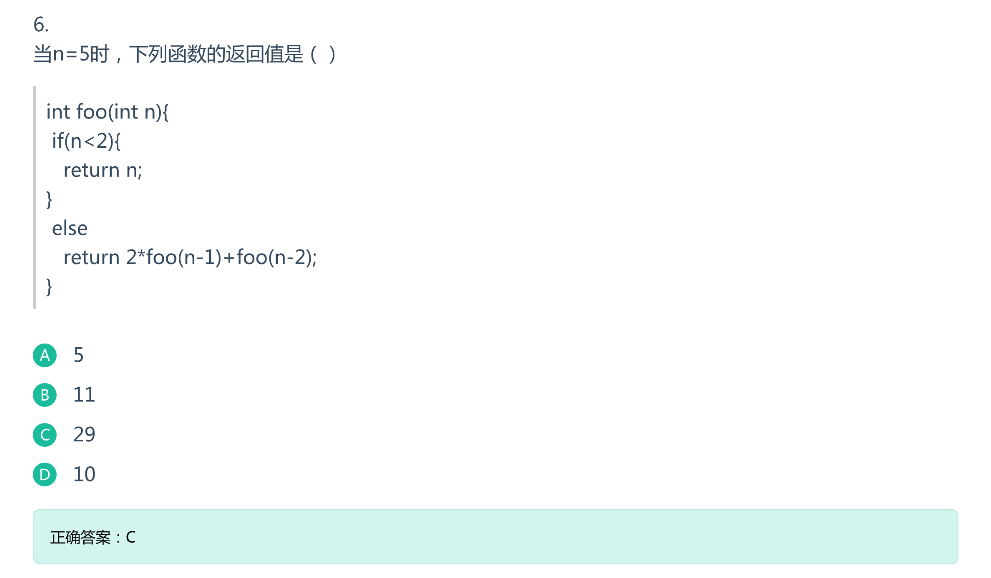
解析:本题考查递归,递归类题目可以通过画图来解决。
编程题
1.不要二

解析:这里理解输入顺序为行、列。
( (x1-x2) * (x1-x2) + (y1-y2) * (y1-y2) ) == 4 1 + 3 = 4 3 + 1 = 4 2 + 2 = 4 0 + 4 = 4 4 + 0 = 4 前三种情况都不存在 只能是x1=x2 (y1-y2) = 2 或者 y1=y2 x1-x2 = 2 假设数组全是1,经过上面的公式变换之后 1 1 1 1 1 1 --> 1 1 1 1 0 0 也就是v[i][j]和v[i+2][j]、v[i][j]和v[i][j+2] 只能有一个有蛋糕
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;int main() {int row,col;//row行,col列cin >> row >> col;vector<vector<int>> a; //设定一个二维数组a.resize(row);//定义行数for(int i = 0; i < row; i++) //一行一行的进行初始化{a[i].resize(col,1);//全部初始化为1}int count = 0;for(int i = 0; i < row; i++){for(int j = 0; j < col; j++){if(a[i][j] == 1) //判单是否为1count++;if(i + 2 < row) //判断是否在二维数组之内a[i+2][j] = 0;if(j + 2 < col) //判断是否在二维数组之内a[i][j+2] = 0;}}cout << count;return 0;
}
// 64 位输出请用 printf("%lld")
答案解析:
本题看起来很难,实际是一个中等难度的题。本题如果没记错,是一个往年网易的笔试题,大家可以看到大厂的题的难度。
本题的重点是要读懂题意,并且需要多读两遍,才能读懂,本题本质就是在二维数组中每个坐标去放蛋糕,一个坐标位置放了蛋糕,跟他欧几里得距离为2的位置不能放蛋糕,这个就是关键点。对于两个格子坐标(x1,y1),(x2,y2)的欧几里得距离为: ( (x1-x2) * (x1-x2) + (y1-y2) * (y1-y2) ) 的算术平方根 。也就是说:如果(x1,y1)放了蛋糕,则满足 ( (x1-x2) * (x1-x2) + (y1-y2) * (y1-y2) ) == 4的(x2,y2)不能放蛋糕。
( (x1-x2) * (x1-x2) + (y1-y2) * (y1-y2) ) == 4看起来是一个无解的表达式。
但是可以进行加法表达式分解:
1+3=4
3+1=4
2+2=4
0+4=4
4+0=4
仔细分析前三个表达式是不可能的,因为(x1-x2) * (x1-x2)表达式结果不能等于2或3。也就是说( (x1-x2) * (x1-x2) 和(y1-y2) * (y1-y2) )两个表达式一个等于0,一个等于4.可以看出:假设放蛋糕的位置是(x1,y1),则不能放蛋糕的位置(x2,y2),满足x1==x2,y1-y2==2或者x1-x2==2,y1==y2。
【解题思路】:
仔细读理解了上面的题目解读,本题就非常简单了,使用vector<vector>定义一个二维数组,resize开空间并初始化,每个位置初始化为1,表示当蛋糕,a[i][j]位置放蛋糕,则可以标记处a[i][j+2]和a[i+1][j]位置不能放蛋糕,遍历一遍二维数组,标记处不能放蛋糕的位置,统计也就统计出了当蛋糕的位置数。
// 直接暴力计算,默认所有蛋糕的位置标记成1,不能放的地方标记成0
// 1 1 0 0 1 1
// 1 1 0 0 1 1
// 0 0 1 1 0 0
// 0 0 1 1 0 0
#include<iostream>
#include<vector>
using namespace std;
int main()
{int w,h,res = 0;cin >> w >> h;//w行,h列vector<vector<int>> a;a.resize(w);for(auto& e : a)e.resize(h, 1);for(int i=0;i<w;i++){for(int j=0;j<h;j++){if(a[i][j]==1){res++;// 标记不能放蛋糕的位置if((i+2)<w)a[i+2][j] = 0;if((j+2)<h)a[i][j+2] = 0;}}}cout << res;return 0;
}
2.把字符串转换成整数

解析:先检查字符串中是否有除数字字符及
'-'\'+'外的其他字符,如果有直接返回;如果没有,要先检查首个字符是否为'+'、'-',考虑如果为'-',需要设立一个flag进行标记,当第一个字符为'+'、'-'时,先忽视,对下一个位置开始的数字串进行处理,-'0'得到对应的数字,每次*10加上新的数字……在最后检查标记位,如果为true,说明第一个字符为'-',需要进行num = 0 - num处理,得到结果。
class Solution {public:bool IsWord(string str) { //检查字符串中是否有字母int i = 0;for (i = 1; i < str.size(); i++) {if ((str[i] >= 'a' && str[i] <= 'z') || (str[i] >= 'A' && str[i] <= 'Z')) {return false;}}return true;}int StrToInt(string str) {int i = 0;/*if (!IsWord(str)) {cout << "0";return 0;}*/for (i = 1; i < str.size();i++) {//从1开始检查字符串中受否有其他字符if ((str[i] < '0' ) || (str[i] > '9')) {cout << "0";return 0;}}i = 0;bool flag = false;//标记其首字符为+或者-if (str[0] == '-') {flag = true;//如果首字符为-则改变flag,同时i++i++;}if (str[0] == '+') {i++;//如果首字符为+不改变flag,但是i++}long long num = 0;//起始条件不能确定,因为不确定str[0]是否是+或者-还是直接数字开头for (i; i < str.size(); i++) {int nums = str[i] - '0';num = num * 10 + nums;}if (flag) {num = 0 - num;}cout << num;return num;}
};
答案解析:解题思路非常简单,就是上次计算的结果*10,相当于10进制进位,然后加当前位的值。
例如:“123”转换的结果是
sum=0 sum*10+1->1 sum*10+2->12 sum*10+3->123
本题的关键是要处理几个关键边界条件:
- 空字符串
- 正负号处理
- 数字串中存在非法字符
class Solution {
public:
int StrToInt(string str)
{if(str.empty())return 0;int symbol = 1;if(str[0] == '-') //处理负号{symbol = -1;str[0] = '0'; //这里是字符'0',不是0}else if(str[0] == '+') //处理正号{symbol = 1;str[0] = '0';}int sum = 0;for(int i=0;i<str.size();++i){if(str[i] < '0' || str[i] > '9'){}sum = sum *10 + str[i] - '0';}return symbol * sum;
}
};
相关文章:

【C++笔试强训】第六天
选择题 1. 解析:十进制转换为八进制就是不断的除8,取余数。十进制转换成其他进制的数就是除以进制,取余。 解析:注意printf的转换,%%只会打印一个%,所以选A。 解析:由于()的原因p先和*结合&…...

Redission 中的 RedLock 原理实现, springboot 你造吗?
分布锁之RedLock 锁住你的心我的爱 🚂为什么需要使用 RedLock锁被误释放时钟不一致问题锁的“延迟释放”而不是死锁Redlock是啥redlock 存在什么问题惊群效应时钟漂移Redisson 实现 RedLock在 Redisson 中, RedLock的实现类是哪一个类?这一招叫抛砖引玉springboot …...

【沐风老师】3dMax一键房屋创建者插件使用方法详解
3dmax一键房屋创建者,一键生成墙体、窗洞和门洞的插件!这个脚本主要用于创建或捕获一些架构项目所代表的平面,这是通过导入它们并在每个所需的层添加值来实现的。传统方法,但是省事儿多了! 【版本要求】 3dMax 2015及…...

C/C++ 变量详解
文章目录前言一、静态变量与动态变量1. 概念2. 区别3. 使用方法和注意事项3.1 静态变量3.2 动态变量4. 结论二、全局变量与局部变量1. 区别2. 全局变量的使用方法和注意事项3. 局部变量的使用方法和注意事项4. 总结前言 对C学习感兴趣的可以看看这篇文章哦:C/C教程…...

新SSD盘安装操作系统启动不了
今天打算给电脑升级下装备,加装一块固态硬盘。 电脑原本自带两块硬盘(SSD128GSATA1T),SSD清理了许久还是没空间,于是就买了块1TSSD,打算扩容下。 打开电脑后盖傻眼了,没有备用插槽,…...

基于Spring、SpringMVC、MyBatis的病历管理系统
文章目录 项目介绍主要功能截图:登录首页医院公告管理用户管理科室信息管理医生管理出诊信息管理预约时间段管理预约挂号管理门诊病历管理就诊评价管理轮播图管理功能架构图部分代码展示设计总结项目获取方式🍅 作者主页:Java韩立 🍅 简介:Java领域优质创作者🏆、 简历…...

QT编程从入门到精通之三十四:“第五章:Qt GUI应用程序设计”之“5.5 Qt Creator使用技巧”
目录 第五章:Qt GUI应用程序设计 5.5 Qt Creator使用技巧 第五章:Qt GUI应用程序设计 在“Qt 程序创建基础”上,本章将继续深入地介绍Qt Creator设计GUI应用程序的方法,包括Qt创建的应用程序项目的基本组织结构,可视化设计的UI界面文件的原理和运行机制,信号与槽的使用…...

网络工程方向有哪些SCI期刊推荐? - 易智编译EaseEditing
以下是网络工程领域的一些SCI期刊推荐: IEEE Transactions on Network and Service Management: 这是一个IEEE旗下的期刊,涵盖了网络与服务管理方面的研究。主要关注网络管理、服务管理和其它相关领域的创新和最新研究。 Computer Networks: 这是一本著…...
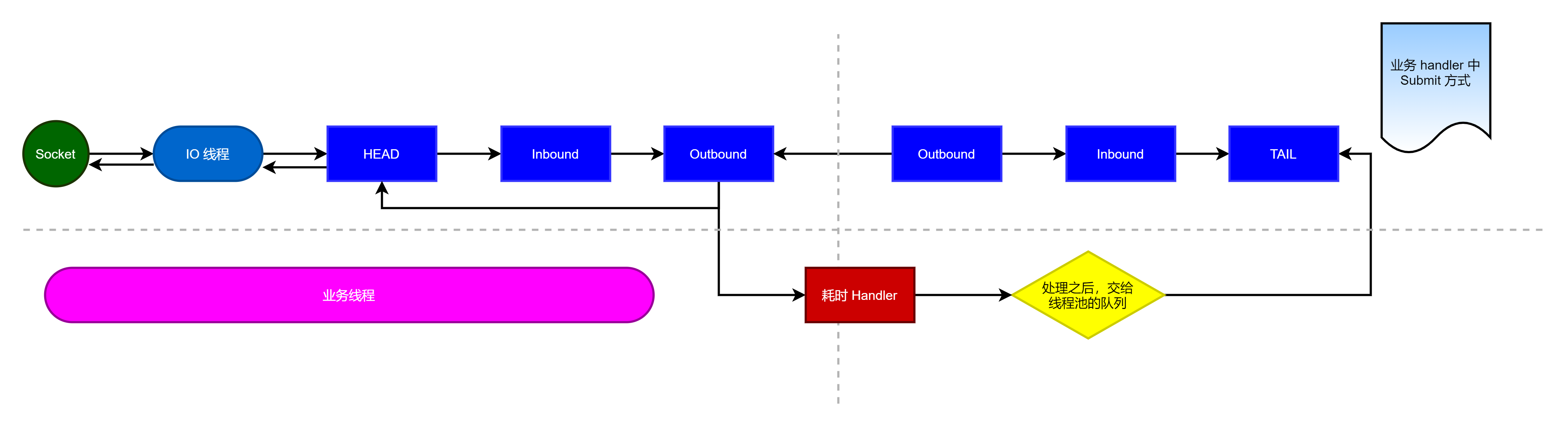
netty入门(二十六)任务加入异步线程池源码剖析
1.handler中加入线程池和Context添加线程池 1.1 源码剖析目的 (1)在 Netty 中做耗时的,不可预料的操作,比如:数据库、网络请求、会严重影响 Netty 对 Socket 的处理速度。 (2)而解决方法就是…...

神经网络算法入门和代码
文章内容 感知机(Perceptron)反向传播算法(Back Propagation algorithm)RBF(Radial Basis Function,径向基函数) 网络:单一层前馈网络,它使用径向基作为隐层神经元激活函数ART(Adaptive Resona…...

如何用一个端口同时暴露 HTTP1/2、gRPC、Dubbo 协议?
作者:华钟明 本文我们将介绍 Apache Dubbo 灵活的多协议设计原则,基于这一设计,在 Dubbo 框架底层可灵活的选用 HTTP/2、HTTP/REST、TCP、gRPC、JsonRPC、Hessian2 等任一 RPC 通信协议,同时享用统一的 API 与对等的服务治理能力。…...

ToBeWritten之杂项2
也许每个人出生的时候都以为这世界都是为他一个人而存在的,当他发现自己错的时候,他便开始长大 少走了弯路,也就错过了风景,无论如何,感谢经历 转移发布平台通知:将不再在CSDN博客发布新文章,敬…...
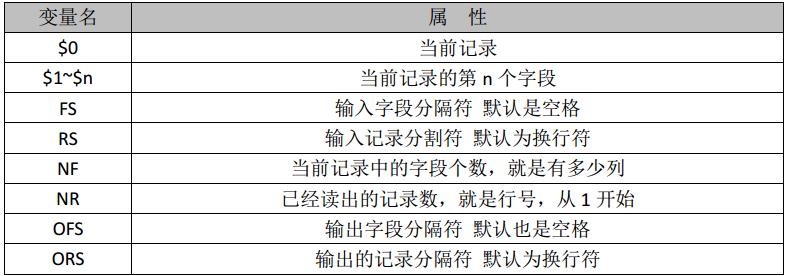
Linux三剑客之awk命令详解
1、概述 Linux三剑客:grep、sed、awk。grep主打查找功能,sed主要是编辑行,awk主要是分割列处理。本篇文章我们详细介绍awk命令。 awk其名称得自于它的创始人 Alfred Aho 、Peter Weinberger 和 Brian Kernighan 姓氏的首个字母。awk是一种编…...

C++异常处理:掌握高效、健壮代码的秘密武器
C异常处理全面解析:底层原理、编译器技巧与实用场景C异常机制:让我们迈向更安全、更可靠的代码C异常处理:掌握基本概念什么是异常?异常处理的重要性C异常处理的组成部分:try、catch、throw探索C异常处理的核心…...
Jetpack Compose基础组件之按钮组件
概述 按钮组件Button是用户和系统交互的重要组件之一,它按照Material Design风格实现,我们先看下Button的参数列表,通过参数列表了解下Button的整体功能 Composable fun Button(onClick: () -> Unit, // 点击按钮时的回调modifier: Modi…...
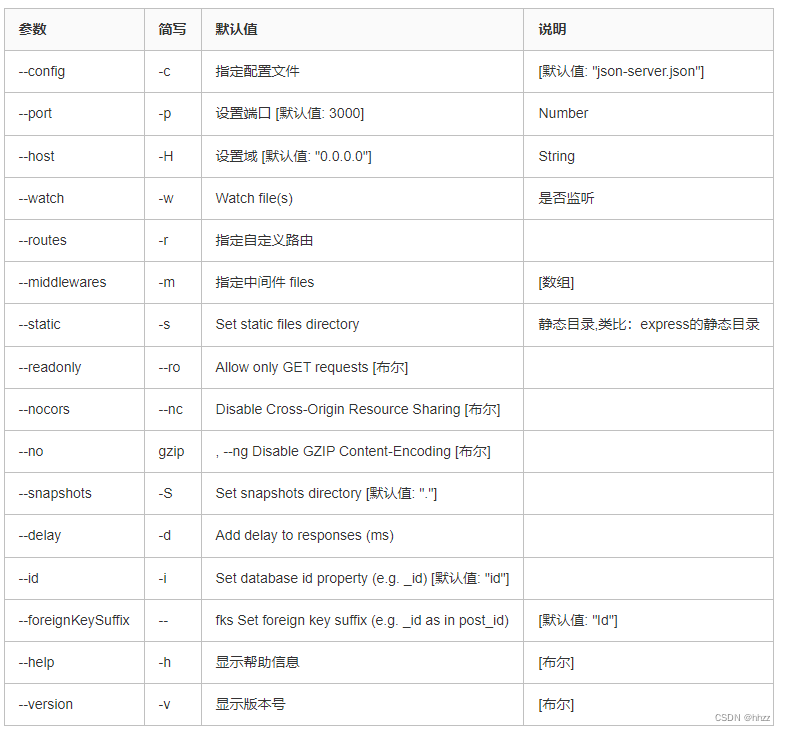
利用json-server快速在本地搭建一个JSON服务
1,json-server介绍 一个在前端本地运行,可以存储json数据的server。 通俗来说,就是模拟服务端接口数据,一般用在前后端分离后,前端人员可以不依赖API开发,而在本地搭建一个JSON服务,自己产生测…...
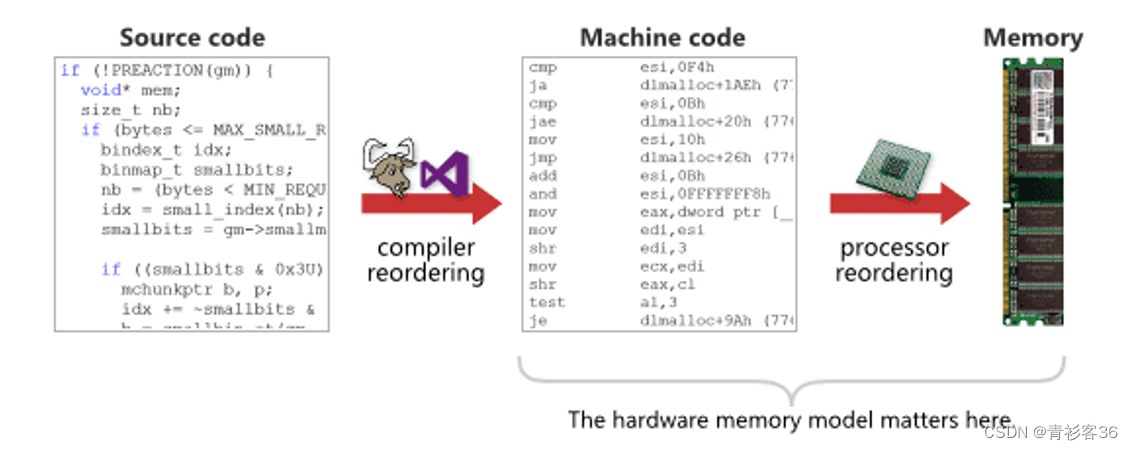
可重入函数与线程安全
指令乱序和线程安全 先来看什么是指令乱序问题以及为什么有指令乱序。程序的代码执行顺序有可能被编译器或CPU根据某种策略打乱指令执行顺序,目的是提升程序的执行性能,让程序的执行尽可能并行,这就是所谓指令乱序问题。理解指令乱序的策略是…...

一文彻底读懂异地多活
文章目录 系统可用性单机架构主从副本风险不可控同城灾备同城双活两地三中心伪异地双活真正的异地双活如何实施异地双活1、按业务类型分片2、直接哈希分片3、按地理位置分片异地多活总结系统可用性 要想理解异地多活,我们需要从架构设计的原则说起。 现如今,我们开发一个软件…...

孕酮PEG偶联物:mPEG Progestrone,PEG Progestrone,甲氧基聚乙二醇孕酮
中文名称:甲氧基聚乙二醇孕酮 英文名称:mPEG Progestrone,PEG Progestrone 一、反应机理: 孕酮-PEG衍生物是一类具有生物活性的类固醇-PEG偶联物,可用于药物发现或生物测定开发。孕酮是一种女性性激素,负…...
网络系统集成实验(一)| 网络系统集成基础
目录 一、前言 二、实验目的 三、实验需求 四、实验步骤与现象 (1)网络设置、网络命令的使用 ① 在华为设备中,常用指令的使用 ② 在思科设备中,常用指令的使用 ③ 在Windows设备中,常用网络指令的使用 …...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

PostgreSQL——环境搭建
一、Linux # 安装 PostgreSQL 15 仓库 sudo dnf install -y https://download.postgresql.org/pub/repos/yum/reporpms/EL-$(rpm -E %{rhel})-x86_64/pgdg-redhat-repo-latest.noarch.rpm# 安装之前先确认是否已经存在PostgreSQL rpm -qa | grep postgres# 如果存在࿰…...

手机平板能效生态设计指令EU 2023/1670标准解读
手机平板能效生态设计指令EU 2023/1670标准解读 以下是针对欧盟《手机和平板电脑生态设计法规》(EU) 2023/1670 的核心解读,综合法规核心要求、最新修正及企业合规要点: 一、法规背景与目标 生效与强制时间 发布于2023年8月31日(OJ公报&…...
:工厂方法模式、单例模式和生成器模式)
上位机开发过程中的设计模式体会(1):工厂方法模式、单例模式和生成器模式
简介 在我的 QT/C 开发工作中,合理运用设计模式极大地提高了代码的可维护性和可扩展性。本文将分享我在实际项目中应用的三种创造型模式:工厂方法模式、单例模式和生成器模式。 1. 工厂模式 (Factory Pattern) 应用场景 在我的 QT 项目中曾经有一个需…...