神经网络算法入门和代码
文章内容
- 感知机(Perceptron)
- 反向传播算法(Back Propagation algorithm)
- RBF(Radial Basis Function,径向基函数) 网络:单一层前馈网络,它使用径向基作为隐层神经元激活函数
- ART(Adaptive Resonance Theory,自适应谐振理论) 网络:竞争型学习无监督学习策略
- SOM(Self Organizing Map,自组织映射) 网络:竞争性学习型的无监督神经网络
- 级联相关(Cascade-Correlation) 网络:结构自适应网络
- Elman网络:递归网络
- Boltzmann机
一、 感知机(Perceptron)
1. 含义
一个感知器有如下组成部分:
- 输入权值:一个感知器可以接收多个输入x,每个输入上有一个权值w,此外还有一个偏置项b,就是上图中的。
- 激活函数:如阶跃函数(Step function),sigmoid函数
- 输出:y= f(wx+b)
- 权重更新:
,其中
,η为学习率
单层感知机只能解决线性可分的问题。而多层感知器可以拟合任何的线性函数,任何线性分类或线性回归问题都可以用感知器来解决。
2. 更新方法


3. 代码
class Perceptron(object):def __init__(self, input_num, activator):'''初始化感知器,设置输入参数的个数,以及激活函数。激活函数的类型为double -> double'''self.activator = activator# 权重向量初始化为0self.weights = [0.0 for _ in range(input_num)]# 偏置项初始化为0self.bias = 0.0def __str__(self):'''打印学习到的权重、偏置项'''return 'weights\t:%s\nbias\t:%f\n' % (self.weights, self.bias)def predict(self, input_vec):'''输入向量,输出感知器的计算结果'''# 把input_vec[x1,x2,x3...]和weights[w1,w2,w3,...]打包在一起# 变成[(x1,w1),(x2,w2),(x3,w3),...]# 然后利用map函数计算[x1*w1, x2*w2, x3*w3]# 最后利用reduce求和return self.activator(reduce(lambda a, b: a + b,map(lambda (x, w): x * w, zip(input_vec, self.weights)), 0.0) + self.bias)def train(self, input_vecs, labels, iteration, rate):'''输入训练数据:一组向量、与每个向量对应的label;以及训练轮数、学习率'''for i in range(iteration):self._one_iteration(input_vecs, labels, rate)def _one_iteration(self, input_vecs, labels, rate):'''一次迭代,把所有的训练数据过一遍'''# 把输入和输出打包在一起,成为样本的列表[(input_vec, label), ...]# 而每个训练样本是(input_vec, label)samples = zip(input_vecs, labels)# 对每个样本,按照感知器规则更新权重for (input_vec, label) in samples:# 计算感知器在当前权重下的输出output = self.predict(input_vec)# 更新权重self._update_weights(input_vec, output, label, rate)def _update_weights(self, input_vec, output, label, rate):'''按照感知器规则更新权重'''# 把input_vec[x1,x2,x3,...]和weights[w1,w2,w3,...]打包在一起# 变成[(x1,w1),(x2,w2),(x3,w3),...]# 然后利用感知器规则更新权重delta = label - outputself.weights = map(lambda (x, w): w + rate * delta * x,zip(input_vec, self.weights))# 更新biasself.bias += rate * delta训练和预测:
def f(x):'''定义激活函数f'''return 1 if x > 0 else 0
def get_training_dataset():'''基于and真值表构建训练数据'''# 构建训练数据# 输入向量列表input_vecs = [[1,1], [0,0], [1,0], [0,1]]# 期望的输出列表,注意要与输入一一对应# [1,1] -> 1, [0,0] -> 0, [1,0] -> 0, [0,1] -> 0labels = [1, 0, 0, 0]return input_vecs, labels
def train_and_perceptron():'''使用and真值表训练感知器'''# 创建感知器,输入参数个数为2(因为and是二元函数),激活函数为fp = Perceptron(2, f)# 训练,迭代10轮, 学习速率为0.1input_vecs, labels = get_training_dataset()p.train(input_vecs, labels, 10, 0.1)#返回训练好的感知器return p
if __name__ == '__main__': # 训练and感知器and_perception = train_and_perceptron()# 打印训练获得的权重print and_perception# 测试print '1 and 1 = %d' % and_perception.predict([1, 1])print '0 and 0 = %d' % and_perception.predict([0, 0])print '1 and 0 = %d' % and_perception.predict([1, 0])print '0 and 1 = %d' % and_perception.predict([0, 1])二、反向传播(BP)算法
1. 内容
- 权重和偏差
- 代价函数(cost function):均方误差
- 权重更新:梯度下降(gradient descent)策略
- 更多优化方法:"正则化",在误差目标函数中添加一个用于描述网络复杂度的部分(如w²)
2. 参数计算与更新
2.1 总误差

2.2 误差在隐藏层反向传播(输出层->隐藏层)
以权重参数w5为例,如果我们想知道w5对整体误差产生了多少影响,可以用整体误差对w5求偏导求出:(链式法则)

求三项偏导值:
![]()

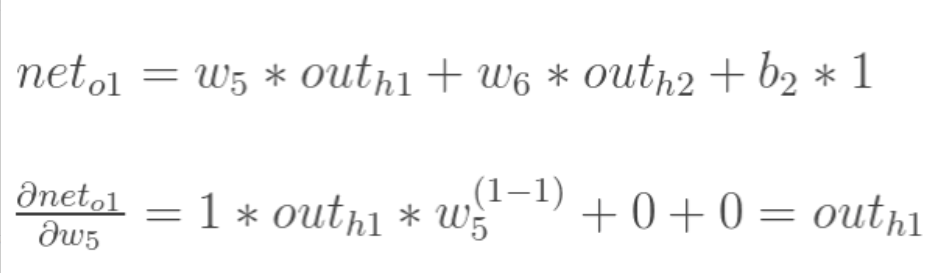
所以,我们得到:
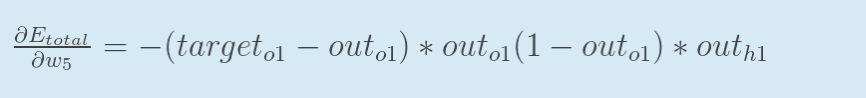
可以取符号δ简化公式(可选):
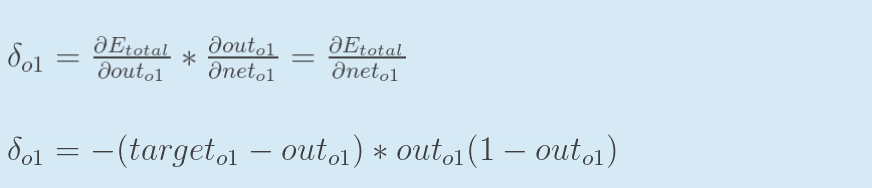

最后更新权重w:
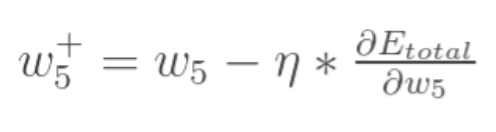
2.3 误差反向传播(隐藏层->隐藏层)
方法差不多,但要计算误差基于传递过来的之前的误差:
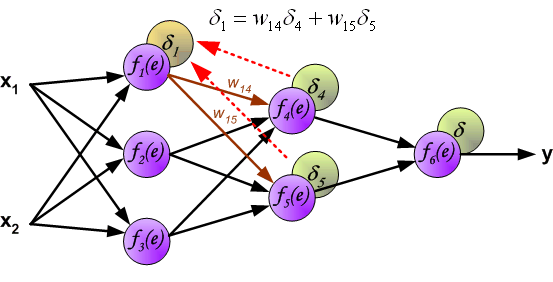
out(h1)会接受E(o1)和E(o2)两个地方传来的误差,所以这个地方两个都要计算。


最后,更新权重w1:

总结,前向传播和反向传播顺序说明图:
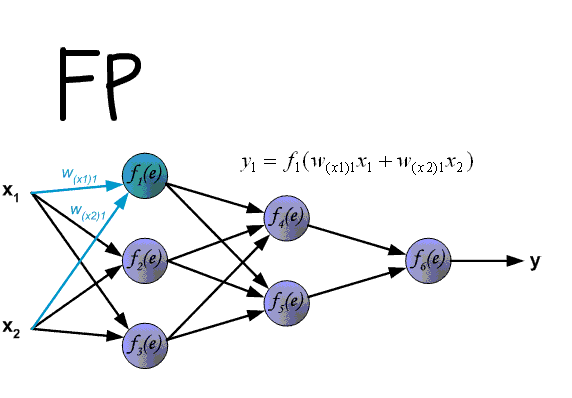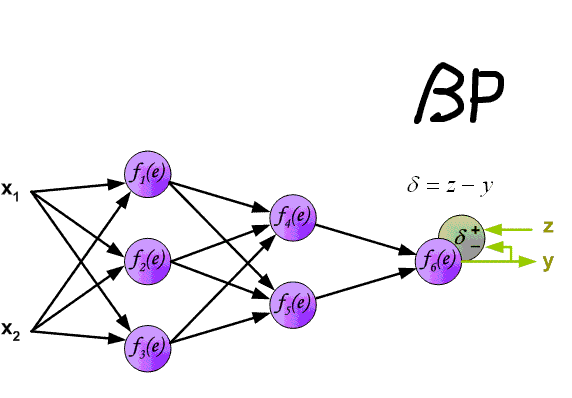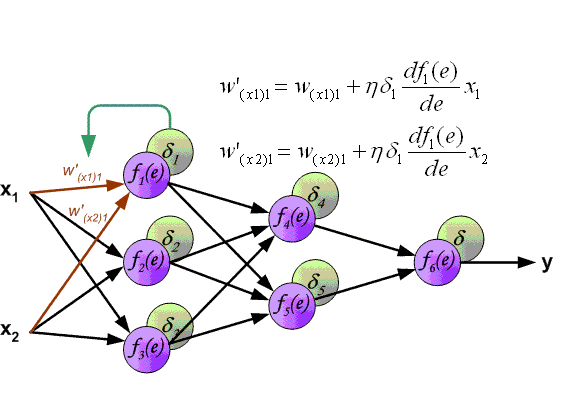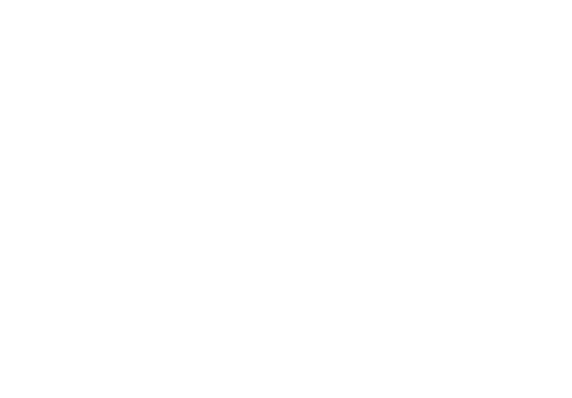
3. 随机梯度更新和批量更新
批量(batch)更新时,计算完一批样本后Δw再更新:

批量梯度下降和随机梯度下降(stochastic gradient descent)对比:

Mini-Batch 梯度下降算法是介于批量梯度下降算法和随机梯度下降算法之间的算法,每计算常数 次训练实例,便更新一次参数。
在批量梯度下降算法中每次迭代我们都要使用到所有的m个样本,在随机梯度下降中我们每次迭代只需要一个样本。Mini-batch算法具体来说就是每次迭代,会使用b个样本,这个b我们称为mini-batch大小的参数

3. 代码
#coding:utf-8
import random
import math#
# 参数解释:
# "pd_" :偏导的前缀
# "d_" :导数的前缀
# "w_ho" :隐含层到输出层的权重系数索引
# "w_ih" :输入层到隐含层的权重系数的索引class NeuralNetwork:LEARNING_RATE = 0.5def __init__(self, num_inputs, num_hidden, num_outputs, hidden_layer_weights = None, hidden_layer_bias = None, output_layer_weights = None, output_layer_bias = None):self.num_inputs = num_inputsself.hidden_layer = NeuronLayer(num_hidden, hidden_layer_bias)self.output_layer = NeuronLayer(num_outputs, output_layer_bias)self.init_weights_from_inputs_to_hidden_layer_neurons(hidden_layer_weights)self.init_weights_from_hidden_layer_neurons_to_output_layer_neurons(output_layer_weights)def init_weights_from_inputs_to_hidden_layer_neurons(self, hidden_layer_weights):weight_num = 0for h in range(len(self.hidden_layer.neurons)):for i in range(self.num_inputs):if not hidden_layer_weights:self.hidden_layer.neurons[h].weights.append(random.random())else:self.hidden_layer.neurons[h].weights.append(hidden_layer_weights[weight_num])weight_num += 1def init_weights_from_hidden_layer_neurons_to_output_layer_neurons(self, output_layer_weights):weight_num = 0for o in range(len(self.output_layer.neurons)):for h in range(len(self.hidden_layer.neurons)):if not output_layer_weights:self.output_layer.neurons[o].weights.append(random.random())else:self.output_layer.neurons[o].weights.append(output_layer_weights[weight_num])weight_num += 1def inspect(self):print('------')print('* Inputs: {}'.format(self.num_inputs))print('------')print('Hidden Layer')self.hidden_layer.inspect()print('------')print('* Output Layer')self.output_layer.inspect()print('------')def feed_forward(self, inputs):hidden_layer_outputs = self.hidden_layer.feed_forward(inputs)return self.output_layer.feed_forward(hidden_layer_outputs)def train(self, training_inputs, training_outputs):self.feed_forward(training_inputs)# 1. 输出神经元的值pd_errors_wrt_output_neuron_total_net_input = [0] * len(self.output_layer.neurons)for o in range(len(self.output_layer.neurons)):# ∂E/∂zⱼpd_errors_wrt_output_neuron_total_net_input[o] = self.output_layer.neurons[o].calculate_pd_error_wrt_total_net_input(training_outputs[o])# 2. 隐含层神经元的值pd_errors_wrt_hidden_neuron_total_net_input = [0] * len(self.hidden_layer.neurons)for h in range(len(self.hidden_layer.neurons)):# dE/dyⱼ = Σ ∂E/∂zⱼ * ∂z/∂yⱼ = Σ ∂E/∂zⱼ * wᵢⱼd_error_wrt_hidden_neuron_output = 0for o in range(len(self.output_layer.neurons)):d_error_wrt_hidden_neuron_output += pd_errors_wrt_output_neuron_total_net_input[o] * self.output_layer.neurons[o].weights[h]# ∂E/∂zⱼ = dE/dyⱼ * ∂zⱼ/∂pd_errors_wrt_hidden_neuron_total_net_input[h] = d_error_wrt_hidden_neuron_output * self.hidden_layer.neurons[h].calculate_pd_total_net_input_wrt_input()# 3. 更新输出层权重系数for o in range(len(self.output_layer.neurons)):for w_ho in range(len(self.output_layer.neurons[o].weights)):# ∂Eⱼ/∂wᵢⱼ = ∂E/∂zⱼ * ∂zⱼ/∂wᵢⱼpd_error_wrt_weight = pd_errors_wrt_output_neuron_total_net_input[o] * self.output_layer.neurons[o].calculate_pd_total_net_input_wrt_weight(w_ho)# Δw = α * ∂Eⱼ/∂wᵢself.output_layer.neurons[o].weights[w_ho] -= self.LEARNING_RATE * pd_error_wrt_weight# 4. 更新隐含层的权重系数for h in range(len(self.hidden_layer.neurons)):for w_ih in range(len(self.hidden_layer.neurons[h].weights)):# ∂Eⱼ/∂wᵢ = ∂E/∂zⱼ * ∂zⱼ/∂wᵢpd_error_wrt_weight = pd_errors_wrt_hidden_neuron_total_net_input[h] * self.hidden_layer.neurons[h].calculate_pd_total_net_input_wrt_weight(w_ih)# Δw = α * ∂Eⱼ/∂wᵢself.hidden_layer.neurons[h].weights[w_ih] -= self.LEARNING_RATE * pd_error_wrt_weightdef calculate_total_error(self, training_sets):total_error = 0for t in range(len(training_sets)):training_inputs, training_outputs = training_sets[t]self.feed_forward(training_inputs)for o in range(len(training_outputs)):total_error += self.output_layer.neurons[o].calculate_error(training_outputs[o])return total_errorclass NeuronLayer:def __init__(self, num_neurons, bias):# 同一层的神经元共享一个截距项bself.bias = bias if bias else random.random()self.neurons = []for i in range(num_neurons):self.neurons.append(Neuron(self.bias))def inspect(self):print('Neurons:', len(self.neurons))for n in range(len(self.neurons)):print(' Neuron', n)for w in range(len(self.neurons[n].weights)):print(' Weight:', self.neurons[n].weights[w])print(' Bias:', self.bias)def feed_forward(self, inputs):outputs = []for neuron in self.neurons:outputs.append(neuron.calculate_output(inputs))return outputsdef get_outputs(self):outputs = []for neuron in self.neurons:outputs.append(neuron.output)return outputsclass Neuron:def __init__(self, bias):self.bias = biasself.weights = []def calculate_output(self, inputs):self.inputs = inputsself.output = self.squash(self.calculate_total_net_input())return self.outputdef calculate_total_net_input(self):total = 0for i in range(len(self.inputs)):total += self.inputs[i] * self.weights[i]return total + self.bias# 激活函数sigmoiddef squash(self, total_net_input):return 1 / (1 + math.exp(-total_net_input))def calculate_pd_error_wrt_total_net_input(self, target_output):return self.calculate_pd_error_wrt_output(target_output) * self.calculate_pd_total_net_input_wrt_input();# 每一个神经元的误差是由平方差公式计算的def calculate_error(self, target_output):return 0.5 * (target_output - self.output) ** 2def calculate_pd_error_wrt_output(self, target_output):return -(target_output - self.output)def calculate_pd_total_net_input_wrt_input(self):return self.output * (1 - self.output)def calculate_pd_total_net_input_wrt_weight(self, index):return self.inputs[index]# 文中的例子:nn = NeuralNetwork(2, 2, 2, hidden_layer_weights=[0.15, 0.2, 0.25, 0.3], hidden_layer_bias=0.35, output_layer_weights=[0.4, 0.45, 0.5, 0.55], output_layer_bias=0.6)
for i in range(10000):nn.train([0.05, 0.1], [0.01, 0.09])print(i, round(nn.calculate_total_error([[[0.05, 0.1], [0.01, 0.09]]]), 9))#另外一个例子,可以把上面的例子注释掉再运行一下:# training_sets = [
# [[0, 0], [0]],
# [[0, 1], [1]],
# [[1, 0], [1]],
# [[1, 1], [0]]
# ]# nn = NeuralNetwork(len(training_sets[0][0]), 5, len(training_sets[0][1]))
# for i in range(10000):
# training_inputs, training_outputs = random.choice(training_sets)
# nn.train(training_inputs, training_outputs)
# print(i, nn.calculate_total_error(training_sets))三、SOM自组织映射网络
SOM网络又称Kohonen网络,是自组织竞争型神经网络的一种,该网络为无监督学习网络,能够识别环境特征并自动聚类。它通过自动寻找样本中的内在规律和本质属性,自组织、自适应地改变网络参数与结构。
1. SOM网络拓扑结构

- 网络包含两层,即一个输入层和一个输出层,输出层也称竞争层,不包括隐层。
- 输入层中的每个输入节点都与输出节点完全相连。
- 输出节点呈二维结构分布,且节点之间具有侧向连接。于是,对某个输出节点来说,在一定邻域范围内会有一定数量的“邻近细胞”,即邻接节点。
2. 原理
- 分类与输入模式的相似性:分类是在类别知识等导师信号的指导下,将待识别的输入模式分配到各自的模式类中,无导师指导的分类称为聚类,聚类的目的是将相似的模式样本划归一类,而将不相似的分离开来,实现模式样本的类内相似性和类间分离性。由于无导师学习的训练样本中不含期望输出,因此对于某一输入模式样本应属于哪一类并没有任何先验知识。对于一组输入模式,只能根据它们之间的相似程度来分为若干类,因此,相似性是输入模式的聚类依据。
- 相似性测量:神经网络的输入模式向量的相似性测量可用向量之间的距离来衡量。常用的方法有欧氏距离法和余弦法两种。
- 竞争学习原理:竞争学习规则的生理学基础是神经细胞的侧抑制现象:当一个神经细胞兴奋后,会对其周围的神经细胞产生抑制作用。最强的抑制作用是竞争获胜的“唯我独兴”,这种做法称为“胜者为王”(Winner-Take-All)。竞争学习规则就是从神经细胞的侧抑制现象获得的。它的学习步骤为:A、向量归一化;B、寻找获胜神经元;C、网络输出与权调整;D、重新归一化处理。

3. 具体算法
网络学习过程中,当样本输入网络时, 竞争层上的神经元计算 输入样本与 竞争层神经元权值之间的 欧几里德距离,距离最小的神经元为获胜神经元。调整获胜神经元和相邻神经元权值,使获得神经元及周边权值靠近该输入样本。通过反复训练,最终各神经元的连接权值具有一定的分布,该分布把数据之间的相似性组织到代表各类的神经元上,使同类神经元具有相近的权系数,不同类的神经元权系数差别明显。需要注意的是,在学习的过程中,权值修改学习速率和神经元领域均在不断较少,从而使同类神经元逐渐集中。
总的来说,SOM网络包含初始化、竞争、迭代三块内容。
3.1 初始化
- 归一化数据集。
- 设计竞争层结构。一般根据预估的聚类簇数进行设置。比如要分成4类,那我可以将竞争层设计为2*2,1*4,4*1。SOM网络不需要预先提供聚类数量,类别的数据由网络自动识别出来。
- 预设竞争层神经元的权重节点。一般我们会根据输入数据的维度和竞争层预估的分类数来设置权重节点,若输入为二维数据,最终聚类为4类,则权重矩阵就是2*4。
- 初始化邻域半径、学习率。
3.2 竞争过程
- 随机选择样本,根据权重节点计算到竞争层每个神经元节点的距离。一般我们选择欧式距离公式求距离。
(或者另一种方法:权重w和输入x的点积最大判断优胜节点)
- 选择优胜节点。通过竞争,选择距离最小的神经元节点作为优胜节点。
Best Matching Unit(BMU) 优胜节点: The winner node(or weight) which has the shortest distance from itself to the sample vector. There are numerous ways to determine the distance, however, the most commonly used method is the Euclidean Distance, is the most common metric to calculate distance between weights and sample vector.
3.3 迭代过程
1、圈定出优胜邻域(neighborhood)内的所有节点。根据邻域半径,圈定出距离小于邻域半径的节点,形成优胜邻域。
2、对优胜邻域内的节点权重进行迭代更新。更新的思想是越靠近优胜节点,更新幅度越大;越远离优胜节点,更新幅度越小,故我们需要对不同的节点增加一个更新约束,一般可以高斯函数求得。另外我们更新节点的目的是为了使得优胜节点更加逼近样本点,故在节点权重的更新上,我们采用以下公式:

3.4 衰减函数 decay func
SOM网络的另一个特点是,学习率和邻域范围随着迭代次数会逐渐衰减
最常用的decay funciton是 1 / (1 + t/T)
sigma(t) = sigma / (1 + t/T)
learning_rate(t) = learning_rate / (1 + t/T)
t 代表当前迭代次数
T = 总迭代次数 / 2
4. 实际例子
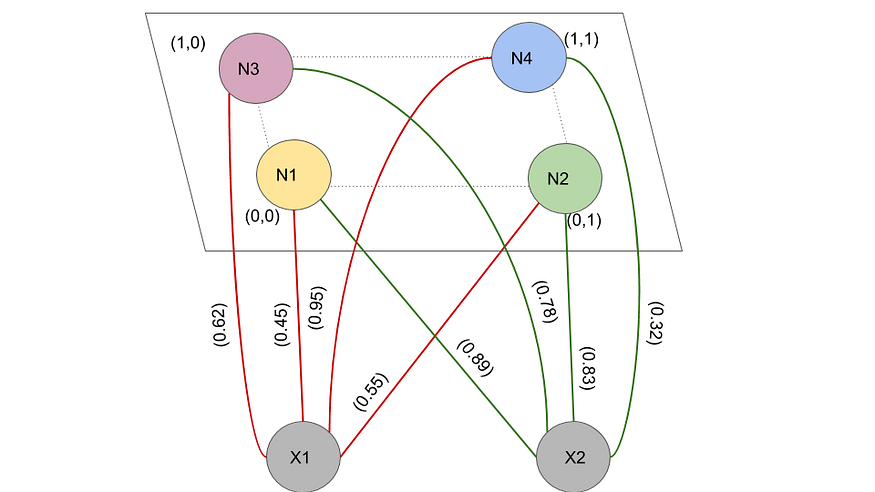
初始权重为w1 = (0.45,0.89) , w2 = (0.55,0.83) , w3 = (0.95,0.32) 和 w4 = (0.62,0.78) 。让四个神经元(N=4),N1, N2, N3和N4分别位于直角坐标平面位置(0,0), (1,0), (1,0)和(1,1)的网格中。假设网络接受二维(A=2)输入矢量(x1,x2)。让w_i= (w1_i,w2_i)为神经元i的权重 . neighborhood radius = 0.6。输入向量X=(3,1)。假设学习率=0.5,并且在整个过程中是恒定的。假设初始权重如图中所述。
5. 代码

References
零基础入门深度学习(1) - 感知器 - 作业部落 Cmd Markdown 编辑阅读器
一文弄懂神经网络中的反向传播法——BackPropagation
Backpropagation
神经网络算法总结_晴晴_Amanda的博客-CSDN博客
批量梯度下降,随机梯度下降,mini-batch随机梯度下降对比说明: - 知乎
机器学习算法推导&手写实现07——SOM网络 - 知乎
自组织映射神经网络(SOM)_意念回复的博客-CSDN博客
https://medium.com/analytics-vidhya/how-does-self-organizing-algorithm-works-f0664af9bf04
相关文章:

神经网络算法入门和代码
文章内容 感知机(Perceptron)反向传播算法(Back Propagation algorithm)RBF(Radial Basis Function,径向基函数) 网络:单一层前馈网络,它使用径向基作为隐层神经元激活函数ART(Adaptive Resona…...

如何用一个端口同时暴露 HTTP1/2、gRPC、Dubbo 协议?
作者:华钟明 本文我们将介绍 Apache Dubbo 灵活的多协议设计原则,基于这一设计,在 Dubbo 框架底层可灵活的选用 HTTP/2、HTTP/REST、TCP、gRPC、JsonRPC、Hessian2 等任一 RPC 通信协议,同时享用统一的 API 与对等的服务治理能力。…...

ToBeWritten之杂项2
也许每个人出生的时候都以为这世界都是为他一个人而存在的,当他发现自己错的时候,他便开始长大 少走了弯路,也就错过了风景,无论如何,感谢经历 转移发布平台通知:将不再在CSDN博客发布新文章,敬…...
Linux三剑客之awk命令详解
1、概述 Linux三剑客:grep、sed、awk。grep主打查找功能,sed主要是编辑行,awk主要是分割列处理。本篇文章我们详细介绍awk命令。 awk其名称得自于它的创始人 Alfred Aho 、Peter Weinberger 和 Brian Kernighan 姓氏的首个字母。awk是一种编…...

C++异常处理:掌握高效、健壮代码的秘密武器
C异常处理全面解析:底层原理、编译器技巧与实用场景C异常机制:让我们迈向更安全、更可靠的代码C异常处理:掌握基本概念什么是异常?异常处理的重要性C异常处理的组成部分:try、catch、throw探索C异常处理的核心…...
Jetpack Compose基础组件之按钮组件
概述 按钮组件Button是用户和系统交互的重要组件之一,它按照Material Design风格实现,我们先看下Button的参数列表,通过参数列表了解下Button的整体功能 Composable fun Button(onClick: () -> Unit, // 点击按钮时的回调modifier: Modi…...
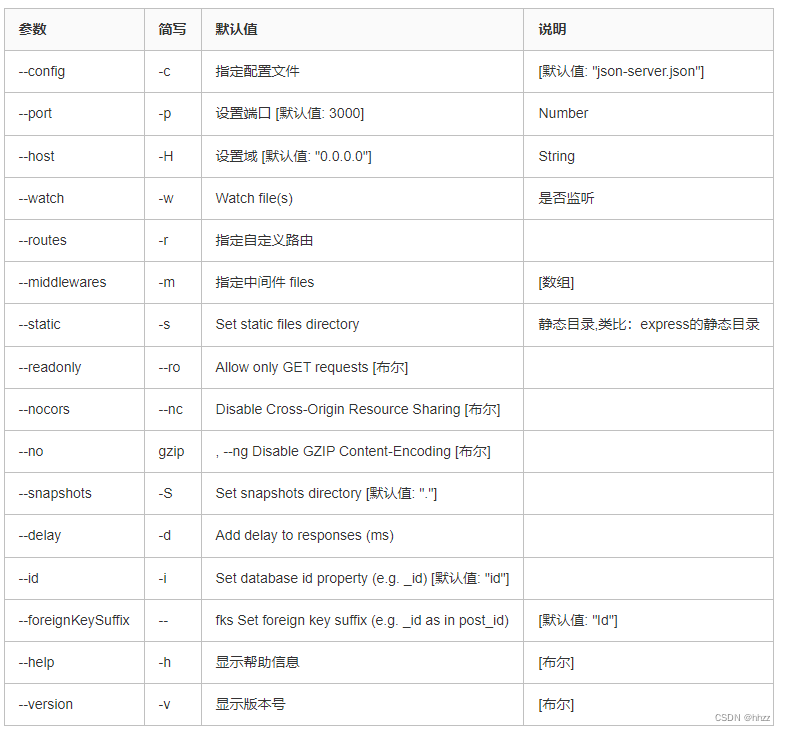
利用json-server快速在本地搭建一个JSON服务
1,json-server介绍 一个在前端本地运行,可以存储json数据的server。 通俗来说,就是模拟服务端接口数据,一般用在前后端分离后,前端人员可以不依赖API开发,而在本地搭建一个JSON服务,自己产生测…...
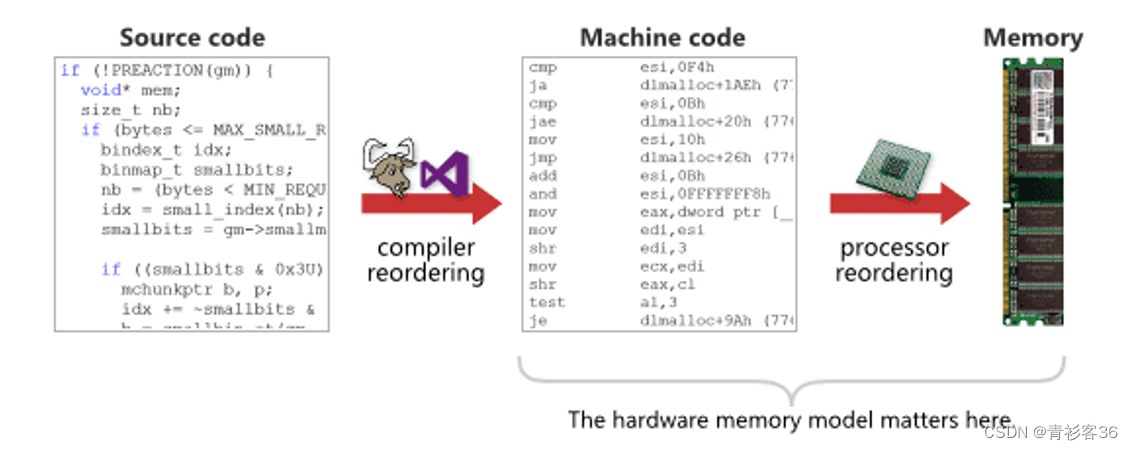
可重入函数与线程安全
指令乱序和线程安全 先来看什么是指令乱序问题以及为什么有指令乱序。程序的代码执行顺序有可能被编译器或CPU根据某种策略打乱指令执行顺序,目的是提升程序的执行性能,让程序的执行尽可能并行,这就是所谓指令乱序问题。理解指令乱序的策略是…...

一文彻底读懂异地多活
文章目录 系统可用性单机架构主从副本风险不可控同城灾备同城双活两地三中心伪异地双活真正的异地双活如何实施异地双活1、按业务类型分片2、直接哈希分片3、按地理位置分片异地多活总结系统可用性 要想理解异地多活,我们需要从架构设计的原则说起。 现如今,我们开发一个软件…...

孕酮PEG偶联物:mPEG Progestrone,PEG Progestrone,甲氧基聚乙二醇孕酮
中文名称:甲氧基聚乙二醇孕酮 英文名称:mPEG Progestrone,PEG Progestrone 一、反应机理: 孕酮-PEG衍生物是一类具有生物活性的类固醇-PEG偶联物,可用于药物发现或生物测定开发。孕酮是一种女性性激素,负…...
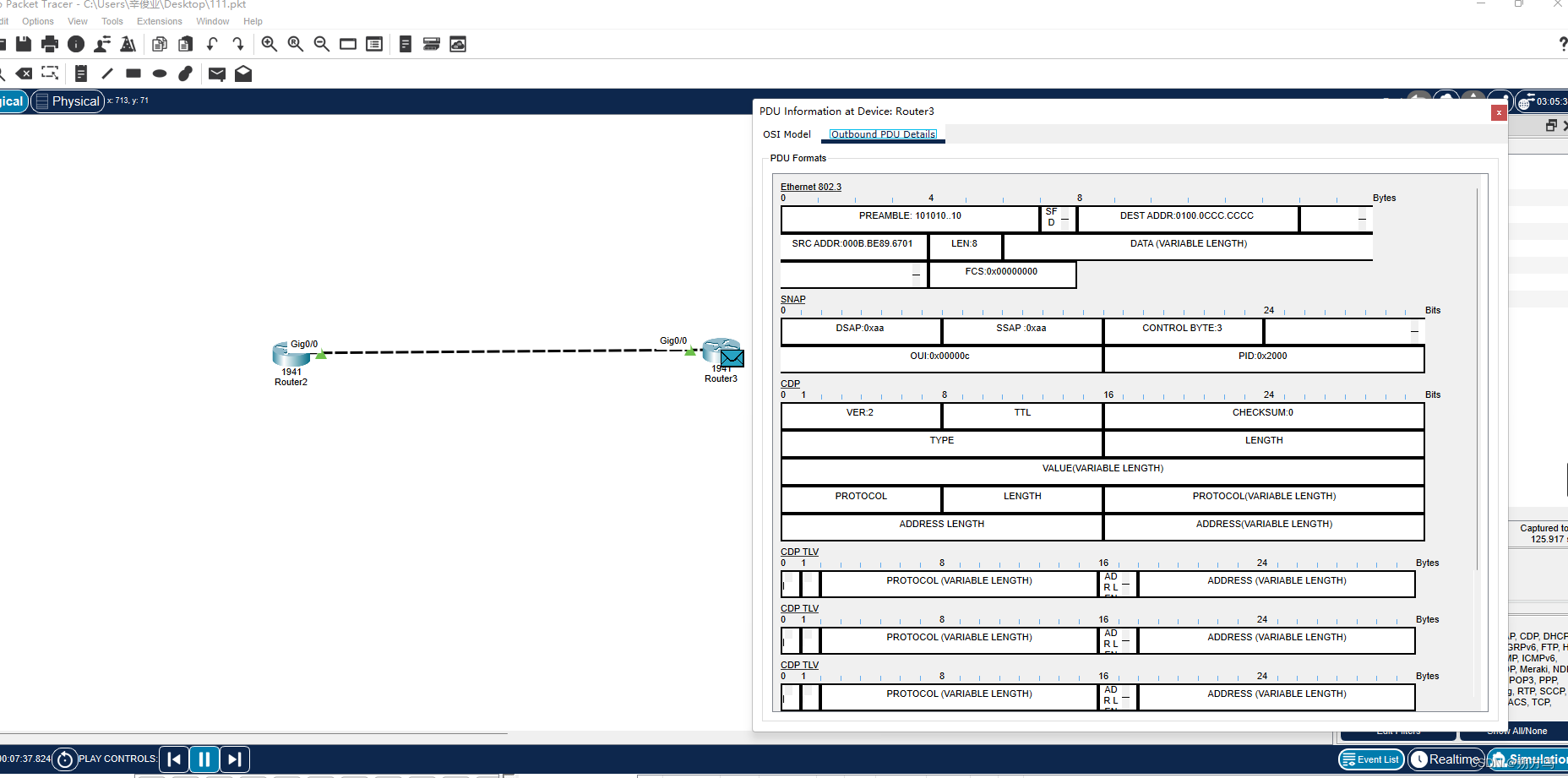
网络系统集成实验(一)| 网络系统集成基础
目录 一、前言 二、实验目的 三、实验需求 四、实验步骤与现象 (1)网络设置、网络命令的使用 ① 在华为设备中,常用指令的使用 ② 在思科设备中,常用指令的使用 ③ 在Windows设备中,常用网络指令的使用 …...
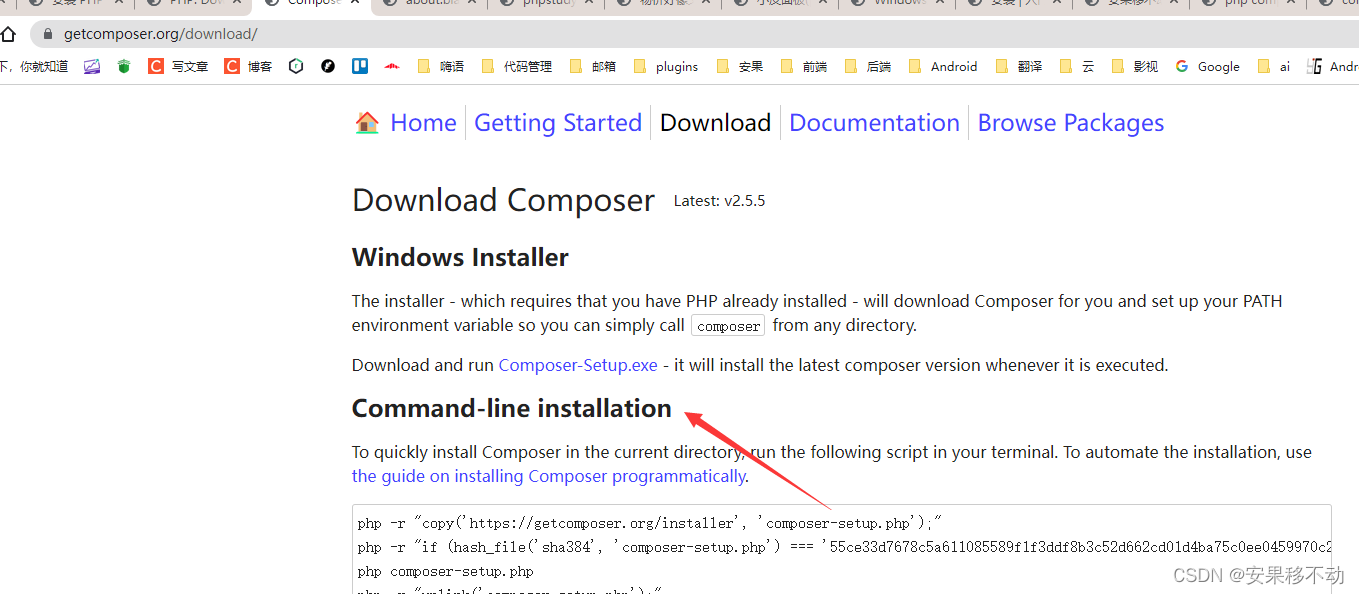
php composer 如何安装windows电脑
在 Windows 电脑上安装 PHP Composer,你需要按照以下步骤操作: 安装 PHP 确保你的电脑上已经安装了 PHP。如果还没有安装,可以从 PHP 官网(https://www.php.net/downloads.php)下载安装包并安装。 设置环境变量 将 P…...
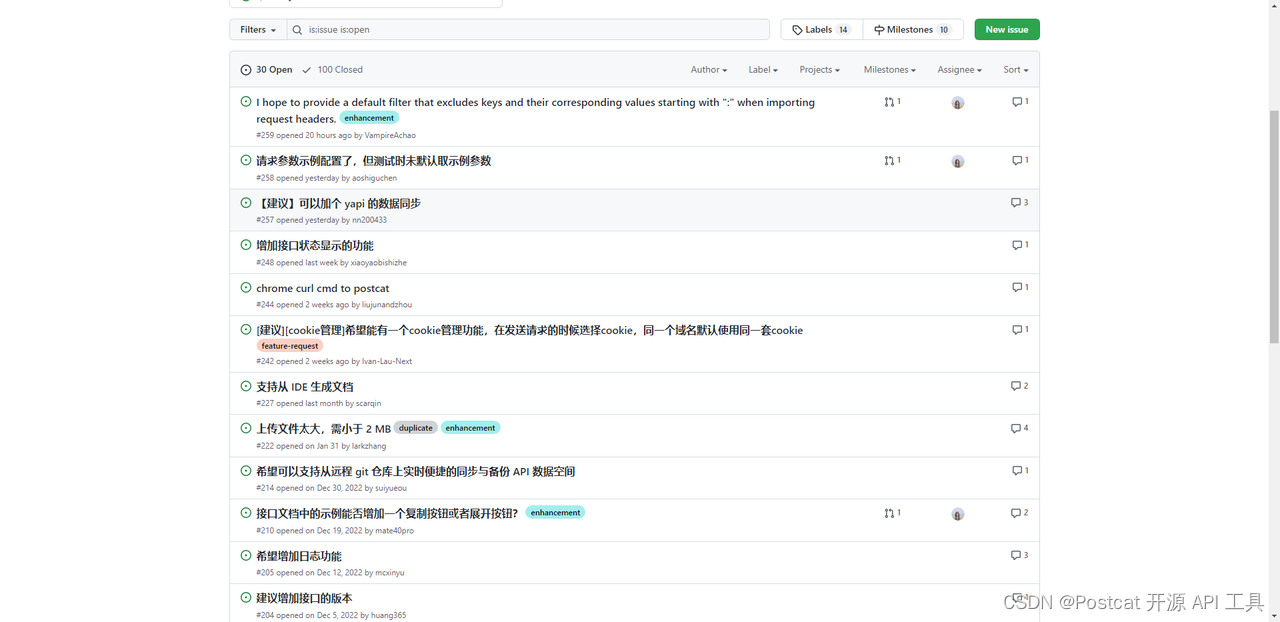
API 鉴权插件上线!支持用户自定义鉴权插件
0.4.0 版本更新主要围绕这几个方面: 分组独立的 UI,支持分组 API 鉴权 API 测试支持继承 API 鉴权 支持用户自定义鉴权插件,仅需部分配置即可发布鉴权插件 开始介绍功能之前,我想先和大家分享一下鉴权功能设计的一些思考。 其实…...
)
2023年NOC大赛加码未来编程赛道-初赛-Python(初中组-卷1)
2023年NOC大赛加码未来编程赛道-初赛-Python(初中组-卷1) *1.Python自带的编程环境是? A、PyScripter B、Spyder C、Notepad++ D、IDLE *2.假设a=20,b-3,那么a or b的结果是? () A、20 B、0 C.1 D.3 *3.假设a=2,b=3,那么a-b*b的值是? A、 3 B、-2 C、-7 D、-11 *4.…...

day21—编程题
文章目录1.第一题1.1题目1.2思路1.3解题2.第二题2.1题目2.2思路2.3解题1.第一题 1.1题目 描述: 洗牌在生活中十分常见,现在需要写一个程序模拟洗牌的过程。 现在需要洗2n张牌,从上到下依次是第1张,第2张,第3张一直到…...

【数据结构】栈与队列经典选择题
🚀write in front🚀 📜所属专栏: 🛰️博客主页:睿睿的博客主页 🛰️代码仓库:🎉VS2022_C语言仓库 🎡您的点赞、关注、收藏、评论,是对我最大的激励…...
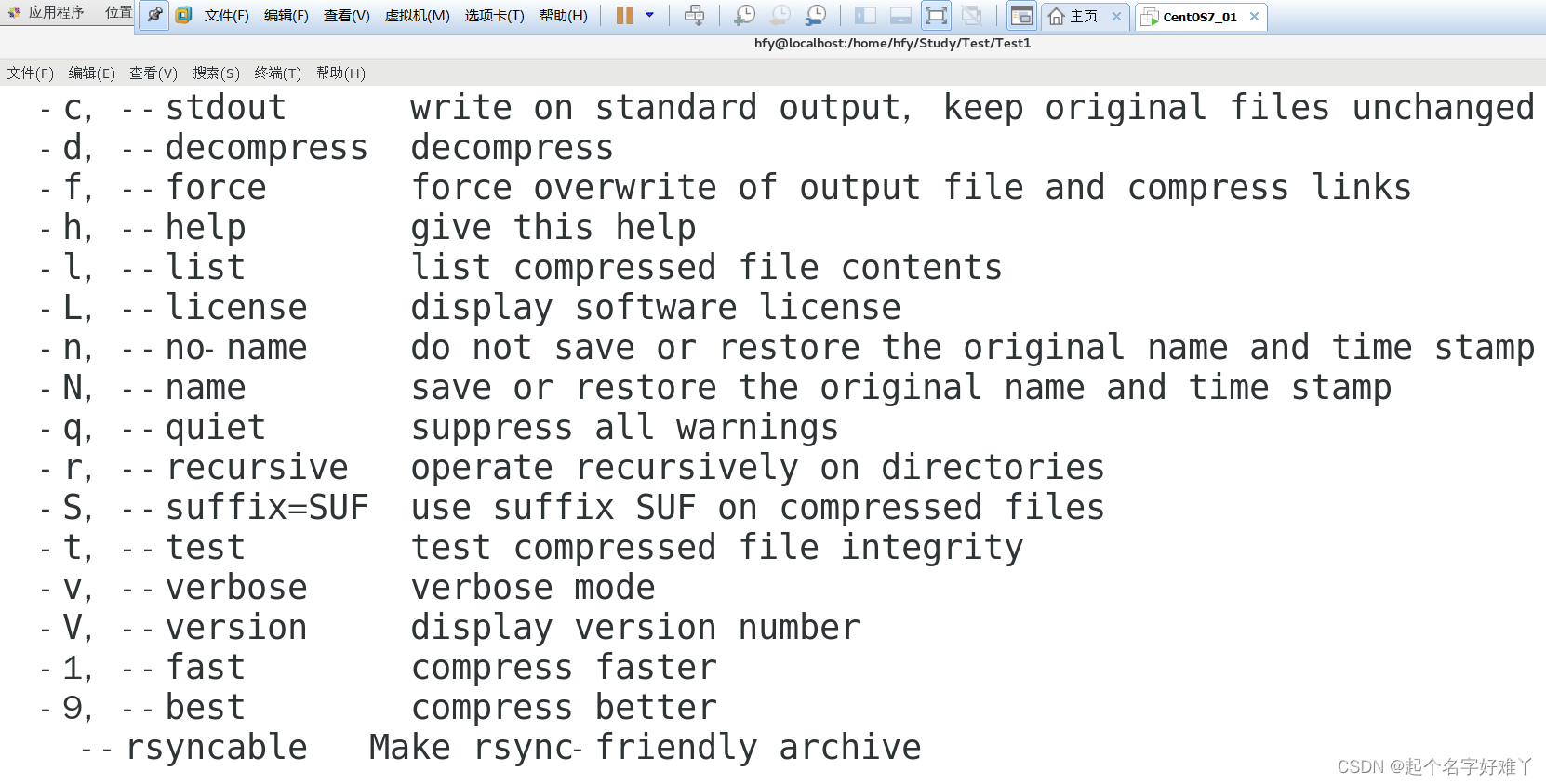
Linux常用命令详细示例演示
一、Linux 常用命令一览表 Linux 下命令格式: command [-options] [parameter] 命令 [选项] [参数] command 是命令 例如:ls cd copy[-options] 带方括号的都是可选的 一些选项 例如:ls -l 中的 -l[parameter] 可选参数,可以是 0…...

9-数据可视化-动态柱状图
文章目录1.基础柱状图2.基础时间线柱状图3.动态柱状图1.基础柱状图 from pyecharts.charts import Bar bar Bar() # 构建柱状图对象 bar.add_xaxis(["中国","美国","英国"]) bar.add_yaxis("GDP",[30,20,10]) bar.render()反转xy轴…...

Linux系统【centos7x】安装宝塔面板教程
1. 下载宝塔面板安装包 在宝塔官网下载最新版的安装包,下载完后上传到服务器。 2. 安装宝塔面板 在终端中输入以下命令: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh…...

蓝易云:Linux系统【Centos7】top命令详细解释
top命令是一个非常常用的Linux系统性能监控工具,它可以实时动态地查看系统的各项性能指标,并且可以按照不同的排序方式进行排序,方便用户查找信息。 下面是top命令的详细解释: 1. 第一行:显示系统的运行时间、当前登…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...
