二叉树_详解
目录
1. 树型结构
1.1 概念
1.2 概念
1.3 树的表示形式
1.4 树的应用
2. 二叉树
2.1 概念
2.2 两种特殊的二叉树
2.3 二叉树的性质
2.4 二叉树的存储
2.5 二叉树的基本操作
2.5.1 前置说明
2.5.2 二叉树的遍历
2.5.3 二叉树的基本操作
1. 树型结构
1.1 概念
- 有一个特殊的结点,称为根结点,根结点没有前驱结点
- 除根结点外,其余结点被分成M(M > 0)个互不相交的集合T1、T2、......、Tm,其中每一个集合Ti (1 <= i <=m) 又是一棵与树类似的子树。每棵子树的根结点有且只有一个前驱,可以有0个或多个后继
- 树是递归定义的。

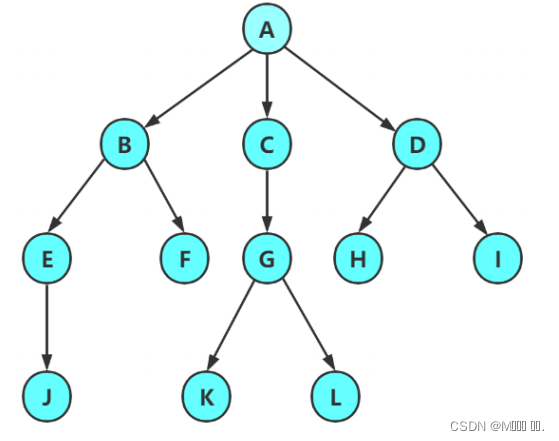
注意:树形结构中,子树之间不能有交集,否则就不是树形结构
1.2 概念
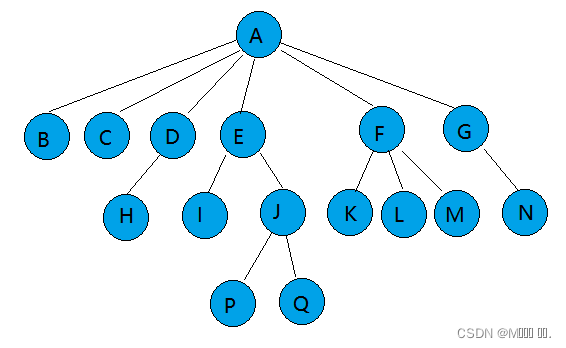
1.3 树的表示形式
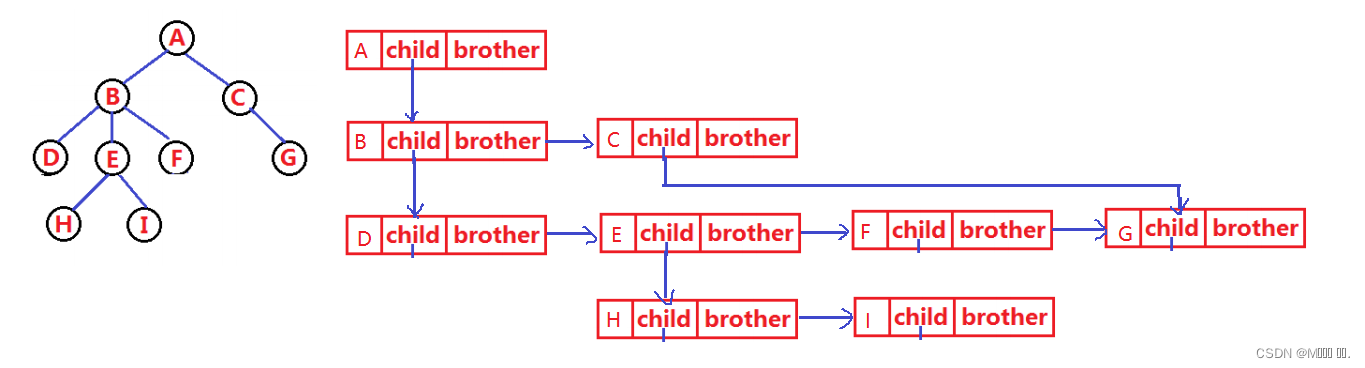
class Node {int value; // 树中存储的数据Node firstChild; // 第一个孩子引用Node nextBrother; // 下一个兄弟引用
}
1.4 树的应用
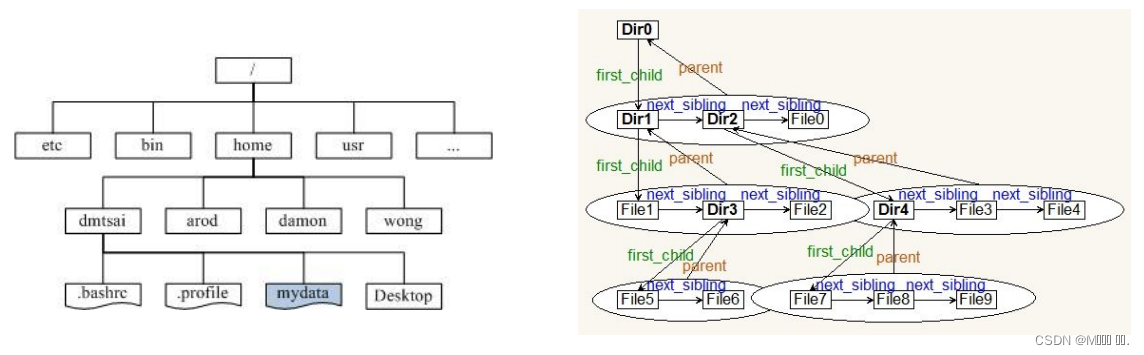
2. 二叉树
2.1 概念
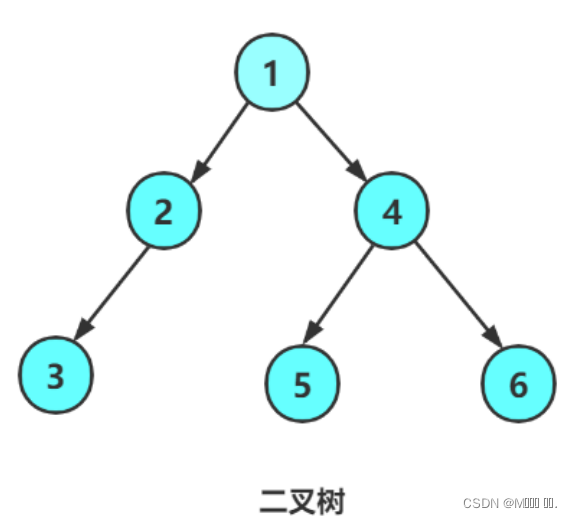
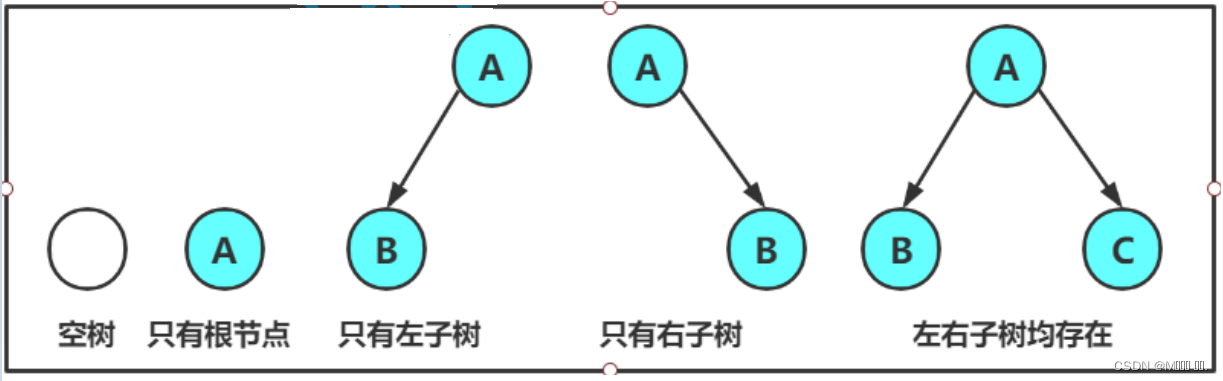
2.2 两种特殊的二叉树
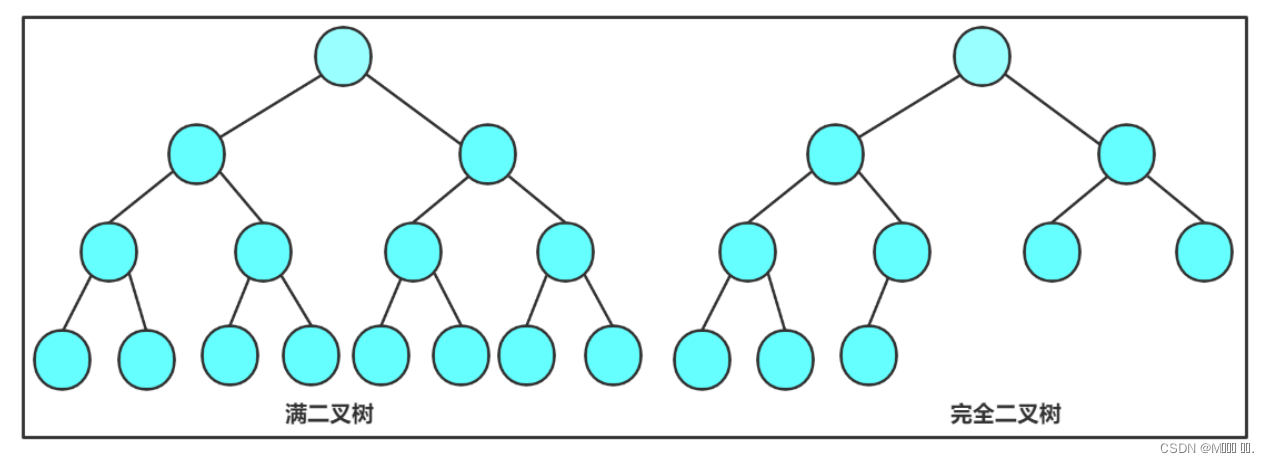
2.3 二叉树的性质
- 若i>0,双亲序号:(i-1)/2;i=0,i为根结点编号,无双亲结点
- 若2i+1<n,左孩子序号:2i+1,否则无左孩子
- 若2i+2<n,右孩子序号:2i+2,否则无右孩子
2.4 二叉树的存储
// 孩子表示法
class Node {int val; // 数据域Node left; // 左孩子的引用,常常代表左孩子为根的整棵左子树Node right; // 右孩子的引用,常常代表右孩子为根的整棵右子树
}
// 孩子双亲表示法
class Node {int val; // 数据域Node left; // 左孩子的引用,常常代表左孩子为根的整棵左子树Node right; // 右孩子的引用,常常代表右孩子为根的整棵右子树Node parent; // 当前节点的根节点
}2.5 二叉树的基本操作
2.5.1 前置说明
public class BinaryTree{public static class BTNode{BTNode left;BTNode right;int value;BTNode(int value){this.value = value;}} private BTNode root;public void createBinaryTree(){BTNode node1 = new BTNode(1);BTNode node1 = new BTNode(2);BTNode node1 = new BTNode(3);BTNode node1 = new BTNode(4);BTNode node1 = new BTNode(5);BTNode node1 = new BTNode(6);root = node1;node1.left = node2;node2.left = node3;node1.right = node4;node4.left = node5;node5.right = node6;}
}2.5.2 二叉树的遍历
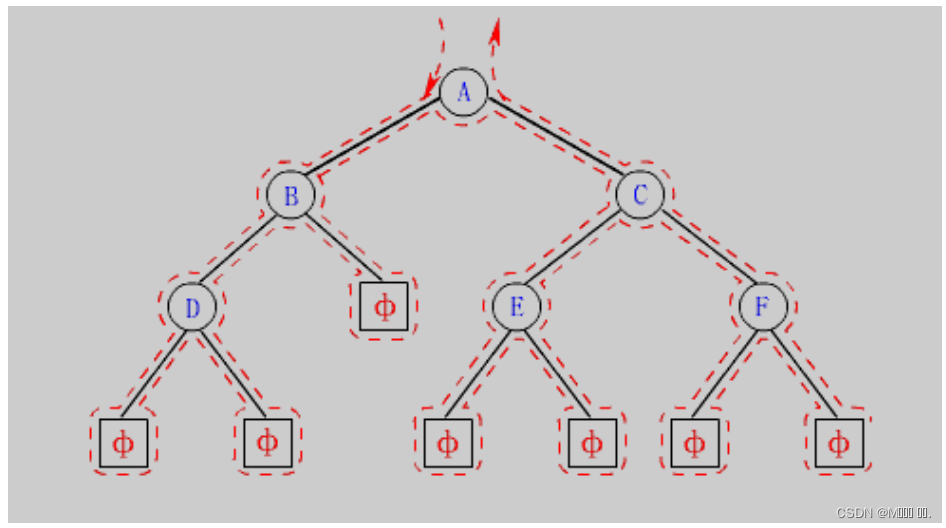
- NLR:前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点--->根的左子树--->根的右子树。
- LNR:中序遍历(Inorder Traversal)——根的左子树--->根节点--->根的右子树。
- LRN:后序遍历(Postorder Traversal)——根的左子树--->根的右子树--->根节点。
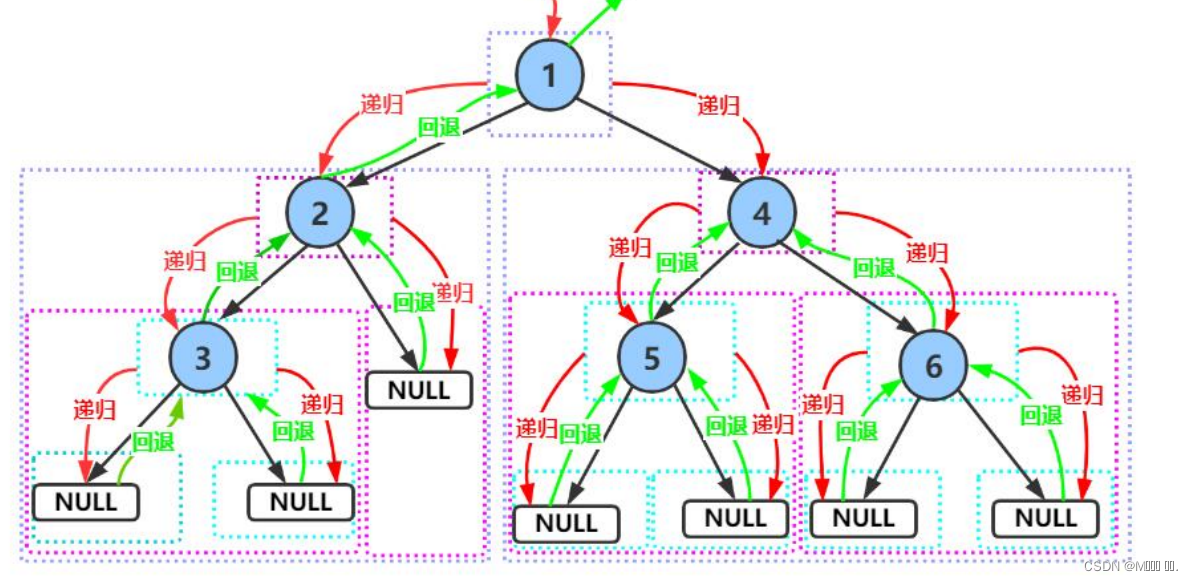
在前几篇文章中我已经写了二叉树的前中后序遍历,这里我就不在写了。
二叉树的前序遍历
二叉树的中序遍历
二叉树的后续遍历
2.5.3 二叉树的基本操作
/*获取叶子节点的个数:遍历思路*/public static int leafSize = 0;int getLeafNodeCount1(TreeNode root) {if (root == null){return 0;}Deque<TreeNode> queue = new LinkedList<>();queue.offer(root);while(!queue.isEmpty()){TreeNode node = queue.poll();if (node.left != null){queue.offer(node.left);}if (node.right != null){queue.offer(node.right);}if (node.left==null && node.right==null){leafSize++;}}return leafSize;}/*获取叶子节点的个数:子问题*/int getLeafNodeCount2(TreeNode root) {if (root == null){return 0;}if (root.right==null && root.left==null){return 1;}return getLeafNodeCount2(root.left)+getLeafNodeCount2(root.right);}/*获取第K层节点的个数*/int getKLevelNodeCount(TreeNode root, int k) {if (root==null || k<=0){return 0;}if (k == 1){return 1;}return getKLevelNodeCount(root.left,k-1)+getKLevelNodeCount(root.right,k-1);}/*获取二叉树的高度时间复杂度:O(N)*/int getHeight(TreeNode root) {if (root == null){return 0;}if (root.left==null && root.right==null){return 1;}return 1+Math.max(getHeight(root.left),getHeight(root.right));}// 检测值为value的元素是否存在Boolean find(TreeNode root, char val) {if (root == null){return false;}if (root.val == val){return true;}return find(root.left,val)||find(root.right,val);}//层序遍历void levelOrder(TreeNode root) {Deque<TreeNode> queue = new LinkedList<>();queue.offer(root);while (!queue.isEmpty()){TreeNode node = queue.poll();System.out.print(node.val + " ");if (node.left != null){queue.offer(node.left);}if (node.right != null){queue.offer(node.right);}}System.out.println();}// 判断一棵树是不是完全二叉树boolean isCompleteTree(TreeNode root) {Deque<TreeNode> queue = new LinkedList<>();queue.offer(root);boolean isStep1 = true;while(!queue.isEmpty()){TreeNode node = queue.poll();if(isStep1){if(node.left!=null && node.right!=null){queue.offer(node.left);queue.offer(node.right);}else if(node.left != null){queue.offer(node.left);isStep1 = false;}else if(node.right != null){return false;}else{isStep1 = false;}}else{if(node.left!=null || node.right!=null){return false;}}}return true;}相关文章:

二叉树_详解
目录 1. 树型结构 1.1 概念 1.2 概念 1.3 树的表示形式 1.4 树的应用 2. 二叉树 2.1 概念 2.2 两种特殊的二叉树 2.3 二叉树的性质 2.4 二叉树的存储 2.5 二叉树的基本操作 2.5.1 前置说明 2.5.2 二叉树的遍历 2.5.3 二叉树的基本操作 1. 树型结构 1.1 概念 …...

LOTO示波器电源环路增益分析客户实测
我们在之前有文章介绍过LOTO示波器信号源扫频测电源环路增益稳定性的方法和过程,可以参考演示视频如下: https://www.ixigua.com/7135738415382790663?logTaga843d537a27090d5117b 或者阅读对应的文章:《LOTO示波器 实测 开环增益频响曲线/电…...
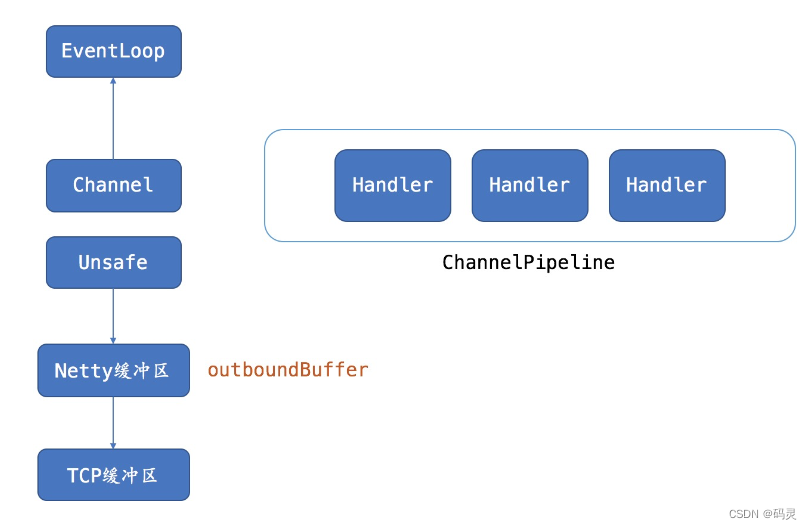
Netty主要组件
: 在Netty中有很多重要的组件, 每个组件职业不同, 担负不同的功能。 组件一 NioEventLoop 在它的底层封装了Selector, 实现多路复用, 由唯一绑定的一个线程去进行三大步骤循环操作: 监听事件,处理事件,执行任务。 组件二 NioServerSocketChannel NioSocketChannel 一个是服务…...

Linux系统【centos7】常用基础命令教程
今天我来介绍一下Linux系统的基础知识。 首先,我们需要了解Linux是什么。Linux是一种免费且开放源代码的操作系统,它被广泛用于服务器、移动设备和嵌入式系统。 接下来,我们需要了解基本的Linux命令。其中一些基本命令包括: 1.…...

【Redis学习】Redis入门概述
Redis是什么 Redis:REmote Dictionary Server(远程字典服务器) 官网介绍:The open source, in-memory data store used by millions of developers as a database, cache, streaming engine, and message broker.(被数百万开发人员用作数据库、缓存、流…...
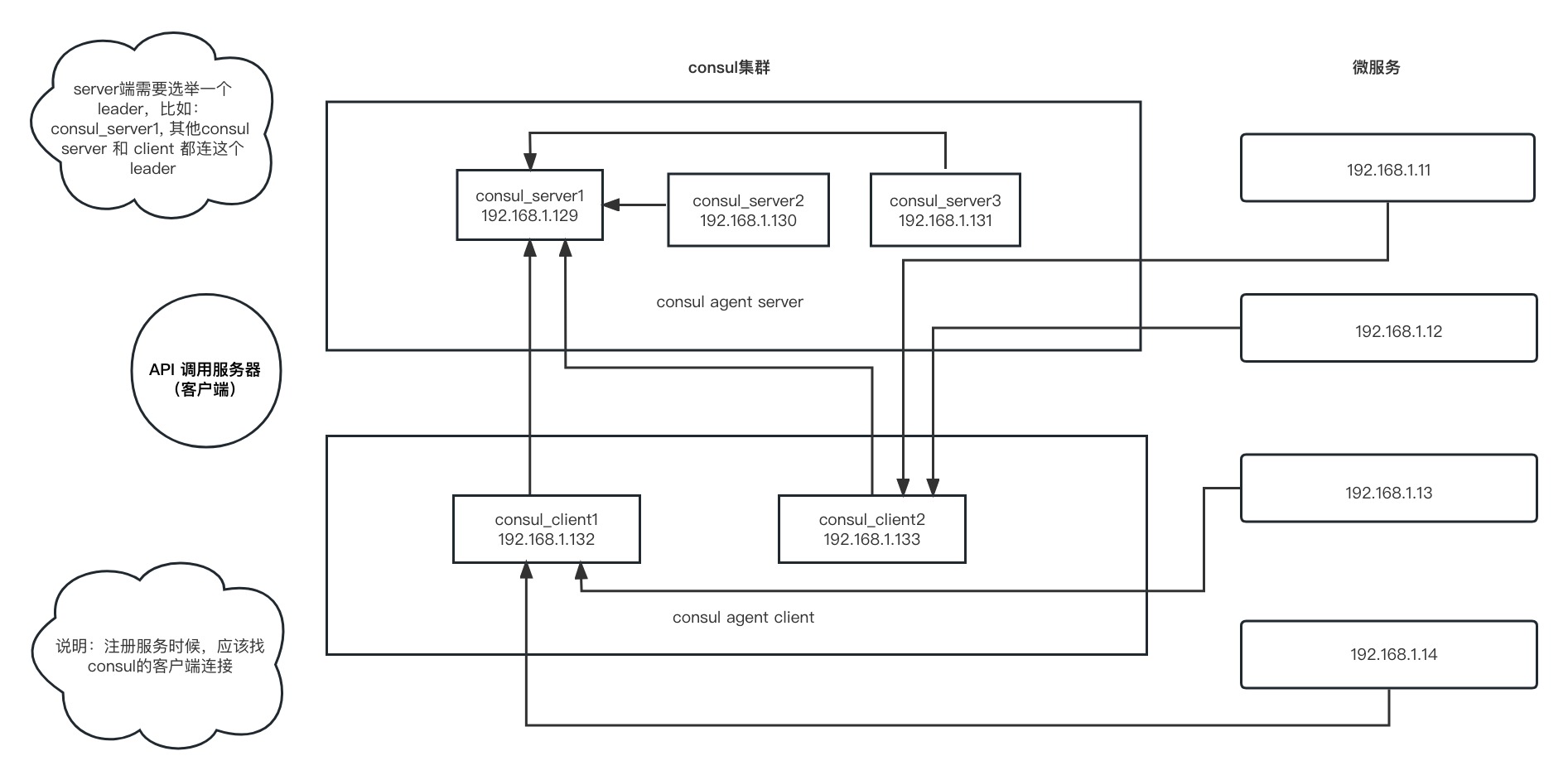
nodejs微服务:Consul集群
Consule集群 1 )概述 Consul是HashiCorp 公司推出的开源工具,用于实现分布式系统的服务发现与配置Consul是分布式的、高可用的、可横向扩展的, 完成consul的安装后,必须运行agentagent可以运行为 server模式、client模式, 每个数据中心至少…...
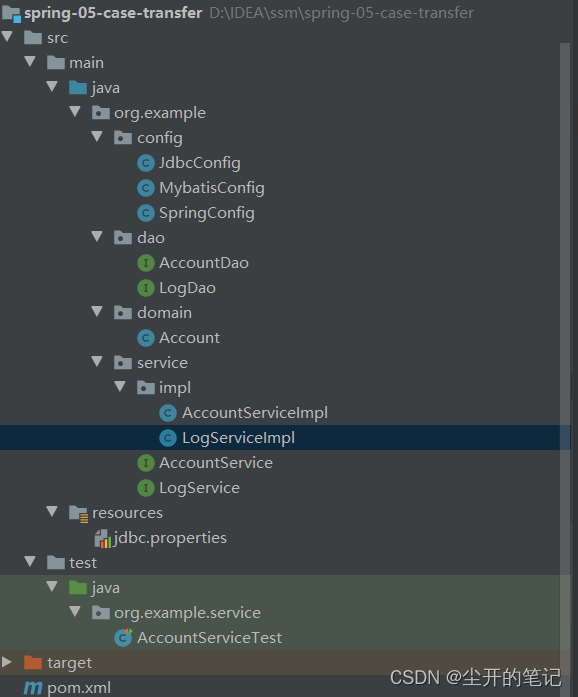
spring事务处理
系列文章目录 Spring中事务的处理相关内容的学习 文章目录系列文章目录前言一、Spring事务简介二、案例:银行账户转账1.题目要求和思路分析2.实现步骤3.实现结构三、spring事务角色四、spring事务相关配置五、案例:转账业务追加日志1.题目要求和思路分析…...

2023 年博客之星的入围规则
目的 感谢各位博主和社区的大力支持,我们的博客之星活动成为了 IT界非常知名的博主荣誉的象征,博主在这个过程中也给大家贡献了很多优质内容。 在过去的几年中,博主们给我们博客之星活动提了很多建议,其中最强烈的一点就是&#…...

【新2023Q2押题JAVA】华为OD机试 - 查找树中的元素 or 查找二叉树节点
最近更新的博客 华为od 2023 | 什么是华为od,od 薪资待遇,od机试题清单华为OD机试真题大全,用 Python 解华为机试题 | 机试宝典【华为OD机试】全流程解析+经验分享,题型分享,防作弊指南华为od机试,独家整理 已参加机试人员的实战技巧本篇题解:查找树中的元素 or 查找二叉树…...

MySQL 日志:undo log、redo log、binlog 有什么用?
目录一、bin log1.作用2.刷盘时机3.日志格式二、redo log1.为什么需要redo log2.基本概念3.作用3.刷盘时机三、undo log1.作用四、Mysql的时机顺序五、redo log 与 binlog 的两阶段提交六、总结一、bin log 1.作用 MySQL的bin log日志是用来记录MySQL中增删改时的记录日志。 …...
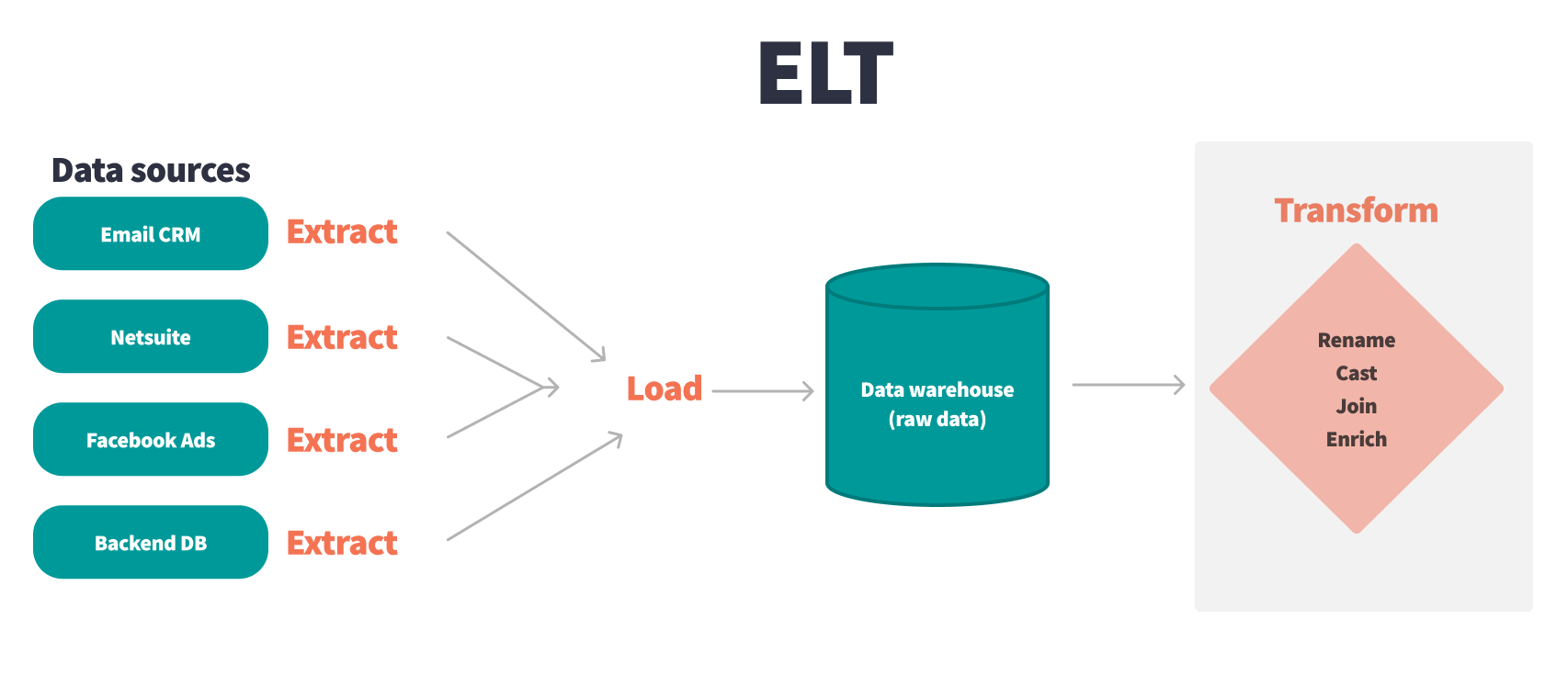
ETL 与 ELT的关键区别
ETL 和 ELT 之间的主要区别在于数据转换发生的时间和地点 — 这些变化可能看起来很小,但会产生很大的影响! ETL 和 ELT 是数据团队引入、转换并最终向利益干系人公开数据的两种主要方式。它们是与现代云数据仓库和 ETL 工具的开发并行发展的流程。 在任…...

Thinkphp 6.0模版的杂项和表单令牌
本节课我们来学习一下模版的杂项和表单令牌的功能。 一.模版的杂项 1. 有时,我们需要输出类似模版标签或语法的数据,这时会被模版解析; 2. 此时,我们就使用模版的原样输出标签{literal}; {literal} 变量标…...

linux常问
查看当前进程 ps -l 列出与本次登录有关的进程信息; ps -aux 查询内存中进程信息; ps -aux | grep * 查询 *进程的详细信息; top 查看内存中进程的动态信息; kill -9 pid 杀死进程。...

ToBeWritten之物联网MQTT、Z-Wave等协议
也许每个人出生的时候都以为这世界都是为他一个人而存在的,当他发现自己错的时候,他便开始长大 少走了弯路,也就错过了风景,无论如何,感谢经历 转移发布平台通知:将不再在CSDN博客发布新文章,敬…...
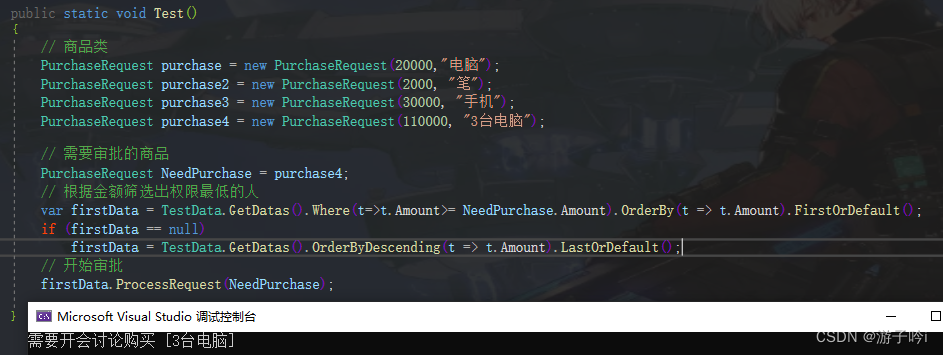
C# 行为型模式之责任链模式
责任链模式:请求从链中的一个对象传递到下一个对象,直到请求被响应为止。通过这种方式在对象之间去除耦合。 用途:请假审批、采购审批等。 案例介绍:以公司采购东西为例子来实现责任链模式。公司规定,采购架构总价在…...

layui实现请求前添加一个加载 loading 的效果,并在请求成功后关闭
1.使用 layui 的 layer 组件来实现请求前添加一个加载 loading 的效果,并在请求成功后关闭。 $("#switch").click(function() {layer.confirm(确认切换至英文环境?, function(index) {var loadingIndex layer.load(1, {shade: [0.1,#fff] //0.1透明度的…...

iostat / sar 命令详解
作用 iostat主要用于监控系统设备的IO负载情况,根据这个可以看出当前系统的写入量和读取量,CPU负载和磁盘负载。 iostat属于sysstat软件包。可以用yum install sysstat 直接安装。 iostat用法 1.用法:iostat [选项] [<时间间隔>] […...
2023-04-06:拥抱Golang,优化FFmpeg音频编码器,探究encode_audio.c的内部结构。
2023-04-06:拥抱Golang,优化FFmpeg音频编码器,探究encode_audio.c的内部结构。 答案2023-04-06: 见moonfdd/ffmpeg-go库。 这段代码是一个示例程序,用于将音频 PCM 数据编码为 MP2 格式的音频文件。下面是代码的详细…...
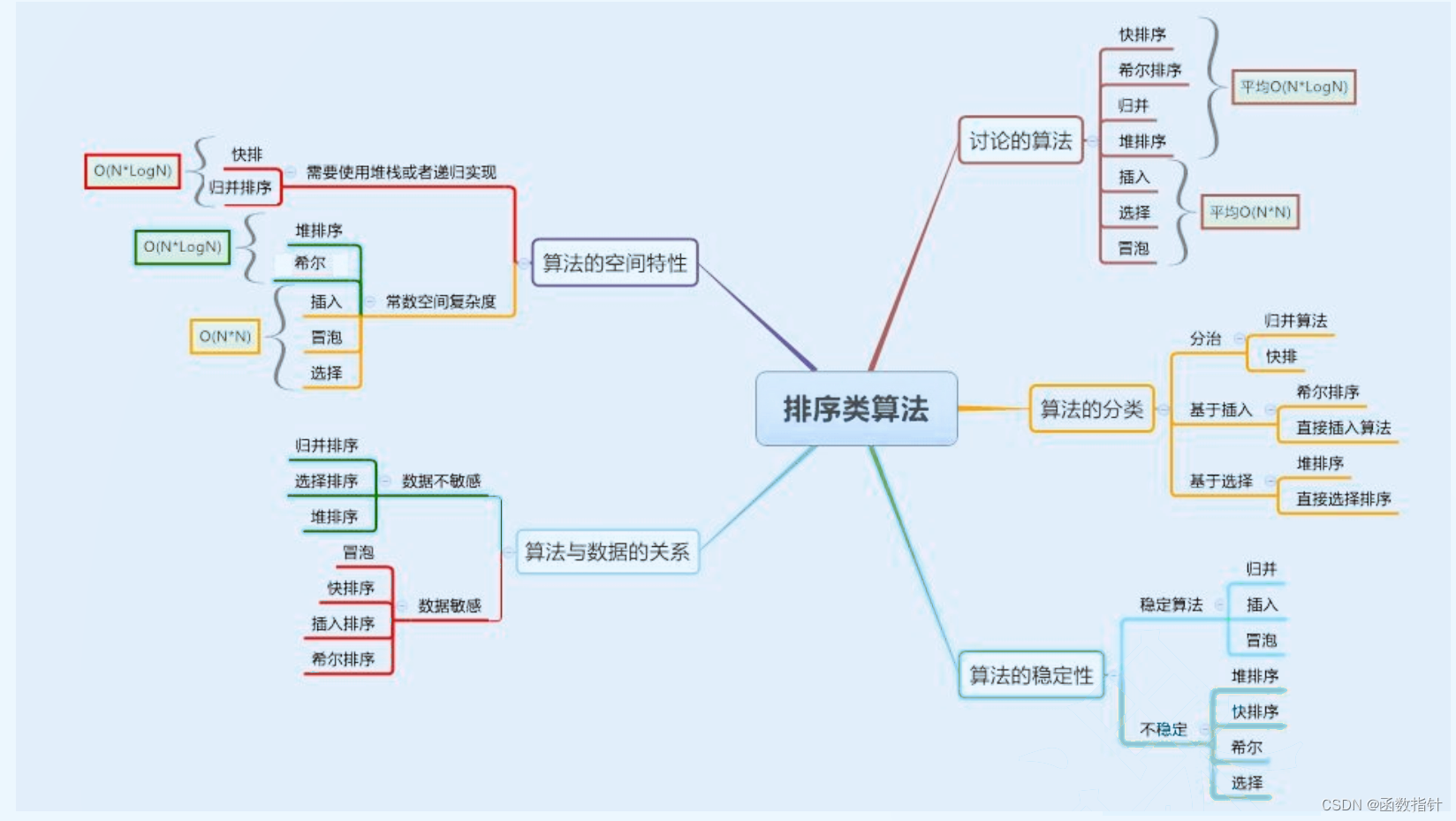
归排、计排深度理解
归并排序:是创建在归并操作上的一种有效的排序算法。算法是采用分治法(Divide and Conquer)的一个非常典型的应用,且各层分治递归可以同时进行。归并排序思路简单,速度仅次于快速排序,为稳定排序算法&#…...
)
设计原则(单一职责原则 开放封闭原则 里氏替换原则 依赖倒置原则 接口隔离原则 迪米特法则)
设计原则单一职责原则(SRP)从三大特性角度看原则:应用的设计模式:开放封闭原则(OCP)从三大特性角度看原则:应用的设计模式:里氏替换原则(LSP)从三大特性角度看原则:应用的设计模式:依赖倒置原则(DIP)从三大特性角度看原则:应用的设计模式&…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...
