归排、计排深度理解
归并排序:是创建在归并操作上的一种有效的排序算法。算法是采用分治法(Divide and Conquer)的一个非常典型的应用,且各层分治递归可以同时进行。归并排序思路简单,速度仅次于快速排序,为稳定排序算法,一般用于对总体无序,但是各子项相对有序的数列。
1. 基本思想
归并排序是用分治思想,分治模式在每一层递归上有三个步骤:
- 分解(Divide):将n个元素分成个含n/2个元素的子序列。
- 解决(Conquer):用合并排序法对两个子序列递归的排序。
- 合并(Combine):合并两个已排序的子序列已得到排序结果。
归并排序的特性总结:
1. 归并的缺点在于需要O(N)的空间复杂度,归并排序的思考更多的是解决在磁盘中的外排序题。
2. 时间复杂度:O(N*logN)
3. 空间复杂度:O(N)
4. 稳定性:稳定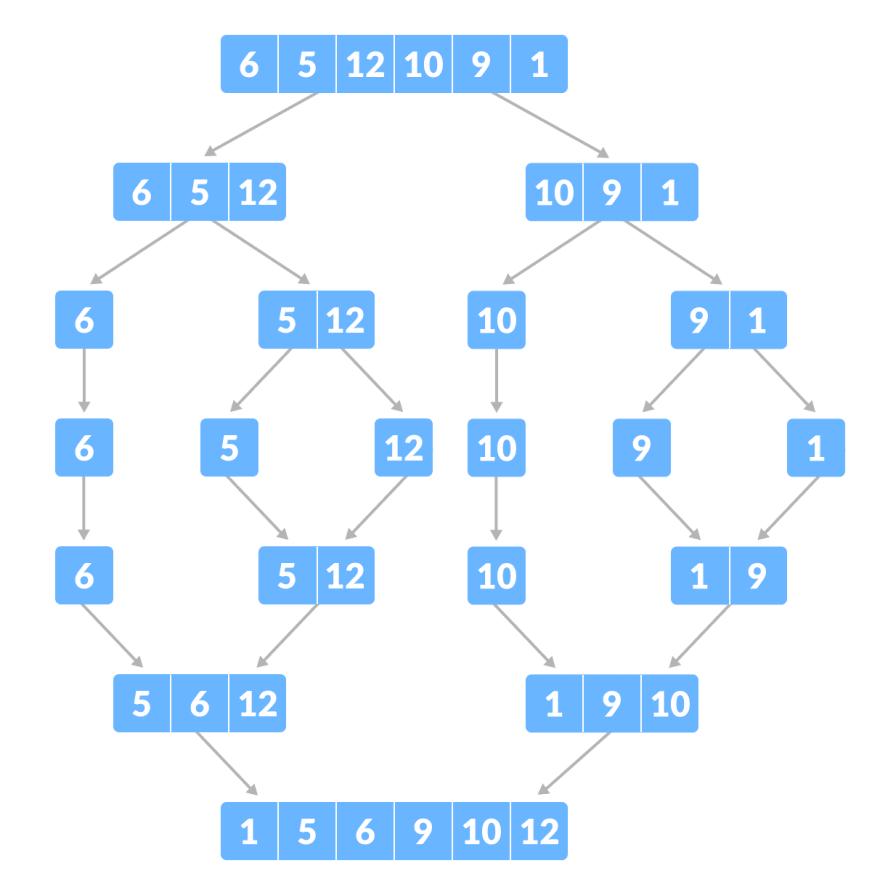
这是归并排序的主要概念。
归并排序有递归和非递归两种,我们首先来实现递归的代码
代码
//归并递归
void _MergeSore(int* arr, int left, int right, int* tmp)
{//递归结束条件if (left >= right)return;//int min = left + ((right - left) >> 1);int min = (left + right) / 2;//递归开始_MergeSore(arr, left, min, tmp);_MergeSore(arr, min + 1, right, tmp);//排序开始int begin1 = left, end1 = min;int begin2 = min + 1, end2 = right;int i = left;while (begin1 <= end1 && begin2 <= end2){if (arr[begin1] < arr[begin2]){tmp[i++] = arr[begin1++];/*i++;begin1++;*/}if (arr[begin1] >= arr[begin2]){tmp[i++] = arr[begin2++];/*i++;begin2++;*/}}while (begin1 <= end1){tmp[i++] = arr[begin1++];}while (begin2 <= end2){tmp[i++] = arr[begin2++];}//将建立的数组拷贝到原数组中for (int i = 0; i <= right; i++){arr[i] = tmp[i];}
}
//归并排序
void MergeSort(int* arr, int n)
{//先建立一个数组,用来存放排序的元素int* tmp = (int*)malloc(sizeof(int) * (n));if (tmp == NULL){perror("perror,file");return;}//归并函数实现_MergeSore(arr, 0, n - 1, tmp);//销毁新建数组,防止内存泄漏free(tmp);//防止野指针tmp = NULL;
}下面是非递归的写法,非递归的思想与递归的思想几乎一样,大家可以自己想下过程。
- 申请空间,使其大小为两个已经排序序列之和,该空间用来存放合并后的序列
- 设定两个指针,最初位置分别为两个已经排序序列的起始位置
- 比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置
- 重复步骤③直到某一指针到达序列尾
- 将另一序列剩下的所有元素直接复制到合并序列尾
void _MergeSoreNonR1(int* arr, int left, int right, int* tmp)
{int gap = 1;int i = 0;while (gap <= right){for (i = 0; i <= right; i += 2 * gap){//[i,I+gap-1] [i+gap,2*gap-1]int begin1 = i, end1 = i + gap - 1;int begin2 = i + gap, end2 = i + 2 * gap - 1;//printf(" %d", end2);if (end1 > right)end1 = right;if (begin2 > right){begin2 = right + 1;end2 = right;}if (end2 > right)end2 = right;int index = i;while (begin1 <= end1 && begin2 <= end2){if (arr[begin1] < arr[begin2]){tmp[index++] = arr[begin1++];}if (arr[begin1] >= arr[begin2]){tmp[index++] = arr[begin2++];}}while (begin1 <= end1){tmp[index++] = arr[begin1++];}while (begin2 <= end2){tmp[index++] = arr[begin2++];}}for (i = 0; i <= right; i++){arr[i] = tmp[i];}gap *= 2;}
}void MergeSortNonR(int* arr, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc,file");return;}_MergeSoreNonR1(arr, 0, n-1, tmp);free(tmp);tmp = NULL;
}下面来看计数排序
计数排序不用比较两个数的大小,它的做法是统计哪个元素出现的次数,然后通过这个元素出现的次数来排序。
计数算法只能使用在已知序列中的元素在0-k之间,且要求排序的复杂度在线性效率上。 Â 计数排序和基数排序很类似,都是非比较型排序算法。但是,它们的核心思想是不同的,基数排序主要是按照进制位对整数进行依次排序,而计数排序主要侧重于对有限范围内对象的统计。基数排序可以采用计数排序来实现。
计数排序的特性总结:
1. 计数排序在数据范围集中时,效率很高,但是适用范围及场景有限。
2. 时间复杂度:O(MAX(N,范围))
3. 空间复杂度:O(范围)
4. 稳定性:稳定
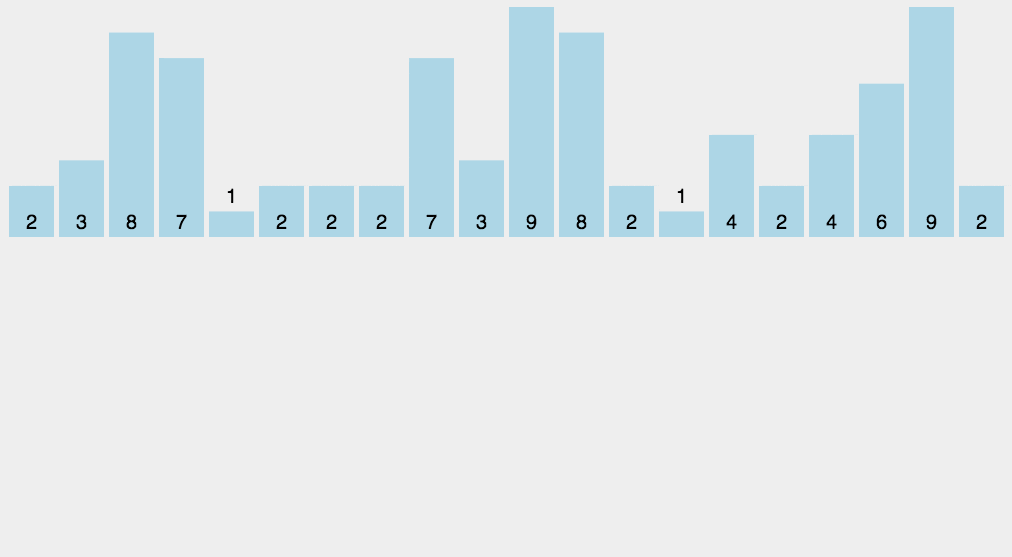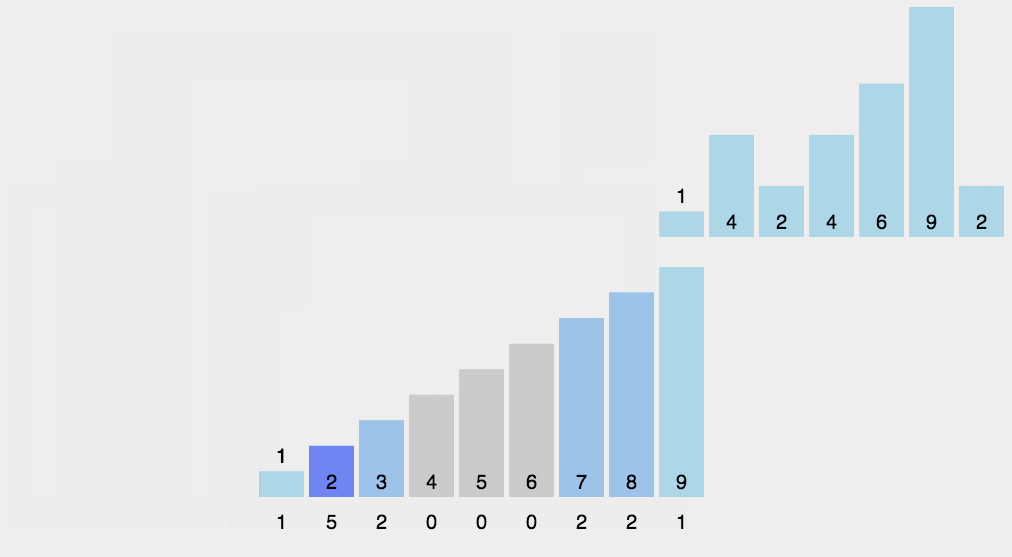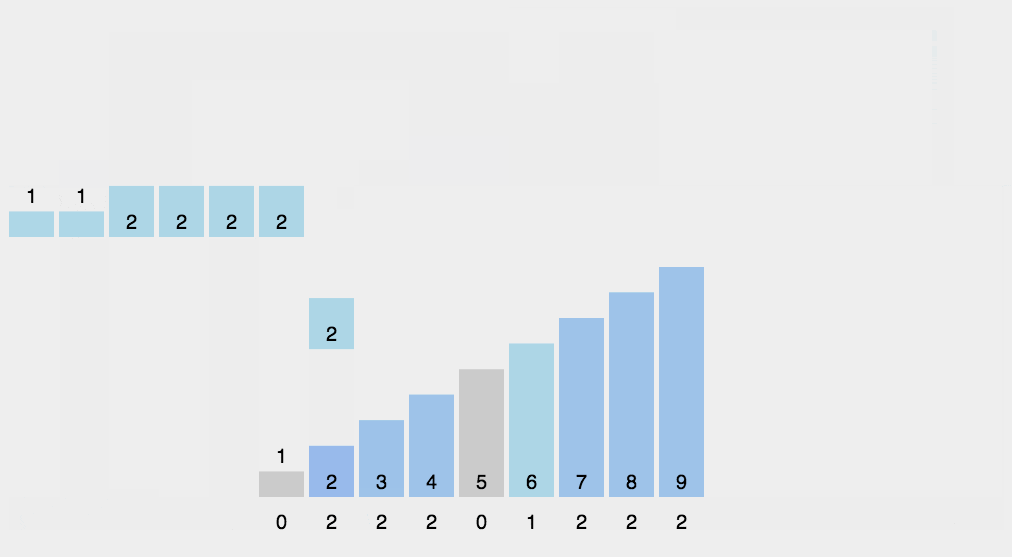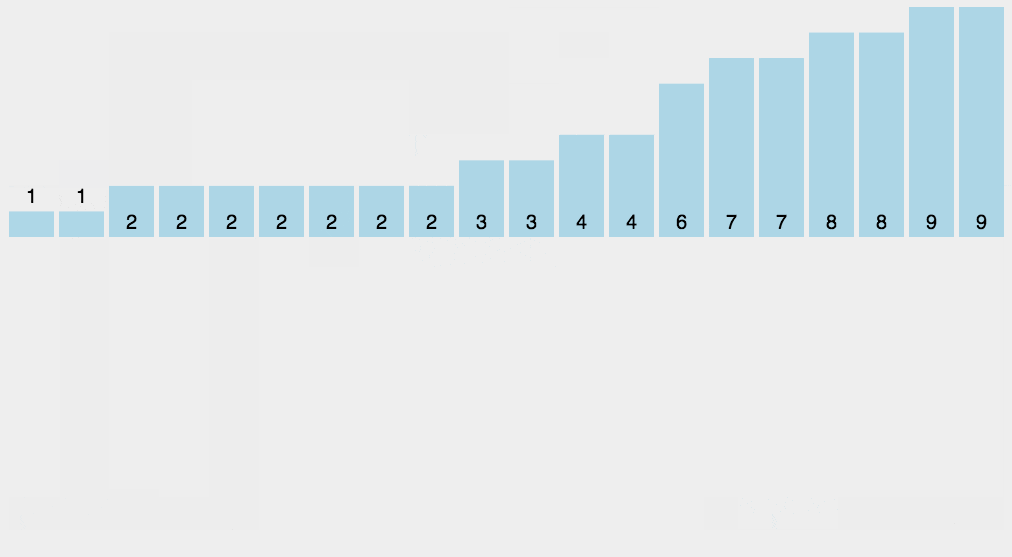
代码实现
void CountSort(int* arr, int n)
{//确定数组开辟的大小int max = arr[0], min = arr[0];for (int i = 1; i < n; i++){if (arr[i] > max)max = arr[i];if (arr[i] < min)min = arr[i];}int range = max - min + 1;//建立一个数组int* count = (int*)malloc(sizeof(int) * range);if (count == NULL){perror("malloc file");return NULL;}memset(count, 0, sizeof(int) * range);for (int i = 0; i < n; i++){count[arr[i]-min]++;}int j = 0;for (int i = 0; i < n; i++){while (count[i]--){arr[j] = i+min;j++;}}free(count);count = NULL;
}下面是一张八大排序的比较图
相关文章:

归排、计排深度理解
归并排序:是创建在归并操作上的一种有效的排序算法。算法是采用分治法(Divide and Conquer)的一个非常典型的应用,且各层分治递归可以同时进行。归并排序思路简单,速度仅次于快速排序,为稳定排序算法&#…...
)
设计原则(单一职责原则 开放封闭原则 里氏替换原则 依赖倒置原则 接口隔离原则 迪米特法则)
设计原则单一职责原则(SRP)从三大特性角度看原则:应用的设计模式:开放封闭原则(OCP)从三大特性角度看原则:应用的设计模式:里氏替换原则(LSP)从三大特性角度看原则:应用的设计模式:依赖倒置原则(DIP)从三大特性角度看原则:应用的设计模式&…...

好像模拟了一个引力场
( A, B )---3*30*2---( 1, 0 )( 0, 1 ) 做一个网络让输入只有3个节点,每个训练集里有4张图片,让B的训练集全为0,排列组合A,观察迭代次数平均值的变化。 A-B 迭代次数 0 1 0 2*0*0*7-0*0*0*0 12957.31 0 0 0 2*0*0*7-0*0…...
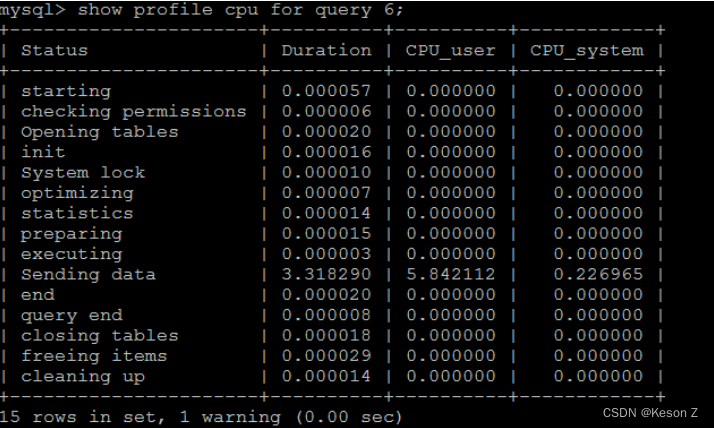
MySQL优化——Explain分析执行计划详解
文章目录前言一. 查看SQL执行频率二. 定位低效率执行SQL三. explain分析执行计划3.1 id3.2 select_type3.3 table3.4 type3.5 key3.6 rows3.7 extra四. show profile分析SQL前言 在应用的的开发过程中,由于初期数据量小,开发人员写 SQL 语句时更重视功能…...

xcode 14.3 file not found libarclite_iphoneos.a
最近升级到xcode 14.3 版本的同学,会遇到这个一个问题 File not found: /Users/johnson/Downloads/Xcode-beta.app/Contents/Developer/Toolchains/XcodeDefault.xctoolchain/usr/lib/arc/libarclite_iphoneos.a 解决方法(亲测有效) 在podfile文件中,增…...
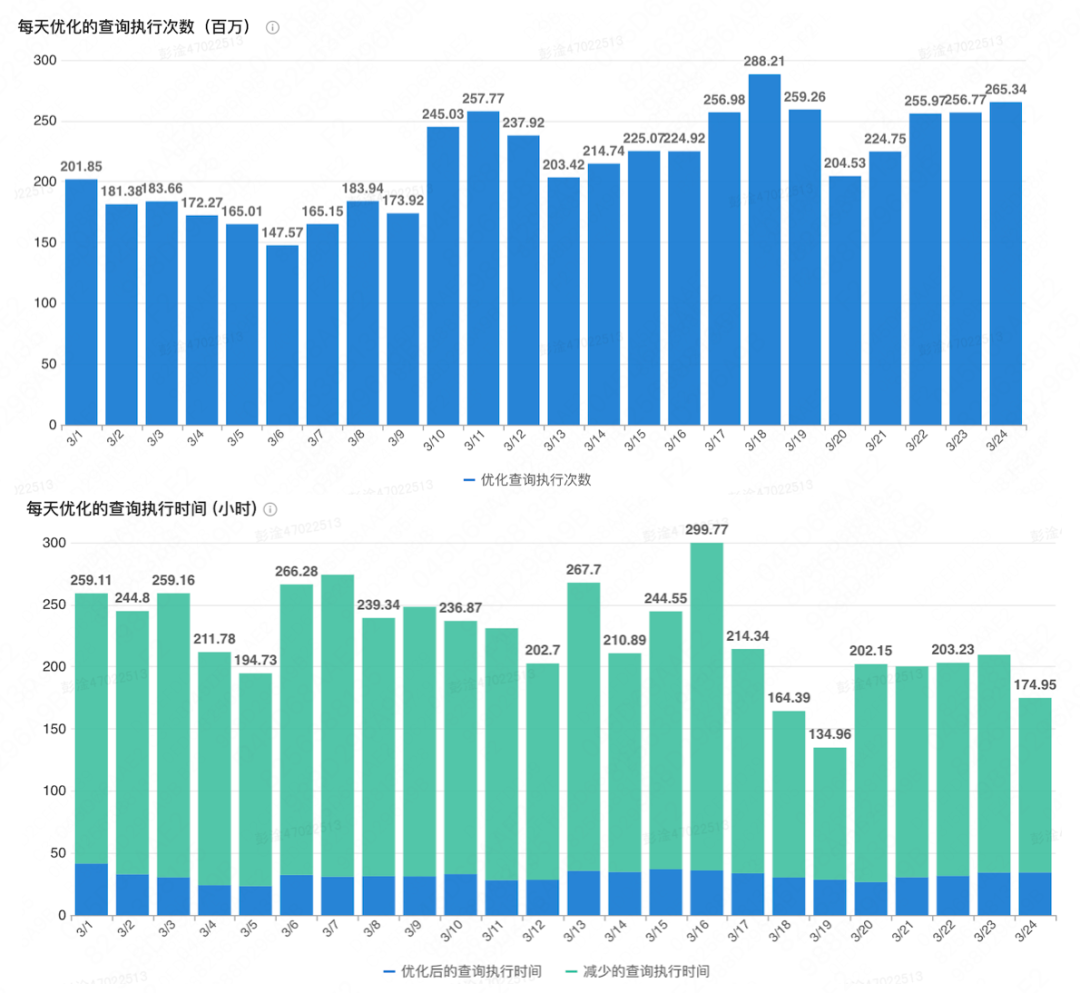
基于AI+数据驱动的慢查询索引推荐
目前,美团内部每天产生的慢查询数量已经超过上亿条。如何高效准确地为慢查询推荐缺失的索引来改善其执行性能,是美团数据库研发中心面临的一项挑战。为此,我们与华东师范大学开展了科研合作,在AI领域对索引推荐进行了探索和实践&a…...

【ESP32】嵌入式FreeRtos--Task
FreeRTOS中文数据手册:https://www.freertos.org/zh-cn-cmn-s/RTOS.html 任务函数 任务函数描述xTaskCreate()使用动态的方法创建一个任务xTaskCreateStatic()使用静态的方法创建一个任务xTaskCreatePinnedToCore指定任务运行的核心(最后一个参数)vTaskDelete()删…...
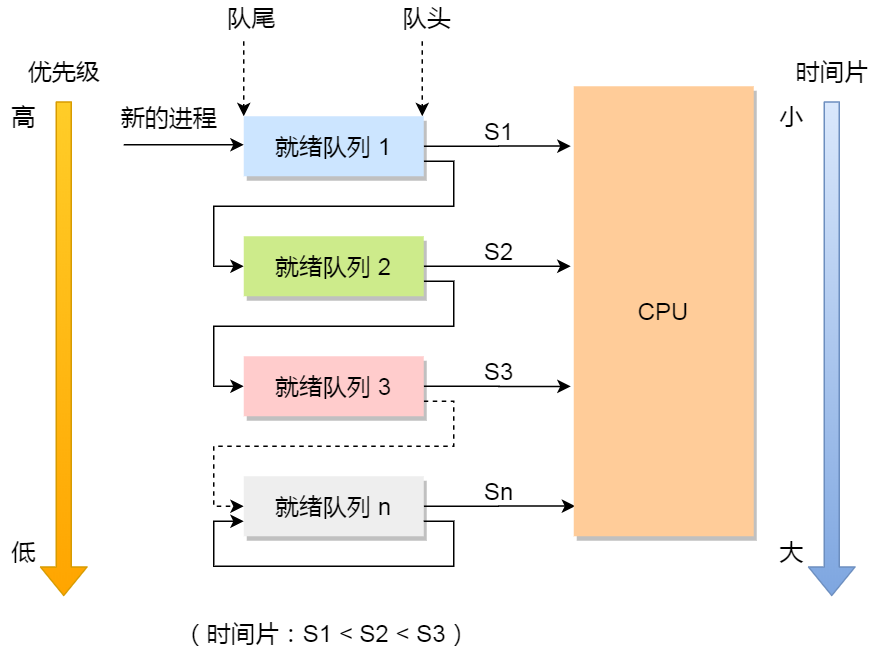
【操作系统】面试官都爱问的进程调度算法
【操作系统】面试官都爱问的进程调度算法 文章目录【操作系统】面试官都爱问的进程调度算法先来先服务调度算法最短作业优先调度算法高响应比优先调度算法时间片轮转调度算法最高优先级调度算法多级反馈队列调度算法进程调度算法也称 CPU 调度算法,毕竟进程是由 CPU…...
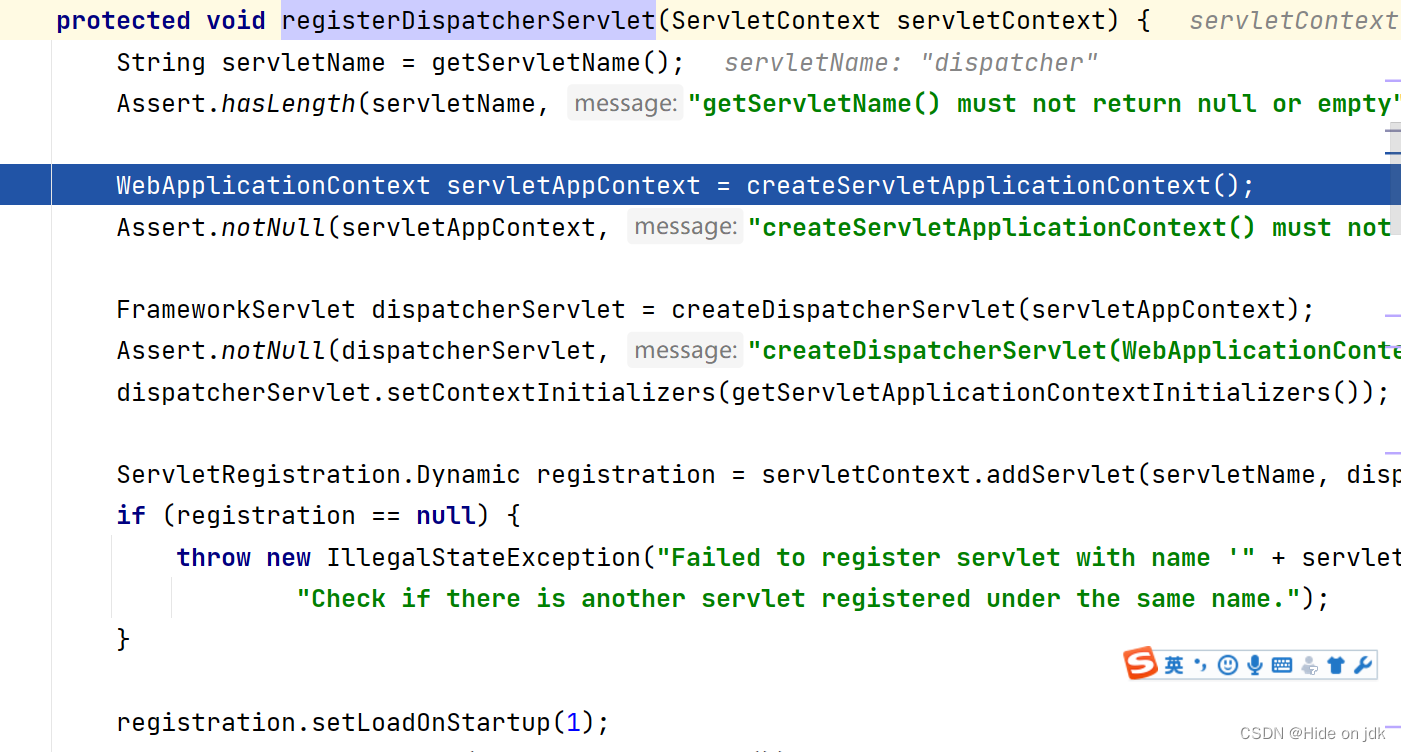
Spring-Web spi机制解析
org.springframework.web.SpringServletContainerInitializer#onStartup 在这里打个断点,查看程序是否会进来 可以发现程序进来了:主要spi机制,看看这里做了什么操作? 去寻找所有实现了WebApplicationInitializer的类 将符合条件…...

数据结构|将链表中小于0的数全部放在大于0的数的前面
题1: 某带头结点的非空单链表L中所有元素为整数,结点类型定义如下: typedef struct node { int data; struct node *next; } LinkNode; 设计一个尽可能高效的算法,将所有小于零的结点移到所有大于等于零的结点的前面。 分…...

分享106个ASP影音娱乐源码,总有一款适合您
分享106个ASP影音娱乐源码,总有一款适合您 106个ASP影音娱乐源码下载链接:https://pan.baidu.com/s/13k8UaJrCci_z4Q0gQbtDtg?pwdjq44 提取码:jq44 Python采集代码下载链接:采集代码.zip - 蓝奏云 我的博客地址:亚…...

win10 PyCharm Anaconda过程记录
1、Anaconda用来配置不同的虚拟环境 进入 Anaconda Prompt 输入conda activate Hui(此为自己创建的放置虚拟环境的文件夹) 编译运行过程中出现No module named seaborn后 pip install seaborn...
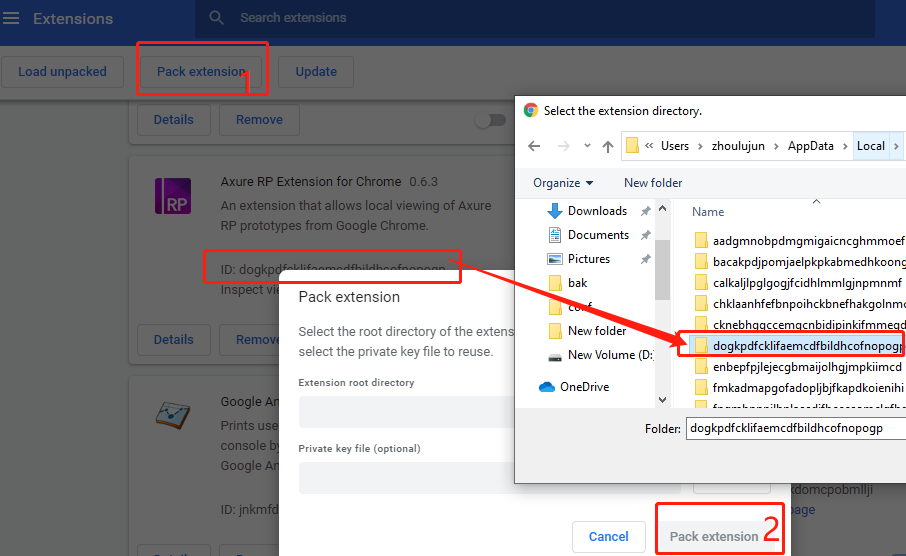
Chrome扩展程序导出备份与本地导入浏览器
现在即使在国内下载个chrome,转个插件也千难万难。现在科学上网也越来越难,由于众所周知的原因,连qiang这个话题都是敏感词。哀默于心死,还是回避这个话题 只要把之前装的chrome打包,然后再重新安装一遍。操作步骤如下…...
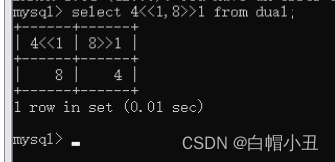
mysql常用运算符
mysql常用运算符一、去重和空值1.distinct2.null参与运算3.用ifnull函数解决问题二、比较运算符三、dual伪表和数值运算1.常规运算2.比较运算符3.<>安全相等四、常用正则相关的比较运算符1.基本运算符2.模糊查询3.正则表达式五、逻辑运算符六、位运算总结一、去重和空值 …...

PyTorch 深度学习框架:优雅而简洁的代码实现
PyTorch 是由 Facebook 发布的深度学习框架,旨在为研究人员和工程师提供快速、灵活和简单的实验平台。与其他框架相比,PyTorch 具有简洁的 API 和灵活的动态计算图,使得构建和训练深度神经网络变得更加优雅和简洁。本文将介绍 PyTorch 的基本…...

【SpringMVC】请求重定向和转发
forward:表示转发 处理器方法返回ModelAndView,实现转发forward 语法: setViewName("forward:视图文件完整路径") forward特点: 不和视图解析器一同使用,就当项目中没有视图解析器redirect:表示重定向 处理…...

Vue中@click的常见修饰符
在 Vue 的click事件中,可以使用以下修饰符: .stop:阻止事件继续传播。.prevent:阻止默认事件。.capture:使用事件捕获模式。.self:只当事件是从侦听器绑定的元素本身触发时才触发回调。.once:只…...
软件测试面试复盘:技术面没有难倒我,hr面被虐的体无完肤
一般提到面试,肯定都会想问一下面试结果,我就大概的说一下面试结果,哈哈,其实不太想说,因为挺惨的,并没有像很多大佬一样 ”已拿字节阿里腾讯各大厂offer”,但是毕竟是自己的经历,无…...

vue实现鼠标移入移出事件+解决鼠标事件没有反应
鼠标移入移出事件代码 <div mouseenter"onMouseOver(item)" mouseleave"onMouseOut"></div> methods methods:{// 鼠标移入onMouseOver(item){console.log(item, 鼠标进来了);},// 鼠标移出onMouseOut(){console.log(鼠标出去了);}, }, 这…...
右键移动文件.cmd
REM xcopy /yis %1% % % %D:\test\% REM https://zhuanlan.zhihu.com/p/38330443 不能移动文件夹 不知道为什么 xcopy(拷贝目录文件、目录结构的指令)_尚可名片 写了个JAVA程序,怎样实现在win选中文件后,右键发送到我的程序&am…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...

ubuntu22.04有线网络无法连接,图标也没了
今天突然无法有线网络无法连接任何设备,并且图标都没了 错误案例 往上一顿搜索,试了很多博客都不行,比如 Ubuntu22.04右上角网络图标消失 最后解决的办法 下载网卡驱动,重新安装 操作步骤 查看自己网卡的型号 lspci | gre…...

热烈祝贺埃文科技正式加入可信数据空间发展联盟
2025年4月29日,在福州举办的第八届数字中国建设峰会“可信数据空间分论坛”上,可信数据空间发展联盟正式宣告成立。国家数据局党组书记、局长刘烈宏出席并致辞,强调该联盟是推进全国一体化数据市场建设的关键抓手。 郑州埃文科技有限公司&am…...
