6.10 谱分解
文章目录
- 计算方法
- 代码实现
计算方法
单纯矩阵normal matrix指的是符号ATA=AATA^TA=AA^TATA=AAT的矩阵,他们的特征值互异。此外,单纯矩阵还有个特点,他们的特征空间彼此正交。
对于单纯矩阵,存在以下的谱定理Spectral theorem:
单纯矩阵可以分解为以下矩阵相加的形式:
A=∑i=1nλiviviHA=\sum_{i=1}^n\lambda_iv_iv_i^H A=i=1∑nλiviviH
公式中,viv_ivi是特征值λi\lambda_iλi对应的单位特征向量。
把矩阵分解为这种形式就是谱分解Spectral Decompostion。所以谱分解挺容易的,求出特征值和特征向量就行了。
以下是一个矩阵谱分解的例子:
(3000020000−20000−1)=3(1000000000000000)+2(0000010000000000)−2(0000000000100000)−(0000000000000001)\begin{pmatrix}3 & 0 & 0 & 0\\ 0 & 2 & 0 & 0\\ 0 & 0 & -2 & 0\\ 0 & 0 & 0 & -1\\ \end{pmatrix}\\ = 3 \begin{pmatrix}1 & 0 & 0 & 0\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0\\ \end{pmatrix}+2 \begin{pmatrix}0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0\\ \end{pmatrix} -2 \begin{pmatrix}0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0\\ \end{pmatrix} -\begin{pmatrix}0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1\\ \end{pmatrix} 3000020000−20000−1=31000000000000000+20000010000000000−20000000000100000−0000000000000001
代码实现
特征值可以用海森堡法求解,特征向量可以用齐次方程组求解的方法求得,最后注意单位化就行了。以下是python代码:
# 谱分解def spectral_decomposition(self):# 求特征值from com.youngthing.mathalgorithm.linearalgebra.hessenberg import Matrix as Meigen_values = M(self.__vectors).eigen_values()spectral_matrices = []for i, e in enumerate(eigen_values):# 单纯矩阵的几何重数为1eigen_vector = self.eigen_vector(e)[0]vector_len = Matrix.vector_len(eigen_vector)eigen_vector = matrix_utils.mul_num(eigen_vector, 1 / vector_len)x = Matrix([eigen_vector])spectral_matrices.append(x * x.transpose_matrix())return eigen_values, spectral_matrices
相关文章:

6.10 谱分解
文章目录计算方法代码实现计算方法 单纯矩阵normal matrix指的是符号ATAAATA^TAAA^TATAAAT的矩阵,他们的特征值互异。此外,单纯矩阵还有个特点,他们的特征空间彼此正交。 对于单纯矩阵,存在以下的谱定理Spectral theorem&…...

MySQL入门篇-MySQL 行转列小结
备注:测试数据库版本为MySQL 8.0 需求:求emp表各个岗位的工资之和,如无,用0代替 如需要scott用户下建表及录入数据语句,可参考:scott建表及录入数据sql脚本 CASE语法 SELECT deptno,ifnull(sum(case when job MANAGER then sal else 0 …...

项目管理常见的十大难题及其症状
01缺少维护文档时常,项目工作紧张时,第一个去掉的就是文档工作。有时即使项目有时间,也不会创建文档;或是创建了文档,却很少在项目进行过程中维护它。症状产品与需求文档不符;技术文档过时,无法保证技术的延…...

技术方案模板
0.基本原则 1.可量化,很大、很多、很高 到底是多少?基本没影响,到底有没有影响什么情况下有影响? 2.可实施,结合实际情况最终可落地 3.可指导,非方案制定人能理解,能在尽量少的人工沟通的情况下实现方案 4.可复用,设计的方案,再次出现类似需求时可以做到少开发或不…...

MySQL中对于单表和多表的操作
一、单表查询素材: 表名:worker-- 表中字段均为中文,比如 部门号 工资 职工号 参加工作 等显示所有职工的基本信息。mysql8.0 [chap03]>select * from worker;查询所有职工所属部门的部门号,不显示重复的部门号。mysql8.0 [cha…...

MFI认证
一、什么是MFI认证? 苹果MFI认证,是苹果公司(Apple Inc.)对其授权配件厂商生产的外置配件的一种使用许可,MFi认证是apple公司Made for iPhone/iPad/iPod的英文缩写。是指分别为连接iPhone/iPad/iPod而特别设计的电子配件。 [图片] 二、iOS外设连接的几种方式 [图片] 这…...

Vue中mixins的使用
文章目录mixins介绍mixins特点mixins介绍 Mixins:在引入组件之后与组件中的对象和方法进行合并,相当于扩展了父组件的对象与方法,可以理解为形成了一个新的组件。混入 (mixins):是一种分发 Vue 组件中可复用功能的非常灵活的方式…...
【PyQt】PyQt学习(一)框架介绍+环境搭建
简介 写在最前面的话 在决定学习、使用一个框架之前需要考量如下几点: 框架运行效果;框架应用范围;框架学习成本和迁移成本;实现自己所需功能的开发效率; 只有综合考量如上四个方面,才能更好地选择适合…...

浅谈前端设计模式:策略模式和状态模式的异同点
一、策略模式 策略模式是定义一系列的算法,把它们一个个封装起来, 并且使它们可相互替换。 而且策略模式是重构小能力,特别适合拆分“胖逻辑”。 这个定义乍一看会有点懵,不过通过下面的例子就能慢慢理解它的意思。 先来看一个真实场景 某次活动要做…...

线性杂双功能PEG试剂OPSS-PEG-Acid,OPSS-PEG-COOH,巯基吡啶聚乙二醇羧基
英文名称:OPSS-PEG-COOH,OPSS-PEG-Acid 中文名称:巯基吡啶-聚乙二醇-羧基 OPSS-PEG-COOH是一种具有OPSS和羧基的线性杂双功能PEG试剂。它是一种有用的带有PEG间隔基的交联剂。OPSS代表正吡啶基二硫化物或邻吡啶基二硫代,与硫醇、…...

开发微服务电商项目演示(四)
一,网关服务限流熔断降级第1步:启动sentinel-dashboard控制台和Nacos注册中心服务第2步:在网关服务中引入sentinel依赖<!-- sentinel --> <dependency><groupId>com.alibaba.cloud</groupId><artifactId>sprin…...
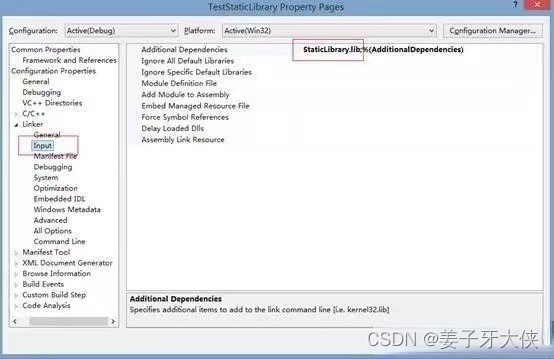
【C语言学习笔记】:静态库
一、什么是库 库是写好的现有的,成熟的,可以复用的代码。现实中每个程序都要依赖很多基础的底层库,不可能每个人的代码都从零开始,因此库的存在意义非同寻常。 本质上来说库是一种可执行代码的二进制形式,可以被操作…...

社科院与杜兰大学中外合作办学金融管理硕士——30+的年龄在职读研有必要吗?
说起读研,年龄在什么区间最合适呢?上次有位咨询的同学反馈年龄已经快35岁了,有一份不错的工作,但又不甘心止步于此,想要通过提升学历升职加薪,但又纠结自己是否能静下心来学习、是否能顺利毕业、拿到的证书…...
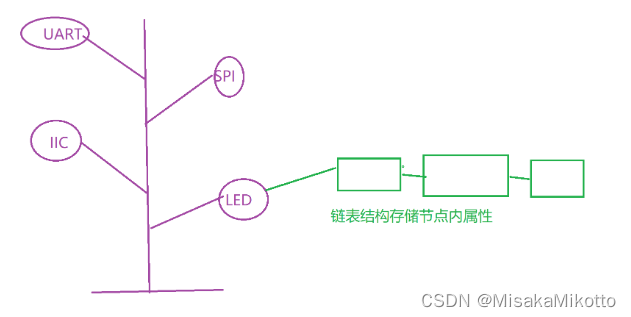
2.13作业【设备树解析,按自己理解】
设备树定义 设备树(device tree是描述硬件信息的一种树形结构,设备书文件在linux内核启动后被内核解析。描述一个硬件设备信息的节点我们叫做设备节点,一个设备节点内部包含当前硬件的多个不同属性,相同节点不同属性是以链式结构存…...

《NFL星计划》:巴尔的摩乌鸦·橄榄1号位
巴尔的摩乌鸦(英语:Baltimore Ravens)是一支职业美式橄榄球球队位于马里兰州的巴尔的摩。他们现时为美国美式橄榄球联合会的北区进行比赛,其主场为M&T银行体育场。乌鸦队曾在2000年和2012年取得超级碗冠军。 巴尔的摩乌鸦 成…...
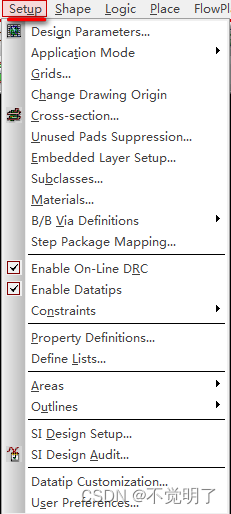
Allegro如何设置自动保存和自动保存的时间操作指导
Allegro如何设置自动保存和自动保存的时间操作指导 做PCB设计的时候,自动保存软件是一个必要的功能,Allegro同样支持设置自动保存,而且可以设置自动保存的时间。 如下图 具体操作如下 点击Setup点击User Preferences...
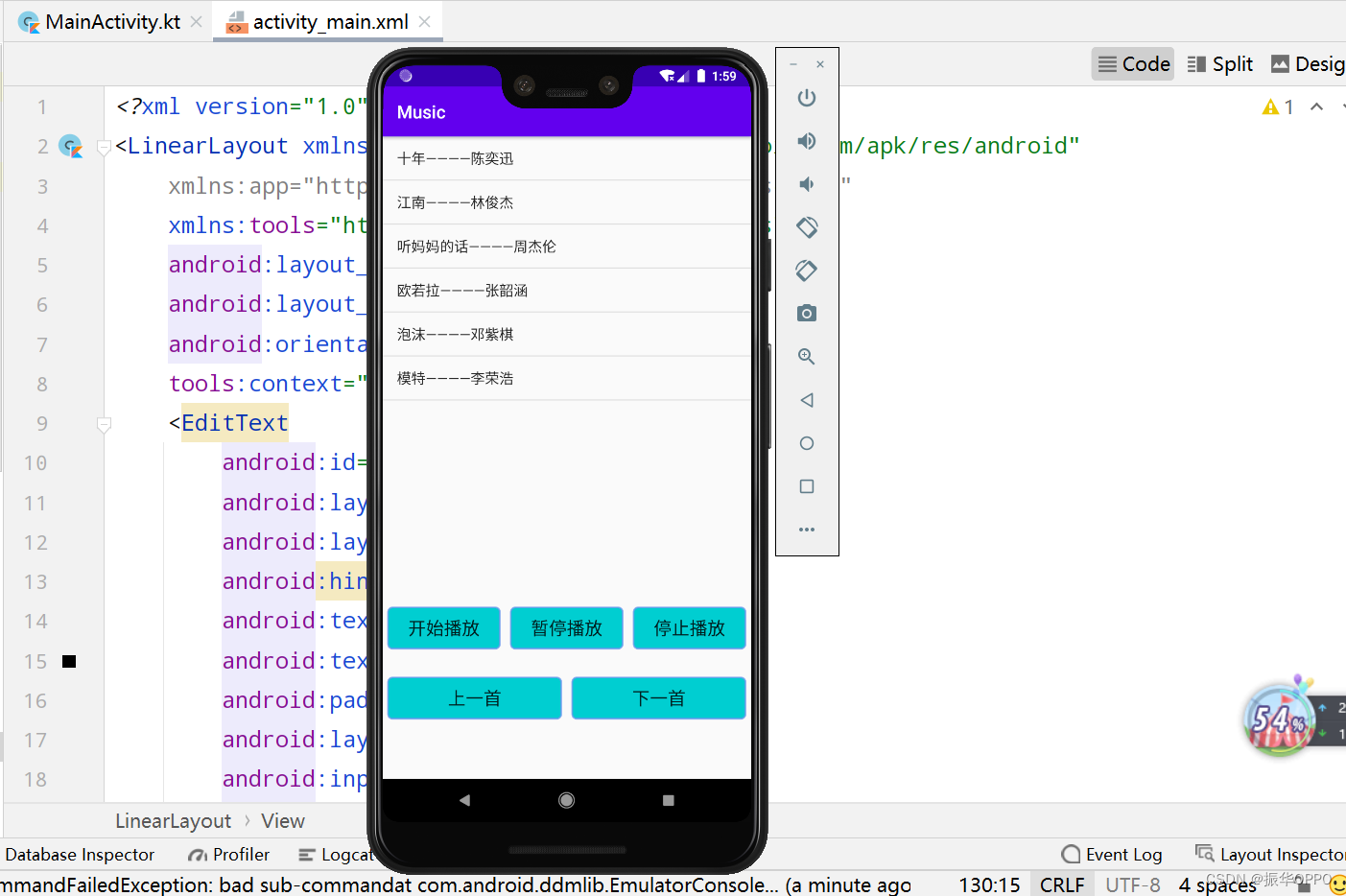
Kotlin实现简单音乐播放器
关于音乐播放器,我真的是接触比较多,听歌作为我第一大爱好,之前也用Java设计过音乐播放器,感兴趣的同学可以阅读:Android Studio如何实现音乐播放器(简单易上手)和 Android Studio实现音乐播放器…...
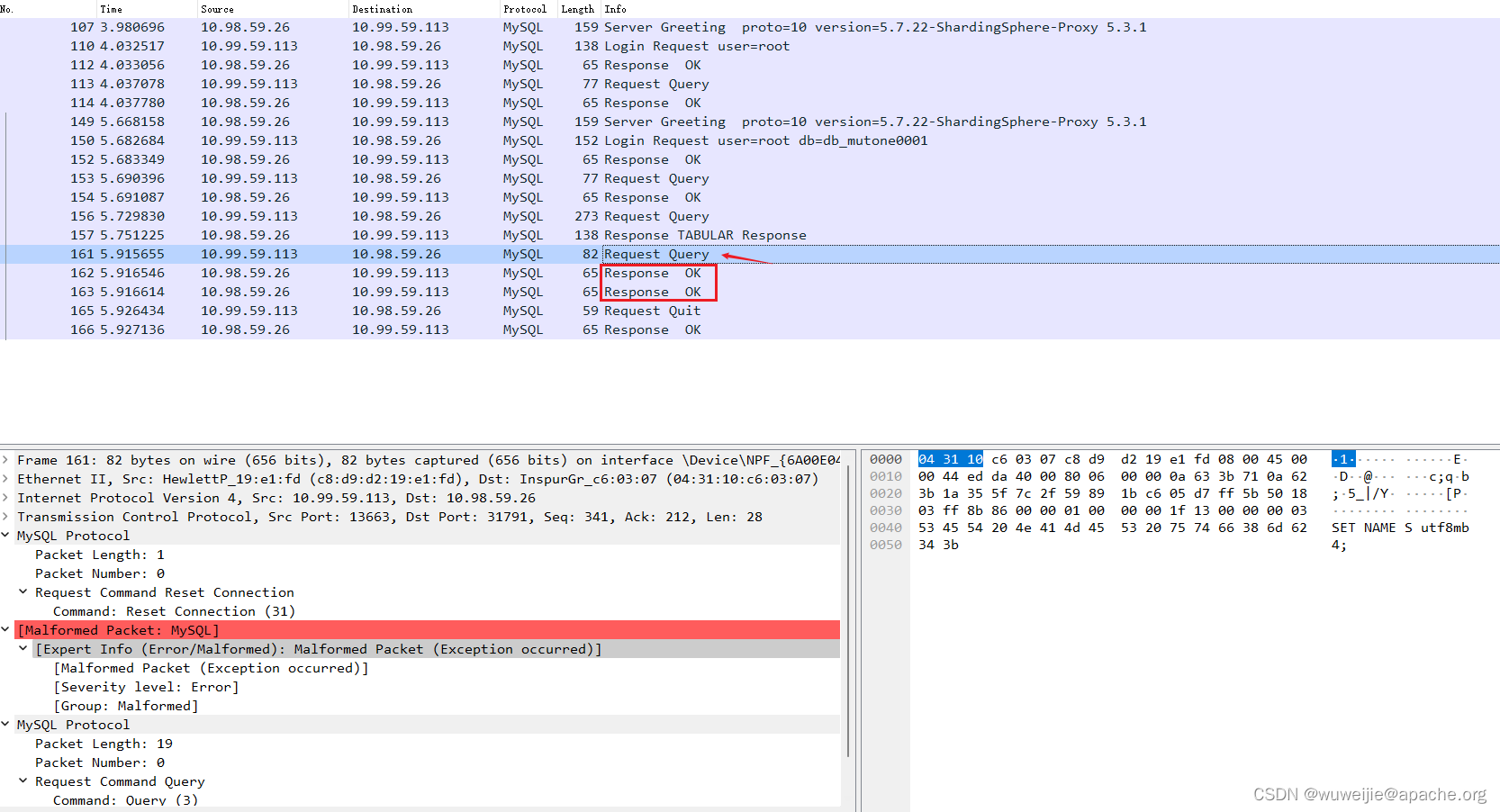
ShardingSphere-Proxy 数据库协议交互解读
数据库协议对于大部分开发者来说算是比较冷门的知识,一般的用户、开发者都是通过现成的数据库客户端、驱动使用数据库,不会直接操作数据库协议。不过,对数据库协议的特点与流程有一些基本的了解,有助于开发者在排查数据库功能、性…...
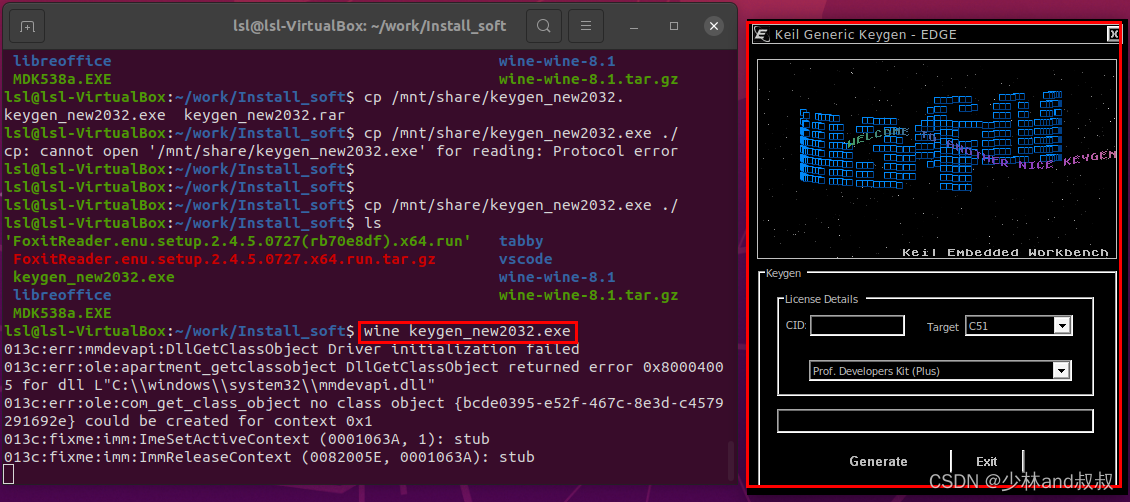
基于ubuntu20.4的wine的MDK5软件的安装
本文基于ubuntu20.4安装MDK5的keil软件,由于MDK不提供linux版本的安装软件,因此需要利用wine软件来安装MDK5软件,具体流程包括wine软件安装、MDK5安装及MDK5的lic添加等3部分内容。具体流程如下所示: (一)…...
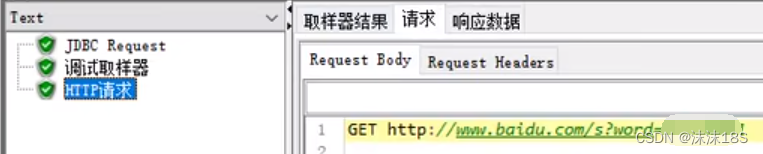
Jmeter之直连数据库框架搭建简介
案例简介 通过直连数据库让程序代替接口访问数据库,如果二者预期结果不一致,就找到了程序的缺陷。 下面通过一个案例分析讲解如何实现:获取某个字段值,放在百度上搜索。 实现方式 1、Jmeter本身不具备直连数据库的功能…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...

在 Spring Boot 中使用 JSP
jsp? 好多年没用了。重新整一下 还费了点时间,记录一下。 项目结构: pom: <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://ww…...

Ubuntu系统多网卡多相机IP设置方法
目录 1、硬件情况 2、如何设置网卡和相机IP 2.1 万兆网卡连接交换机,交换机再连相机 2.1.1 网卡设置 2.1.2 相机设置 2.3 万兆网卡直连相机 1、硬件情况 2个网卡n个相机 电脑系统信息,系统版本:Ubuntu22.04.5 LTS;内核版本…...

消防一体化安全管控平台:构建消防“一张图”和APP统一管理
在城市的某个角落,一场突如其来的火灾打破了平静。熊熊烈火迅速蔓延,滚滚浓烟弥漫开来,周围群众的生命财产安全受到严重威胁。就在这千钧一发之际,消防救援队伍迅速行动,而豪越科技消防一体化安全管控平台构建的消防“…...
