第十四届蓝桥杯大赛软件赛省赛(C/C++B组)
目录
- 试题 A. 日期统计
- 1.题目描述
- 2.解题思路
- 3.模板代码
- 试题 B.01 串的熵
- 1.题目描述
- 2.解题思路
- 3.模板代码
- 试题 C. 冶炼金属
- 1.题目描述
- 2. 解题思路
- 3.模板代码
- 试题 D. 飞机降落
- 1.题目描述
- 2. 解题思路
- 3.模板代码
- 试题 E. 接龙数列
- 1.题目描述
- 2. 解题思路
- 3.模板代码
- 试题 F. 岛屿个数
- 1.题目描述
- 2. 解题思路
- 3.模板代码
- 试题 G. 子串简写
- 1.题目描述
- 2. 解题思路
- 3.模板代码
- 试题 H.整数删除
- 1.题目描述
- 2. 解题思路
- 3.模板代码
- 试题 I. 景区旅游
- 1.题目描述
- 2. 解题思路
- 3.模板代码
- 试题 J. 砍树
- 1.题目描述
- 2. 解题思路
- 3. 模板代码
部分题暂更补代码,欢迎评论区交流
试题 A. 日期统计
1.题目描述
小蓝现在有一个长度为 100 的数组,数组中的每个元素的值都在 0 到 9 的
范围之内。数组中的元素从左至右如下所示:
5 6 8 6 9 1 6 1 2 4 9 1 9 8 2 3 6 4 7 7 5 9 5 0 3 8 7 5 8 1 5 8 6 1 8 3 0 3 7 9 2
7 0 5 8 8 5 7 0 9 9 1 9 4 4 6 8 6 3 3 8 5 1 6 3 4 6 7 0 7 8 2 7 6 8 9 5 6 5 6 1 4 0 1
0 0 9 4 8 0 9 1 2 8 5 0 2 5 3 3
现在他想要从这个数组中寻找一些满足以下条件的子序列:
-
- 子序列的长度为 888;
-
- . 这个子序列可以按照下标顺序组成一个 yyyymmddyyyymmddyyyymmdd 格式的日期,并且
要求这个日期是 202320232023 年中的某一天的日期,例如 20230902,2023122320230902,2023122320230902,20231223。
yyyyyyyyyyyy 表示年份,mmmmmm 表示月份,dddddd 表示天数,当月份或者天数的长度只
有一位时需要一个前导零补充。
- . 这个子序列可以按照下标顺序组成一个 yyyymmddyyyymmddyyyymmdd 格式的日期,并且
请你帮小蓝计算下按上述条件一共能找到多少个不同 的 2023 年的日期。
对于相同的日期你只需要统计一次即可。
2.解题思路
考虑八层循环枚举一下,中间需要进行减枝加快搜索步骤,不建议写 dfs,不然就像我一样在考场写烂,注意答案需要去重,答案为235。
3.模板代码
暂更
试题 B.01 串的熵
1.题目描述
没学过数学,暂更
2.解题思路
3.模板代码
试题 C. 冶炼金属
1.题目描述
小蓝有一个神奇的炉子用于将普通金属 OOO 冶炼成为一种特殊金属 XXX。这个
炉子有一个称作转换率的属性 VVV,VVV 是一个正整数,这意味着消耗 VVV 个普通金
属 OOO 恰好可以冶炼出一个特殊金属 XXX,当普通金属 OOO 的数目不足 VVV 时,无法
继续冶炼。
现在给出了 NNN 条冶炼记录,每条记录中包含两个整数 AAA 和 BBB,这表示本次投入了 AAA 个普通金属 OOO,最终冶炼出了 BBB 个特殊金属 XXX。每条记录都是独立
的,这意味着上一次没消耗完的普通金属 OOO 不会累加到下一次的冶炼当中。
根据这 NNN 条冶炼记录,请你推测出转换率 VVV 的最小值和最大值分别可能是多少,题目保证评测数据不存在无解的情况。
2. 解题思路
如果看过样例的话,显然答案两个上下界都是可以直接二分出来的。因为式子的结构都是 AC=B\frac{A}{C} = BCA=B。AAA 是不变的,我们先考虑二分求最小的 CCC,因为需要保证所有式子的 BBB 都不变,如果 CCC 太小,显然会有某一组的 BBB 增大,所以需要保证每一组都符合a[i]/x <= b[i]。反过来考虑求最大的 CCC, 如果 CCC 太大,显然会有某一组的 BBB 变小,需要保证每一组都符合 a[i]/x >= B。
3.模板代码
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef unsigned long long uLL;
typedef pair<int, int> PII;
#define pb(s) push_back(s);
#define SZ(s) ((int)s.size());
#define ms(s,x) memset(s, x, sizeof(s))
#define all(s) s.begin(),s.end()
const int inf = 0x3f3f3f3f;
const int mod = 1000000007;
const int N = 200010;int n;
int a[N], b[N];
bool check(LL x) {for (int i = 1; i <= n; ++i) {if (a[i] / x > b[i]) return false;}return true;
}
bool check2(LL x) {for (int i = 1; i <= n; ++i) {if (a[i] / x < b[i]) return false;}return true;
}
void solve()
{cin >> n;for (int i = 1; i <= n; ++i) cin >> a[i] >> b[i];LL l = 1, r = 1e9;while (l < r) {LL mid = l + r >> 1;if (check(mid)) r = mid;else l = mid + 1;}int s = r;l = 1, r = 1e9;while (l < r) {LL mid = l + r + 1 >> 1;if (check2(mid)) l = mid;else r = mid - 1;}cout << s << " " << r << '\n';
}
int main()
{ios_base :: sync_with_stdio(false);cin.tie(0); cout.tie(0);int t = 1;while (t--){solve();}return 0;
}
试题 D. 飞机降落
1.题目描述
NNN 架飞机准备降落到某个只有一条跑道的机场。其中第 iii 架飞机在 TiTiTi 时刻到达机场上空,到达时它的剩余油料还可以继续盘旋 DiDiDi 个单位时间,即它最早
可以于 TiTiTi 时刻开始降落,最晚可以于 Ti+DiTi + DiTi+Di 时刻开始降落。降落过程需要 LiLiLi
个单位时间。
一架飞机降落完毕时,另一架飞机可以立即在同一时刻开始降落,但是不
能在前一架飞机完成降落前开始降落。
请你判断 NNN 架飞机是否可以全部安全降落。
2. 解题思路
看 NNN 最大为10,写了个全排列,T组数据复杂度还是炸了,暂更吧 。
3.模板代码
试题 E. 接龙数列
1.题目描述
对于一个长度为 KKK 的整数数列:A1,A2,...,AKA_1, A_2, . . . , A_KA1,A2,...,AK,我们称之为接龙数列当且仅当 AiA_iAi 的首位数字恰好等于 Ai−1A_{i-1}Ai−1 的末位数字 (2≤i≤K)(2 ≤ i ≤ K)(2≤i≤K)。
例如 12,23,35,56,61,1112, 23, 35, 56, 61, 1112,23,35,56,61,11 是接龙数列;12,23,34,5612, 23, 34, 5612,23,34,56 不是接龙数列,因为 565656 的首位数字不等于 343434 的末位数字。所有长度为 111 的整数数列都是接龙数列。
现在给定一个长度为 NNN 的数列 A1,A2,...,ANA_1, A_2, . . . , A_NA1,A2,...,AN,请你计算最少从中删除多少个数,可以使剩下的序列是接龙序列?
2. 解题思路
考场读完题的时候感觉有点奇怪,发现思路还是比较简单的。首先一个数我们只需要关注其首位数字和末位数字,定以 f[i]f[i]f[i] 为以数字 iii 结尾的最长接龙序列的长度,iii 的范围是 [0,9][0,9][0,9]。对于每个数字设其首位数字为 aaa ,末尾数字为 bbb,则有转移方程:
f[b]=max(f[b],f[a]+1)f[b]=max(f[b],f[a]+1)f[b]=max(f[b],f[a]+1)
最后在 f[0]、f[1]...f[9]f[0]、f[1]...f[9]f[0]、f[1]...f[9] 取一个最大值 ansansans,答案则为 n−ansn-ansn−ans。
3.模板代码
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef unsigned long long uLL;
typedef pair<int, int> PII;
#define pb(s) push_back(s);
#define SZ(s) ((int)s.size());
#define ms(s,x) memset(s, x, sizeof(s))
#define all(s) s.begin(),s.end()
const int inf = 0x3f3f3f3f;
const int mod = 1000000007;
const int N = 200010;int n;
int a[N], b[N];
int f[10];
void solve()
{cin >> n;for (int i = 1; i <= n; ++i) {int x;cin >> x;b[i] = x % 10;string s = to_string(x);a[i] = s[0] - '0';}for (int i = 1; i <= n; ++i) {f[b[i]] = max(f[b[i]], f[a[i]] + 1);}int ans = 0;for (int i = 0; i <= 9; ++i) ans = max(ans, f[i]);cout << n - ans << '\n';
}
int main()
{ios_base :: sync_with_stdio(false);cin.tie(0); cout.tie(0);int t = 1;while (t--){solve();}return 0;
}
试题 F. 岛屿个数
1.题目描述
暂更,感觉不好写
2. 解题思路
3.模板代码
试题 G. 子串简写
1.题目描述
程序猿圈子里正在流行一种很新的简写方法:对于一个字符串,只保留首尾字符,将首尾字符之间的所有字符用这部分的长度代替。例如 internation−alizationinternation-alizationinternation−alization 简写成 i18ni18ni18n,KubernetesKubernetesKubernetes (注意连字符不是字符串的一部分)简写成 K8s,LanqiaoK8s, LanqiaoK8s,Lanqiao 简写成 L5oL5oL5o等。
在本题中,我们规定长度大于等于 KKK 的字符串都可以采用这种简写方法(长度小于 KKK 的字符串不配使用这种简写)。
给定一个字符串 SSS 和两个字符 c1c1c1 和 c2c2c2,请你计算 SSS 有多少个以 c1c1c1 开头 c2c2c2 结尾的子串可以采用这种简写?
2. 解题思路
这道题放在 G 题感觉更奇怪了,一道前缀和模板题。假设下标为 iii 的字符为 c1c1c1,那我们只需要统计在区间 [i+k−1,n][i+k-1,n][i+k−1,n]有多少个 c2c2c2 即可,前缀和预处理一下 c2c2c2 字符,直接累加答案即可,注意答案会爆int,复杂度 O(n)O(n)O(n)
3.模板代码
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef unsigned long long uLL;
typedef pair<int, int> PII;
#define pb(s) push_back(s);
#define SZ(s) ((int)s.size());
#define ms(s,x) memset(s, x, sizeof(s))
#define all(s) s.begin(),s.end()
const int inf = 0x3f3f3f3f;
const int mod = 1000000007;
const int N = 500010;int k;
string s;
char c1, c2;
int a[N];
void solve()
{cin >> k >> s >> c1 >> c2;int n = s.size();s = '?' + s;for (int i = 1; i <= n; ++i) {a[i] = (s[i] == c2);a[i] += a[i - 1];}LL ans = 0;for (int i = 1; i + k - 2 < n; ++i) {if (s[i] == c1) ans += a[n] - a[i + k - 2];}cout << ans << '\n';
}
int main()
{ios_base :: sync_with_stdio(false);cin.tie(0); cout.tie(0);int t = 1;while (t--){solve();}return 0;
}
试题 H.整数删除
1.题目描述
给定一个长度为 NNN 的整数数列:A1,A2,...,ANA_1, A_2, . . . , A_NA1,A2,...,AN。你要重复以下操作 KKK 次:
每次选择数列中最小的整数(如果最小值不止一个,选择最靠前的),将其删除。并把与它相邻的整数加上被删除的数值。
输出 KKK 次操作后的序列。
2. 解题思路
感觉是比较典的题目,但是这题好像卡常,我的代码在非官方数据TLE了大半。用优先队列维护,存入值和下标,再用一个数组cnt累计每个下标增加的和,当弹出最小的值下标为 i 时,如果此时cnt[i]不等于0,说明它实际的值需要加上cnt[i],我们将其增加后再放回优先对列,注意需要清空cnt[i]。如果此时cnt[i]等于0,那我们就成功弹出当前最小元素,这时需要将其前一个元素和后一个元素值增加,我们需要模拟链表去记录每个元素的前后元素是谁,pre[i]表示下标为i的上一个元素是谁,ne[i]表示下标为 i 的下一个元素是谁,直到堆的元素个数只剩n-k时结束循环。
评论区来个小伙伴帮忙优化下或者来个其他做法
3.模板代码
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef unsigned long long uLL;
typedef pair<int, int> PII;
#define pb(s) push_back(s);
#define SZ(s) ((int)s.size());
#define ms(s,x) memset(s, x, sizeof(s))
#define all(s) s.begin(),s.end()
const int inf = 0x3f3f3f3f;
const int mod = 1000000007;
const int N = 500010;int n, k;
int pre[N], ne[N];
LL cnt[N];
void solve()
{cin >> n >> k;priority_queue<pair<LL, int>, vector<pair<LL, int>>, greater<pair<LL, int>> >q;for (int i = 1; i <= n; ++i) {LL v;cin >> v;q.push({v, i});pre[i] = i - 1;ne[i] = i + 1;}int g = n - k;while (q.size() > g) {auto p = q.top(); q.pop();LL v = p.first, ix = p.second;if (cnt[ix]) {q.push({v + cnt[ix], ix});cnt[ix] = 0;} else {int l = pre[ix], r = ne[ix];cnt[l] += v;cnt[r] += v;ne[l] = r;pre[r] = l;}}std::vector<LL> a(n + 1);for (int i = 0; i < g; ++i) {auto p = q.top(); q.pop();a[p.second] = p.first + cnt[p.second];}for (int i = 1; i <= n; ++i) {if (a[i]) cout << a[i] << " ";}
}
int main()
{ios_base :: sync_with_stdio(false);cin.tie(0); cout.tie(0);int t = 1;while (t--){solve();}return 0;
}
试题 I. 景区旅游
1.题目描述
某景区一共有 NNN 个景点,编号 111 到 NNN。景点之间共有 N−1N − 1N−1 条双向的摆渡车线路相连,形成一棵树状结构。在景点之间往返只能通过这些摆渡车进行,需要花费一定的时间。
小明是这个景区的资深导游,他每天都要按固定顺序带客人游览其中 KKK 个景点:A1,A2,...,AKA_1, A_2, . . . , A_KA1,A2,...,AK。今天由于时间原因,小明决定跳过其中一个景点,只带游客按顺序游览其中 K−1K − 1K−1 个景点。具体来说,如果小明选择跳过 AiA_iAi,那么他会按顺序带游客游览 A1,A2,...,Ai−1,Ai+1,...,AK,(1≤i≤K)A_1, A_2, . . . , A_{i−1}, A_{i+1}, . . . , A_K, (1 ≤ i ≤ K)A1,A2,...,Ai−1,Ai+1,...,AK,(1≤i≤K)。
请你对任意一个 AiAiAi,计算如果跳过这个景点,小明需要花费多少时间在景点之间的摆渡车上?
2. 解题思路
LCALCALCA 模板题(问题是比赛写不出板子呢),首先肯定需要考虑求树上任意两点的距离。设点 u,vu,vu,v 的最近公共祖先为 zzz,定义f[i]f[i]f[i] 为点 iii 到根节点的距离,那么则有公式:
dist(u,v)=f[u]+f[v]−2∗f[z]dist(u,v)=f[u]+f[v]-2*f[z]dist(u,v)=f[u]+f[v]−2∗f[z]
先求出不跳过任何的点时需要走的距离为ans以及任意相邻两个跳点的距离。假设我们跳过四个点分别为 a,b,c,da,b,c,da,b,c,d。当跳过的点为 aaa 时,我们只需要用ans减去aaa到bbb的距离,当跳过的点为 ddd 时,我们只需要用ans减去 ccc 到 ddd 的距离,这是首尾两个点的情况。
那么当跳过的点为中间点呢?比如我们跳过的是 bbb,那么则需要用ans减去aaa到bbb以及bbb到ccc的距离,并且还需要加上aaa到ccc的距离,其余的中间点处理同理。
3.模板代码
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef unsigned long long uLL;
typedef pair<int, int> PII;
#define pb(s) push_back(s);
#define SZ(s) ((int)s.size());
#define ms(s,x) memset(s, x, sizeof(s))
#define all(s) s.begin(),s.end()
const int inf = 0x3f3f3f3f;
const int mod = 1000000007;
const int N = 200010;int n, m;
std::vector<PII> e[N];
int depth[N], fa[N][32];
LL f[N];
int root;
void bfs(int root)
{memset(depth, 0x3f, sizeof depth);depth[0] = 0, depth[root] = 1;queue<int> q;q.push(root);while (!q.empty()) {auto t = q.front();q.pop();for (auto [j, c] : e[t]) {if (depth[j] > depth[t] + 1) {depth[j] = depth[t] + 1;q.push(j);fa[j][0] = t;for (int k = 1; k <= 15; k++) {fa[j][k] = fa[fa[j][k - 1]][k - 1];}}}}
}
void dfs(int u, int fa) {for (auto [v, c] : e[u]) {if (v == fa) continue;f[v] = f[u] + c;dfs(v, u);}
}
int lca(int a, int b) {if (depth[a] < depth[b]) swap(a, b);for (int k = 15; k >= 0; k--) {if (depth[fa[a][k]] >= depth[b]) {a = fa[a][k];}}if (a == b) return a;for (int k = 15; k >= 0; --k) {if (fa[a][k] != fa[b][k]) {a = fa[a][k];b = fa[b][k];}}return fa[a][0];
}
void solve()
{cin >> n >> m;for (int i = 0; i < n - 1; ++i) {int u, v , c;cin >> u >> v >> c;e[u].push_back({v, c});e[v].push_back({u, c});}bfs(1);dfs(1, -1);std::vector<LL> g(m + 1), w(m + 1);for (int i = 1; i <= m; ++i) cin >> g[i];LL ans = 0;for (int i = 1; i < m; ++i) {int u = g[i], v = g[i + 1];int z = lca(u, v);w[i] = f[u] + f[v] - 2 * f[z];ans += w[i];}for (int i = 1; i <= m; ++i) {if (i == 1) cout << ans - w[1] << " ";else if (i == m) cout << ans - w[m - 1] << " ";else {LL res = ans - w[i] - w[i - 1];int u = g[i - 1], v = g[i + 1];int z = lca(u, v);res += f[u] + f[v] - 2 * f[z];cout << res << " ";}}
}
int main()
{ios_base :: sync_with_stdio(false);cin.tie(0); cout.tie(0);int t = 1;while (t--){solve();}return 0;
}
试题 J. 砍树
1.题目描述
给定一棵由 nnn 个结点组成的树以及 mmm 个不重复的无序数对 (a1,b1),(a2,b2),...,(am,bm)(a1, b1), (a_2, b_2),. . . , (a_m, b_m)(a1,b1),(a2,b2),...,(am,bm),其中 aiaiai 互不相同,bib_ibi 互不相同,ai,bj(1≤i,j≤m)a_i , b_j(1 ≤ i, j ≤ m)ai,bj(1≤i,j≤m)。
小明想知道是否能够选择一条树上的边砍断,使得对于每个 (ai,bi)(ai , bi)(ai,bi) 满足 aiaiai和 bibibi 不连通,如果可以则输出应该断掉的边的编号(编号按输入顺序从 111 开始),否则输出 −1-1−1。
2. 解题思路
又是 LCALCALCA 模板题啊,但我之前没做过(反正也写不出 LCALCALCA)。考虑一对无序数对的点 xxx 和 yyy ,如果我们砍掉某条边可以让这两个点不连通,那么这条边一定是从 xxx 到 yyy 路径上的一点,我们可以让从 xxx 到 yyy 路径的边权值都加1。这个操作我们可以使用树上差分。 对于 mmm 个无序数对我们都如此操作,最后如果某条边的权值为 mmm 则说明它符合条件,我们选出符合条件编号最大的那条边就是答案,如果没有权值为 mmm 的边则说明无解。
3. 模板代码
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef unsigned long long uLL;
typedef pair<int, int> PII;
#define pb(s) push_back(s);
#define SZ(s) ((int)s.size());
#define ms(s,x) memset(s, x, sizeof(s))
#define all(s) s.begin(),s.end()
const int inf = 0x3f3f3f3f;
const int mod = 1000000007;
const int N = 200010;int n, m;
std::vector<int> e[N];
int depth[N], fa[N][32];
int f[N];
int root;
int ans;
map<PII, int> mp;
void bfs(int root)
{ms(depth, 0x3f);depth[0] = 0, depth[root] = 1;queue<int> q;q.push(root);while (!q.empty()) {auto t = q.front();q.pop();for (int j : e[t]) {if (depth[j] > depth[t] + 1) {depth[j] = depth[t] + 1;q.push(j);fa[j][0] = t;for (int k = 1; k <= 15; k++) {fa[j][k] = fa[fa[j][k - 1]][k - 1];}}}}
}
int lca(int a, int b) {if (depth[a] < depth[b]) swap(a, b);for (int k = 15; k >= 0; k--) {if (depth[fa[a][k]] >= depth[b]) {a = fa[a][k];}}if (a == b) return a;for (int k = 15; k >= 0; --k) {if (fa[a][k] != fa[b][k]) {a = fa[a][k];b = fa[b][k];}}return fa[a][0];
}
int dfs(int u, int fa) {int res = f[u];for (auto v : e[u]) {if (v == fa) continue;int g = dfs(v, u);if (g == m) {ans = max(ans, mp[ {v, u}]);}res += g;}return res;
}
void solve()
{cin >> n >> m;for (int i = 0; i < n - 1; ++i) {int u, v;cin >> u >> v;mp[ {u, v}] = mp[ {v, u}] = i + 1;e[u].push_back(v);e[v].push_back(u);}bfs(1);for (int i = 0; i < m; ++i) {int u, v;cin >> u >> v;int z = lca(u, v);f[u]++;f[v]++;f[z] -= 2;}dfs(1, -1);cout << (ans == 0 ? -1 : ans) << '\n';
}
int main()
{ios_base :: sync_with_stdio(false);cin.tie(0); cout.tie(0);int t = 1;while (t--){solve();}return 0;
}
相关文章:
)
第十四届蓝桥杯大赛软件赛省赛(C/C++B组)
目录试题 A. 日期统计1.题目描述2.解题思路3.模板代码试题 B.01 串的熵1.题目描述2.解题思路3.模板代码试题 C. 冶炼金属1.题目描述2. 解题思路3.模板代码试题 D. 飞机降落1.题目描述2. 解题思路3.模板代码试题 E. 接龙数列1.题目描述2. 解题思路3.模板代码试题 F. 岛屿个数1.题…...

Python生成随机验证码
pip install pillow 实现代码 import random from PIL import Image, ImageDraw, ImageFont,ImageFilterdef check_code(width120, height30, char_length5, font_filekumo.ttf, font_size28):code []img Image.new(modeRGB, size(width, height), color(255, 255, 255))draw…...
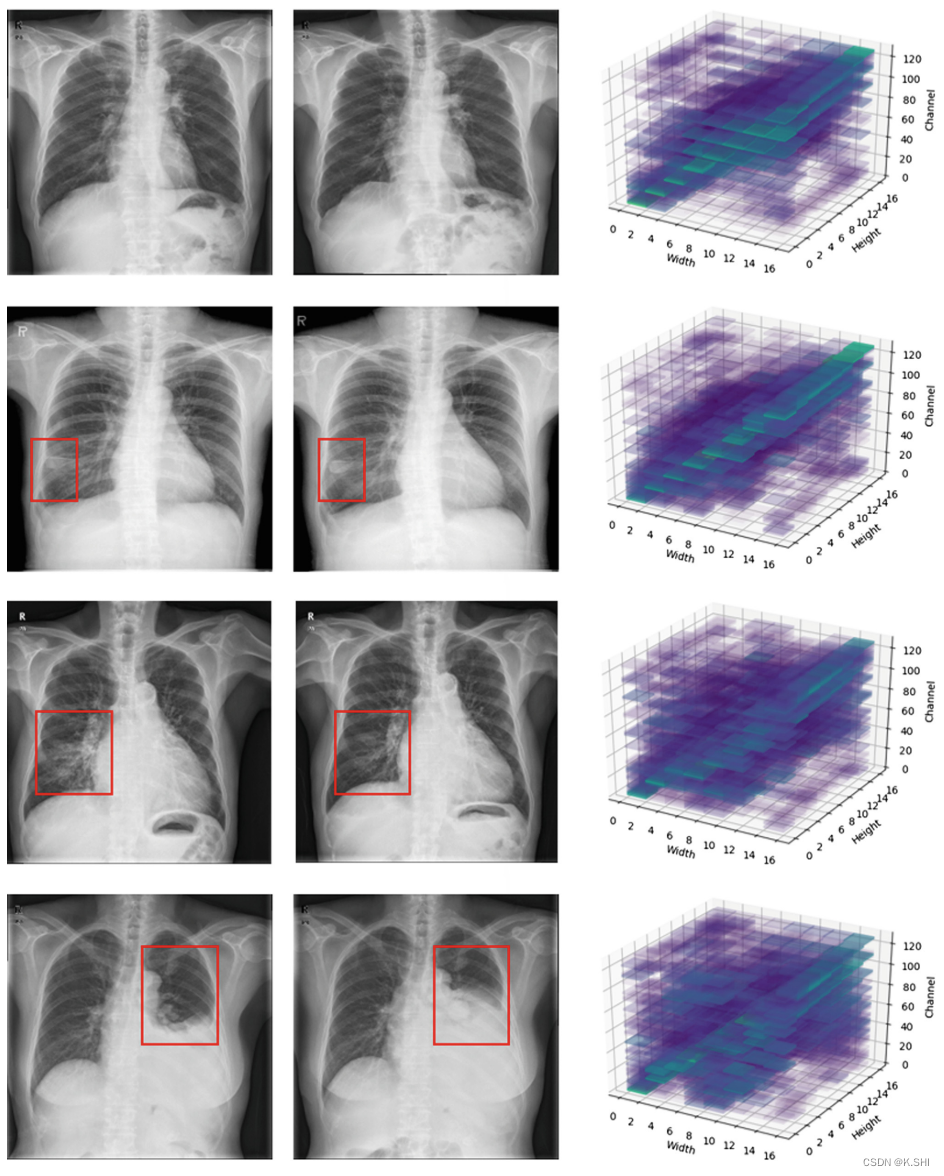
Longitudinal Change Detection on Chest X-rays Using Geometric Correlation Maps
文章来源:[MICCAI2019] Keywords:Chest X-ray;Longitudinal analysis;Change detection;Geometric correlation 一、本文提出的问题以及解决方案 在胸部X-ray图像的诊断中,医生会考虑与先前检查相比病变的…...

5年功能测试的一些心得
一、前言 功能测试是测试工程师的基础功,很多人功能测试还做不好,就想去做性能测试、自动化测试。很多人对功能测试的理解就是点点点,如何自己不用心去悟,去研究,那么你的职业生涯也就停留在点点点上了。在这里&#…...
在外包做了3年测试,离职后却成功入职字节跳动.....
最近换了份工作,当时和群里的朋友也聊过换工作的话题,他们都觉得这是一次非常冒险的行为,说我这是一次豪赌——成了会有更好的职业发展,没成可能就会出现两三年的发展断层,甚至影响职业生涯路径。一步错,步…...
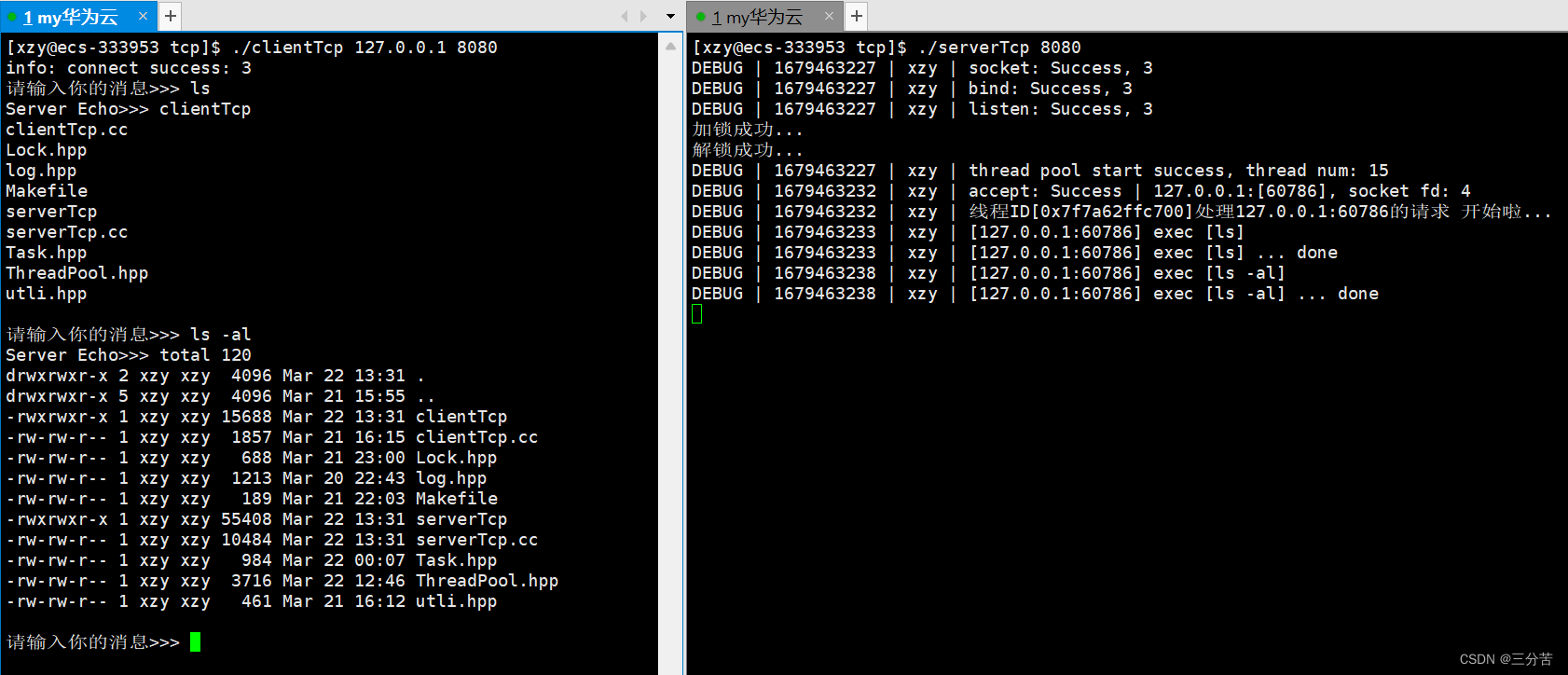
网络编程套接字( TCP )
目录 1、实现一个TCP网络程序(单进程版) 1.1、服务端serverTcp.cc文件 服务端创建套接字 服务端绑定 服务端监听 服务端获取连接 服务端提供服务 服务端main函数命令行参数 服务端serverTcp.cc总代码 1.2、客户端clientTcp.cc文件 客户端main函数命令行…...

QT 判断当前操作系统是否为 Windows 8 及以下版本
判断当前操作系统是否为 Windows 8 及以下版本,可以使用 QSysInfo 类中的静态函数 QSysInfo::windowsVersion(),其返回值是一个 QOperatingSystemVersion 类型的对象,包含了当前操作系统的主版本号、次版本号和补丁版本号。我们可以通过比较主…...

走进小程序【五】微信小程序架构之【逻辑层】详解
文章目录🌟前言🌟小程序架构🌟逻辑层 App Service🌟注册小程序🌟注册页面🌟使用 Page 构造器注册页面🌟在页面中使用 behaviors🌟使用 Component 构造器构造页面🌟页面生…...

mysql workbench使用教程
mysql workbench使用教程1、打开workbench,显示如下界面,点击2、连接建立好之后,点击已经建立好的连接,连接mysql服务器1、打开workbench,显示如下界面,点击 填写信息 密码是之前安装MySQL时设置的密码 点击…...

蓝易云:Linux系统常用命令-系列【3】
在Linux中,有许多常用的命令可以用来管理文件、目录、进程等。下面是一些常用的Linux命令的介绍。 1. cd:改变当前目录。例如,cd /home。 2. ls:列出指定目录下的所有文件和子目录。例如,ls -al。 3. rm:…...
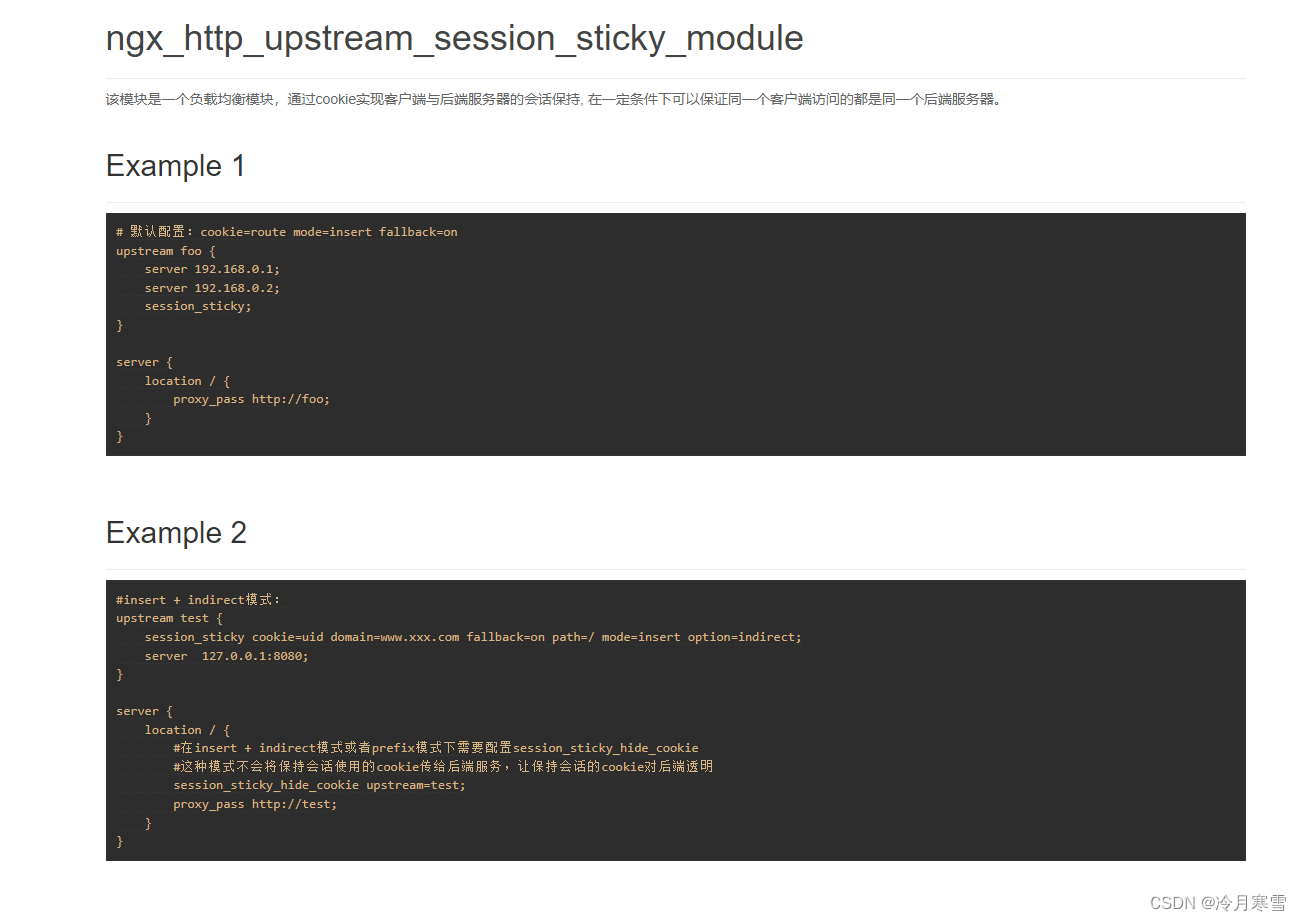
Nginx实现会话保持,集群模式下session域共享
前言 生产环境下,多数系统为了应对线上多种复杂情况而进行了集群架构的部署,保证系统的高性能、价格有效性、可伸缩性、高可用性等。通常将生产环境下的域名指向Nginx服务,通过它做HTTP协议的Web负载均衡。 session是什么 在计算机中&…...

【SpringMVC】6—SpringMVC拦截器
⭐⭐⭐⭐⭐⭐ Github主页👉https://github.com/A-BigTree 笔记链接👉https://github.com/A-BigTree/Code_Learning ⭐⭐⭐⭐⭐⭐ 如果可以,麻烦各位看官顺手点个star~😊 如果文章对你有所帮助,可以点赞👍…...

【算法】插入排序
插入排序实现思路:将一个新的数,和前面的比较,只要当前数小于前一个则和前一个交换位置,否则终止;「时间复杂度:O(N^2);」「空间复杂度:O(1)」 一、标准方式 function insertSort(a…...
java servlet 期刊在线投稿系统jsp编程sqlserver数据库mvc模式开发计算机网页设计
一、源码特点 java servlet 期刊在线投稿系统是一套完善的java web信息管理系统,对理解JSP java编程开发语言有帮助,系统采用serlvetdaobean,系统具有完整的源代码和数据库,系统 主要采用B/S模式开发。 java servlet 期刊在线…...

命名空间和程序集
目录 一、什么是命名空间 1. 命名空间的作用 2. 命名空间跨文件伸展 3.嵌套命名空间 二、using指令 1. using命名空间指令 2. using别名指令 三、程序集的结构 1. 程序集标识符 2.强命名程序集 一、什么是命名空间 1. 命名空间的作用 命名空间是共享命名空间名的一组…...
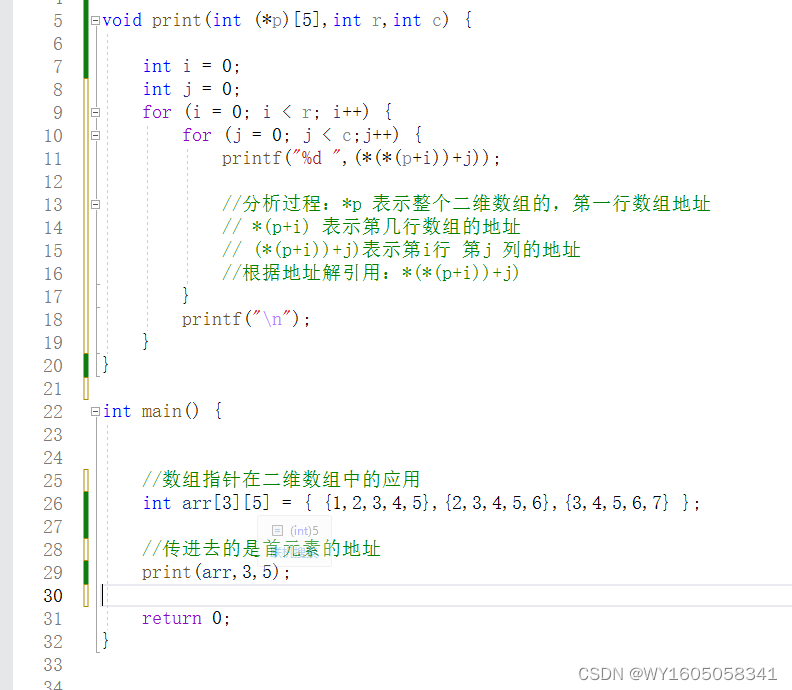
108、指针进阶
数组名是数组首元素的地址 但是有两个例外: 1、sizeof(数组名) --数组名表示整个数组,计算的是整个数组的大小,单位是 字节 byte。 2、&数组名 --数组名表示整个数组,取出的是整个数组的地址。 二…...

arm平台交叉编译rt-tests
如果要为ARM平台添加libnuma-dev库,需要在x86平台上进行交叉编译,生成ARM平台可用的库文件。具体步骤如下: 1. ARM平台的交叉编译工具链,例如arm-linux-gnueabihf,可以使用以下命令安装: sudo apt-get in…...
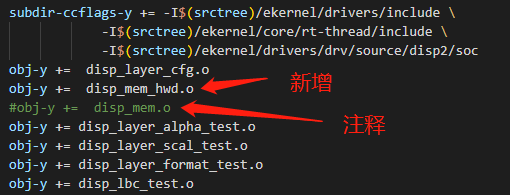
Melis4.0[D1s]:5.测试笔记 - 修改显示测试源码
文章目录1.将显示命令参数固化2.disp_mem源码阅读3.Melis子目录Makefile编写本文是下一篇文章Melis4.0[D1s]:6.mango-MQ-R基于Melis移植lvgl 的基础知识。 1.将显示命令参数固化 从上一篇文章《Melis4.0[D1s]:4.测试笔记 - 内嵌的显示命令》知道,只要2个命令就可以…...

yolov7目标检测:基于自定义数据集完成检测、训练、测试
文章目录 前言一、环境与文件准备1.1、环境配置1.2、源码下载1.3、权重文件下载1.4、详解源码中的文件夹与文件1.5、详解配置参数二、检测模型(detect.py)2.1、自定义检测数据准备2.2、配置参数2.2.1、方式一:打开Pycharm,进入Terminal,输入指令开始检测2.2.2、方式二:点…...

托福高频真词List13 // 附托福TPO阅读真题
目录 4.4单词 生词 熟词 4.5真题 4.4单词 生词 🫐damagemutilatev.损害🫐outlyingfarfar from the centeradj.偏远的🫐posterity[pɑːˈsterəti]further generationn.后代🫐🫐premiseassumpti…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...
