【面试题】JavaScript中递归的理解

大厂面试题分享 面试题库
后端面试题库 (面试必备) 推荐:★★★★★
地址:前端面试题库
递归 Recursion
To iterate is human, to recurse, divine. 理解迭代,神理解递归。
本文会以 JavaScript为主、有部分 Rust 举例说明。
概述
递归就是程序 函数自己 调用自己。递归需要有边界条件、递归前进段和递归返回段。当边界条件不满足时,递归前进;当边界条件满足时,递归返回。
帕斯卡三角: 从递推开始理解

在中国 帕斯卡三角 叫杨辉三角,因为在中国 杨辉三角 的记录比欧洲 帕斯卡三角记录早了几百年。
能产生递归的条件
调用自身:以最小的函数处理问题,产生的新问题与原问题有着相同的形式。
递归出口:递归考虑有限的问题,出口就是递归调用最后一次调用的出口
递归与循环的区别
循环是满足一定条件,重复执行同一段代码片段。而递归是函数,不断调用自己的行为。常见有 for-in/for-of 循环,而递归常见的有数学问题:fibonacci 函数。
缺点
耗内存,可以使用尾回调
回溯(Backtrack)
一个递归调用的过程,就是回溯。
回溯是一种算法思想,它是用递归实现的。
用一个比较通俗的说法来解释递归和回溯: 我们在路上走着,前面是一个多岔路口,因为我们并不知道应该走哪条路,所以我们需要尝试。尝试的过程就是一个函数。 我们选择了一个方向,后来发现又有一个多岔路口,这时候又需要进行一次选择。所以我们需要在上一次尝试结果的基础上,再做一次尝试,即在函数内部再调用一次函数,这就是递归的过程。 这样重复了若干次之后,发现这次选择的这条路走不通,这时候我们知道我们上一个路口选错了,所以我们要回到上一个路口重新选择其他路,这就是回溯的思想。
递归算法 (recursive algorithm)
在递归问题中,使用 JavaScript/Rust 做为示例,有几个经典的问题
数组求和
fibonacci 函数
JavaScript 中使用递归实现深拷贝
React-Router 递归实现配置 routes
Vue 中递归组件
经典的 fibonacci 函数示例
经典的 Fibonacci JavaScript 实现
exportdefaultfunctionfibonacci(n) {if (n < 0) thrownewError("输入的数字不能小于 0");if (n === 1 || n === 2) {return1;}returnfibonacci(n - 2) + fibonacci(n - 1);
}const fi = fibonacci(7);
console.log(fi);
复制代码经典的 Fibonacci Rust 实现(含测试)
fnmain() {println!("Hello, world!");letf1 = fibonacci(1);println!("{}", f1);letf2 = fibonacci(2);println!("{}", f2);letf3 = fibonacci(3);println!("{}", f3);letf4 = fibonacci(4);println!("{}", f4);
}pubfnfibonacci(n: i32) ->u32 {if n < 0 {panic!("输入的数字不能小于 0")};if n == 1 || n == 2 {return1}fibonacci(n - 2) + fibonacci(n - 1)
}#[cfg(test)]mod tests {use crate::fibonacci;#[test]fnfibonacci1() {letresult = fibonacci(1);assert_eq!(result, 1);}#[test]fnfibonacci2() {letresult = fibonacci(2);assert_eq!(result, 1);}#[test]fnfibonacci3() {letresult = fibonacci(3);assert_eq!(result, 2);}
}
复制代码从求和到递归
// 循环var sum = 0;
for (var i = 1; i <= 10; i++) {sum += i;
}
console.log(sum);// 递归functionsum(n) {if (n == 1) return1;returnsum(n - 1) + n;
}var amount = sum(10);
console.log(amount);
复制代码fnmain() {println!("Hello, world!");while_sum_fn();
}fnwhile_sum_fn() {letmut sum = 0;letmut i = 0;while i <= 10 {sum += i;i += 1;println!("sum: {}", sum);}println!("{sum}")
}
复制代码Rust for 循环与 js 中循环有很大的区别,此处 rust 使用 while 语句代替 JavaScript 中的 for 语句。
基础深拷贝
考虑:原始数据类型+引用数据类型
functiondeepClone(target) {const targetType = typeof target;if (targetType === "object" || targetType === "function") {let clone = Array.isArray(target) ? [] : {};for (const key in target) {clone[key] = deepClone(target[key]);}return clone;}return target;
}
复制代码问题:循环引用(通过内置 weakMap)
function deepClone(target, map = new Map()) {const targetType = typeof target;if (targetType === 'object' || targetType === 'function') {letclone = Array.isArray(target)?[]:{};if (map.get(target)) {return map.get(target);}map.set(target, clone);if(Object.prototype.toString.call(target) === '[object Date]'){clone = new Date(target)}if(Object.prototype.toString.call(target) === '[object Object]' ||Object.prototype.toString.call(target) === '[object Array]'){for (const key in target) {clone[key] = deepClone(target[key],map)}}return clone;}return target;
}
复制代码然后深拷贝需要考虑众多的 js 的数据类型(包括 es5+ 中新增的数据类型)。深拷贝缺点也非常明显,对于大对象,可能非常占用计算机资源。基于这个特点,React 社区针对 React 和 JavaScript 的诞生了不可变数据库:
immer
immutable.js
不可变数据,每次修改之后,会得到一个新的数据(但是尽可能的复用了原来的数据),这样弥补了深拷贝的数据时的性能问题。
react router 递归实现配置 route
// 递归函数constrotuerViews = (routerItems) => {if (routerItems && routerItems.length) {return routerItems.map(({ path, Component, children, redirect }) => {return children && children.length ? (<Routepath={path}key={path}element={<Suspensefallback={<Loading />}><Component /></Suspense>}>{rotuerViews(children)} // 递归遍历子路由{redirect ? (<Routepath={path}element={<Navigateto={redirect} />}></Route>) : (<Routepath={path}element={<Navigateto={children[0].path} />}></Route>)}</Route>) : (<Routekey={path}path={path}element={<Suspensefallback={<Loading />}><Component /></Suspense>}></Route>);});}
};
复制代码vue 中实现 tree 组件的递归(组件中如何使用自己)
<template><ul><li v-for="(item, index) in data" :key="index">{{ item.name }}<template v-if="item.children"><tree :data="item.children"></tree></template></li></ul>
</template><script>
export default {name: "tree",props: {data: {type: Array,default() {return [];},},},
};
</script>
复制代码扩展:尾部递归(Tail Recursion)
尾递归,首先要搞明白什么是尾部调用? 其实就是发生函数调用后,最后执行的语句是函数调用。尾递归,就是在函数最后(Tail)发生了函数的调用(但是调用的自己,就是尾部递归)。
尾递归在普通尾调用的基础上,多出了2个特征:
在尾部调用的是函数自身 (Self-called);
可通过优化,使得计算仅占用常量栈空间 (Stack Space)。
一个实例
functiontailFactorial(n, total) {if (n === 1) return total;returntailFactorial(n - 1, n * total);
}functionfactorial(n) {returntailFactorial(n, 1);
}factorial(5); // 120复制代码递归非常耗费内存,因为需要同时保存成千上百个调用记录,很容易发生"栈溢出"错误(stack overflow)。但对于尾递归来说,由于只存在一个调用记录,所以永远不会发生"栈溢出"错误。
尾部递归有哪些问题?
空间优化策略:尾递归
递归调用的缺点就是保存的调用栈(call frame),
如何优化尾部递归?
函数发生尾部递归的时候,返回的结果相差不大,保存在栈里面毫无意义。没有意义我们就应该不需要发生这些东西。所以计算机就可以省出一些内容。
递归展开
还是以阶乘为例:
functionfact(n) {if (n <= 0) {return1;} else {return n * fact(n - 1);}
}
复制代码6 * fact(5)
6 * (5 * fact(4))
6 * (5 * (4 * fact(3))))
6 * (5 * (4 * (3 * (2 * (1 * 1)))))) // <= 最终的展开复制代码展开的特点是:函数并没有真正的运行,需要较大的内存空间用于展开,如果内容过大就容易爆栈。
尾递归函数依然还是递归函数,如果不优化依然跟普通递归函数一样会爆栈,该展开多少层依旧是展开多少层。不会爆栈是因为语言的编译器或者解释器所做了“尾递归优化”,才让它不会爆栈的。
小结
什么是递归
从杨辉三角可是递推,到递归
递归与循环的区别
递归与回溯
递归算法常见的经典问题以及在前端 ReactRouter/Vue-Tree 中封装组件
尾递归及其优化、递归展开
大厂面试题分享 面试题库
后端面试题库 (面试必备) 推荐:★★★★★
地址:前端面试题库
相关文章:

【面试题】JavaScript中递归的理解
大厂面试题分享 面试题库后端面试题库 (面试必备) 推荐:★★★★★地址:前端面试题库递归 RecursionTo iterate is human, to recurse, divine. 理解迭代,神理解递归。本文会以 JavaScript为主、有部分 Rust 举例说明。…...
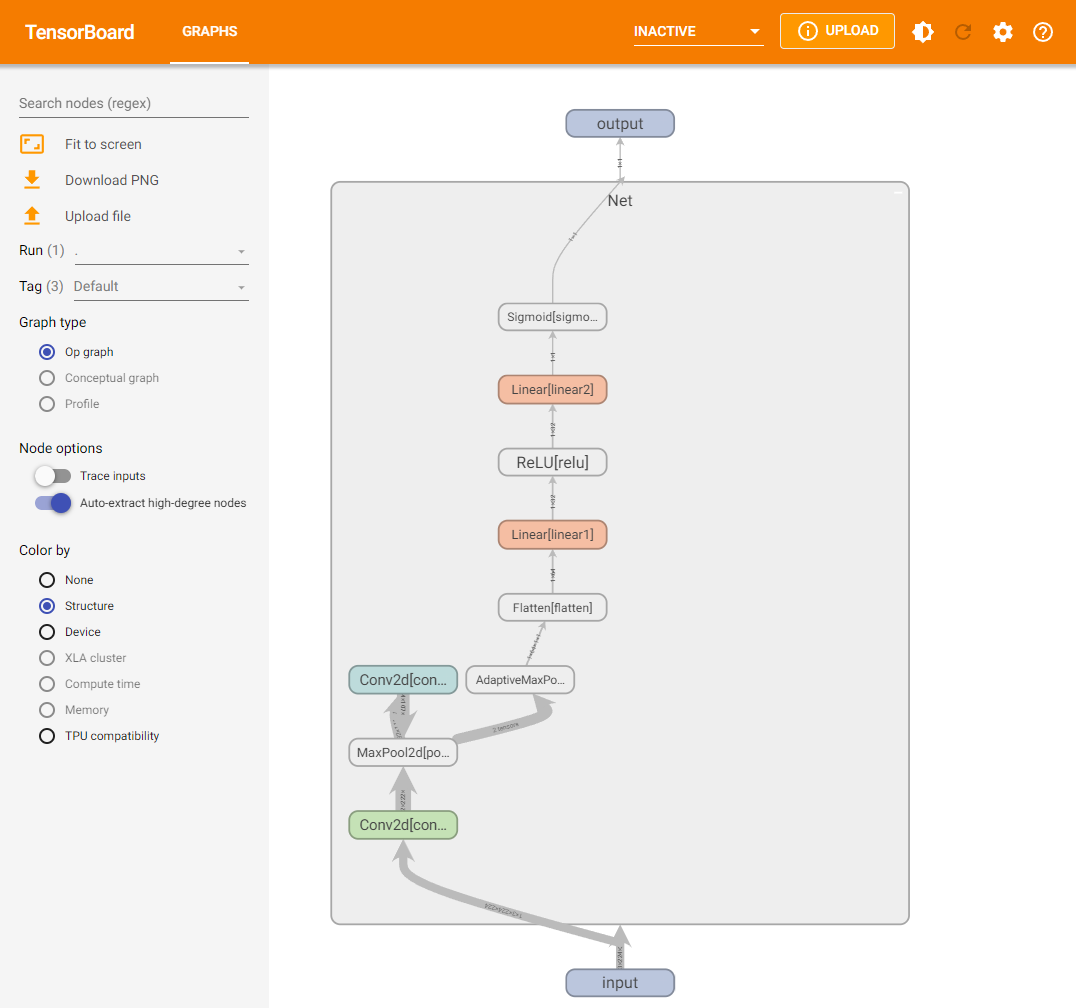
PyTorch学习笔记
PyTorch学习笔记(一):PyTorch环境安装 往期学习资料推荐: 1.Pytorch实战笔记_GoAI的博客-CSDN博客 2.Pytorch入门教程_GoAI的博客-CSDN博客 安装参考: 1.视频教程:3分钟深度学习【环境搭建】CUDA Anacon…...
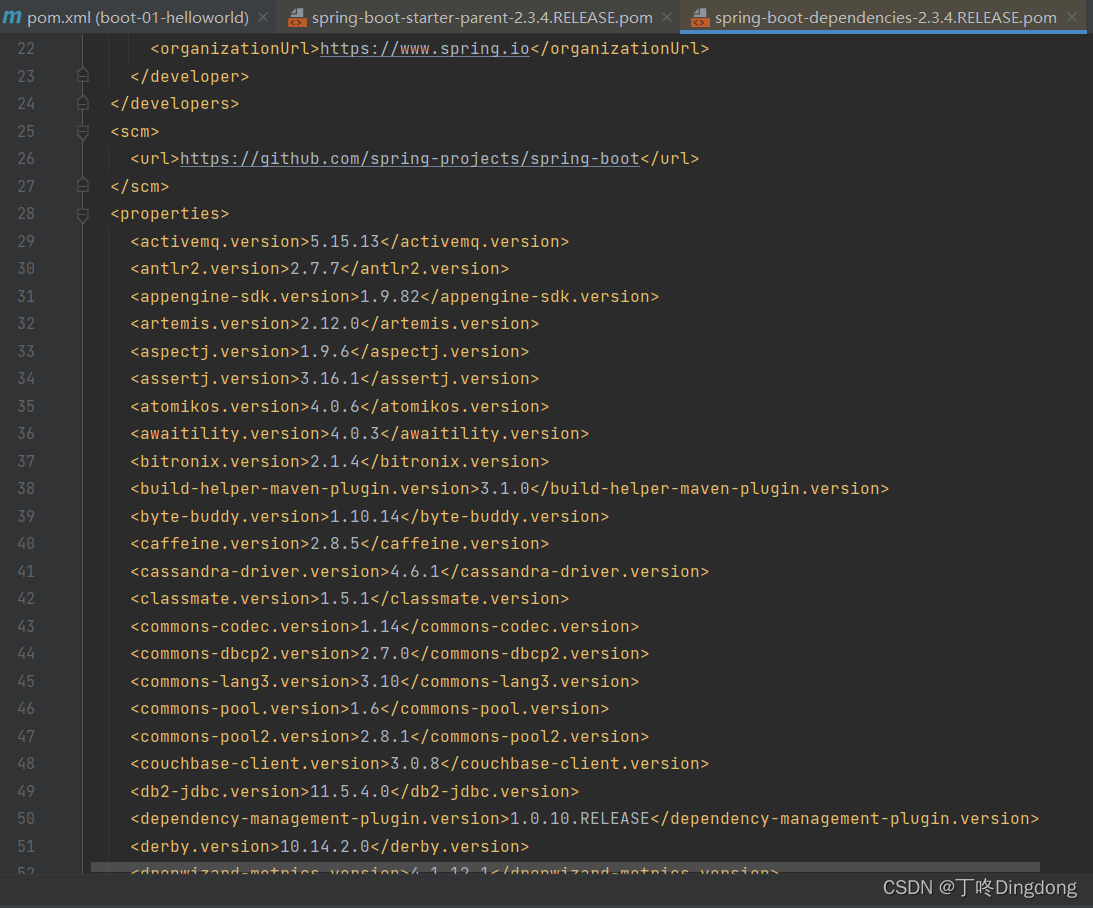
SpringBoot2知识点记录
SpringBoot2知识点记录1.SpringBoot2基础入门1.1 环境要求1.1.1 maven设置1.2 第一个程序 HelloWorld1.2.1 创建maven工程1.2.2 引入依赖1.2.3 创建主程序1.2.4 编写业务1.2.5 测试1.2.6 简化配置1.2.7 简化部署1.3 自动装配1.3.1 SpringBoot特点1.3.1.1 依赖管理1.3.1.2 自动装…...
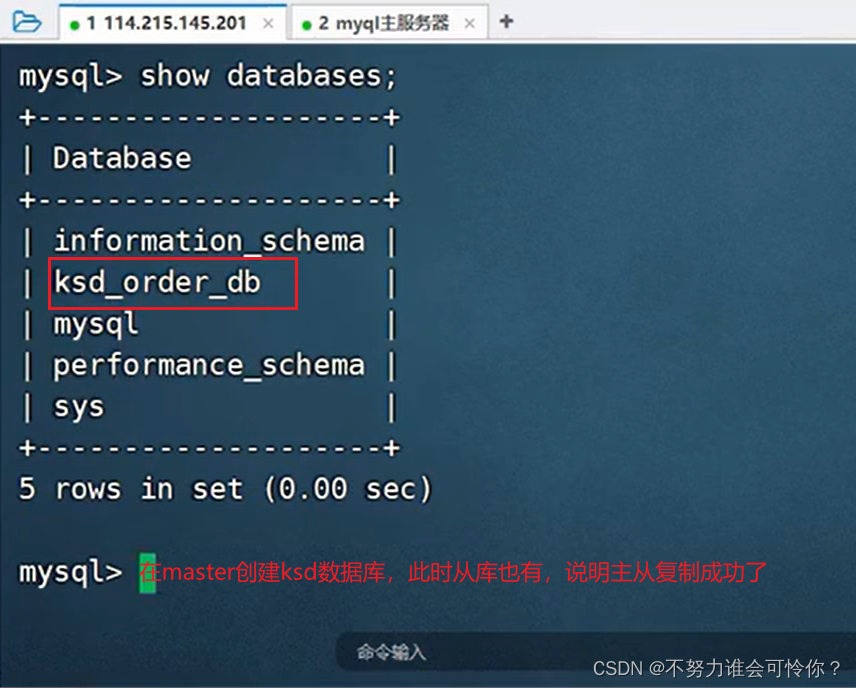
Mysql
1 Sql编写 count(*) //是对行数目进行计数 count(column_name) //是对列中不为空的行进行计数 SELECT COUNT( DISTINCT id ) FROM tablename; //计算表中id不同的记录有多少条 SELECT DISTINCT id, type FROM tablename; //返回表中id与type同时不同的结果 X.1 连表子查询 sel…...

Q4营收利润增长背后估值持续偏低,全球支付巨头PayPal前景如何?
作为国际版的“支付宝”,全球第三方支付巨头PayPal的业务横跨欧美市场,覆盖了全球200多个国家和地区。同时,PayPal也是首家进军中国支付市场的外资机构,实力强劲。然而,近两年,PayPal的市值一路从3000亿跌至…...
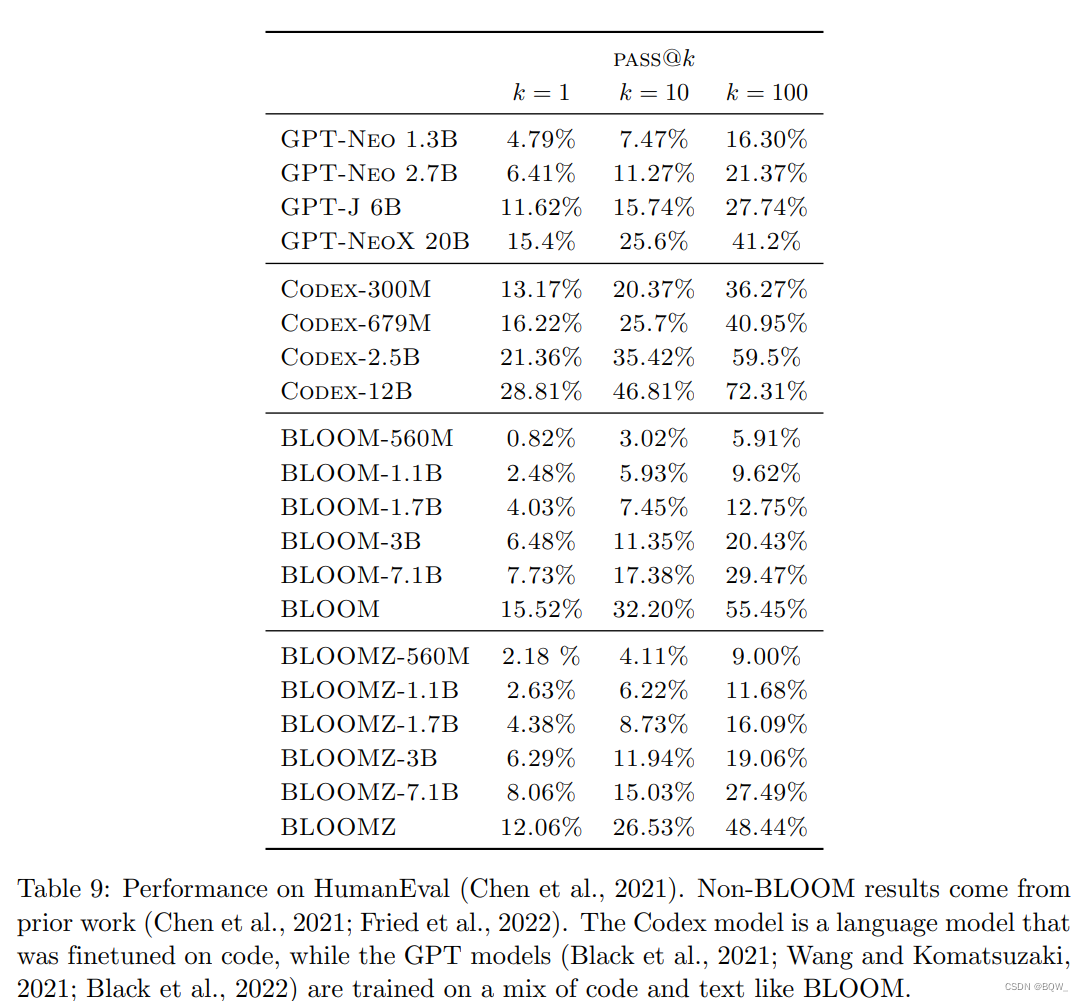
【自然语言处理】【大模型】BLOOM:一个176B参数且可开放获取的多语言模型
BLOOM:一个176B参数且可开放获取的多语言模型《BLOOM: A 176B-Parameter Open-Access Multilingual Language Model》论文地址:https://arxiv.org/pdf/2211.05100.pdf 相关博客 【自然语言处理】【大模型】用于大型Transformer的8-bit矩阵乘法介绍 【自然…...

小红书穿搭博主推广费用是多少?
小红书作为一个种草属性非常强的平台,商业价值是有目共睹的。很多爱美的女性都会在小红书上被种草某个商品,所以很多服装品牌都会在小红书上布局推广。 穿搭作为小红书的顶梁柱类目,刷小红书就能总是看到好看的穿搭博主分享美美的衣服&#…...
网络安全-PHPstudy环境搭建
网络安全-PHPstudy环境搭建 网络搭建我是专家,安全我懂的不多,所以可能很基础。。因为我自己都不懂,都是跟着课程学的 PHPstudy 这个东东是一个在windwos下可以快速部署的web开发环境,安装了就能用,也支持iis和ngin…...
)
operator的两种用法(重载和隐式类型转换)
文章目录重载隐式类型转换构造函数的隐式类型转换补充operator算子的隐式类型转换重载 略 隐式类型转换 构造函数的隐式类型转换 利用operator进行的隐式类型转换成为operator算子的隐式类型转换,讲这个之前先了解构造函数的隐式类型转换,请看以下代…...

vue常用指令
介绍 vue是以数据驱动和组件化开发为核心的前端框架,可以快速搭建前端应用 常用指令 指令:页面数据的操作(以数据去驱动DOM) <div v-xxx""></div>v-if:做元素的插入(append&…...
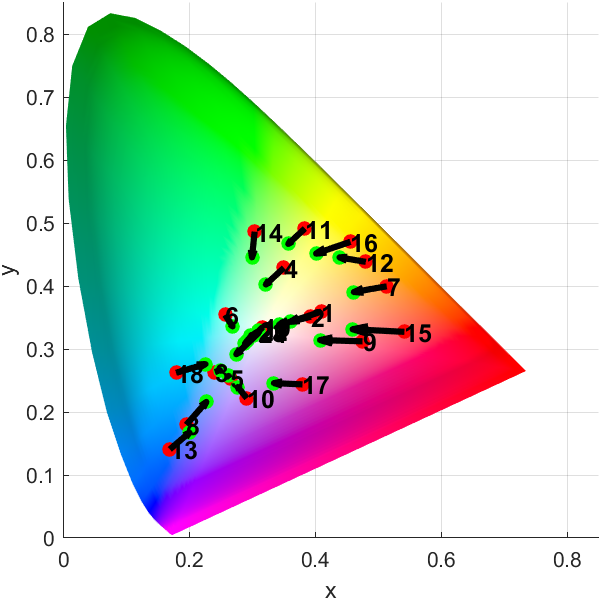
MATLAB | 有关数值矩阵、颜色图及颜色列表的技巧整理
这是一篇有关数值矩阵、颜色矩阵、颜色列表的技巧整合,会以随笔的形式想到哪写到哪,可能思绪会比较飘逸请大家见谅,本文大体分为以下几个部分: 数值矩阵用颜色显示从颜色矩阵提取颜色从颜色矩阵中提取数据颜色列表相关函数颜色测…...
)
C++模板元编程详细教程(之九)
前序文章请看: C模板元编程详细教程(之一) C模板元编程详细教程(之二) C模板元编程详细教程(之三) C模板元编程详细教程(之四) C模板元编程详细教程(之五&…...
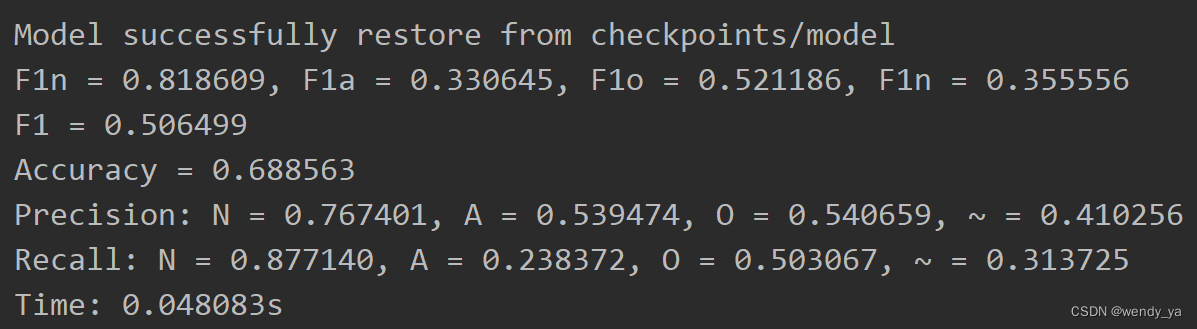
PhysioNet2017分类的代码实现
PhysioNet2017数据集介绍可参考文章:https://wendy.blog.csdn.net/article/details/128686196。本文主要介绍利用PhysioNet2017数据集对其进行分类的代码实现。 目录一、数据集预处理二、训练2.1 导入数据集并进行数据裁剪2.2 划分训练集、验证集和测试集2.3 设置训…...

正大期货本周财经大事抢先看
美国1月CPI、Fed 等央行官员谈话 美国1月超强劲的非农就业人口,让投资人开始上修对这波升息循环利率顶点的预测,也使本周二 (14 日) 的美国 1月 CPI 格外受关注。 介绍正大国际期货主账户对比国内期货的优势 第一点:权限都在主账户 例如…...

html+css综合练习一
文章目录一、小米注册页面1、要求2、案例图3、实现效果3.1、index.html3.2、style.css二、下午茶页面1、要求2、案例图3、index.html4、style.css三、法国巴黎页面1、要求2、案例图3、index.html4、style.css一、小米注册页面 1、要求 阅读下列说明、效果图,进行静…...
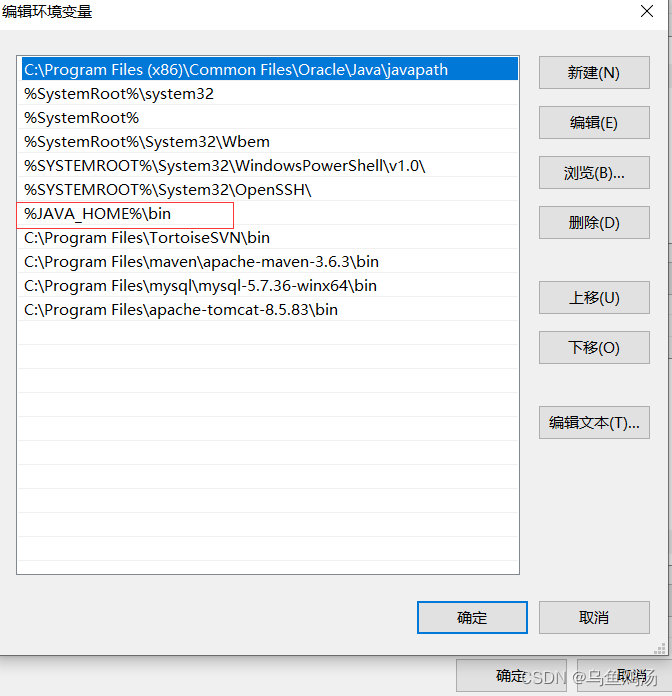
安装jdk8
目录标题一、下载地址(一)Linux下载(二)Win下载二、安装(一)Linux(二)Win三、卸载(一)Linux(二)Win一、下载地址 jdk8最新版 jdk8其他…...

二分法心得
原教程见labuladong 首先,我们建议左右区间全部用闭区间。那么第一个搜索区间:left0; rightlen-1; 进入while循环,结束条件是right<left。 然后求mid,如果nums[mid]的值比target大,说明target在左边,…...

Linux安装Docker完整教程
背景最近接手了几个项目,发现项目的部署基本上都是基于Docker的,幸亏在几年前已经熟悉的Docker的基本使用,没有抓瞎。这两年随着云原生的发展,Docker在云原生中的作用使得它也蓬勃发展起来。今天这篇文章就带大家一起实现一下在Li…...

备份基础知识
备份策略可包括:– 整个数据库(整个)– 部分数据库(部分)• 备份类型可指示包含以下项:– 所选文件中的所有数据块(完全备份)– 只限自以前某次备份以来更改过的信息(增量…...

C++学习记录——팔 内存管理
文章目录1、动态内存管理2、内存管理方式operator new operator delete3、new和delete的实现原理1、动态内存管理 C兼容C语言关于内存分配的语法,而添加了C独有的东西。 //int* p1 (int*)malloc(sizeof(int));int* p1 new int;new是一个操作符,C不再需…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

通过 Ansible 在 Windows 2022 上安装 IIS Web 服务器
拓扑结构 这是一个用于通过 Ansible 部署 IIS Web 服务器的实验室拓扑。 前提条件: 在被管理的节点上安装WinRm 准备一张自签名的证书 开放防火墙入站tcp 5985 5986端口 准备自签名证书 PS C:\Users\azureuser> $cert New-SelfSignedCertificate -DnsName &…...

第八部分:阶段项目 6:构建 React 前端应用
现在,是时候将你学到的 React 基础知识付诸实践,构建一个简单的前端应用来模拟与后端 API 的交互了。在这个阶段,你可以先使用模拟数据,或者如果你的后端 API(阶段项目 5)已经搭建好,可以直接连…...

CppCon 2015 学习:Time Programming Fundamentals
Civil Time 公历时间 特点: 共 6 个字段: Year(年)Month(月)Day(日)Hour(小时)Minute(分钟)Second(秒) 表示…...

leetcode_69.x的平方根
题目如下 : 看到题 ,我们最原始的想法就是暴力解决: for(long long i 0;i<INT_MAX;i){if(i*ix){return i;}else if((i*i>x)&&((i-1)*(i-1)<x)){return i-1;}}我们直接开始遍历,我们是整数的平方根,所以我们分两…...
