神经网络激活函数
神经网络激活函数
- 神经网络激活函数的定义
- 为什么神经网络要用激活函数
- 神经网络激活函数的求导
- Sigmoid激活函数
- Tanh激活函数
- Softmax激活函数
神经网络激活函数的定义
所谓激活函数(Activation Function),就是在人工神经网络的神经元上运行的函数,负责将神经元的输入映射到输出端。
激活函数(Activation functions)对于人工神经网络模型去学习、理解非常复杂和非线性的函数来说具有十分重要的作用。它们将非线性特性引入到我们的网络中。如图:
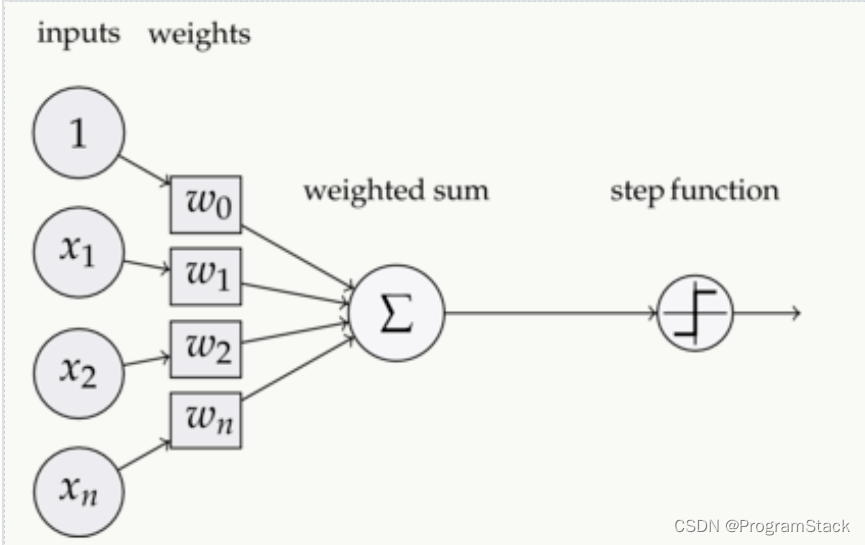
在神经元中,输入的 inputs 通过加权,求和后,还被作用了一个函数,这个函数就是激活函数。引入激活函数是为了增加神经网络模型的非线性。没有激活函数的每层都相当于矩阵相乘。就算你叠加了若干层之后,无非还是个矩阵相乘罢了。
为什么神经网络要用激活函数
如果不用激活函数,每一层输出都是上层输入的线性函数,无论神经网络有多少层,输出都是输入的线性组合,这种情况就是最原始的感知机(Perceptron)。
如果使用的话,激活函数给神经元引入了非线性因素,使得神经网络可以任意逼近任何非线性函数,这样神经网络就可以应用到众多的非线性模型中。
神经网络激活函数的求导
对神经网络激活函数求导有一个特性,它的导函数始终都可以用原式表示出来,下面列举常用神经网络激活函数:
Sigmoid激活函数
表达式为:σ(x)=11+e−x\sigma (x) = \frac{1}{1+e^{-x}}σ(x)=1+e−x1
函数图像如下:
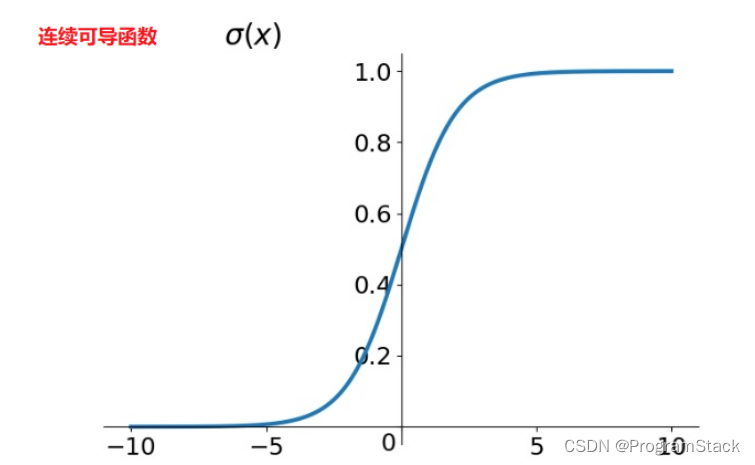
其导函数:σ′(x)=∂∂x11+e−x=11+e−x∗(1−11+e−x)=σ(x)∗(1−σ(x))\sigma'(x) = \frac{\partial}{\partial x}\frac{1}{1+e^{-x}} = \frac{1}{1+e^{-x}}*(1-\frac{1}{1+e^{-x}})=\sigma(x)*(1-\sigma(x))σ′(x)=∂x∂1+e−x1=1+e−x1∗(1−1+e−x1)=σ(x)∗(1−σ(x))
Tanh激活函数
表达式为:tanh(x)=ex−e−xex+e−x=21+e−2x−1tanh(x) = \frac{e^x-e^{-x}}{e^x+e^{-x}}=\frac{2}{1+e^{-2x}}-1tanh(x)=ex+e−xex−e−x=1+e−2x2−1
而我们的Sigma激活函数表达式为σ(x)=11+e−x\sigma (x) = \frac{1}{1+e^{-x}}σ(x)=1+e−x1,所以Tanh激活函数可以用Sigma激活函数表示,即tanh(x)=2σ(2x)−1tanh(x) = 2\sigma(2x)-1tanh(x)=2σ(2x)−1
Tanh 函数可以看作是放大并平移的 Sigmoid 函数,但因为是零中心化的 (zero-centered) ,通常收敛速度快于 Sigmoid 函数,下图是二者的对比:
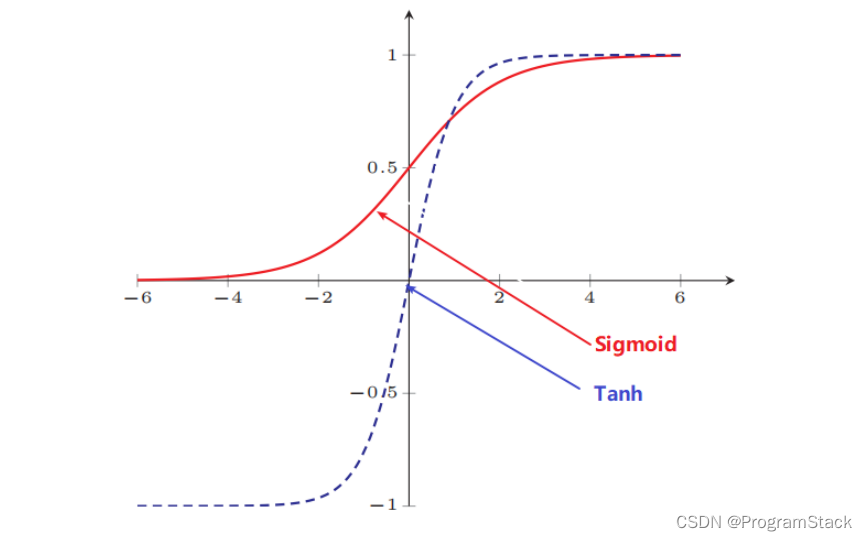
其导函数:tanh′(x)=(ex+e−x)2−(ex−e−x)2(ex+e−x)2=1−(ex−e−x)2(ex+e−x)2=1−tanh(x)2tanh'(x) = \frac{(e^x+e^{-x})^2-(e^x-e^{-x})^2}{(e^x+e^{-x})^2}= 1- \frac{(e^x-e^{-x})^2}{(e^x+e^{-x})^2}=1-tanh(x)^2tanh′(x)=(ex+e−x)2(ex+e−x)2−(ex−e−x)2=1−(ex+e−x)2(ex−e−x)2=1−tanh(x)2
Softmax激活函数
表达式:yi=softmax(zi)=ezi∑j=1Cezjy_i = softmax(z_i) = \frac{e^{z_i}}{\sum_{j=1}^Ce^{zj}}yi=softmax(zi)=∑j=1Cezjezi
Softmax函数将多个标量映射为一个概率分布,yiy_iyi表示第i个输出值,即属于类别iii的概率,所有类别概率加起来为1,即∑i=1Cyi=1\sum_{i = 1}^Cy_i = 1∑i=1Cyi=1,其中z=WTxz = W^Txz=WTx,表示线性方程,图中的ziz_izi表示zzz的第i个元素的值。Softmax函数用于多分类,会对应多个方程。
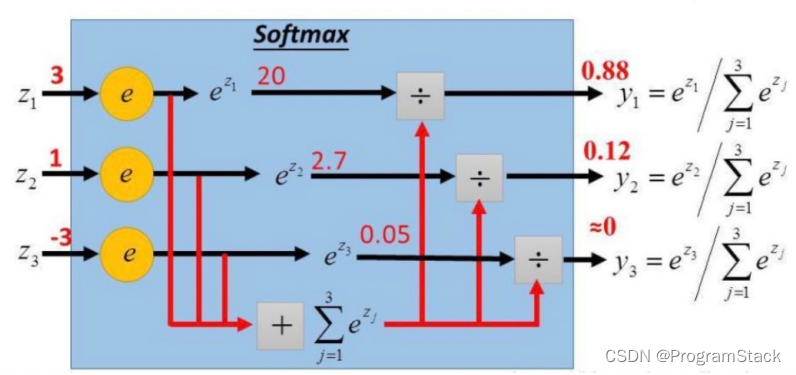
首先求标量形式的导数,即第i个输出对于第j个输入的偏导数
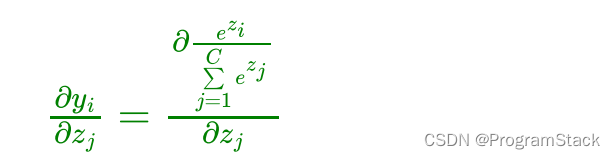
其导函数:
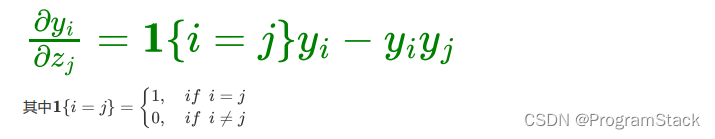
这里就不在做过多的推导了,感兴趣的小伙伴可以去翻阅书籍哦
相关文章:
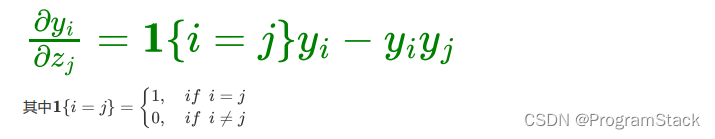
神经网络激活函数
神经网络激活函数神经网络激活函数的定义为什么神经网络要用激活函数神经网络激活函数的求导Sigmoid激活函数Tanh激活函数Softmax激活函数神经网络激活函数的定义 所谓激活函数(Activation Function),就是在人工神经网络的神经元上运行的函数…...

2.C 语言基本语法
文章目录二、C 语言基本语法1.语句2.表达式3.语句块4.空格5.注释6.printf()函数基本用法7.占位符8.输出格式10.标准库,头文件提示:以下是本篇文章正文内容,下面案例可供参考 二、C 语言基本语法 1.语句 C语言的代码由一行行语句࿰…...

Qt 6.5 LTS 正式发布
Qt 6.5 LTS 已正式发布。此版本为图形和 UI 开发者以及应用程序后端引入了许多新功能,还包含许多修复和通用的改进。Qt 6.5 将成为商业许可证持有者的长期支持 (LTS) 版本。 部分更新亮点: 改进主题和样式 使用 Qt 6.5,应用程序能够便捷地支持…...

Linux权限提升—定时任务、环境变量、权限配置不当、数据库等提权
Linux权限提升—定时任务、环境变量、权限配置不当、数据库等提权1. 前言1.1. 如何找编译好的EXP2. 定时任务提权2.1. 查看定时任务2.2. 通配符注入提权2.2.1. 创建执行脚本2.2.2. 创建定时任务2.2.3. 查看效果2.2.4. 提权操作2.2.4.1. 切换普通用户2.2.4.2. 执行命令2.2.4.3. …...

Python爬虫——使用requests和beautifulsoup4库来爬取指定网页的信息
以下是一个简单的Python代码,使用requests和beautifulsoup4库来爬取指定网页的信息: import requests from bs4 import BeautifulSoupurl "https://example.com"# 发送GET请求,获取网页内容 response requests.get(url)# 将网页内…...
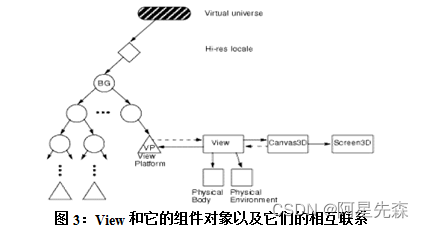
基于Java3D的网络三维技术的设计与实现
3D图形技术并不是一个新话题,在图形工作站以至于PC机上早已日臻成熟,并已应用到各个领域。然而互联网的出现,却使3D图形技术发生了和正在发生着微妙而深刻的变化。Web3D协会(前身是VRML协会)最先使用Web3D术语…...
python机器学习数据建模与分析——数据预测与预测建模
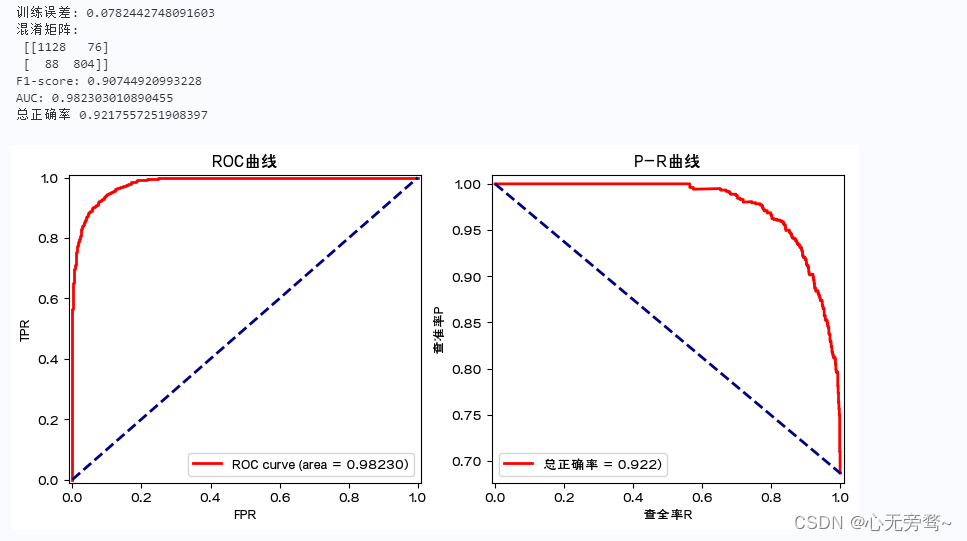
文章目录前言一、预测建模1.1 预测建模涉及的方面:1.2 预测建模的几何理解1.3 预测模型参数估计的基本策略1.4 有监督学习算法与损失函数:1.5 参数解空间和搜索策略1.6 预测模型的评价1.6.1 模型误差的评价指标1.6.2 模型的图形化评价工具1.6.3 训练误差…...

Flink系列-6、Flink DataSet的Transformation
版权声明:本文为博主原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接和本声明。 大数据系列文章目录 官方网址:https://flink.apache.org/ 学习资料:https://flink-learning.org.cn/ 目录Flink 算子Ma…...

Java-类的知识进阶
Java类的知识进阶 类的继承(扩张类) Java类的继承是指一个类可以继承另一个类的属性和方法,从而使得子类可以重用父类的代码。继承是面向对象编程中的重要概念,它可以帮助我们避免重复编写代码,提高代码的复用性和可…...
摘要算法)
C# | 上位机开发新手指南(六)摘要算法
C# | 上位机开发新手指南(六)摘要算法 文章目录C# | 上位机开发新手指南(六)摘要算法前言常见摘要算法源码MD5算法SHA-1算法SHA-256算法SHA-512算法BLAKE2算法RIPEMD算法Whirlpool算法前言 你知道摘要算法么?它在保障…...

测试工程师:“ 这锅我不背 ” ,面对灵魂三问,如何回怼?
前言 在一个周末的早餐我被同事小周叫出去跑步,本想睡个懒觉,但是看他情绪不太稳定的样子,无奈艰难爬起陪他去跑步。 只见她气冲冲的对着河边大喊:真是冤枉啊!!! 原来是在工作中被莫名其妙背锅࿰…...
【Java闭关修炼】SpringBoot-SpringMVC概述和入门
SpringMVC概述和入门 MVC概述 实体类Bean:专门 存储业务数据 Student User业务处理Bean:指的是Service或者Dao 专门用来处理业务逻辑或者数据访问 用户通过视图层发送请求到服务器,在服务器中请求被Controller接受,Controller调用相应的MOdel层处理请求…...

pdf转换器免费版哪种好用:Aiseesoft PDF Converter Ultimate | 无损转word转Excel转PPT转图片啥都行!!!
Aiseesoft PDF Converter Ultimate 是一款优秀且高效可靠的无损电脑免费版pdf转换器软件,凭借卓越高识别精度的强悍OCR识别技术,可精准识别英文、法文、中文、德文、日文、韩文、意大利文、土耳其文等190多个国家的语言以及各种公式和编程语言࿰…...

革新市场营销,突破瓶颈:关键词采集和市场调查的秘密武器
近年来,全球新兴行业不断涌现,其中一些行业甚至成为了热门话题。这些新兴行业的出现,不仅带来了新的商机和发展机遇,也对传统产业带来了冲击和挑战。对于那些想要进入新兴行业的人来说,了解这些行业的关键词和市场情况…...
3年测试经验只会“点点点”,不会自动化即将面临公司淘汰?沉淀100天继续做测试
前段时间一个朋友跟我吐槽,说自己做软件测试工作已经3年了,可这三年自己的能力并没有得到提升,反而随着互联网的发展,自己只会“点点点”的技能即将被淘汰。说自己很苦恼了,想要提升一下自己,可不知道该如何…...
python:异常处理与文件操作(知识点详解+代码展示)
文章目录一、异常处理1、try...except语句2、finally语句二、断言1、定义2、举例例一:例二:三、文件操作1、写文件操作2、读文件操作学习目标:1、掌握异常处理的方法2、掌握断言的使用3、掌握打开文件、读文件和写文件的方法一、异常处理 引…...
)
SpringBoot 过滤器和拦截器(三十八)
我喜欢你,可是你却并不知道. 上一章简单介绍了SpringBoot参数验证(三十七) ,如果没有看过,请观看上一章 关于过滤器和拦截器已经讲很多了, 这里老蝴蝶只说一下 SpringBoot 的用法。 可以看之前的文章: https://blog.csdn.net/yjltx1234csdn/article/d…...

Memcache论文总结——Lec16
文章目录一、相关名词1.mcrouter层2.GUTTER SERVER3.mcsqueal4.remote mark二、当流量增长了如何SCALE 你的网站?三、背景及业务特点1.读多写少2.FB需求:3.之前情况四、简介五、FaceBook的架构五、Cache Policy六、In a Cluster : Latency and Load(一&a…...
父子组件传值问题
文章目录前言一、问题描述二、问题解决前言 在写毕业设计,涉及了一些前端Vue.js的组件传值知识并出现了相关问题,因此进行记录。 问题 Vue.js的使用不熟练,相关组件、props等掌握不清晰前端代码书写不规范 望指正! 一、问题描述 …...

Redis大key问题
Redis大key问题 什么是big key? bigKey的危害: 大key不仅仅是占用内存而已,如果是仅仅内存的问题 那么扩大内存就好了。禁止大key是主要是因为你操作redis,比如说读/写等操作redis的时候 会有io操作,大key会导致io操作…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

LangChain知识库管理后端接口:数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块,用于对本地知识库系统中的知识库进行增删改查(CRUD)操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...
