leetcode剑指 Offer 16. 数值的整数次方
- 题目描述
- 解题思路
- 执行结果
题目描述
实现 pow(x, n) ,即计算 x 的 n 次幂函数(即,xn)。不得使用库函数,同时不需要考虑大数问题。
示例 1:
输入:x = 2.00000, n = 10 输出:1024.00000 示例 2:
输入:x = 2.10000, n = 3 输出:9.26100 示例 3:
输入:x = 2.00000, n = -2 输出:0.25000 解释:2-2 = 1/22 = 1/4 = 0.25
提示:
-100.0 < x < 100.0 -231 <= n <= 231-1 -104 <= xn <= 104
来源:力扣(LeetCode) 链接:https://leetcode.cn/problems/shu-zhi-de-zheng-shu-ci-fang-lcof 著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
解题思路
计算x^n
法1
循环相乘
r*=x循环n次
时间复杂度(O(n)) 空间复杂度(O(1))
法2
快速幂\
举个例子n^4=n^2*n^2 n^8=n^4*n^4 这样我们可以减少循环的次数只需要计算n^2,n^4...n^2^m就行了 比如x^10=x^8*x^2,我们只需要计算到x^8就可以了,
具体实现过程
令一个中间变量t=x
t*=t
当n&1==1时执行
r*=t
循环执行n>>1直到n==0为止\
时间复杂度(O(logn)) 空间复杂度(O(1))
法3
时间复杂度(O()) 空间复杂度(O())
执行结果
快速幂
快速幂算法
// 快速幂
func myPow(x float64, n int) (r float64) {
if n < 0 {//当n为负数的时候,我们将x=x^-1进行计算就不用定义新的计算方法了
x = 1 / x
n = -n
}
r = 1
for t := x; n > 0; {
if n&1 == 1 {
r *= t//当为1时计算入值
}
t *= t//幂的叠加
n >>= 1
}
return
}
执行结果: 通过 显示详情 查看示例代码 添加备注
执行用时: 0 ms , 在所有 Go 提交中击败了 100.00% 的用户 内存消耗: 1.9 MB , 在所有 Go 提交中击败了 100.00% 的用户 通过测试用例: 304 / 304
本文由 mdnice 多平台发布
相关文章:

leetcode剑指 Offer 16. 数值的整数次方
题目描述解题思路执行结果leetcode .题目描述 实现 pow(x, n) ,即计算 x 的 n 次幂函数(即,xn)。不得使用库函数,同时不需要考虑大数问题。 示例 1: 输入:x 2.00000, n 10 输出:1…...
漏洞挖掘相关-信息收集
一、常见端口以及漏洞 1.FTP:文件传输协议 TCP端口20、21,20用于传输数据,21用于传输控制信息 (1) ftp基础爆破: owasp的Bruter,hydra以及msf中的ftp爆破模块。 (2) ftp匿名访问:用户名: anonymous密码:为空或者任意邮箱 (3) vsftpd后门: …...

海外分支如何加速访问国内总部办公系统?海域网发布 Sea-WAN解决方案
近年来,一大批优秀的中国企业走向世界,品牌越来越响亮,海外影响力越来越大,比如名创优品,国货之光“花西子”,安科创新等,很多企业在海外设立分支机构为当地客户服务,与此同时&#…...

js设计模式——责任链模式
一、概述 责任链是一种行为设计模式,它允许将请求沿着处理链传递,直到有一个处理器可以处理该请求。在这种模式中,每个处理器都有机会处理请求,如果没有一个处理器能够处理请求,那么请求最终将被忽略。这种模式可以帮…...

接口组成更新
接口组成更新概述: 接口的组成: 常量 public static final 抽象方法 public abstract 默认方法java8 静态方法java8 私有方法java9 接口中默认方法 接口中默认方法的定义格式: 格式:public default 返回值类型 方法名&#x…...
int(1) 和 int(10)区别
有个表的要加个user_id字段,user_id字段可能很大, alter table xxx ADD user_id int(1)。 int(1)怕是不够用吧,接下来是一通解释。 我们知道在mysql中 int占4个字节,那么对于无符号的int,最大值是2^32-1 4294967295&a…...

华为OD机试-组合出合法最小数-2022Q4 A卷-Py/Java/JS
给一个数组,数组里面都是代表非负整数的字符串,将数组里所有的数值排列组合拼接起来组成一个数字,输出拼成的最小的数字。 输入描述 一个数组,数组不为空,数组里面都是代表非负整数的字符串,可以是0开头,例如:[”13","045","09","56&qu…...
ChatGPT中文在线官网-如何与chat GPT对话
怎么下载ChatGPT中文版 ChatGPT是一种基于Transformer架构的自然语言处理技术,其中包含了多个预训练的中文语言模型。这些中文ChatGPT模型大多数发布在Github上,可以通过Github的源码库来下载并使用,包括以下几种方式: 下载预训练…...
macOS 13.3.1 (22E261)With OpenCore 0.9.2开发版 and winPE双引导分区原版镜像
镜像特点 原文来源于黑果魏叔官网,转载需注明出处。(下载请直接百度黑果魏叔) 完全由黑果魏叔官方制作,针对各种机型进行默认配置,让黑苹果安装不再困难。系统镜像设置为双引导分区,全面去除clover引导分…...

《iTOP-3568开发板快速测试手册》第7章 Yocto系统外设功能测试(1)
瑞芯微RK3568芯片是一款定位中高端的通用型SOC,采用22nm制程工艺,搭载一颗四核Cortex-A55处理器和Mali G52 2EE 图形处理器。RK3568 支持4K 解码和 1080P 编码,支持SATA/PCIE/USB3.0 外围接口。RK3568内置独立NPU,可用于轻量级人工…...

【周末闲谈】AI的旅途
个人主页:【😊个人主页】 系列专栏:【❤️周末闲谈】 系列目录 ✨第一周 二进制VS三进制 ✨第二周 文心一言,模仿还是超越? ✨第二周 畅想AR 文章目录系列目录前言AIAI的开端第一个AI程序AI的寒冬关于AI的思考末尾前言…...

回溯算法--01背包问题
目录 回溯算法--01背包问题 [算法描述] [回溯法基本思想] 法一: 法二: 代码: 运行结果 代码改进 回溯算法--01背包问题 [算法描述] 0-1背包问题是子集选取问题。一般情况下,0-1背包问题是NP完全问题。0-1背包问题的解空…...
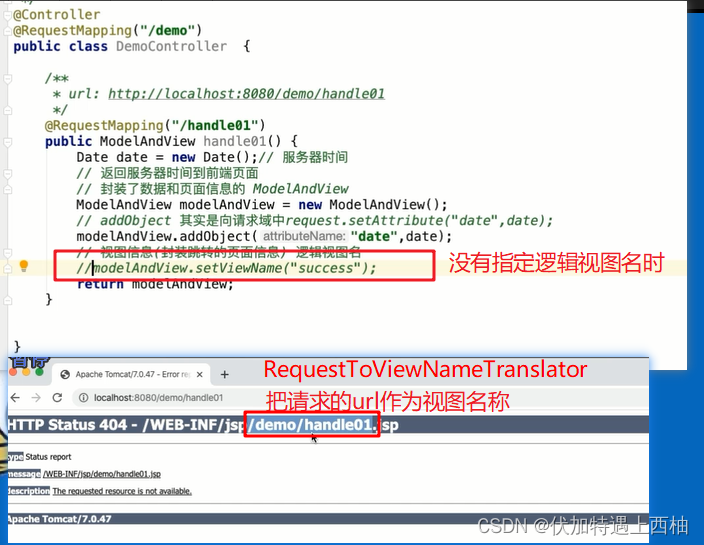
Spring MVC请求处理流程分析
Spring MVC请求处理流程分析一 Spring MVC 请求处理流程二 Spring MVC 请求处理流程源码分析2.1架构图解2.2 重要时机点分析2.3核心步骤分析2.3.1 getHandler⽅法剖析2.3.2 getHandlerAdapter⽅法剖析2.3.3 ha.handle⽅法剖析2.3.4 processDispatchResult⽅法剖析三 Spring MVC…...

Python高阶知识之属性管理
本文主要介绍Python高阶知识中的属性管理,这部分知识在常规Python编程中用的很少,但对于想深度了解Python甚至有志于自己编写实用框架的人,还是很有必要的,并且如果掌握了,对日常的代码学习等也会有一定好处。 本文结…...
【Linux】创建目录文件,并完成删除,拷贝,移动,比较等操作
操作前: 1.创建目录 mkdir命令 格式: mkdir 目录名 示例: 点击主文件夹查看 2.创建文件夹 touch命令 格式: touch 文件夹名 示例: 3.重命名文件 mv命令 格式 : mv 123.txt abc.txt 示…...

python http服务搭建教程
作为互联网时代的基础技术之一, HTTP是一个简单的 HTTP协议,它包含了请求、应答和超文本传输控制等机制。HTTP协议由 TCP/IP协议族定义,其中包括了三个基本的服务:发送、接收、存储。客户端和服务器之间传输信息时,数据…...

高速数字信号VS射频信号,到底哪个更难设计?
一博高速先生成员:黄刚熟悉高速先生的小伙伴们会知道,我们是以研究高速数字信号为主的团队,从不到1G到目前在研究的112G,高速先生就这样一直研究过来的,分享的案例也大多是以高速数字信号为主的案例。最近受到我们粉丝…...

相对路径读取json文件 labelme_shapes_to_label 标签
直接读取: import jsonwith open(file.json, r, encodingutf-8) as f:data json.load(f) 忽略错误读取: import jsonimport codecs with codecs.open(file.json, r, encodingutf-8, errorsignore) as f:data json.load(f) labelme_shapes_to_labe…...
IDEA工具避坑指南(十一):git导入SpringBoot后|不识别依赖 |大量爆红 | 无法启动
一、前言 使用在IDEA2019中,使用Git工具导入SpringBoot项目后,java类的依赖包大量爆红、不能启动SpringBoot,不能自动识别启动类。 提示:如果刚拉取的项目,只有.git和.idea文件,没有src或java目录ÿ…...
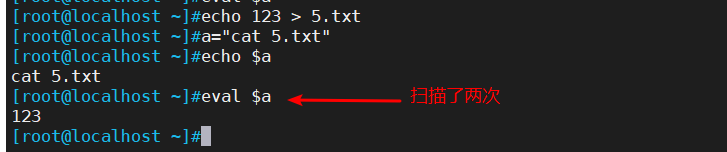
管道命令(sort、uniq、tr、cut、eval命令)
一、sort命令 1、作用 以行为单位对文件内容进行排序也可以根据不同的数据类型来排序 2、语法格式 sort [选项] 参数cat file | sort 选项3、常用选项 -f∶ 忽略大小写,会将小写字母都转换为大写字母来进行比较; -b∶ 忽略每行前面的空格;…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...
