回溯算法--01背包问题
目录
回溯算法--01背包问题
[算法描述]
[回溯法基本思想]
法一:
法二:
代码:
运行结果
代码改进
回溯算法--01背包问题
[算法描述]
0-1背包问题是子集选取问题。一般情况下,0-1背包问题是NP完全问题。0-1背包问题的解空间可以用子集树表示。解0-1背包问题的回溯法与解装载问题的回溯法十分相似。在搜索解空间树时,只要其左儿子节点是一个可行的节点,搜索就进入其左子树;而当右子树中有可能包含最优解时才进入右子树搜索,否则将右子树剪去。设r是当前剩余物品价值总和;cp是当前价值;bestp是当前最优价值。当cp+r<=bestp时,可剪去右子树。计算右子树中解的上界的更好的办法是,将剩余物品依其单位重量价值排序,然后依次装入物品,直至装不下时,再装入该物品的一部分而装满背包,由此得到的价值是右子树的上界。
0--1背包的一个实例:
n=3, c=50,
w={10,30,20},
v(p)={60,120,100}的
0-1背包问题的最优解和最优值。<w为重量,v为价值量,n为物品个数,c为背包容量>
[回溯法基本思想]
确定了解空间的组织结构后,【回溯法从开始节点(根节点)出发,以深度优先搜索整个解空间。这个开始的节点为活节点,同时成为当前的扩展节点。在当前的扩展节点处,搜素向纵深方向移至一个新节点。这个新节点就成为新的活节点,并成为当前扩展节点。如果当前节点处不能再向纵深方向移动,则当前扩展节点为死节点。此时,应往回移动到最近的一个活节点处。回溯法以这种方式递归的在解空间中搜素,直至找到所有符合要求的解或解空间中已无活节点。】(即深度优先搜索)
【优化方法】
剪枝(一):当前决策放入的物品总重量已经大于背包容量时,没有必要继续决策,此时可以将其左子树剪掉。
剪枝(二):如果将当前扩展节点后剩下的所有物品都装入还没有目前已求得的最优值大的话,就不在进行决策了,直接返回。
递归回溯时,在当前扩展节点处会通过设置约束函数和限界函数。不满足条件的,剪去相应的子树
【0-1背包算法分析】
对于0-1背包问题,可用一颗完全二叉树表示其解空间,针对上述实例(n=5),解空间树有32个可能的解,解空间树如下图所示。
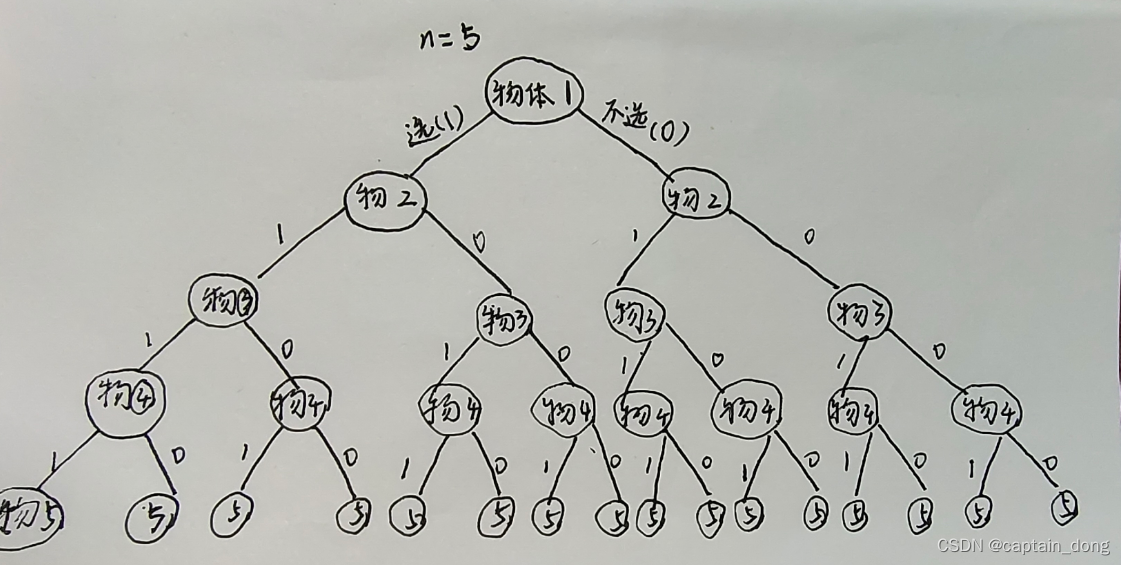
法一:
回溯算法是一种解决问题的通用算法,能够在一个问题的所有解空间中,按深度优先的策略搜索,直到找到所需要的解或者搜索完整个解空间都没有找到解。0-1背包问题是指在限制背包容量的情况下,在一堆物品中选择一部分,使得这些物品的总价值最大。
C++ 设计回溯算法解决 0-1 背包问题的思路如下:
- 定义一个全局数组 max_value,用于存储当前找到的最大总价值;
- 定义一个局部数组 current_weight,用于存储当前已选物品的总重量;
- 定义一个递归函数 backpack,用于搜索某一层的所有可能性;
- 在 backpack 函数中,首先判断是否已经遍历完所有物品,如果是则更新数组 max_value;
- 如果还没有处理完所有物品,则需要对当前物品进行判断。如果当前物品的重量加上当前已选物品的总重量仍然小于等于背包容量,则将当前物品加入已选物品中,并进入下一层搜索。否则,不加入当前物品,并进入下一层搜索。
- 在递归返回后,需要将当前物品从已选物品中删除,以方便下一次搜索。
一个简单的 C++ 回溯算法解决 0-1 背包问题的示例代码如下:
/*
* 回溯算法---0-1背包问题
*/
#include <iostream>
using namespace std;const int max_n = 10;
const int capacity = 50;int w[] = { 10, 20, 30, 40, 50, 60, 70, 80, 90, 100 }; // 物品重量数组
int v[] = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 }; // 物品价值数组
bool selected[max_n]; // 记录物品是否被选择
int current_weight = 0; // 当前已选物品的总重量
int max_value = 0; // 已找到的最大总价值// backpack 函数用于搜索某一层的所有可能性
void backpack(int i) {if (i == max_n) { // 如果已经遍历完所有物品,则更新 max_valueif (current_weight <= capacity && max_value < v[i]) {max_value = v[i];}return;}if (current_weight + w[i] <= capacity) { // 如果能将当前物品加入背包selected[i] = true;current_weight += w[i];backpack(i + 1); // 进入下一层current_weight -= w[i]; // 递归返回后,需要将当前物品从已选物品中删除selected[i] = false;}backpack(i + 1); // 进入下一层
}int main() {backpack(0); // 从第一个物品开始搜索cout << "最大总价值为:" << max_value << endl;return 0;
}
法二:
代码:
头文件:
#pragma once
#include<iostream>
#include<cmath>
#include<vector>
#include < algorithm>
using namespace std;源文件:
/*
* 回溯算法--01背包
*/
#include"01背包头文件.h"const int NUM = 50;
int c; //背包容纳的重量
int n; //物品数量
int cw; //当前重量
int cv; //当前价值
int bestv; //当前最优价值//描述每个物品的数据结构
struct Object {int w; //物品的重量int v; //物品的价值double d; //物品的单位价值重量比(d=v/w)
}Q[NUM]; //物品的数组bool cmp(Object a,Object b) {if (a.d>b.d){return true;}else{return false;}
}
//限界函数Bound()的实现
//形参i是回溯的深度
int Bound(int i) {int cleft = c - cw; // 背包剩余容纳的重量double b = cv; // 上界价值while (i < n && Q[i].w <= cleft) { // 尽量装满背包cleft -= Q[i].w;b += Q[i].v;i++;}if (i < n) { // 剩余空间不足以容纳物品 i 时,将物品 i 分配到背包中,直到背包装满b += 1.0 * Q[i].v / Q[i].w * cleft;}return b;
}//形参i是回溯的深度,从0开始
void backtrack(int i){if (i + 1 > n) {bestv = cv;return;}//进入左子树搜索if(cw+Q[i].w<=c) {cw = cw + Q[i].w;cv = cv + Q[i].v;backtrack(i + 1);cw = cw - Q[i].w;cv = cv - Q[i].v;}//进入右子树搜索if(Bound(i+1)>bestv){backtrack(i + 1);}
}int main() {cin >> c >> n; //输入背包容纳的重量和物品数量for (int i = 0; i < n; i++) {cin >> Q[i].w >> Q[i].v; //输入物品的重量和物品的价值Q[i].d = 1.0 * Q[i].v / Q[i].w; //物品的单位价值重量比(d=v/w)} //排序sort(Q, Q + n, cmp);backtrack(0);cout << "最大总价值为:" << bestv << endl; return 0;
}运行结果

代码改进
上面的代码已经实现了 01 背包问题的求解,但是还有一些需要改进的地方,以下是我的建议:
-
你在回溯函数 backtrack 中使用递归的方式进行搜索。虽然递归可以使得代码更加简洁,但是如果物品数量较大时,可能会导致栈溢出的问题。因此,建议采用迭代的方式进行搜索,使用一个栈来存储搜索状态。
-
在你的排序函数中,其实不必写成一个 bool 类型的函数,直接写成一个比较函数即可。例如:
bool cmp(Object a, Object b) {return a.d > b.d;
}
3.你在计算排序后的上界时,可能会出现除数为 0 的情况(当背包容量为 0 时)。因此,在计算物品的单位价值时,可以加上一个特判,例如:
if (Q[i].w == 0) {Q[i].d = 0;
} else {Q[i].d = 1.0 * Q[i].v / Q[i].w;
}
4.下面是修改过的代码:
/** 01 背包问题求解,回溯法实现* 输入格式:* 第一行包含背包容量 c 和物品数量 n,以空格分隔;* 接下来 n 行,每行包含一个物品的重量和价值,以空格分隔。* 输出格式:* 最大总价值*/#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;const int MAXN = 50;struct Object {int w, v; // 物品重量和价值double d; // 单位价值
};bool cmp(Object a, Object b) {return a.d > b.d;
}int main() {int c, n;cin >> c >> n;vector<Object> items(n);for (int i = 0; i < n; i++) {cin >> items[i].w >> items[i].v;if (items[i].w == 0) {items[i].d = 0;} else {items[i].d = 1.0 * items[i].v / items[i].w;}}sort(items.begin(), items.end(), cmp); // 按单位价值排序int bestv = 0; // 当前最优解vector<int> path(n); // 存储当前搜索路径int i = 0; // 当前搜索的物品编号int cw = 0; // 当前背包中物品的总重量int cv = 0; // 当前背包中物品的总价值while (true) {if (i >= n) { // 遍历完了所有物品,回溯if (bestv < cv) {bestv = cv;}if (path.empty()) {break; // 遍历完了所有状态,退出}i = path.back(); // 取出上一个搜索的物品path.pop_back();cw -= items[i].w;cv -= items[i].v;i++; // 进入右子树搜索} else if (cw + items[i].w <= c) { // 左子树搜索path.push_back(i);cw += items[i].w;cv += items[i].v;i++; // 进入左子树搜索} else { // 右子树搜索double bound = cv + (c - cw) * items[i].d; // 计算上界if (bound < bestv) {if (path.empty()) {break; // 遍历完了所有状态,退出}i = path.back(); // 取出上一个搜索的物品path.pop_back();cw -= items[i].w;cv -= items[i].v;i++; // 进入右子树搜索} else {i++; // 进入左子树搜索}}}cout << bestv << endl;return 0;
}
这段代码实现了 01 背包问题的回溯算法求解,并且采用了剪枝策略进行优化,基本思路如下:
首先,读入背包容量 c 和物品数量 n,以及每个物品的重量和价值。
将物品按单位价值从大到小排序,这里采用了 C++ STL 中的 sort 函数。
从第一个物品开始进行搜索,使用一个栈来保存搜索路径,路径上的每个节点包含当前已选中的物品编号、当前背包中已装载的物品总重量和总价值。
在搜索过程中,对于每个节点,分别考虑进入其左子树和右子树两种情况。左子树表示当前物品被选择放入背包,进入左子树后要将物品的重量和价值加入到当前背包中,并更新搜索路径;右子树表示当前物品不放入背包,进入右子树后只需要更新搜索路径即可。
在进入下一个节点之前,使用剪枝策略计算这个节点的上界。这里使用了线性松弛法(Linear Relaxation),即假设当前物品可以部分装入背包中,按单位价值从大到小的顺序装入物品直到背包装满,则此时背包中物品的总价值加上剩余空间能够容纳的物品的单位价值乘以其重量即为当前节点的上界。如果计算出来的上界小于当前已知的最优解,则可以剪枝,放弃进入左子树的搜索,直接进入右子树。因为进入左子树的搜索必然不会得到更优的解。
当遍历完所有节点后,输出当前的最优解即可。
总体而言,这段代码实现了一个简洁高效的 01 背包问题求解算法。
相关文章:

回溯算法--01背包问题
目录 回溯算法--01背包问题 [算法描述] [回溯法基本思想] 法一: 法二: 代码: 运行结果 代码改进 回溯算法--01背包问题 [算法描述] 0-1背包问题是子集选取问题。一般情况下,0-1背包问题是NP完全问题。0-1背包问题的解空…...
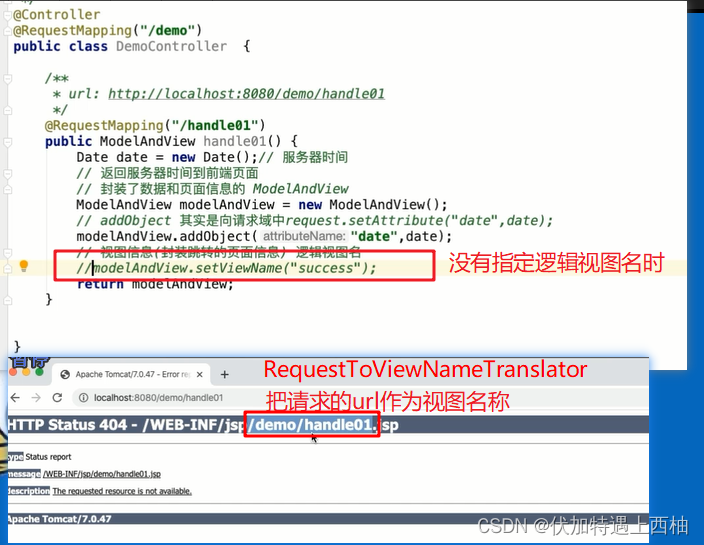
Spring MVC请求处理流程分析
Spring MVC请求处理流程分析一 Spring MVC 请求处理流程二 Spring MVC 请求处理流程源码分析2.1架构图解2.2 重要时机点分析2.3核心步骤分析2.3.1 getHandler⽅法剖析2.3.2 getHandlerAdapter⽅法剖析2.3.3 ha.handle⽅法剖析2.3.4 processDispatchResult⽅法剖析三 Spring MVC…...

Python高阶知识之属性管理
本文主要介绍Python高阶知识中的属性管理,这部分知识在常规Python编程中用的很少,但对于想深度了解Python甚至有志于自己编写实用框架的人,还是很有必要的,并且如果掌握了,对日常的代码学习等也会有一定好处。 本文结…...
【Linux】创建目录文件,并完成删除,拷贝,移动,比较等操作
操作前: 1.创建目录 mkdir命令 格式: mkdir 目录名 示例: 点击主文件夹查看 2.创建文件夹 touch命令 格式: touch 文件夹名 示例: 3.重命名文件 mv命令 格式 : mv 123.txt abc.txt 示…...

python http服务搭建教程
作为互联网时代的基础技术之一, HTTP是一个简单的 HTTP协议,它包含了请求、应答和超文本传输控制等机制。HTTP协议由 TCP/IP协议族定义,其中包括了三个基本的服务:发送、接收、存储。客户端和服务器之间传输信息时,数据…...

高速数字信号VS射频信号,到底哪个更难设计?
一博高速先生成员:黄刚熟悉高速先生的小伙伴们会知道,我们是以研究高速数字信号为主的团队,从不到1G到目前在研究的112G,高速先生就这样一直研究过来的,分享的案例也大多是以高速数字信号为主的案例。最近受到我们粉丝…...

相对路径读取json文件 labelme_shapes_to_label 标签
直接读取: import jsonwith open(file.json, r, encodingutf-8) as f:data json.load(f) 忽略错误读取: import jsonimport codecs with codecs.open(file.json, r, encodingutf-8, errorsignore) as f:data json.load(f) labelme_shapes_to_labe…...
IDEA工具避坑指南(十一):git导入SpringBoot后|不识别依赖 |大量爆红 | 无法启动
一、前言 使用在IDEA2019中,使用Git工具导入SpringBoot项目后,java类的依赖包大量爆红、不能启动SpringBoot,不能自动识别启动类。 提示:如果刚拉取的项目,只有.git和.idea文件,没有src或java目录ÿ…...
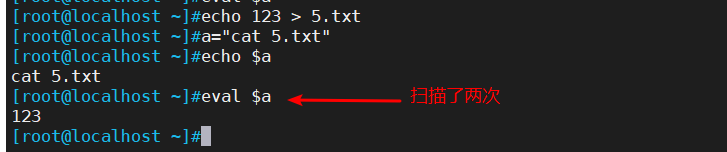
管道命令(sort、uniq、tr、cut、eval命令)
一、sort命令 1、作用 以行为单位对文件内容进行排序也可以根据不同的数据类型来排序 2、语法格式 sort [选项] 参数cat file | sort 选项3、常用选项 -f∶ 忽略大小写,会将小写字母都转换为大写字母来进行比较; -b∶ 忽略每行前面的空格;…...

Windows10系统忘记登录密码解决办法
Windows10系统忘记登录密码解决办法1. 前言1.1. 环境准备1.2. 官方PE安装系统2. 虚拟机配置2.1. 编辑虚拟机2.2. 进入固件2.3. 编辑启动项顺序2.4. 进入PE系统2.5. 恢复原系统3. 修改程序操作步骤3.1. 调用cmd程序3.2. 查看所有磁盘信息3.3. 进入原系统C盘3.4. 重命名程序3.5. …...
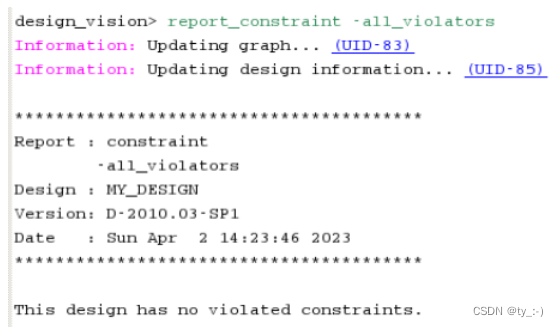
Design Complie实验,使用2007年Synopsy的Lab Guide
Design Complie实验,使用2007年Synopsy的Lab Guide 文章目录Design Complie实验,使用2007年Synopsy的Lab Guide1 DC实验1.1 Setup and Synthesis FlowTask 1 Update the setup fileTask 2 Invoke Design VisionTask 3 Read the Design into DC MemoryTas…...

问题 B: C语言10.2
题目描述: 输入a、b、c三个整数,按先大后小的顺序输出a、b和c。注意请使用指针变量的方式进行比较和输出。 输入 三个用空格隔开的整数a、b和c。 输出 按先大后小的顺序输出a、b和c,用空格隔开。 请注意行尾输出换行。 样例输入 9 0 1…...

多线程控制并发数目工具类Semaphore
文章目录前言Semaphore原理Semaphore源码解析内部继承AQS保证同步acquire获取许可release释放许可实战演示总结前言 在多线程编码过程中,我们会用到多线程来提升运行效率。比如我们的Executors创建线程池,程序尽可能的压榨CPU资源来提升我们程序吞吐量。…...

Redis篇之五大数据类型
1、五大数据类型 4.1、String(字符串) String是Redis最基本的类型,你可以理解成与Memcached一模一样的类型,一个key对应一个value String类型是二进制安全的。意味着Redis的string可以包含任何数据。比如jpg图片或者序列化的对象…...

Linux->文件系统磁盘文件管理
目录 1 磁盘结构 2 逻辑抽象管理磁盘 2.1 逻辑抽象 2.2 管理磁盘 2.3 补充知识 3 软硬连接 1 磁盘结构 本篇的学习需要建立在大家在脑海中有一副磁盘的结构才能进行下去,所以我会以图解的方式为大家简单讲解一下,注:博主对这一部分并不是…...
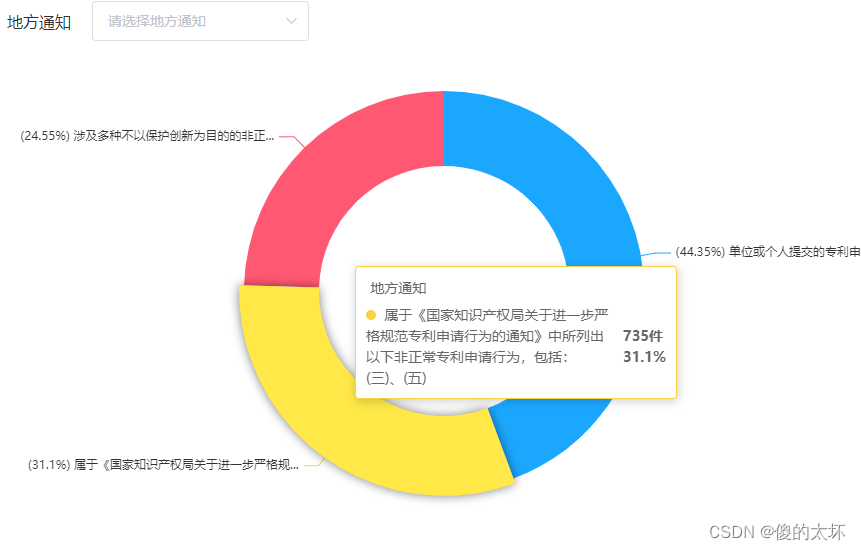
echarts tooltip文字太长换行
tooltip文字太长换行,设置了宽度也没有换行,加上一句: extraCssText: ‘max-width:300px; white-space:pre-wrap’, 没加之前是这样: 加上之后 extraCssText: ‘max-width:300px; white-space:pre-wrap’, tooltip: {trigger: &…...
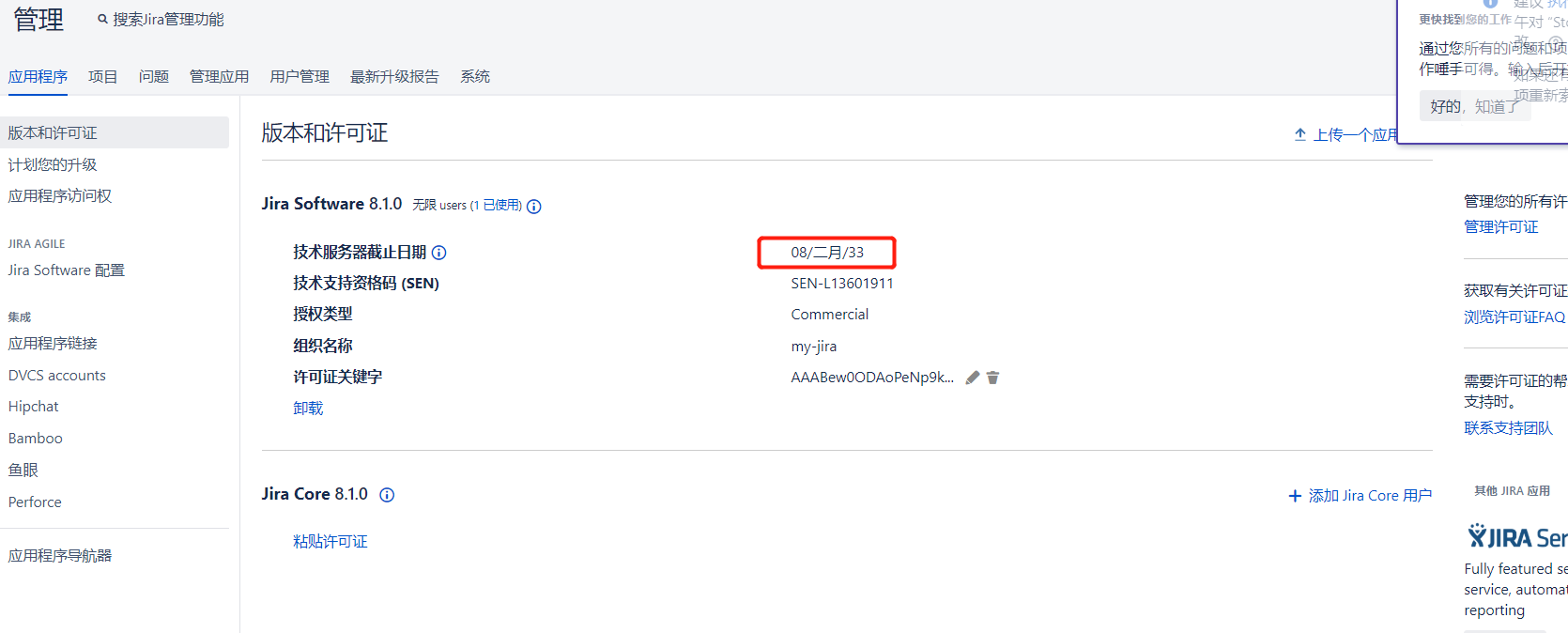
Docker 部署Jira8.1.0
Jira与Confluence一样,都需要用到独立的数据库,对于数据库的安装我们不做介绍,主要介绍如何用Docker部署Jira以及对Jira进行破解的操作。 1、数据库准备 关于数据库官方文档说明:https://confluence.atlassian.com/adminjiraserv…...
)
枚举、模拟法(蓝桥杯卡片、数的分解为例)
枚举和模拟算法是计算机领域常用的两种基本算法。枚举算法是一种通过列举所有可能的情况来解决问题的方法。模拟算法则是通过模拟真实场景来解决问题。 枚举、模拟法 枚举算法是指将问题分解为一系列离散的情况,通过枚举所有可能的情况,逐一检查每种情…...
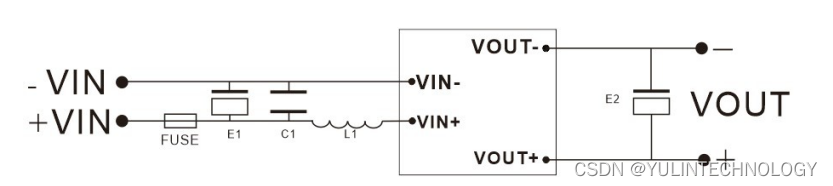
DC-DC升压变换器直流隔离高压输出稳压电源模块5v12v24v48v转50v110v150v220v250v300v350v500v
HRB 系列隔离宽电压输入高电压稳压输出 特点 效率高达 80%以上1*1英寸标准封装单电压输出稳压输出工作温度: -40℃~85℃阻燃封装,满足UL94-V0 要求温度特性好可直接焊在PCB 上应用 HRB 0.2~10W 系列模块电源是一种DC-DC升压变换器。该模块电源的输入电压分为&#…...

jQuery创建、添加、删除元素
一、创建元素 语法: $("<li></li>"); 动态的创建了一个 <li> 二、添加元素 1. 内部添加 1、element.append(内容) 把内容放入匹配元素内部最后面,类似原生 appendChild。 2、element.prepend(内容) 把内容放入匹…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...

jmeter聚合报告中参数详解
sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample(样本数) 表示测试中发送的请求数量,即测试执行了多少次请求。 单位,以个或者次数表示。 示例:…...
