枚举、模拟法(蓝桥杯卡片、数的分解为例)
枚举和模拟算法是计算机领域常用的两种基本算法。枚举算法是一种通过列举所有可能的情况来解决问题的方法。模拟算法则是通过模拟真实场景来解决问题。
枚举、模拟法
枚举算法是指将问题分解为一系列离散的情况,通过枚举所有可能的情况,逐一检查每种情况来解决问题。这种算法适合解决一些问题的最优解问题,但是当数据规模较大时会因为枚举的数量过多而导致运行时间增长。
模拟算法是指将一个问题的真实情况模拟出来,并对问题进行推演,以便得到问题的解决方案。
例如,蓝桥杯 卡片 - 蓝桥云课 (lanqiao.cn)
题目描述
用卡片拼数字,拼过的卡片不能再用,有 0 到 9 的卡片各 2021 张,共 20210 张,请问小蓝可以从 1拼到多少 ?
解题思路
比较容易的模拟,我们从1开始枚举,每次检查剩下的卡片能不能拼出这个数字就好。
把一个数在10进制下每个位置的数字求出来——先对10取模,个位上的数字就求出来了,再除以10,原本十位上的数字就变到了个位上,再对10取模...依次进行下去就求出来了。把当前拼的这个数每一位都拆出来,看看那个数字的卡片还够不够,不够的话就说明拼不了,这时候退出循环,所以最多拼到上一个数。
我的代码
#include <iostream>
using namespace std;
int main()
{// 请在此输入您的代码int a[10]={2021,2021,2021,2021,2021,2021,2021,2021,2021,2021};for(int i=0;i<20210;i++){int n = i;while(n) {int d = n % 10;if(a[d] == 0) {cout << i - 1 << endl;return 0;}a[d]--;n /= 10;} }return 0;
}例如,蓝桥杯 数的分解 - 蓝桥云课 (lanqiao.cn)
题目描述
把2019分解成3个各不相同的正整数之和,并且要求每个正整数都不包含数字2和4,一共有多少种不同的分解方法?
注意交换3个整数的顺序被视为同一种方法,例如1000+1001+18和1001+1000+18被视为同一种。
解题思路
我们定义这三个各不相同的正整数为i, j, k并且必须满足i<j<k。这样避免重复计算。
我们可以枚举i从1-2019 ,枚举j从1-2019,再枚举k从1-2019,这个题是填空题,这么干没问题,只是三个for循环的复杂度比较高,耗时长一些。
我们可以稍微优化一点点,比如可以考虑最内层的k ,当ij确定了之后,k的值自然就确定了,变成了2个for循环,复杂度就会降低一些,剩下我们只需要检查i,j,k 是否满足题目说的不含2和4即可。
怎么检查呢?
我们可以用字符串的函数to_string和find去做,详细见我的代码:
我的代码
#include <iostream>
using namespace std;
int main()
{// 请在此输入您的代码int sum=0,i,j,k;for(i=1;i<673;i++){for(j=i+1;j<1009;j++){k=2019-i-j;string a=to_string(i);string b=to_string(j);string c=to_string(k);if(a.find("2")==-1&&a.find("4")==-1&&b.find("2")==-1&&b.find("4")==-1&&c.find("2")==-1&&c.find("4")==-1)if(j<k)sum++;}}cout<<sum;return 0;
}
相关文章:
)
枚举、模拟法(蓝桥杯卡片、数的分解为例)
枚举和模拟算法是计算机领域常用的两种基本算法。枚举算法是一种通过列举所有可能的情况来解决问题的方法。模拟算法则是通过模拟真实场景来解决问题。 枚举、模拟法 枚举算法是指将问题分解为一系列离散的情况,通过枚举所有可能的情况,逐一检查每种情…...
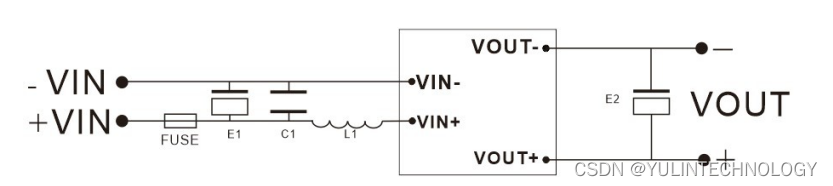
DC-DC升压变换器直流隔离高压输出稳压电源模块5v12v24v48v转50v110v150v220v250v300v350v500v
HRB 系列隔离宽电压输入高电压稳压输出 特点 效率高达 80%以上1*1英寸标准封装单电压输出稳压输出工作温度: -40℃~85℃阻燃封装,满足UL94-V0 要求温度特性好可直接焊在PCB 上应用 HRB 0.2~10W 系列模块电源是一种DC-DC升压变换器。该模块电源的输入电压分为&#…...

jQuery创建、添加、删除元素
一、创建元素 语法: $("<li></li>"); 动态的创建了一个 <li> 二、添加元素 1. 内部添加 1、element.append(内容) 把内容放入匹配元素内部最后面,类似原生 appendChild。 2、element.prepend(内容) 把内容放入匹…...

产品快讯丨神策数据 A/B 测试试验指标管理重磅升级
神策数据:为了更好地帮助企业管理试验指标,神策数据 A/B 测试完善了指标类型、配置方式、计算原理等,帮助分析师、运营同学等明确计算逻辑,并最大程度减少歧义以及与技术同学沟通的成本,以实现企业内部信息的有效统一。…...

游戏开发之Unity2021URP项目场景的构建
地面的修改和编辑:地面插件的使用 打开包管理器,在左边的包那里选择“Unity注册表”,在右边进行搜索“Polybrush”,之后选择右下角的安装 安装完之后要选择样本中的URP进行导入,因为我们的项目是URP渲染管线的&#x…...

数学分析:多元微积分1
卓里奇的数学分析的好处在于直接从多元函数来入手多元微积分,引出矩阵,十分自然。 紧集的概念,感觉直接用闭集去理解就行,(对于图形学来说)。 多元函数的极限,其实和单元函数并没有什么区别。 这…...

STC32G 三轮车负压电磁
文章目录前言整车效果控制思路循迹环岛处理障碍处理关键代码部分差比和以及当前速度计算角速度环速度环环岛处理障碍处理前言 年后就没怎么碰车了,到3月中旬换三轮了,可算有一点成效了,做个记录。 整车效果 三轮负压电磁慢速元素识别控制思…...

【编程小记】位运算 x -x 表示含义
位运算 x & -x 表示含义一、原码反码补码二、位运算 x & -x 表示含义三、最终结论一、原码反码补码 在计算机中,整数的数据的存储是按照补码的方式进行存储的 按照数据与0的大小,数据又被分为正数与负数 正数的原码反码补码相同。负数的原码&…...

信创PC利旧管理新模式,麒麟信安助力国家某部委实现高效云办公
2022年,国家某部委所有桌面终端均已完成信创PC替换,并将日常办公所需的办公Office套件、OA无纸化办公系统、即时通讯系统等全部迁移至信创PC,但在进行生产业务系统迁移时,该单位信创PC仍存在业务系统与不同芯片PC难适配、应用难兼…...
)
【玩转RT-Thread】RT-Thread内核宏定义详解(rtdef.h)
文章目录1.RT-Thread版本信息2.RT-Thrad基础数据类型定义3.RT-Thread基本数据类型的范围4.RT-Thread系统滴答时钟最大计数值5.RT-Thread IPC数据类型范围6.RT-Thread避免未使用变量警告7.编译器相关定义8.编译器相关定义9.RT-Thread错误码定义1.RT-Thread版本信息 /* RT-Threa…...

PDF转化器免费版有哪些?这几款办公达人们都在用
在现代办公中,文件的排版和格式是非常重要的,无论是发布通知或提交策划书、投档简历或是发表论文、宣传海报或是产品说明书等,我们经常使用PDF文件格式发送给他人。然而,很多人需要对PDF进行编辑修改,通常会先将其转换…...
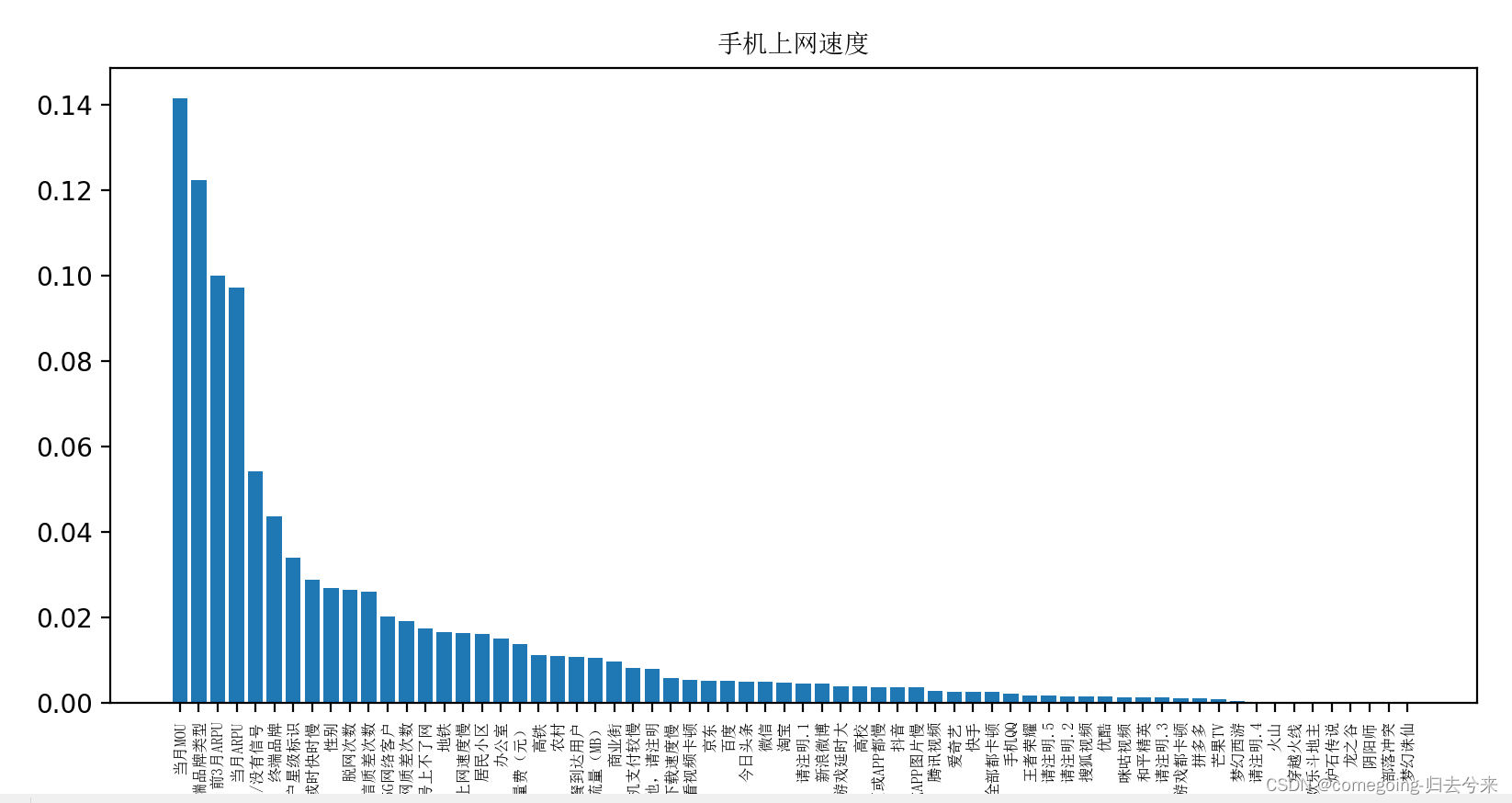
2022MathorCup赛题B
以下所有文字均基于作者的实际经验,并不具有完全的合理性,请谨慎参考 目录 一、问题分析 (一)问题一 (二)问题二 二、预处理 (一)训练集预处理 (二)测…...

适合销售使用的CRM系统特点
销售人员抱怨CRM系统太复杂,这是一个很重要的问题。毕竟,如果系统太难使用,会导致CRM实用率和效率下降,最终影响公司的运作。在这篇文章中,我们来探讨当销售抱怨crm客户系统太复杂了,企业该如何解决。 缺少…...

项目中获取resource下文件路径的方法
String filepathrequest.getServletContext().getRealPath("/")"files\\"; 获取的当前文件在实际运行的tomcat地址目录 String path ClassUtils.getDefaultClassLoader().getResource("").getPath()"tmp/files/"; 获取的是当前文件…...
Air32F103CBT6|CCT6|KEIL-uVsion5|本地编译|STClink|(6)、Air32F103编译下载
目录 一、环境搭建 准备工作 安装支持包 二、新建工程 添加外设库支持 测试代码 三、下载烧录 一、环境搭建 准备工作 安装MDK5,具体方法请百度,安装后需要激活才能编译大文件 下载安装AIR32F103的SDK:luatos-soc-air32f103: Air32f…...
)
结构(c的数据类型)
我们知道数组是相同类型元素的集合,那么结构就是不同类型的元素的集合,这些不同元素叫结构中的成员。是因为这些集合都有一定的联系才会归为一类的。 形式:我们知道,平时学习的int,double都叫类型,而结构是…...

前端常用的开工具库
常用的开发工具库 打包工具webpack webpack是现在最流行的打包工具之一,是javaScript的静态模块的打包器。会根据业务逻辑构建一个依赖的关系图,每一个依赖的单元都是一个模块,模块可以是js文件 可以图片资源或者css资源。在使用webpack的时…...

爬虫之数据库存储
在对于爬取数量数量较少时,我们可以将爬虫数据保存于CSV文件或者其他格式的文件中,既简单又方便,但是如果需要存储的数据量大,又要频繁访问这些数据时,就应该考虑将数据保存到数据库中了。目前主流的数据库有关系性数据…...
面试官:你可以用 for of 遍历 Object 吗?
本文以 用 for of遍历 Object 为引 来聊聊 迭代器模式。 什么是迭代器模式 迭代器模式提供一种方法顺序访问一个聚合对象中的各个元素,而又不暴露该对象的内部表示。 ——《设计模式:可复用面向对象软件的基础》 可以说迭代器模式就是为了遍历存在的。提…...

蓝桥杯基础12:BASIC-3试题 字母图形
资源限制 内存限制:256.0MB C/C时间限制:1.0s Java时间限制:3.0s Python时间限制:5.0s 问题描述 利用字母可以组成一些美丽的图形,下面给出了一个例子: ABCDEFG BABCDEF CBABCDE DCBABCD EDC…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...

Web后端基础(基础知识)
BS架构:Browser/Server,浏览器/服务器架构模式。客户端只需要浏览器,应用程序的逻辑和数据都存储在服务端。 优点:维护方便缺点:体验一般 CS架构:Client/Server,客户端/服务器架构模式。需要单独…...

苹果AI眼镜:从“工具”到“社交姿态”的范式革命——重新定义AI交互入口的未来机会
在2025年的AI硬件浪潮中,苹果AI眼镜(Apple Glasses)正在引发一场关于“人机交互形态”的深度思考。它并非简单地替代AirPods或Apple Watch,而是开辟了一个全新的、日常可接受的AI入口。其核心价值不在于功能的堆叠,而在于如何通过形态设计打破社交壁垒,成为用户“全天佩戴…...
