数学分析:多元微积分1

卓里奇的数学分析的好处在于直接从多元函数来入手多元微积分,引出矩阵,十分自然。

紧集的概念,感觉直接用闭集去理解就行,(对于图形学来说)。

多元函数的极限,其实和单元函数并没有什么区别。
这里引出了完备度量空间的概念,其实我一开始也没明白为什么基本点列会没有极限,后来查了才知道,对于一个开区间(a,b),如果它的基本点列最终的极限是b,那么因为b不在这个空间中,所以我们认为这个空间不是完备度量的空间。

这个还挺有意思的,对于极限趋于无穷的写法是,对于任何球的邻域,都可以找到一组基,使得这组基对应的像都不在这个球中。换句话说,再大的球,我们都可以找到一组基,使得基里的每个像都比这个球还要大,这就是无穷。

这里引出了道路的定义,就是一个区间I到R^n的连续映射。一般来说,就是闭区间[a,b],
根据f(t)=R^n的映射建立的道路。


一致连续的意思是,对于任何,都可以找到一个足够小的区间,在这个区间上的任何两点对应的像的距离都小于它。


这里面强调的紧集,可以理解成闭集(对于图形学)。

这是数学分析这本书里面的简写,但我感觉对于不习惯的人来说,理解起来很费劲。还是尽量用求和公式来表示吧。

我们把(7)用普通的求和公式来写:
具体子母上我做了调整。不过这里也可以看到爱因斯坦符号的好处,确实非常简洁。
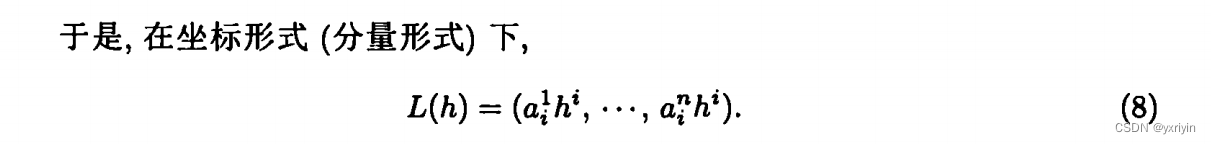
我们挑第一个分量验证下,
确实就是(8)

写成矩阵形式,就是(10),所以线性映射对应一个矩阵,而自变量对应一个向量,结果也是一个向量。

这是范数的定义,就是我们常规理解下的距离。
接下来的内容是非常重要的,我觉得有必要单独另起一篇来讲
相关文章:

数学分析:多元微积分1
卓里奇的数学分析的好处在于直接从多元函数来入手多元微积分,引出矩阵,十分自然。 紧集的概念,感觉直接用闭集去理解就行,(对于图形学来说)。 多元函数的极限,其实和单元函数并没有什么区别。 这…...

STC32G 三轮车负压电磁
文章目录前言整车效果控制思路循迹环岛处理障碍处理关键代码部分差比和以及当前速度计算角速度环速度环环岛处理障碍处理前言 年后就没怎么碰车了,到3月中旬换三轮了,可算有一点成效了,做个记录。 整车效果 三轮负压电磁慢速元素识别控制思…...

【编程小记】位运算 x -x 表示含义
位运算 x & -x 表示含义一、原码反码补码二、位运算 x & -x 表示含义三、最终结论一、原码反码补码 在计算机中,整数的数据的存储是按照补码的方式进行存储的 按照数据与0的大小,数据又被分为正数与负数 正数的原码反码补码相同。负数的原码&…...

信创PC利旧管理新模式,麒麟信安助力国家某部委实现高效云办公
2022年,国家某部委所有桌面终端均已完成信创PC替换,并将日常办公所需的办公Office套件、OA无纸化办公系统、即时通讯系统等全部迁移至信创PC,但在进行生产业务系统迁移时,该单位信创PC仍存在业务系统与不同芯片PC难适配、应用难兼…...
)
【玩转RT-Thread】RT-Thread内核宏定义详解(rtdef.h)
文章目录1.RT-Thread版本信息2.RT-Thrad基础数据类型定义3.RT-Thread基本数据类型的范围4.RT-Thread系统滴答时钟最大计数值5.RT-Thread IPC数据类型范围6.RT-Thread避免未使用变量警告7.编译器相关定义8.编译器相关定义9.RT-Thread错误码定义1.RT-Thread版本信息 /* RT-Threa…...

PDF转化器免费版有哪些?这几款办公达人们都在用
在现代办公中,文件的排版和格式是非常重要的,无论是发布通知或提交策划书、投档简历或是发表论文、宣传海报或是产品说明书等,我们经常使用PDF文件格式发送给他人。然而,很多人需要对PDF进行编辑修改,通常会先将其转换…...
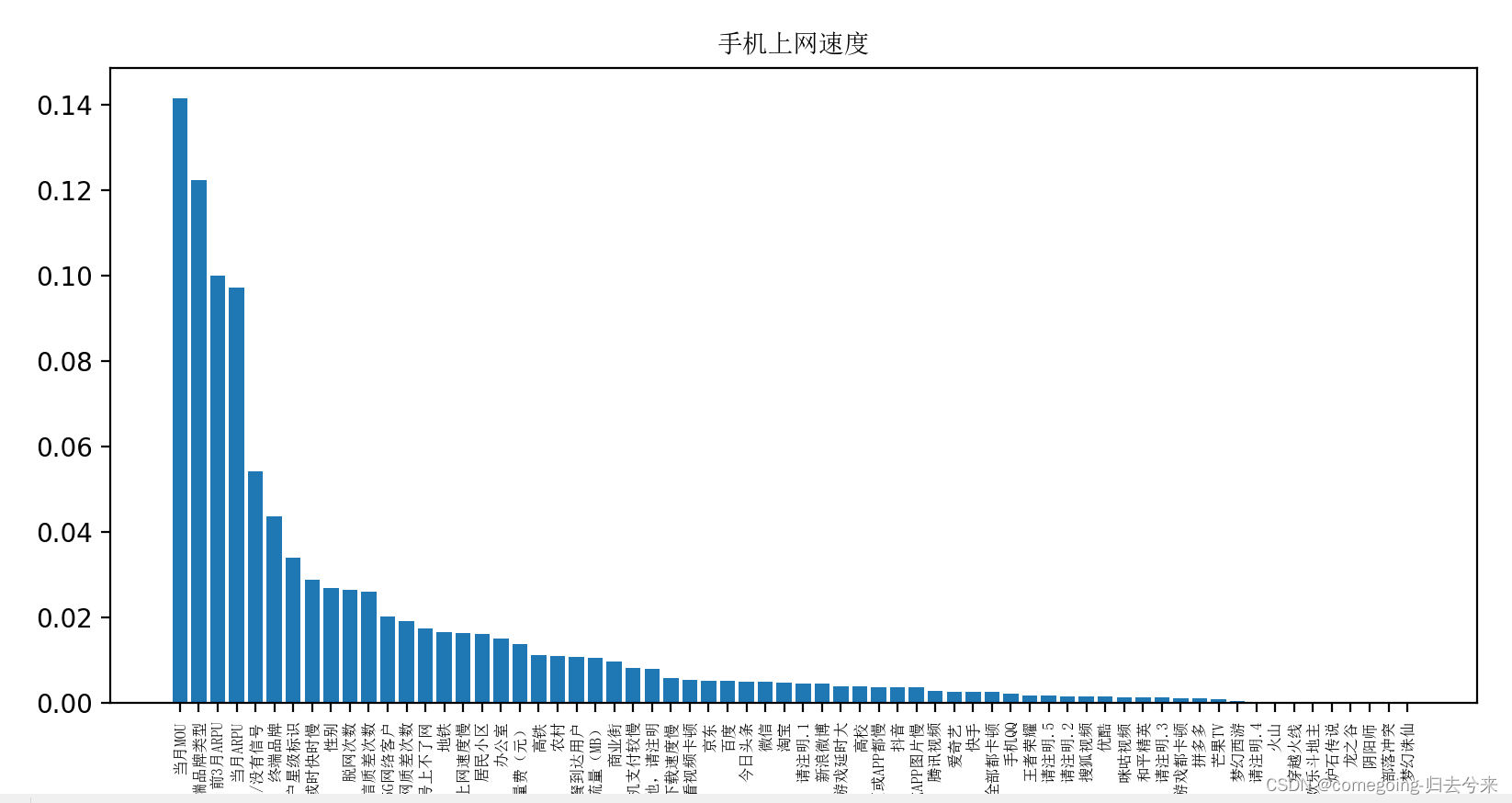
2022MathorCup赛题B
以下所有文字均基于作者的实际经验,并不具有完全的合理性,请谨慎参考 目录 一、问题分析 (一)问题一 (二)问题二 二、预处理 (一)训练集预处理 (二)测…...

适合销售使用的CRM系统特点
销售人员抱怨CRM系统太复杂,这是一个很重要的问题。毕竟,如果系统太难使用,会导致CRM实用率和效率下降,最终影响公司的运作。在这篇文章中,我们来探讨当销售抱怨crm客户系统太复杂了,企业该如何解决。 缺少…...

项目中获取resource下文件路径的方法
String filepathrequest.getServletContext().getRealPath("/")"files\\"; 获取的当前文件在实际运行的tomcat地址目录 String path ClassUtils.getDefaultClassLoader().getResource("").getPath()"tmp/files/"; 获取的是当前文件…...
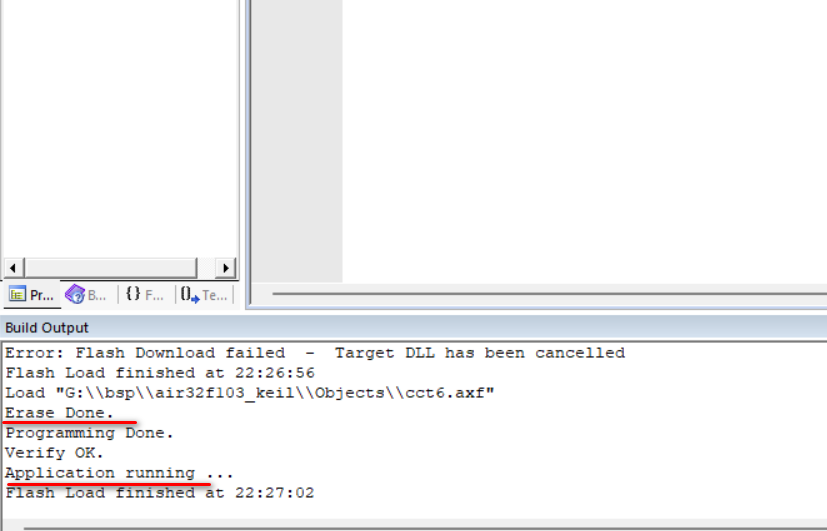
Air32F103CBT6|CCT6|KEIL-uVsion5|本地编译|STClink|(6)、Air32F103编译下载
目录 一、环境搭建 准备工作 安装支持包 二、新建工程 添加外设库支持 测试代码 三、下载烧录 一、环境搭建 准备工作 安装MDK5,具体方法请百度,安装后需要激活才能编译大文件 下载安装AIR32F103的SDK:luatos-soc-air32f103: Air32f…...
)
结构(c的数据类型)
我们知道数组是相同类型元素的集合,那么结构就是不同类型的元素的集合,这些不同元素叫结构中的成员。是因为这些集合都有一定的联系才会归为一类的。 形式:我们知道,平时学习的int,double都叫类型,而结构是…...

前端常用的开工具库
常用的开发工具库 打包工具webpack webpack是现在最流行的打包工具之一,是javaScript的静态模块的打包器。会根据业务逻辑构建一个依赖的关系图,每一个依赖的单元都是一个模块,模块可以是js文件 可以图片资源或者css资源。在使用webpack的时…...

爬虫之数据库存储
在对于爬取数量数量较少时,我们可以将爬虫数据保存于CSV文件或者其他格式的文件中,既简单又方便,但是如果需要存储的数据量大,又要频繁访问这些数据时,就应该考虑将数据保存到数据库中了。目前主流的数据库有关系性数据…...
面试官:你可以用 for of 遍历 Object 吗?
本文以 用 for of遍历 Object 为引 来聊聊 迭代器模式。 什么是迭代器模式 迭代器模式提供一种方法顺序访问一个聚合对象中的各个元素,而又不暴露该对象的内部表示。 ——《设计模式:可复用面向对象软件的基础》 可以说迭代器模式就是为了遍历存在的。提…...

蓝桥杯基础12:BASIC-3试题 字母图形
资源限制 内存限制:256.0MB C/C时间限制:1.0s Java时间限制:3.0s Python时间限制:5.0s 问题描述 利用字母可以组成一些美丽的图形,下面给出了一个例子: ABCDEFG BABCDEF CBABCDE DCBABCD EDC…...
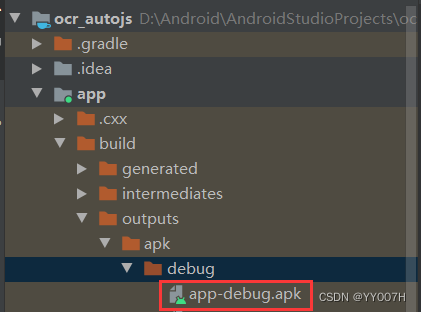
基于PaddleOCR开发懒人精灵文字识别插件
目的 懒人精灵是 Android 平台上的一款自动化工具,它通过编写 lua 脚本,结合系统的「 无障碍服务 」对 App 进行自动化操作。在文字识别方面它提供的有一款OCR识别插件,但是其中有识别速度慢,插件大的缺点,所以这里将讲…...

PyTorch 深度学习实战 | DIEN 模拟兴趣演化的序列网络
01、实例:DIEN 模拟兴趣演化的序列网络深度兴趣演化网络(Deep Interest Evolution Network,DIEN)是阿里巴巴团队在2018年推出的另一力作,比DIN 多了一个Evolution,即演化的概念。在DIEN 模型结构上比DIN 复杂许多,但大家丝毫不用担心,我们将DIEN 拆解开来详细地说明…...

pyspark null类型 在 json.dumps(null) 之后,会变为字符串‘null‘
在将 hive 数仓数据写入 MySQL 时候,有时我们需将数据转为 json 字符串,然后再存入 MySQL。但 hive 数仓中的 null 类型遇到 json 函数之后会变为 ‘null’ 字符串,这时我们只需在使用 json 函数之前对值进行判断即可,当值为 null…...
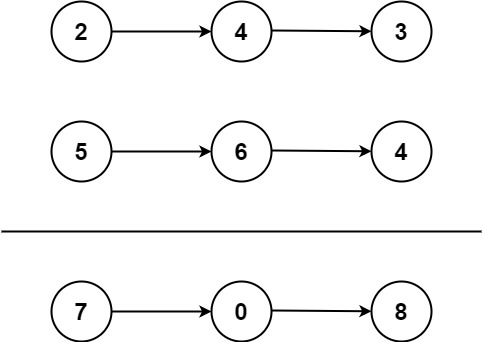
LeetCode - 两数相加
题目信息 源地址:两数相加 给你两个 非空 的链表,表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的,并且每个节点只能存储 一位 数字。 请你将两个数相加,并以相同形式返回一个表示和的链表。 你可以假设除了数字…...
Office 2021专业版安装包及激活教程
[软件名称]: Office 2021 [软件大小]: 4.33GB [安装环境]: Win11/Win 10 [软件安装包下载]:https://pan.quark.cn/s/169ed49988b2 “Microsoft Office 2021是Microsoft推出的办公软件。2021年10月5日,Office 2021 for Mac发布,其中包含许多新功能 Micro…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...

给网站添加live2d看板娘
给网站添加live2d看板娘 参考文献: stevenjoezhang/live2d-widget: 把萌萌哒的看板娘抱回家 (ノ≧∇≦)ノ | Live2D widget for web platformEikanya/Live2d-model: Live2d model collectionzenghongtu/live2d-model-assets 前言 网站环境如下,文章也主…...

CppCon 2015 学习:Time Programming Fundamentals
Civil Time 公历时间 特点: 共 6 个字段: Year(年)Month(月)Day(日)Hour(小时)Minute(分钟)Second(秒) 表示…...
