算法训练营 - 广度优先BFS
目录
从层序遍历开始
N 叉树的层序遍历
经典BFS最短路模板
经典C++ queue
数组模拟队列
打印路径
示例1.bfs查找所有连接方块
C++queue版
数组模拟队列
示例2.从多个位置同时开始BFS
示例3.抽象最短路类(作图关键)
示例4.跨过障碍的最短路
从层序遍历开始
广度优先搜索(Breadth First Search,BFS),又称为宽度优先搜索,是最常见的图搜索方法之一。广度优先搜索是从某个顶点(源点)出发,一次性访问所有未被访问的邻接点,再依次从这些访问过邻接点出发,…,似水中涟漪,似声音传播,一层层地传播开来。
广度优先遍历是按照广度优先搜索的方式对图进行遍历。
广度优先搜索模型
Bfs()
{
1. 建立起始步骤,队列初始化
2. 遍历队列中的每一种可能,whlie(队列不为空)
{
通过队头元素带出下一步的所有可能,并且依次入队
{
判断当前情况是否达成目标:按照目标要求处理逻辑
}
继续遍历队列中的剩余情况
}
}
(看不懂没有关系,直接看题就完事儿了)
N 叉树的层序遍历
力扣
/*
// Definition for a Node.
class Node {
public:int val;vector<Node*> children;Node() {}Node(int _val) {val = _val;}Node(int _val, vector<Node*> _children) {val = _val;children = _children;}
};
*/class Solution {
public:vector<vector<int>> levelOrder(Node* root) {vector<int> v;vector<vector<int>> vec;queue<Node*> q;if(!root) return vec;q.push(root);//将开始bfs位置入队while(!q.empty()){int n=q.size();//需要遍历这一层的元素个数for(int i=0;i<n;i++)//记录该层元素并将其所连接的点入队{Node* temp=q.front();q.pop();if(!temp) continue;v.push_back(temp->val);//将这个点所连接的点入队vector<Node*> son=temp->children;for(int j=0;j<son.size();j++)q.push(son[j]); }vec.push_back(v);v.clear();}return vec;}
};经典BFS最短路模板
经典C++ queue
#include <iostream>
#include <cstring>
#include <queue>
using namespace std;const int N = 110;
typedef pair<int, int> PII;
int n, m;
int g[N][N], d[N][N];int bfs()
{queue< pair<int, int> > q;q.push({0, 0});memset(d, -1, sizeof(d));d[0][0] = 0;int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};while (q.size())//队列不为空{PII t = q.front();//取队头元素q.pop();//出队for (int i = 0; i < 4; i++){int x = t.first + dx[i], y = t.second + dy[i];if (x >= 0 && x < n && y >= 0 && y < m && g[x][y] == 0 && d[x][y] == -1){d[x][y] = d[t.first][t.second] + 1;//当前点到起点的距离q.push({x, y});//将新坐标入队}}}return d[n - 1][m -1];
}int main()
{cin >> n >> m;for (int i = 0; i < n; i++)for (int j = 0; j < m; j++)cin >> g[i][j];cout << bfs() << endl;return 0;
}数组模拟队列
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 110;
typedef pair<int, int> PII;
int n, m;
int g[N][N];//存放地图
int d[N][N];//存 每一个点到起点的距离
PII q[N * N];//手写队列
int bfs()
{int hh = 0, tt = 0;q[0] = {0, 0};memset(d, - 1, sizeof d);//距离初始化为- 1表示没有走过d[0][0] = 0;//表示起点走过了int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};//x 方向的向量和 y 方向的向量组成的上、右、下、左while(hh <= tt)//队列不空{PII t = q[hh ++ ];//取队头元素for(int i = 0; i < 4; i ++ )//枚举4个方向{int x = t.first + dx[i], y = t.second + dy[i];//x表示沿着此方向走会走到哪个点if(x >= 0 && x < n && y >= 0 && y < m && g[x][y] == 0 && d[x][y] == -1)//在边界内 并且是空地可以走 且之前没有走过{d[x][y] = d[t.first][t.second] + 1;//到起点的距离q[ ++ tt ] = {x, y};//新坐标入队}}}return d[n - 1][m - 1]; //输出右下角点距起点的距离即可
}
int main()
{cin >> n >> m;for(int i = 0; i < n; i ++ )for(int j = 0; j < m; j ++ )cin >> g[i][j];cout << bfs() << endl;return 0;
}打印路径
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 110;
typedef pair<int, int> PII;
PII q[N*N],Prev[N][N];
int g[N][N], d[N][N];
int n, m;
int bfs()
{int hh = 0, tt = 0;q[0] = {0, 0};memset(d, -1, sizeof d);int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};d[0][0] = 0;while(hh <= tt){PII t = q[hh ++ ];for(int i = 0; i < 4; i ++ ){int x = dx[i] + t.first, y = t.second + dy[i];if(x >= 0 && x < n && y >= 0 && y < m && g[x][y] == 0 && d[x][y] == -1){d[x][y] = d[t.first][t.second] + 1;Prev[x][y] = t;q[++ tt] = {x, y};}}}int x = n - 1, y = m - 1;while(x || y)//有一个不d等于0{cout << x << ' ' << y << endl;PII t = Prev[x][y];x = t.first, y = t.second;}return d[n - 1][m - 1];
}
int main()
{cin >> n >> m;for(int i = 0; i < n; i ++ )for(int j = 0; j < m;j ++)cin >> g[i][j];cout << bfs() << endl;return 0;
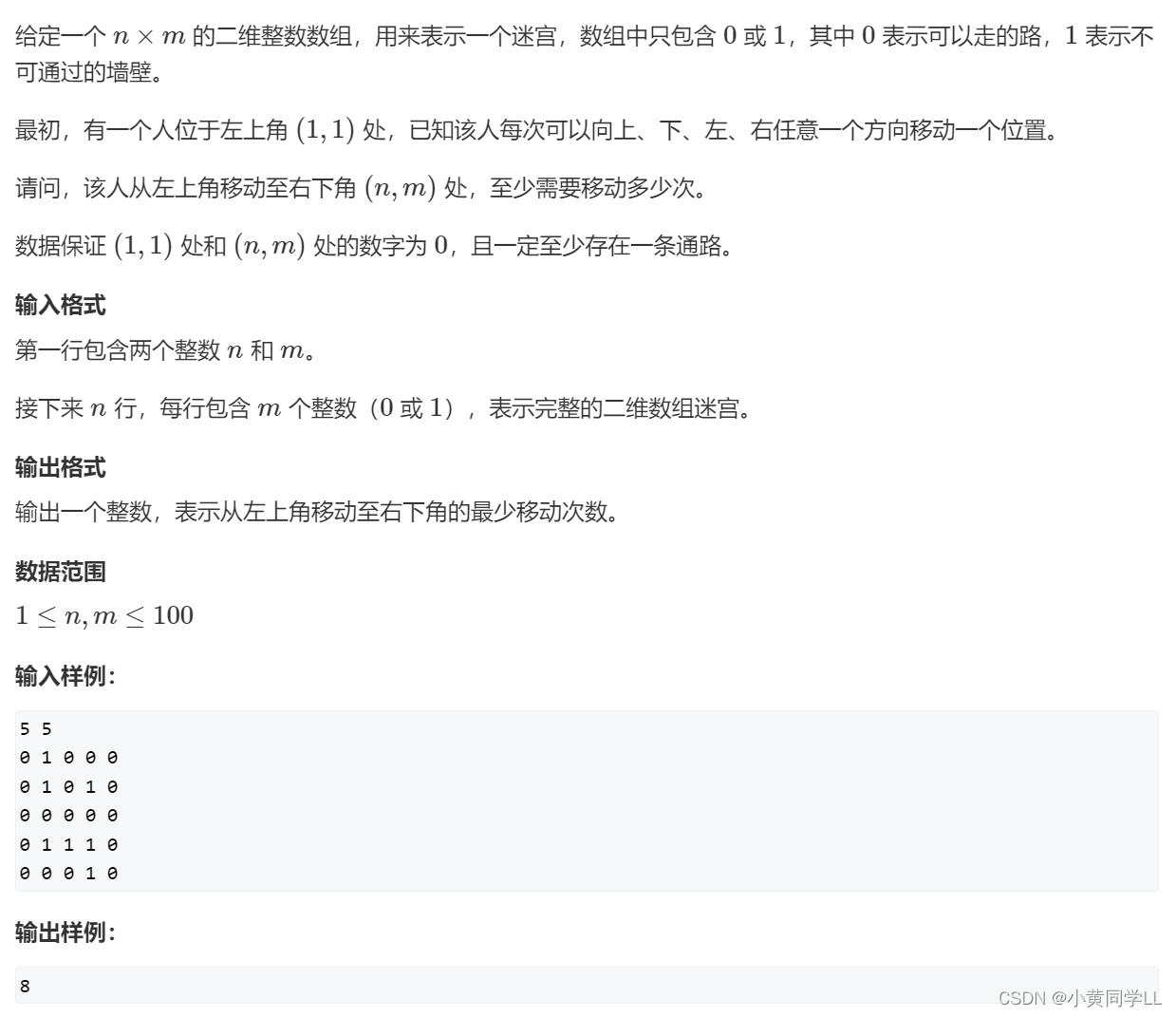
}输入
5 5
0 1 0 0 0
0 1 0 1 0
0 0 0 0 0
0 1 1 1 0
0 0 0 1 0输出
4 4
3 4
2 4
2 3
2 2
2 1
2 0
1 0
8示例1.bfs查找所有连接方块
力扣
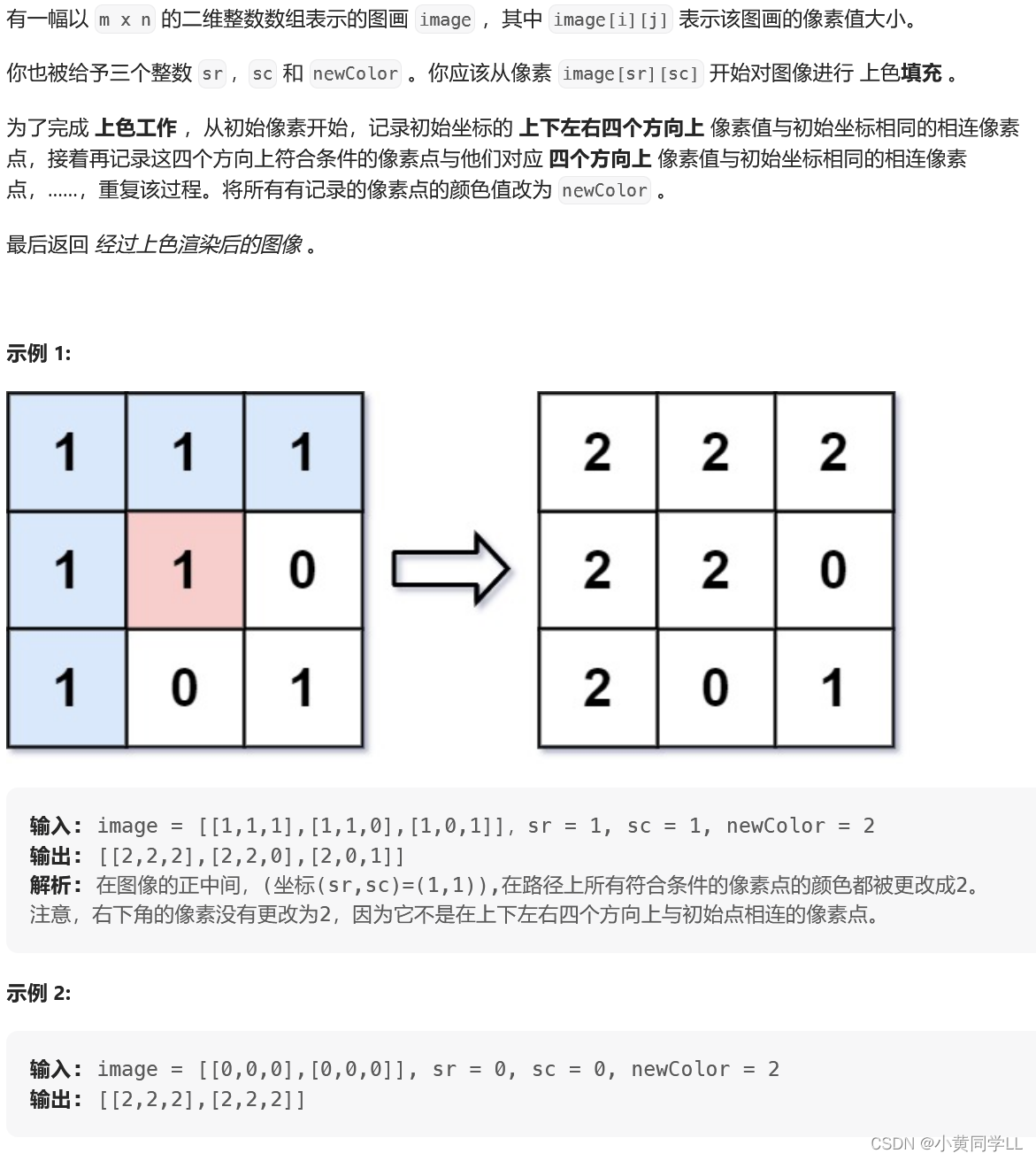
思路:
非常简单,就是把图块的四个方向都搜索一遍,对于每个相邻的同色图块修改成新色即可
C++queue版
class Solution {
public:const int dx[4]={1,-1,0,0},dy[4]={0,0,1,-1};vector<vector<int>> floodFill(vector<vector<int>>& image, int sr, int sc, int color) {int old=image[sr][sc];if(old==color) return image;int n=image.size(),m=image[0].size();queue<pair<int,int>> q;q.push({sr,sc});image[sr][sc]=color;while(!q.empty()){pair<int,int> t=q.front();q.pop();for(int i=0;i<4;i++){int x=t.first+dx[i],y=t.second+dy[i];if(x>=0&&x<n&&y>=0&&y<m&&image[x][y]==old){q.push({x,y});image[x][y]=color;}}}return image;}
};数组模拟队列
class Solution {
public:const int dx[4] = {1, 0, 0, -1},dy[4] = {0, 1, -1, 0};vector<vector<int>> floodFill(vector<vector<int>>& image, int sr, int sc, int color) {int old = image[sr][sc];if (old == color) return image;int n = image.size(), m = image[0].size();int hh=0,tt=0;pair<int,int> q[n*m];q[0]={sr,sc};image[sr][sc] = color;while (hh<=tt) {pair<int,int> t=q[hh++];for (int i = 0; i < 4; i++) {int x = t.first+dx[i], y = t.second+dy[i];if (x >= 0 && x < n && y >= 0 && y < m && image[x][y] == old) {q[++tt]={x,y};image[x][y] = color;}}}return image;}
};示例2.从多个位置同时开始BFS
力扣

本题可以先找到所有的腐烂橘子,入队,用第一批带出新一批腐烂的橘子
每以匹橘子都会在一分钟之内腐烂,所以此题可以转化为求BFS执行的大循环的次数
这里的step的更新需要有一个标记,只有新的腐烂的橘子加入,step才能自加
最后BFS执行完之后,说明所有可以被腐烂的都完成了,再去遍历grid,如何还有
值为1的,说明没有办法完全腐烂,返回-1,如果没有,则返回step
class Solution {
public:int dx[4]={1,-1,0,0},dy[4]={0,0,1,-1};int orangesRotting(vector<vector<int>>& grid) {int n=grid.size(),m=grid[0].size();queue<pair<int,int>> q;int cnt=0;int step=0;for(int i=0;i<n;i++)for(int j=0;j<m;j++)if(grid[i][j]==2) q.push({i,j});else if(grid[i][j]==1) cnt++;while(!q.empty()){int tot=q.size();bool flag=false;while(tot--)//多个位置同时开始{pair<int,int> t=q.front();q.pop();for(int i=0;i<4;i++){int x=t.first+dx[i],y=t.second+dy[i];if(x>=0&&x<n&&y>=0&&y<m&&grid[x][y]==1){q.push({x,y});grid[x][y]=2;cnt--;flag=true;}}}if(flag) ++step;}return cnt?-1:step; }
};示例3.抽象最短路类(作图关键)
力扣

思路:
- 通过BFS, 首先用beginWord带出转换一个字母之后所有可能的结果
- 每一步都要把队列中上一步添加的所有单词转换一遍,最短的转换肯定在这些单词当中, 所有这些词的转换只能算一次转换,因为都是上一步转换出来的,这里对于每个单词的每个位置都可以用26个字母进行转换,所以一个单词一次转换的可能有:单词的长度 * 26
- 把转换成功的新词入队,进行下一步的转换
- 最后整个转换的长度就和BFS执行的次数相同
class Solution {
public:int ladderLength(string beginWord, string endWord, vector<string>& wordList) {//hash表的查询效率最高,将单词存入哈希表unordered_set<string> wordDict(wordList.begin(), wordList.end());//标记单词是否已经访问过,访问过的不再访问unordered_set<string> visited;visited.insert(beginWord);//初始化队列queue<string> q;q.push(beginWord);int res = 1;while (!q.empty()) {int nextSize = q.size();while (nextSize--){string curWord = q.front();q.pop();if (curWord == endWord)return res ;//尝试转换当前单词的每一个位置for (int i = 0; i < curWord.size(); i++) {string newWord = curWord;//每一个位置用26个字母分别替换for (char ch = 'a'; ch <= 'z'; ch++) {newWord[i] = ch;//在字典里且没有用过if (wordDict.count(newWord) && !visited.count(newWord)){visited.insert(newWord);//标记用过q.push(newWord);} }}}res++;}//转换不成功,返回0return 0;}
};示例4.跨过障碍的最短路
力扣

障碍指不可到达的路径,这种障碍一般用数组或者hash表存储,用if判断此路不通;
思路:
深度优先不适合解此题,递归深度太大,会导致栈溢出
本题的密码为4位密码,每位密码可以通过拨动一次进行改变,注意这里的数的回环以及拨动的方向
拨动方向:向前,向后
回环:如果当前是9,0时,向前,向后拨动需要变成最小最大,而不是简单的自加自减
class Solution {
public:int openLock(vector<string>& deadends, string target) {// 哈希表的查找更快unordered_set<string> deadendsSet(deadends.begin(), deadends.end());//如果"0000"在死亡字符串中,则永远到达不了if (deadendsSet.find("0000") != deadendsSet.end())return -1;//初始化队列queue<string> que;que.push("0000");//加标记,已经搜索过的字符串不需要再次搜索unordered_set<string> book;book.insert("0000");int step = 0;while (!que.empty()) {int n = que.size();//从上一步转换之后的字符串都需要进行验证和转换//并且只算做一次转换,类似于层序遍历,转换的步数和层相同//同一层的元素都是经过一步转换得到的while(n--) {string curStr = que.front();que.pop();if (curStr == target) return step;//四位密码锁,每个位置每次都可以转一次for (int j = 0; j < 4; j++) {string newStr1 = curStr, newStr2 = curStr;//当前位置可以向前或者向后拨一位newStr1[j] = newStr1[j] == '9' ? '0' : newStr1[j] + 1;newStr2[j] = newStr2[j] == '0' ? '9' : newStr2[j] - 1;//如果不会死锁且没有尝试过,则入队if (deadendsSet.find(newStr1) == deadendsSet.end()&& book.find(newStr1) == book.end()) {que.push(newStr1);book.insert(newStr1);}if (deadendsSet.find(newStr2) == deadendsSet.end()&& book.find(newStr2) == book.end()) {que.push(newStr2);book.insert(newStr2);}}}step++;}return -1;}
};
相关文章:

算法训练营 - 广度优先BFS
目录 从层序遍历开始 N 叉树的层序遍历 经典BFS最短路模板 经典C queue 数组模拟队列 打印路径 示例1.bfs查找所有连接方块 Cqueue版 数组模拟队列 示例2.从多个位置同时开始BFS 示例3.抽象最短路类(作图关键) 示例4.跨过障碍的最短路 从层序遍历…...
)
判断两个字符串是否匹配(1个通配符代表一个字符)
目录 判断两个字符串是否匹配(1个通配符代表一个字符) 程序设计 程序分析...

用css画一个csdn程序猿
效果如下: 头部 我们先来拆解一下,程序猿的结构 两只耳朵和头是圆形组成的,耳朵内的红色部分也是圆形 先画头部,利用圆角实现头部形状 借助工具来快速实现圆角效果 https://9elements.github.io/fancy-border-radius/ <div…...

Java多线程编程—wait/notify机制
文章目录1. 不使用wait/notify机制通信的缺点2. 什么是wait/notify机制3. wait/notify机制原理4. wait/notify方法的基本用法5. 线程状态的切换6. interrupt()遇到方法wait()7. notify/notifyAll方法8. wait(long)介绍9. 生产者/消费者模式10. 管道机制11. 利用wait/notify实现…...

Three.js教程:旋转动画、requestAnimationFrame周期性渲染
推荐:将NSDT场景编辑器加入你3D工具链其他工具系列:NSDT简石数字孪生基于WebGL技术开发在线游戏、商品展示、室内漫游往往都会涉及到动画,初步了解three.js可以做什么,深入讲解three.js动画之前,本节课先制作一个简单的…...

租车自驾app开发有什么作用?租车便利出行APP开发
在线租车APP有哪些优势,租车APP开发的基本功能,租车自驾app开发有什么作用?租车便利出行APP开发,租车服务平台小程序有哪些功能,租车软件开发需要多少钱,租车app都有哪些,租车平台定制开发,租车…...

linux shell 文件分割
split 按照 10m 大小进行分割 split -b 10m large_file.bin new_file_prefix...
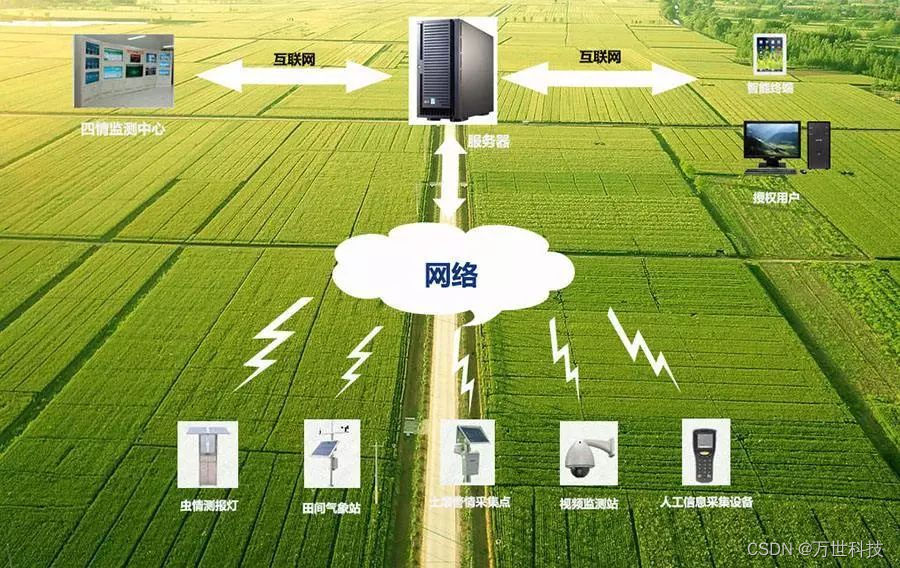
智慧农业系统开发功能有哪些?
农业从古至今都是备受关注的话题,新时代背景下农业发展已经融合了互联网,数字化技术等新型发展方式,形成了农业物联网管控系统,让农业生产更加科技化、智能化、高效化,对农业可持续发展有巨大的推动作用。所以…...

【C语言】 指针的进阶 看这一篇就够了
目录 1.字符指针 2.数组指针 3.指针数组 4.数组传参和指针传参 5.函数指针 6.函数指针数组 7.指向函数指针数组的指针 8.回调函数 9.qsort排序和冒泡排序 1.字符指针 让我们一起来回顾一下指针的概念! 1.指针就是一个变量,用来存放地址,地址…...

redis set list
Listlist: 插入命令:lpush / rpush 查看list列表所有数据(-1 表示最后一个):lrange key 0 -1 查看列表长度(key 不存在则长度返回0 ): llen key list长度 获取下表 为 0 的元素 修改下标为0的元素,改为haha 移除列表的第一个元素 或最后一…...

如何解决DNS劫持
随着互联网的不断发展,DNS(域名系统)成为了构建网络基础的重要组成部分。而DNS遭到劫持,成为一种常见的安全问题。那么DNS遭到劫持是什么意思呢?如何解决DNS劫持问题呢?下面就让小编来为您一一解答。 DNS遭到劫持是什么意思? DNS遭到劫持指的是黑客通…...

【LeetCode】剑指 Offer(28)
目录 题目:剑指 Offer 54. 二叉搜索树的第k大节点 - 力扣(Leetcode) 题目的接口: 解题思路: 代码: 过啦!!! 题目:剑指 Offer 55 - I. 二叉树的深度 - 力…...

「ML 实践篇」模型训练
在训练不同机器学习算法模型时,遇到的各类训练算法大多对用户都是一个黑匣子,而理解它们实际怎么工作,对用户是很有帮助的; 快速定位到合适的模型与正确的训练算法,找到一套适当的超参数等;更高效的执行错…...
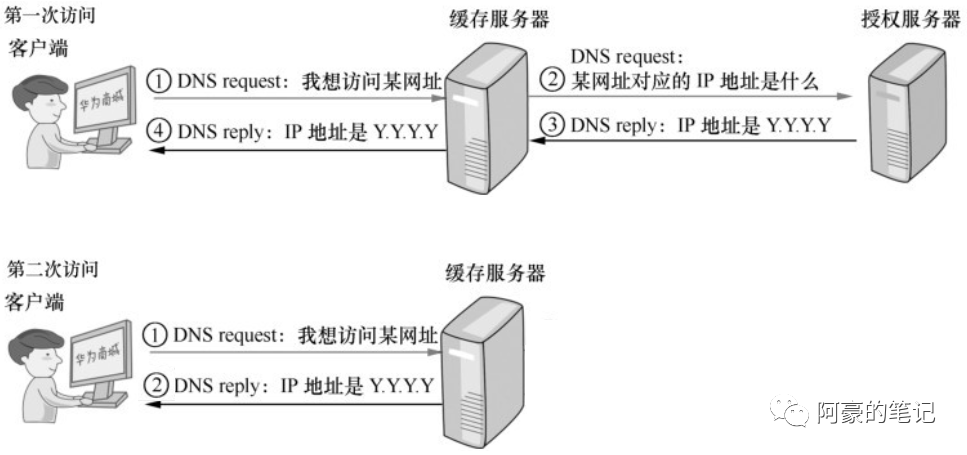
域名解析协议-DNS
DNS(Domain Name System)是互联网上非常重要的一项服务,我们每天上网都要依靠大量的DNS服务。在Internet上,用户更容易记住的是域名,但是网络中的计算机的互相访问是通过 IP 地址实现的。DNS 最常用的功能是给用户提供…...

分享:包括 AI 绘画在内的超齐全免费可用的API 大全
AI 绘画已经火出圈了,你还不知道哪里可以用嘛?我给大家整理了超级齐全的免费可用 API,包括 AI 绘画在内,有需要的小伙伴赶紧收藏了。 AI 绘画/AI 作画 类 AI 绘画:通过AI 生成图片,包括图生文、文生图等。…...

虹科新闻 | 虹科与Overland-Tandberg正式建立合作伙伴关系
虹科Overland-Tandberg 近日,虹科与美国Overland-Tandberg公司达成战略合作,虹科正式成为Overland-Tandberg公司在中国区域的认证授权代理商。未来,虹科将携手Overland-Tandberg,共同致力于提供企业数据管理和保护解决方案。 虹科…...
架构设计三原则
作为程序员,很多人都希望成为一名架构师,但并非简单地通过编程技能就能够达成这一目标。事实上,优秀的程序员和架构师之间存在一个明显的鸿沟——不确定性。 编程的本质是确定性的,也就是说,对于同一段代码,…...
Android 性能优化——ANR监控与解决
作者:Drummor 1 哪来的ANR ANR(Application Not responding):如果 Android 应用的界面线程处于阻塞状态的时间过长,会触发“应用无响应”(ANR) 错误。如果应用位于前台,系统会向用户显示一个对话框。ANR 对话框会为用户提供强制退出应用的选项…...
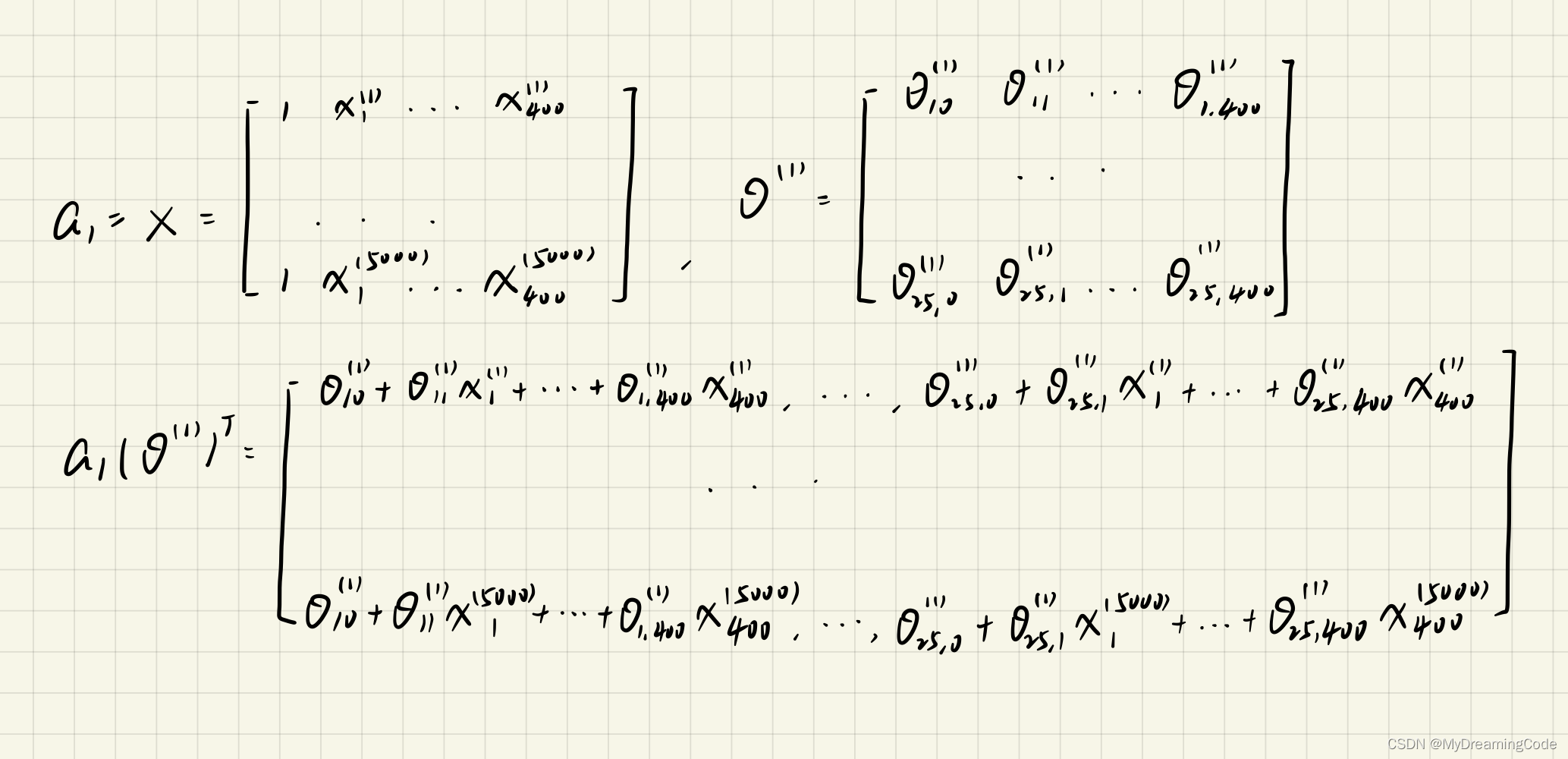
Machine Learning-Ex3(吴恩达课后习题)Multi-class Classification and Neural Networks
目录 1. Multi-class Classification 1.1 Dataset 1.2 Visualizing the data 1.3 Vectorizing Logistic Regression 1.3.1 Vectorizing the cost function(no regularization) 1.3.2 Vectorizing the gradient(no regularization&#…...

【Java】SpringBoot事务回滚规则
SpringBoot事务回滚规则SpringBoot事务回滚规则SpringBoot事务回滚规则 在SpringBoot中,如果一个方法被声明为Transactional,则会开启一个事务。如果这个方法中的任何一个步骤失败了(比如抛出了异常),则该事务将会回滚…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

ubuntu系统文件误删(/lib/x86_64-linux-gnu/libc.so.6)修复方案 [成功解决]
报错信息:libc.so.6: cannot open shared object file: No such file or directory: #ls, ln, sudo...命令都不能用 error while loading shared libraries: libc.so.6: cannot open shared object file: No such file or directory重启后报错信息&…...

Matlab实现任意伪彩色图像可视化显示
Matlab实现任意伪彩色图像可视化显示 1、灰度原始图像2、RGB彩色原始图像 在科研研究中,如何展示好看的实验结果图像非常重要!!! 1、灰度原始图像 灰度图像每个像素点只有一个数值,代表该点的亮度(或…...

Java后端检查空条件查询
通过抛出运行异常:throw new RuntimeException("请输入查询条件!");BranchWarehouseServiceImpl.java // 查询试剂交易(入库/出库)记录Overridepublic List<BranchWarehouseTransactions> queryForReagent(Branch…...

