Machine Learning-Ex3(吴恩达课后习题)Multi-class Classification and Neural Networks
目录
1. Multi-class Classification
1.1 Dataset
1.2 Visualizing the data
1.3 Vectorizing Logistic Regression
1.3.1 Vectorizing the cost function(no regularization)
1.3.2 Vectorizing the gradient(no regularization)
1.3.3 Vectorizing regularized logistic regression
1.4 One-vs-all Classification
1.4.1 One-vs-all Prediction
2. Neural Networks
2.1 Model representation
2.2 Feedforward Propagation and Prediction
1. Multi-class Classification
1.1 Dataset
内容:5000个20*20像素的手写字体图像与它对应的数字,其中数字0的值用10表示。
main.py
# scipy.io模块提供了很多函数来处理Matlab的数组
from scipy.io import loadmat # loadmat方法可以导入Matlab格式数据data = loadmat('ex3data1.mat')
print(data)
print(data['X'].shape, data['y'].shape) # (5000, 400) (5000, 1){'__header__': b'MATLAB 5.0 MAT-file, Platform: GLNXA64, Created on: Sun Oct 16 13:09:09 2011', '__version__': '1.0', '__globals__': [], 'X': array([[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
...,
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.],
[0., 0., 0., ..., 0., 0., 0.]]), 'y': array([[10],
[10],
[10],
...,
[ 9],
[ 9],
[ 9]], dtype=uint8)}
(5000, 400) (5000, 1)
1.2 Visualizing the data
内容:随机展示100个数据。
main.py
# scipy.io模块提供了很多函数来处理Matlab的数组
from scipy.io import loadmat # loadmat方法可以导入Matlab格式数据
import numpy as npdata = loadmat('ex3data1.mat')
# np.random.choice(a,size=None,replace=True,p=None)
# 1.从a(必须是一维)中随机取数字,组成大小为size的数组;replace-True表示可以取相同数字;p-a中每个元素被取的概率,默认为每个元素概率相同
# np.arange(start,stop,step)用于生成数组-开始位置,停止位置,步长,即在给定间隔内返回均匀间隔的值
# print(np.arange(data['X'].shape[0])) # [ 0 1 2 ... 4997 4998 4999]
sample_index = np.random.choice(np.arange(data['X'].shape[0]), 100) # 从0-4999中随机抽取100个数作为下标
sample_images = data['X'][sample_index, :] # 抽取下标为sample_index的这些X的数据行
print(sample_images)
[[0. 0. 0. ... 0. 0. 0.]
[0. 0. 0. ... 0. 0. 0.]
[0. 0. 0. ... 0. 0. 0.]
...
[0. 0. 0. ... 0. 0. 0.]
[0. 0. 0. ... 0. 0. 0.]
[0. 0. 0. ... 0. 0. 0.]]
plot_training_set.py
import numpy as np
import matplotlib.pyplot as plt
import matplotlib # 使用matplotlib.cm色表def plotTrainingSet(data):sample_index = np.random.choice(np.arange(data['X'].shape[0]), 100) # 从0-4999中随机抽取100个数作为下标sample_images = data['X'][sample_index, :] # 抽取下标为sample_index的这些X的数据行 (100*400)# subplots(nrows,ncols,sharex,sharey)-子图的行列数,sharex/sharey为True时所有子图共享x或y轴,为False时子图的x,y轴均为独立fig, axs = plt.subplots(nrows=10, ncols=10, sharex=True, sharey=True, figsize=(10, 10))# 1.使用axs[i][j]选中第i+1行j+1列的子图框# 2.matplotlib.pyplot.matshow(A,cmap),A-"矩阵"(一个矩阵元素对应一个图像像素),cmap-一种颜色映射方式# 3.matplotlib.cm为色表,binary为灰度图像标准色表,matshow为可绘制矩阵的函数# 4.xticks(ticks,labels),ticks-x轴刻度位置的列表,若传入空列表则不显示x轴,labels-放在指定刻度位置的标签文本for i in range(10):for j in range(10):axs[i][j].matshow(sample_images[i * 10 + j].reshape(20, 20).T, cmap=matplotlib.cm.binary)plt.xticks(np.array([]))plt.yticks(np.array([]))plt.show()
main.py
# scipy.io模块提供了很多函数来处理Matlab的数组
from scipy.io import loadmat # loadmat方法可以导入Matlab格式数据
from plot_training_set import * # 绘制训练集数据data = loadmat('ex3data1.mat')
plotTrainingSet(data)

1.3 Vectorizing Logistic Regression
内容:因为有10个数字类别,所以我们要做10个不同的逻辑回归分类器。将逻辑回归向量化会使训练效率更加高效。
1.3.1 Vectorizing the cost function(no regularization)
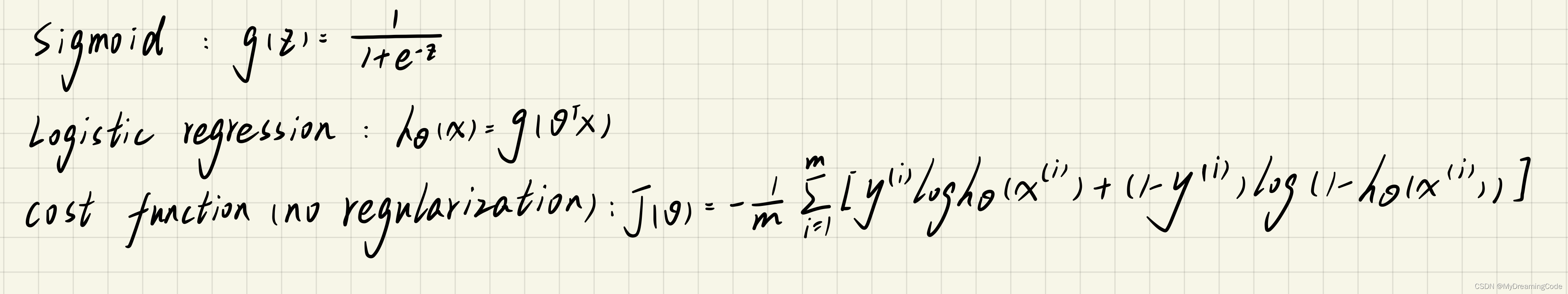
sigmoid.py
import numpy as np
def Sigmoid(z):return 1 / (1 + np.exp(-z))
cost_function.py(with regularization)
import numpy as np
from sigmoid import *def costFunction(theta, X, y, learningRate):theta = np.matrix(theta)X = np.matrix(X)y = np.matrix(y)m = len(X)first = np.multiply(y, np.log(Sigmoid(X * theta.T)))second = np.multiply(1 - y, np.log(1 - Sigmoid(X * theta.T)))reg = (learningRate / (2 * m)) * np.sum(np.power(theta[:, 1:theta.shape[1]], 2)) # theta0项不用正则化return np.sum(first + second) * (-1) / m + reg
1.3.2 Vectorizing the gradient(no regularization)
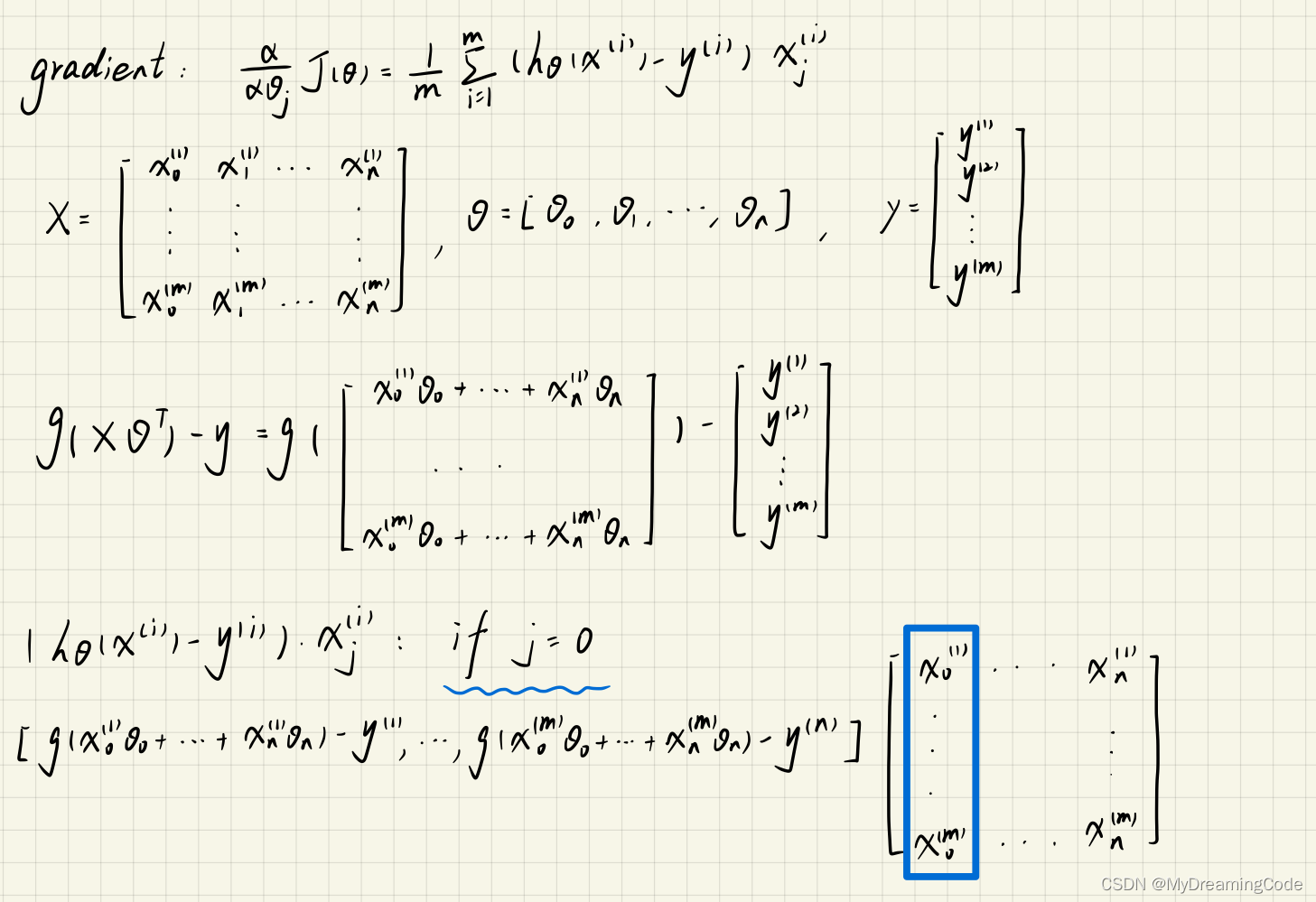
gradient.py
import numpy as np
from sigmoid import *def computeGradient(theta, X, y):X = np.matrix(X)y = np.matrix(y)theta = np.matrix(theta)m = len(X)grad = ((Sigmoid(X * theta.T) - y).T * X) / mreturn grad
1.3.3 Vectorizing regularized logistic regression

gradient.py
import numpy as np
from sigmoid import *def computeGradient(theta, X, y, learningRate):X = np.matrix(X)y = np.matrix(y)theta = np.matrix(theta)m = len(X)grad = ((((Sigmoid(X * theta.T) - y).T * X)).T + learningRate * theta.T) / mgrad[0][0] = (Sigmoid(X * theta.T) - y).T * X[:, 0] / mreturn grad
1.4 One-vs-all Classification
内容:构建分类器,由于逻辑回归只能在两个类别之间进行分类,所以我们需要多类分类的策略。对于每一个分类器我们只需要判断它的类别是'i'或者不是'i'即可。
one_vs_all.py
from scipy.optimize import minimize # 提供最优化算法函数
import numpy as np
from cost_function import * # 代价函数
from gradient import * # 梯度def one_vs_all(X, y, num_labels, learningRate):rows = X.shape[0]cols = X.shape[1]all_theta = np.zeros((num_labels, cols + 1)) # 对于num_labels(10分类)的全部theta定义X = np.insert(X, 0, values=np.ones(rows), axis=1) # 放入X0项,为1 (axis=1:按列放置)# 进行逻辑分类(做10个分类器)for i in range(1, num_labels + 1):theta = np.zeros(cols + 1)y_i = np.array([1 if label == i else 0 for label in y]).reshape(rows, 1)y_i = np.reshape(y_i, (rows, 1))# 1.fun:目标函数costFuntion# 2.x0:初始的猜测# 3.args=():优化的附加参数# 4.计算梯度的方法# method:要使用的方法名称,这里使用的TNC(截断牛顿算法)fmin = minimize(fun=costFunction, x0=theta, args=(X, y_i, learningRate), method='TNC', jac=computeGradient)all_theta[i - 1:] = fmin.x # fmin.x是theta的值return all_theta
main.py
# scipy.io模块提供了很多函数来处理Matlab的数组
from scipy.io import loadmat # loadmat方法可以导入Matlab格式数据
import numpy as np
from one_vs_all import *data = loadmat('ex3data1.mat')
X = data['X']
y = data['y']
theta = np.zeros(X.shape[1])
all_theta = one_vs_all(X, y, 10, 1)
print(all_theta)
[[-2.38358610e+00 0.00000000e+00 0.00000000e+00 ... 1.30435711e-03
-7.45365860e-10 0.00000000e+00]
[-3.18324551e+00 0.00000000e+00 0.00000000e+00 ... 4.45577193e-03
-5.07998907e-04 0.00000000e+00]
[-4.79716788e+00 0.00000000e+00 0.00000000e+00 ... -2.87443285e-05
-2.47862001e-07 0.00000000e+00]
...
[-7.98546406e+00 0.00000000e+00 0.00000000e+00 ... -8.95211947e-05
7.22094621e-06 0.00000000e+00]
[-4.57261766e+00 0.00000000e+00 0.00000000e+00 ... -1.33564925e-03
9.98868166e-05 0.00000000e+00]
[-5.40500039e+00 0.00000000e+00 0.00000000e+00 ... -1.16648642e-04
7.88651180e-06 0.00000000e+00]]
1.4.1 One-vs-all Prediction
内容:使用之前训练好的分类器来预测标签(概率最大的那一类即为标签,精确度可达94%)。
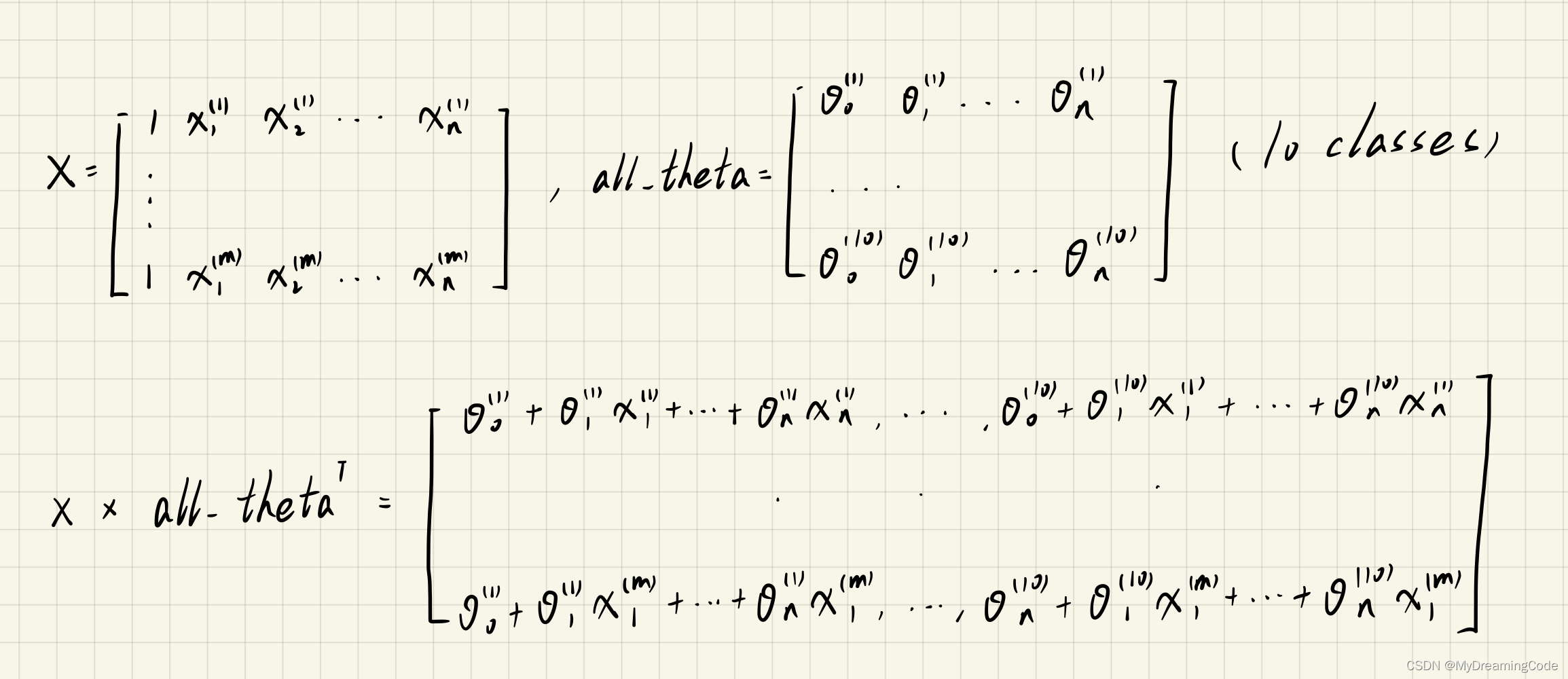
predict_all.py
import numpy as np
from sigmoid import *def predictAll(X, all_theta):rows = X.shape[0]X = np.insert(X, 0, values=np.ones(rows), axis=1)X = np.matrix(X)all_theta = np.matrix(all_theta)h_theta = Sigmoid(X * all_theta.T)# np.argmax(arr,axis)返回数组arr中最大值的索引值h_theta_max = np.argmax(h_theta, axis=1)return h_theta_max + 1
main.py
# scipy.io模块提供了很多函数来处理Matlab的数组
from scipy.io import loadmat # loadmat方法可以导入Matlab格式数据
import numpy as np
from sklearn.metrics import classification_report # 常用的输出模型评估报告方法
from one_vs_all import *
from predict_all import * # 预测h_theta值data = loadmat('ex3data1.mat')
X = data['X']
y = data['y']
theta = np.zeros(X.shape[1])
all_theta = one_vs_all(X, y, 10, 1)
y_pred = predictAll(X, all_theta)
# classification_report(y_true,y_pred)y_true:真实值,y_pred:预测值
print(classification_report(y, np.array(y_pred)))
# precision recall f1-score support
# 精确率 召回率 调和平均数 支持度(指原始的真实数据中属于该类的个数)
precision recall f1-score support
1 0.95 0.99 0.97 500
2 0.95 0.92 0.93 500
3 0.95 0.91 0.93 500
4 0.95 0.95 0.95 500
5 0.92 0.92 0.92 500
6 0.97 0.98 0.97 500
7 0.95 0.95 0.95 500
8 0.93 0.92 0.92 500
9 0.92 0.92 0.92 500
10 0.97 0.99 0.98 500accuracy 0.94 5000
macro avg 0.94 0.94 0.94 5000
weighted avg 0.94 0.94 0.94 5000
2. Neural Networks
内容:神经网络可以处理比较复杂的非线性模型,这里给出了已经训练好的权重,我们使用前向传播即可。
2.1 Model representation
内容:
theta1:25*401 theta2:10*26
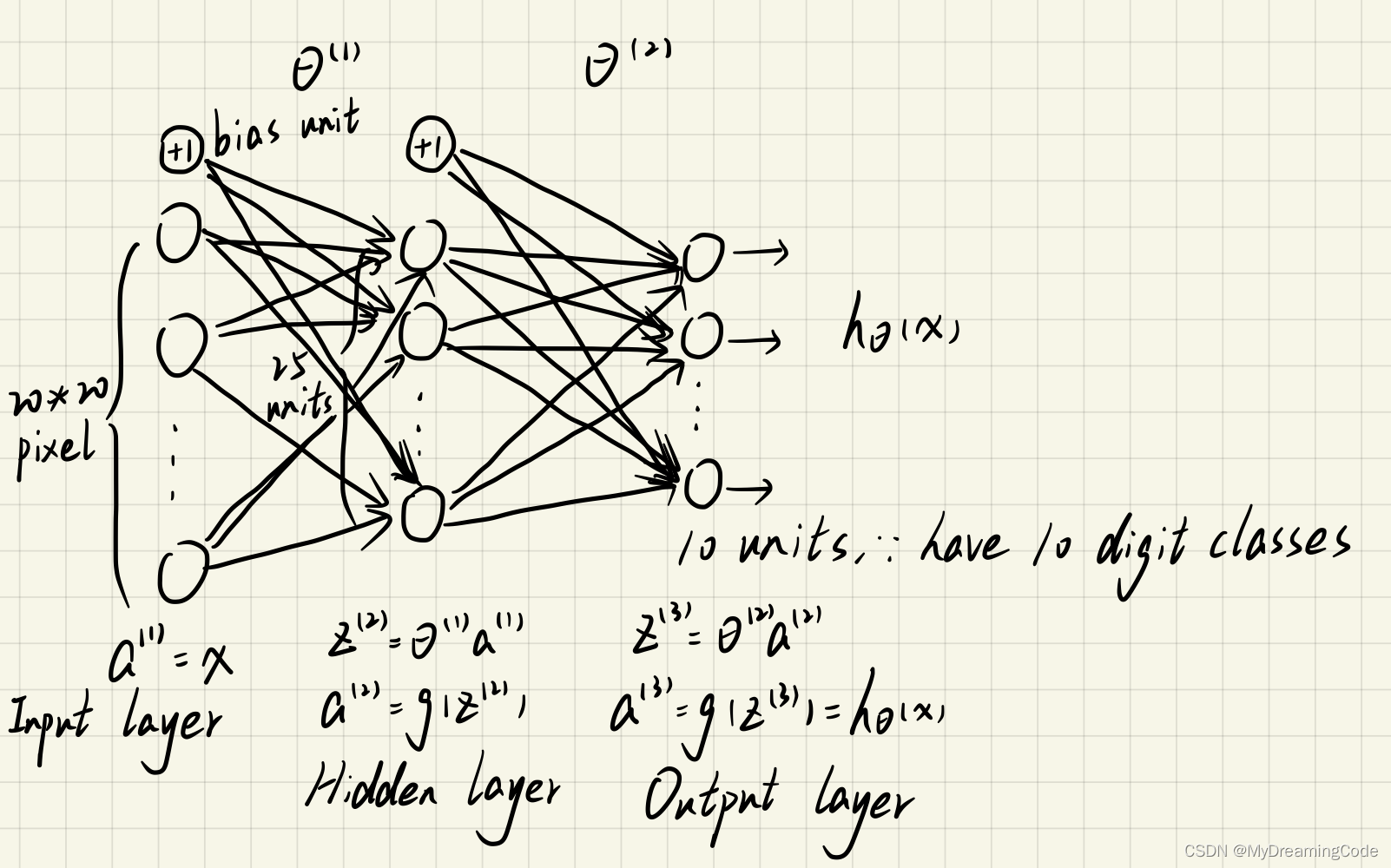
main.py
from scipy.io import loadmat
import numpy as npdata = loadmat('../ex3data1.mat')
X = np.matrix(data['X'])
X = np.insert(X, 0, values=np.ones(X.shape[0]), axis=1) # axis=1即按列插入
y = np.matrix(data['y'])
weights = loadmat('ex3weights.mat')
theta1, theta2 = np.matrix(weights['Theta1']), np.matrix(weights['Theta2'])
print(theta1.shape, theta2.shape, X.shape, y.shape)
(25, 401) (10, 26) (5000, 401) (5000, 1)
2.2 Feedforward Propagation and Prediction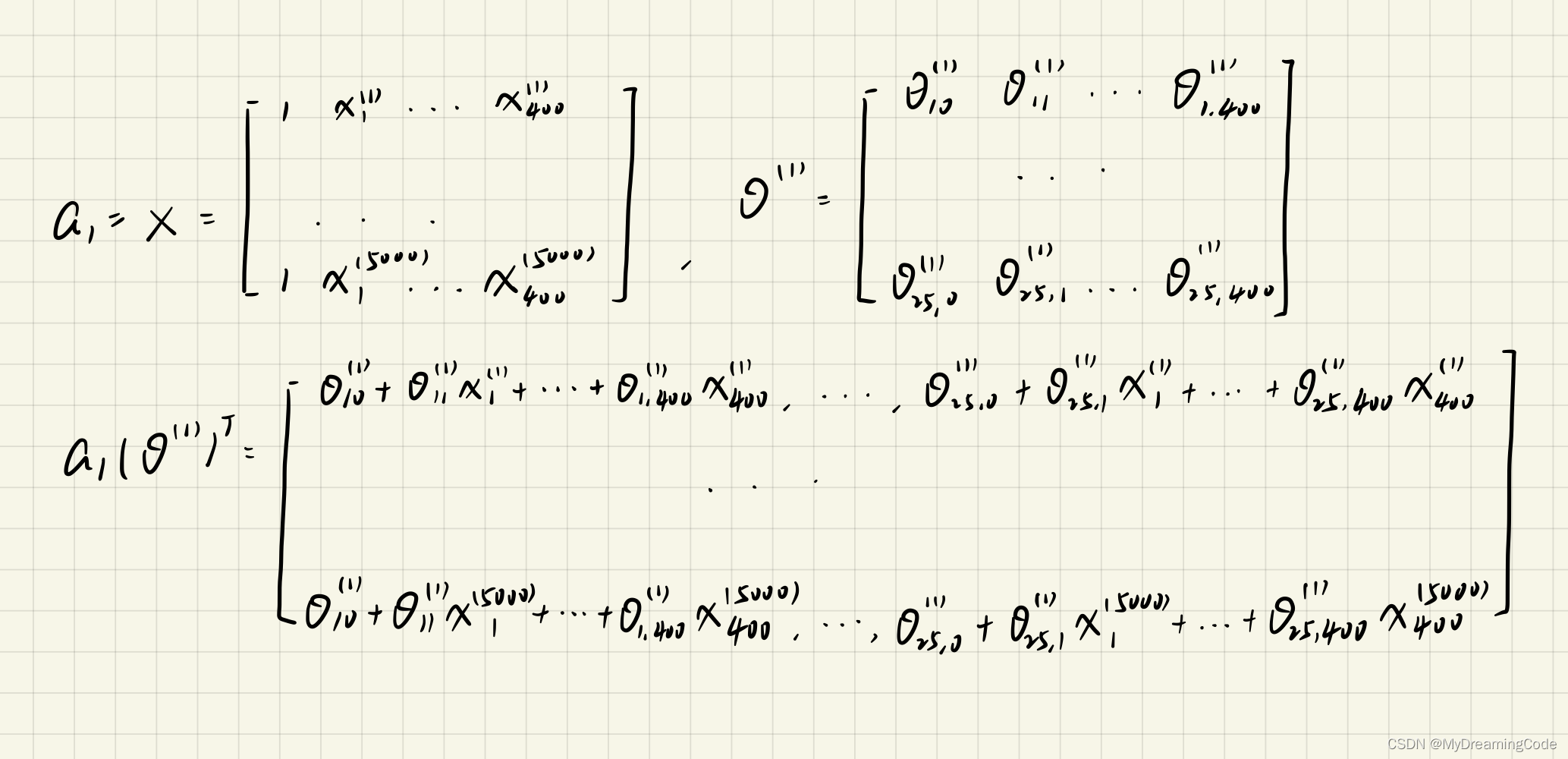
sigmoid.py
import numpy as npdef Sigmoid(z):return 1 / (1 + np.exp(-z))
main.py(输出a3,即h_theta的值)
from scipy.io import loadmat
import numpy as np
from sigmoid import * # 激活函数data = loadmat('../ex3data1.mat')
X = np.matrix(data['X'])
X = np.insert(X, 0, values=np.ones(X.shape[0]), axis=1) # axis=1即按列插入
y = np.matrix(data['y'])
weights = loadmat('ex3weights.mat')
theta1, theta2 = np.matrix(weights['Theta1']), np.matrix(weights['Theta2'])# 神经网络-前向反馈
a1 = X
z2 = a1 * theta1.T
# print(z2.shape) # (5000, 25)
a2 = Sigmoid(z2)
a2 = np.insert(a2, 0, values=np.ones(a2.shape[0]), axis=1) # 加偏置项,值为1
z3 = a2 * theta2.T
# print(z3.shape) # (5000,10)
a3 = Sigmoid(z3) # h_theta
print(a3)
[[1.12661530e-04 1.74127856e-03 2.52696959e-03 ... 4.01468105e-04
6.48072305e-03 9.95734012e-01]
[4.79026796e-04 2.41495958e-03 3.44755685e-03 ... 2.39107046e-03
1.97025086e-03 9.95696931e-01]
[8.85702310e-05 3.24266731e-03 2.55419797e-02 ... 6.22892325e-02
5.49803551e-03 9.28008397e-01]
...
[5.17641791e-02 3.81715020e-03 2.96297510e-02 ... 2.15667361e-03
6.49826950e-01 2.42384687e-05]
[8.30631310e-04 6.22003774e-04 3.14518512e-04 ... 1.19366192e-02
9.71410499e-01 2.06173648e-04]
[4.81465717e-05 4.58821829e-04 2.15146201e-05 ... 5.73434571e-03
6.96288990e-01 8.18576980e-02]]
进行预测(精确度可以达到97%):
main.py
from scipy.io import loadmat
from sklearn.metrics import classification_report
import numpy as np
from sigmoid import * # 激活函数data = loadmat('../ex3data1.mat')
X = np.matrix(data['X'])
X = np.insert(X, 0, values=np.ones(X.shape[0]), axis=1) # axis=1即按列插入
y = data['y']
weights = loadmat('ex3weights.mat')
theta1, theta2 = np.matrix(weights['Theta1']), np.matrix(weights['Theta2'])# 神经网络-前向反馈
a1 = X
z2 = a1 * theta1.T
a2 = Sigmoid(z2)
a2 = np.insert(a2, 0, values=np.ones(a2.shape[0]), axis=1) # 加偏置项,值为1
z3 = a2 * theta2.T
a3 = Sigmoid(z3) # h_theta
y_pred = np.argmax(a3, axis=1) + 1 # 每一项的预测值
print(classification_report(y, np.array(y_pred)))
precision recall f1-score support
1 0.97 0.98 0.98 500
2 0.98 0.97 0.98 500
3 0.98 0.96 0.97 500
4 0.97 0.97 0.97 500
5 0.97 0.98 0.98 500
6 0.98 0.99 0.98 500
7 0.98 0.97 0.97 500
8 0.98 0.98 0.98 500
9 0.97 0.96 0.96 500
10 0.98 0.99 0.99 500accuracy 0.98 5000
macro avg 0.98 0.98 0.98 5000
weighted avg 0.98 0.98 0.98 5000
相关文章:

Machine Learning-Ex3(吴恩达课后习题)Multi-class Classification and Neural Networks
目录 1. Multi-class Classification 1.1 Dataset 1.2 Visualizing the data 1.3 Vectorizing Logistic Regression 1.3.1 Vectorizing the cost function(no regularization) 1.3.2 Vectorizing the gradient(no regularization&#…...

【Java】SpringBoot事务回滚规则
SpringBoot事务回滚规则SpringBoot事务回滚规则SpringBoot事务回滚规则 在SpringBoot中,如果一个方法被声明为Transactional,则会开启一个事务。如果这个方法中的任何一个步骤失败了(比如抛出了异常),则该事务将会回滚…...
使用cocopod就那么容易
第一节、配置coopod 打开终端替换ruby镜像源,系统自带的镜像源(gem sources --remove https://rubygems.org/)被墙挡住了或者(https://ruby.taobao.org/)已过期。需替换成新的镜像源。 1).先查看已有的镜像是否是:ht…...

第14届蓝桥杯C++B组省赛
文章目录A. 日期统计B. 01 串的熵C. 冶炼金属D. 飞机降落E. 接龙数列F. 岛屿个数G. 子串简写H. 整数删除I. 景区导游J. 砍树今年比去年难好多 Update 2023.4.10 反转了,炼金二分没写错,可以AC了 Update 2023.4.9 rnm退钱,把简单的都放后面…...
3:方法的重写)
面向对象编程(进阶)3:方法的重写
目录 3.1 方法重写举例 Override使用说明: 3.2 方法重写的要求 3.3 小结:方法的重载与重写 (1)同一个类中 (2)父子类中 3.4 练习 父类的所有方法子类都会继承,但是当某个方法被继承到子类…...
2023年第十四届蓝桥杯Java_大学B组真题
Java_B组试题 A: 阶乘求和试题 B: 幸运数字试题 C: 数组分割试题 D: 矩形总面积试题 E: 蜗牛试题 F: 合并区域试题 G: 买二赠一试题 H: 合并石子试题 I: 最大开支试题 J: 魔法阵【考生须知】 考试开始后,选手首先下载题目,并使用考场现场公布的解压密码解…...

APIs --- DOM事件进阶
1. 事件流 事件流指的是事件完整执行过程中的流动路径 任意事件被触发时总会经历两个阶段:【捕获阶段】和【冒泡阶段】 事件捕获 概念:从DOM的根元素开始去执行对应的事件(从外到里) 捕获阶段是【从父到子】的传导过程 代码&…...

awk命令详解以及使用方法
awk命令详解以及使用方法 awk 是一种文本处理工具,它可以逐行扫描文本文件,根据用户指定的规则进行匹配和处理,并输出结果。awk 的名称来自于三位创始人 Alfred Aho、Peter Weinberger 和 Brian Kernighan 的首字母缩写。 awk 通常用于处理以…...
vue-router3.0处理页面滚动部分源码分析
在使用vue-router3.0时候,会发现不同的路由之间来回切换,会滚动到上次浏览的位置,今天就来看看这部分的vue-router中的源码实现。 无论是基于hash还是history的路由切换,都对滚动进行了处理,这里分析其中一种即可。 无…...

走心Python实战应用:【requests+re 模块】快速下载原shen图片
人生苦短,我用python 这次给大家带来的是模块实战 以便大家理解学习 觉得写的好的话,可以给我多多点赞鸭~ 走心Python实战应用:【requestsre 模块】快速下载原shen图片一、理解Python requests 模块二、requests 方法三、ruqusets 模块实战…...

Comparable和Comparator的使用
在Java中,Comparable和Comparator都是用来实现对象排序的接口。 Comparable Comparable是一个内部比较器接口,它允许在类定义时对该类进行自然排序。当实现了Comparable接口的类的对象列表被传递给Collections.sort()方法时,该方法将使用该…...

【OJ每日一练】1121 - 耐摔指数
文章目录 一、题目🔸题目描述🔸输入输出🔸样例二、思路解析三、代码参考作者:KJ.JK🌈 🌈 🌈 🌈 🌈 🌈 🌈 🌈 🌈 🌈 🌈 🌈 🌈 🍂个人博客首页: KJ.JK 💖系列专栏:OJ每日一练 一、题目 🔸题目描述 x星球的居民脾气不太好,但好在他…...
vue项目Agora声网实现一对一视频聊天Demo示例(Agora声网实战及agora-rtc-vue使用,新增在线预览地址)
最终效果 在线预览地址 一、声网简介---->请查看官网 二、声网注册---->请自行百度(创建音视频连接需要在Agora注册属于您的appid) 三、具体实现视频聊天步骤 1、 实现音视频通话基本逻辑 1、创建对象 调用 createClient 方法创建 AgoraRTCCli…...
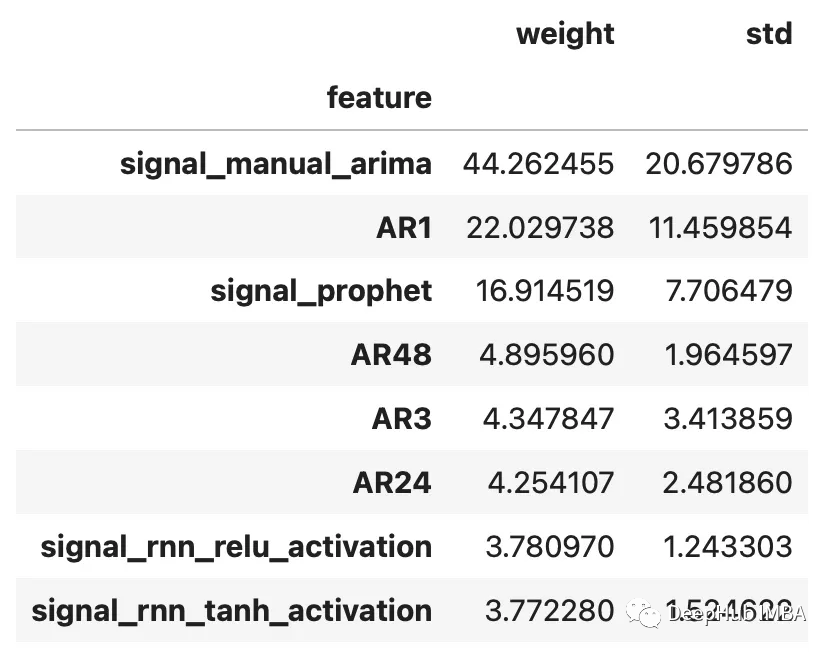
集成时间序列模型提高预测精度
使用Catboost从RNN、ARIMA和Prophet模型中提取信号进行预测 集成各种弱学习器可以提高预测精度,但是如果我们的模型已经很强大了,集成学习往往也能够起到锦上添花的作用。流行的机器学习库scikit-learn提供了一个StackingRegressor,可以用于…...
(详细)《美国节日》:某月的第几个星期几
目录 一、题目描述: 二、思路: 1、给定 年月日,如何知道这天是星期几? 2、已知这个月的第一天是星期几,如何知道第三个星期一是几号? 3、最后一个星期一 三、思路总结 四、代码 一、题目描述…...

架构设计的历史背景
架构设计的历史背景 在探讨架构设计的历史背景时,了解软件开发进化的历史是一个重要的起点。了解软件开发的演变过程可以帮助我们更好地理解架构设计的起源和发展。现在,让我们来简要回顾一下软件开发的历史,并探索软件架构出现的背景。 首先…...
C#,初学琼林(06)——组合数的算法、数据溢出问题的解决方法及相关C#源代码
1 排列permutation 排列,一般地,从n个不同元素中取出m(m≤n)个元素,按照一定的顺序排成一列,叫做从n个元素中取出m个元素的一个排列(permutation)。特别地,当mn时,这个排列被称作全…...

MySQL数据库——绘制E-R图:数据库概要设计阶段
在MySQL数据库的概要设计阶段,绘制E-R图是非常重要的一步。E-R图(实体关系图)是一种图形化的工具,用于描述数据库中实体之间的关系。 以下是在MySQL数据库概要设计阶段绘制E-R图的步骤: 确定实体:在MySQL数…...

对类和对象的理解
对象:对象是人们要进行研究的任何事物,它不仅能表示具体的事物,还能表示抽象的规则、计划或事件。对象具有状态,一个对象用数据值来描述它的状态。对象还有操作,用于改变对象的状态,对象及其操作就是对象的…...

edge-tts微软文本转语音库,来听听这些语音是否很熟悉?
上期图文教程,我们分享了Azure机器学习的文本转语音的账号申请与API申请的详细步骤,也介绍了基于python3实现Azure机器学习文本转语音功能的代码实现过程,虽然我们可以使用Azure账号免费提供一年的试用期,但是毕竟是要付费的,我们的API也无法长期使用,好在微软发布了edge…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...

小木的算法日记-多叉树的递归/层序遍历
🌲 从二叉树到森林:一文彻底搞懂多叉树遍历的艺术 🚀 引言 你好,未来的算法大神! 在数据结构的世界里,“树”无疑是最核心、最迷人的概念之一。我们中的大多数人都是从 二叉树 开始入门的,它…...
