(详细)《美国节日》:某月的第几个星期几
目录
一、题目描述:
二、思路:
1、给定 年月日,如何知道这天是星期几?
2、已知这个月的第一天是星期几,如何知道第三个星期一是几号?
3、最后一个星期一
三、思路总结
四、代码
一、题目描述:
美国节日 美国节日
和中国的节日不同,美国的节假日通常是选择某个月的第几个星期几这种形式,因此每一年的放假日期都不相同。具体规则如下:
* 1月1日:元旦
* 1月的第三个星期一:马丁·路德·金纪念日
* 2月的第三个星期一:总统节
* 5月的最后一个星期一:阵亡将士纪念日
* 7月4日:美国国庆
* 9月的第一个星期一:劳动节
* 11月的第四个星期四:感恩节
* 12月25日:圣诞节
现在给出一个年份,请你帮忙生成当年节日的日期。
输入描述:
输入包含多组数据,每组数据包含一个正整数year(2000≤year≤9999)。输出描述:
对应每一组数据,以“YYYY-MM-DD”格式输出当年所有的节日日期,每个日期占一行。每组数据之后输出一个空行作为分隔。
示例1:
输入:
2014
2013
输出:
2014-01-01
2014-01-20
2014-02-17
2014-05-26
2014-07-04
2014-09-01
2014-11-27
2014-12-252013-01-01
2013-01-21
2013-02-18
2013-05-27
2013-07-04
2013-09-02
2013-11-28
2013-12-25
二、思路:
每年的第一天的星期几是不固定的,进而每个月的第一天是星期几也是不固定的,因此我们需要计算。
我们要求解这个题目主要有两个大问题需要考虑:
- 1、给定 年月日 ,如何知道这天是星期几?
- 2、已知这个月的第一天是星期几,如何知道第三个星期一(第一个星期一...)是几号?
1、给定 年月日,如何知道这天是星期几?
我们需要找到一个基准值。
例如:已知今天是 2023-4-11 星期二,问2023-4-20 是星期几?
(2023-4-20) - (2023-4-11)= 9 天 ,因此 9 % 7 = 2,则2023-4-20就是 (2 + 2)% 7 = 4

该题目中,我们以公元前1年12月31日作为基准值,已知这一天是星期7 。
(年 - 月 - 日)-(0000-12-31)= 一共多少个整年的天数 + 最后一年的天数。
例如:找 2023年 4月 11日是星期几,我们先要知道从2023-4-11到 0000-12-31 一共有多少天。
(2023-4-11)-(0000-12-31)= (0000~2023)中间年的天数 + 2023开始后面的天数(不够一年)
(1)要计算(0000~2023)中间年的天数:
0000-12-31是最后一天,因此 2023 - 0001 是中间差的年数,即(2023 - 1),说明中间有2022个年份,因此(年 - 1)。我们这里先默认这些中间的年份都是平年,因此如果有闰年的话,整体上 加上 闰年的个数 * 1(因为闰年比平年要多一天)即可。
因此公式就转化成:
(年 - 月 - 日)-(0000-12-31)= (年 - 1)* 365 + 中间闰年个数 * 1 + 最后一年的天数。
① 计算中间闰年的个数,[1,y)有多少个闰年:
闰年:能被400整除 || 能被4整除但不能被100整除
以上面的例子来说:
(2023-4-11)-(0000-12-31) = (2023-1)*365 + 中间闰年个数*1 + 最后一年的天数
现在已知有 2022个年,要计算这2022个年中有多少年是闰年。
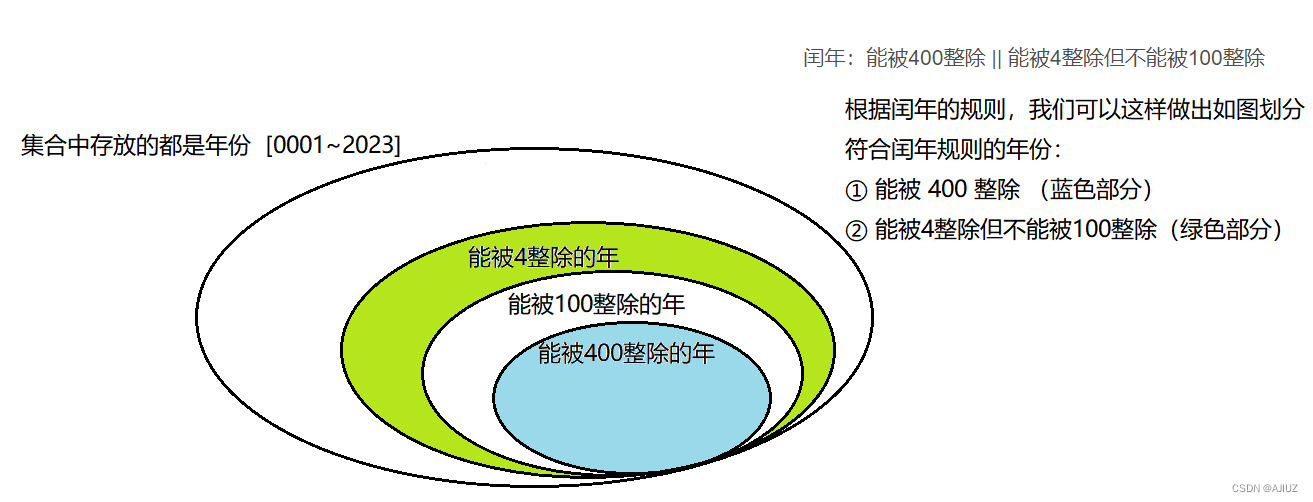
要计算这2022个年中有多少个年就可以写成:
2022 / 4 - 2022 / 100 + 2022 / 400
即:可以被 4 整除的年数(y - 1)/ 4 减去 可以被100整除的年数(y - 1)/ 100 加上 可以被400整除的年数(y - 1)/ 400 。
注意:计算[ 1 , 2022 ]中有多少个数可以被 4 整除,可以直接用 2022 / 4 即可。

此时公式就转化为:(年月日用 y-m-d替换)
(y-m-d)-(0000-12-31)= (y - 1)* 365 +(y - 1)/ 4 - (y - 1)/ 100 + (y - 1) / 400 + 最后一年的天数
因为星期一到星期天是7天一循环,而 对于 365 来说,本身就包含了很多个 7 的整数倍了,因此这里面的所有的 7 的整数倍 都可以无视掉。
365 % 7 = 1,364为 7 的整数倍,对应到星期的循环中,相当于又到星期一(最开始的时候)了。因此我们可以用 1 替换 365,最后计算的效果是一样的。
公式就变成了:
(y-m-d)-(0000-12-31)= (y - 1) +(y - 1)/ 4 - (y - 1)/ 100 + (y - 1) / 400 + 最后一年的天数
② 最后一年的天数 :
每个月的天数是固定的(假设是平年),因此我们可以得到一个存放每个月天数的数组。
假设要求 6 月 8日 在这年里是多少天,就要求 [1,5] 月的天数是多少,最后加上 6 。此时还要判断该年是否是闰年,如果是闰年,且要求的日期在 2 月之后(2月之前闰年和平年没区别),还要在总天数后 + 1 。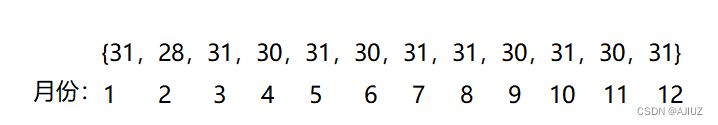
因此:
最后一年的天数 = 经过完整的月的天数之和 + d + (闰年?1:0) (判断是否在 2 月之后)
2、已知这个月的第一天是星期几,如何知道第三个星期一是几号?
以题中 求第三个星期一为例。
已知4月1日是星期五,求 4月的第三个星期一是几号?
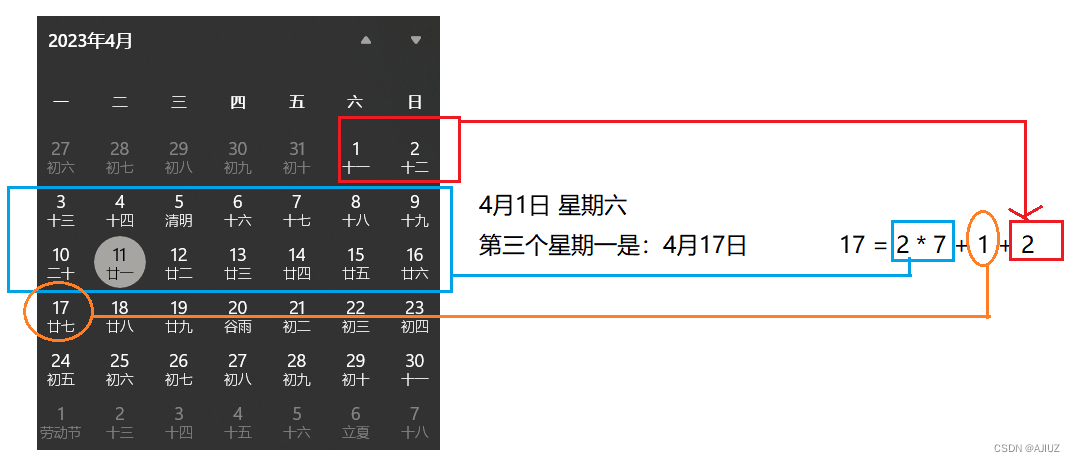
依次类推,如果4月1日是星期天、星期一、星期二......

如果求第一个星期一:
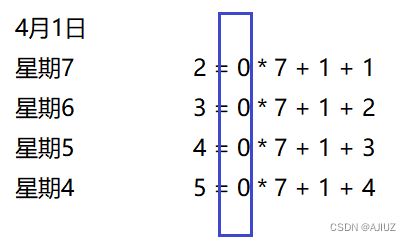
因此我们可以总结出一个规律:
假设要找第 n 个星期 x :
(n - 1) * 7 +1 + (7 - w + x) % 7
3、最后一个星期一
找到下个月的1日的星期数。
题目中找5月的最后一个星期一,因此我们找到该年的 6月1日是星期几,然后将6月1日看做 5月32日。
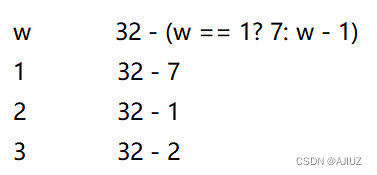
三、思路总结
题目分析:
1、给定年月日,如何知道这一天是星期几?
(1)先要知道给定的年月日,距离基准值(0000-12-31)的天数
天数:(y-1) + (y-1)/4 - (y-1)/100 + (y-1)/400 + 最后一年的天数
最后一年的天数:经过的完整的月的天数 + d + (闰年?1:0)
(2)知道了距离基准值的天数,根据基准值(0000-12-31 星期 7),计算是星期几
星期几 = (天数 % 7) == 0 ? 7:(天数 % 7)
因为基准是 7 1 2 3 4 5 6 ,因此当 天数 % 7为 0的时候,就是第一个数字 7,而其他的来说(天数 % 7)刚好算出来的数字就对应了星期几。
2、已知1日是星期w,计算第n个星期x:
(n - 1) * 7 +1 + (7 - w + x) % 7
3、已知5月1日是星期w,计算最后一个星期一
32 - (w == 1? 7 : w - 1)
4、输入输出处理
题目中输出的日期形式:2013-01-01,用printf来格式化输出时,要用 %02d 来表示后面"01"的形式。
%d :正常输出十进制数 。
%Yd:十进制数,输出 Y 位。如果本身大于 Y 位,正常输出。
%XYd:十进制数,输出 Y 位,不足 Y 位就补 X 。如果本身大于 Y 位,正常输出。
%d:十进制数正常输出 。
%2d:十进制数,输出 2 位。如果本身大于 2 位,正常输出。
%02d :十进制数,输出 2 位,不足 2 位就补 0 。如果本身大于 2 位,正常输出。
四、代码
import java.util.Scanner;/*** Created with IntelliJ IDEA.* Description:美国节日* 1月的第三个星期一:马丁·路德·金纪念日* 2月的第三个星期一:总统节* 5月的最后一个星期一:阵亡将士纪念日* 7月4日:美国国庆* 9月的第一个星期一:劳动节* 11月的第四个星期四:感恩节* 12月25日:圣诞节* User: WangWZ* Date: 2023-04-11* Time: 15:39*/
public class Main2 {//判断是否是闰年private static boolean isLeapYear(int y) {return ((y % 400 == 0)||(y % 4 == 0 && y % 100 != 0));}//判断最后一年的天数private static int lastDays(int y, int m, int d) {int[] arr = {31,28,31,30,31,30,31,31,30,31,30,31};int ans = 0;for (int i = 0; i < m - 1; i++) {ans += arr[i];}//最后计算不满的一个月的天数//需要进行闰年的判断ans += d;if(m > 2 && isLeapYear(y)) {ans += 1;}return ans;}//已知年月日,根据基准(0000-12-31 星期 7)判断有多少天private static int nDays(int y, int m, int d){return (y - 1) + (y - 1)/4 - (y - 1)/100 + (y - 1)/400 + lastDays(y,m,d);}//1.给定 年月日 ,如何知道这天是星期几?public static int week(int y, int m, int d) {//给定年月日,要确定这天是星期几://1.先要知道给定的年月日,距离基准值(0000-12-31)的天数//天数:(y-1) + (y-1)/4 - (y-1)/100 + (y-1)/400 + 最后一年的天数//最后一年的天数:经过的完整的月的天数 + d + (闰年?1:0)//2.知道了距离基准值的天数,根据基准值(0000-12-31 星期 7),计算是星期几//星期几 = (天数 % 7) == 0 ? 7:(天数 % 7)//因为基准是 7 1 2 3 4 5 6 ,因此当 天数 % 7为 0的时候,就是第一个数字 7,//而其他的来说(天数 % 7)刚好算出来的数字就对应了星期几int days = nDays(y,m,d);int w = days % 7;return (w == 0)?7:w;}//2.已知这个月的第一天是星期几,如何知道第三个星期一(第一个星期一...)是几号//(1)已知 1日是星期 w,计算第 n个星期 x是几号private static int m1(int n, int x,int w) {return (n - 1)* 7 + 1 + (7 - w + x)% 7;}//(2)根据 6月 1日是星期w,求 5月的最后一个星期一 是几号private static int m2(int w) {return 32-((w == 1)?7:w - 1);}public static void main(String[] args) {Scanner scanner = new Scanner(System.in);while(scanner.hasNextInt()) {int y = scanner.nextInt();//1月1日:元旦System.out.printf("%d-01-01\n", y);//1月的第三个星期一:马丁·路德·金纪念日int w = week(y,1,1);System.out.printf("%d-01-%02d\n", y,m1(3,1,w));//2月的第三个星期一:总统节w = week(y,2,1);System.out.printf("%d-02-%02d\n", y,m1(3,1,w));//5月的最后一个星期一:阵亡将士纪念日w = week(y,6,1);System.out.printf("%d-05-%02d\n",y,m2(w));//7月4日:美国国庆System.out.printf("%d-07-04\n", y);//9月的第一个星期一:劳动节w = week(y,9,1);System.out.printf("%d-09-%02d\n", y,m1(1,1,w));//11月的第四个星期四:感恩节w = week(y,11,1);System.out.printf("%d-11-%02d\n",y,m1(4,4,w));//12月25日:圣诞节System.out.printf("%d-12-25\n",y);System.out.println();}}
}
相关文章:
(详细)《美国节日》:某月的第几个星期几
目录 一、题目描述: 二、思路: 1、给定 年月日,如何知道这天是星期几? 2、已知这个月的第一天是星期几,如何知道第三个星期一是几号? 3、最后一个星期一 三、思路总结 四、代码 一、题目描述…...

架构设计的历史背景
架构设计的历史背景 在探讨架构设计的历史背景时,了解软件开发进化的历史是一个重要的起点。了解软件开发的演变过程可以帮助我们更好地理解架构设计的起源和发展。现在,让我们来简要回顾一下软件开发的历史,并探索软件架构出现的背景。 首先…...
C#,初学琼林(06)——组合数的算法、数据溢出问题的解决方法及相关C#源代码
1 排列permutation 排列,一般地,从n个不同元素中取出m(m≤n)个元素,按照一定的顺序排成一列,叫做从n个元素中取出m个元素的一个排列(permutation)。特别地,当mn时,这个排列被称作全…...

MySQL数据库——绘制E-R图:数据库概要设计阶段
在MySQL数据库的概要设计阶段,绘制E-R图是非常重要的一步。E-R图(实体关系图)是一种图形化的工具,用于描述数据库中实体之间的关系。 以下是在MySQL数据库概要设计阶段绘制E-R图的步骤: 确定实体:在MySQL数…...

对类和对象的理解
对象:对象是人们要进行研究的任何事物,它不仅能表示具体的事物,还能表示抽象的规则、计划或事件。对象具有状态,一个对象用数据值来描述它的状态。对象还有操作,用于改变对象的状态,对象及其操作就是对象的…...

edge-tts微软文本转语音库,来听听这些语音是否很熟悉?
上期图文教程,我们分享了Azure机器学习的文本转语音的账号申请与API申请的详细步骤,也介绍了基于python3实现Azure机器学习文本转语音功能的代码实现过程,虽然我们可以使用Azure账号免费提供一年的试用期,但是毕竟是要付费的,我们的API也无法长期使用,好在微软发布了edge…...

MySQL更换存储引擎
要更换 MySQL 5.7 中某个表的存储引擎,可以使用以下的 SQL 命令: sql复制代码 ALTER TABLE table_name ENGINEengine_name; 其中,table_name 是需要更换存储引擎的数据表名称,engine_name 则是需要更换成的新存储引擎名称。 举…...

filebeat收集不规则多行日志
现环境有多行日志输出内容和格式不确定,合并后使用grok默认正则无法收集,需要自己编写正则 日志内容如下: ERROR|2023-04-06 14:27:52|helper|test|http|/api/ad/listBanner|1d60fff861bqwe4b0397be554141eb 127.0.0.1|1b4429-5adb-44d4-acf…...
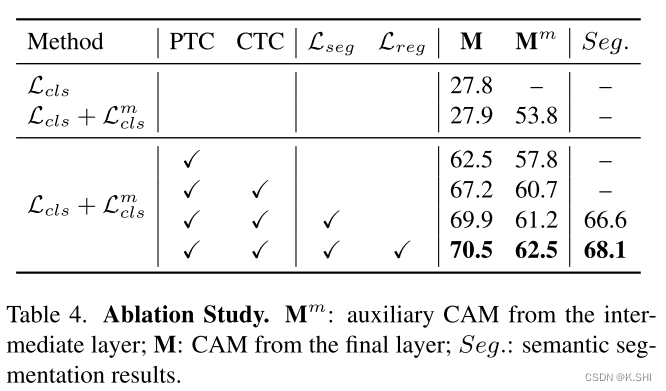
Token Contrast for Weakly-Supervised Semantic Segmentation
文章来源:[CVPR2023] Keywords:Weakly-Supervised Semantic Segmentation(WSSS);over-smoothing; ViT 一、本文提出的问题以及解决方案: 本文解决了over-smoothing问题,该问题其实是在之前的GCN网络中提出…...

Jenkins运行在docker中使用Maven构建Java应用程序
这篇笔记是Jenkins入门教程使用Maven构建Java应用程序的一个补充说明,因为我照着文档操作的过程中遇到不少问题,遂一一做个笔记。 我的主机是Windows 11,安装的docker是Docker Desktop 4.18.0。 第一点,在Windows里执行docker命…...
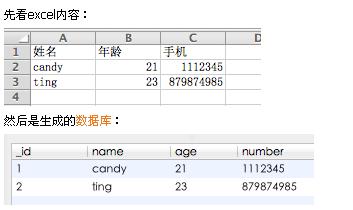
将excel导入到sqlite的方法代码
Python实现excel转sqlite的方法,具体如下: Python环境的安装配置就不说了,个人喜欢pydev的开发环境。 python解析excel需要使用第三方的库,这里选择使用xlrd 下面是源代码: #!/usr/bin/python # encodingutf-8 Creat…...

Redis主从复制、哨兵和集群部署
文章目录一、主从复制1、主从复制-哨兵-集群2、主从复制的概念3、主从复制的作用4、主从复制流程5、部署Redis 主从复制步骤6、实例操作:部署Redis 主从复制二、哨兵模式1、哨兵模式的原理2、哨兵模式的作用3、哨兵结构由两部分组成,哨兵节点和数据节点4…...

protobuf序列化
文章目录protubufprotobuf序列化protobuf的原理定义message编译message文件应用protobufMessage 基本用法Message 嵌套使用protubuf protobuf序列化 protobuf是一种比json和xml等序列化工具更加轻量和高效的结构化数据存储格式,性能比json和xml真的强很多ÿ…...
更新时无冲突的情况(阁瑞钛伦特软件-九耶实训)
大多数使用“与资源库同步”菜单的目的是想查看本地和远程资源的差异,并不想将本地的内容进行更新。 而“更新”菜单则不然,它的主要作用是将远程仓库中的内容下载到本地,以使本地的版本内容和仓库中的内容一致。 Step01:复用前…...

3.4 函数的单调性和曲线的凹凸性
学习目标: 如果我要学习函数的单调性和曲线的凹凸性,我会采取以下几个步骤: 理解概念和定义:首先,我会学习单调性和凹凸性的定义和概念。单调性是指函数的增减性质,可以分为单调递增和单调递减;…...

LeetCode 404. 左叶子之和 | C++语言版
LeetCode 404. 左叶子之和 | C语言版LeetCode 404. 左叶子之和题目描述解题思路思路一:使用递归代码实现运行结果参考文章:思路二:减少遍历节点数代码实现运行结果参考文章:LeetCode 404. 左叶子之和 题目描述 题目地址…...

arm架构安装Rancher并导入k8s集群解决Error: no objects passed to apply
Rancher介绍 Rancher 2.0-2.4版本 是一个开源的企业级容器管理平台。通过Rancher,企业再也不必自己使用一系列的开源软件去从头搭建容器服务平台。Rancher提供了在生产环境中使用的管理Docker和Kubernetes的全栈化容器部署与管理平台。 Rancher 2.5版本 是为使用容…...
安装PaddleSpeech
github地址https://github.com/PaddlePaddle/PaddleSpeech 创建虚拟环境 conda create -p E:\Python\envs\nlppaddle python3.7 # conda create -p E:\Python\envs\speechstu python3.8激活虚拟环境 conda activate E:\Python\envs\nlppaddle # conda activate E:\Python\…...
UE “体积”的简单介绍
目录 一、阻挡体积 二、摄像机阻挡体积 三、销毁Z体积 四、后期处理体积 一、阻挡体积 你可以在静态网格体上使用阻挡体积替代碰撞表面,比如建筑物墙壁。这可以增强场景的可预测性,因为物理对象不会与地面和墙壁上的凸起细节相互作用。它还能降低物理模…...

微信 JAVA SDK 封装
weixin-popular 微信 JAVA SDK,是微信平台(公众平台、开放平台、商户平台、服务商平台)接口服务的JAVA 实现,开发 严格按照官方技术文档,合理划分包名、定义字段及方法,能胜任任何微信相关的业务。 使用建…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...
