3.4 函数的单调性和曲线的凹凸性
学习目标:
如果我要学习函数的单调性和曲线的凹凸性,我会采取以下几个步骤:
-
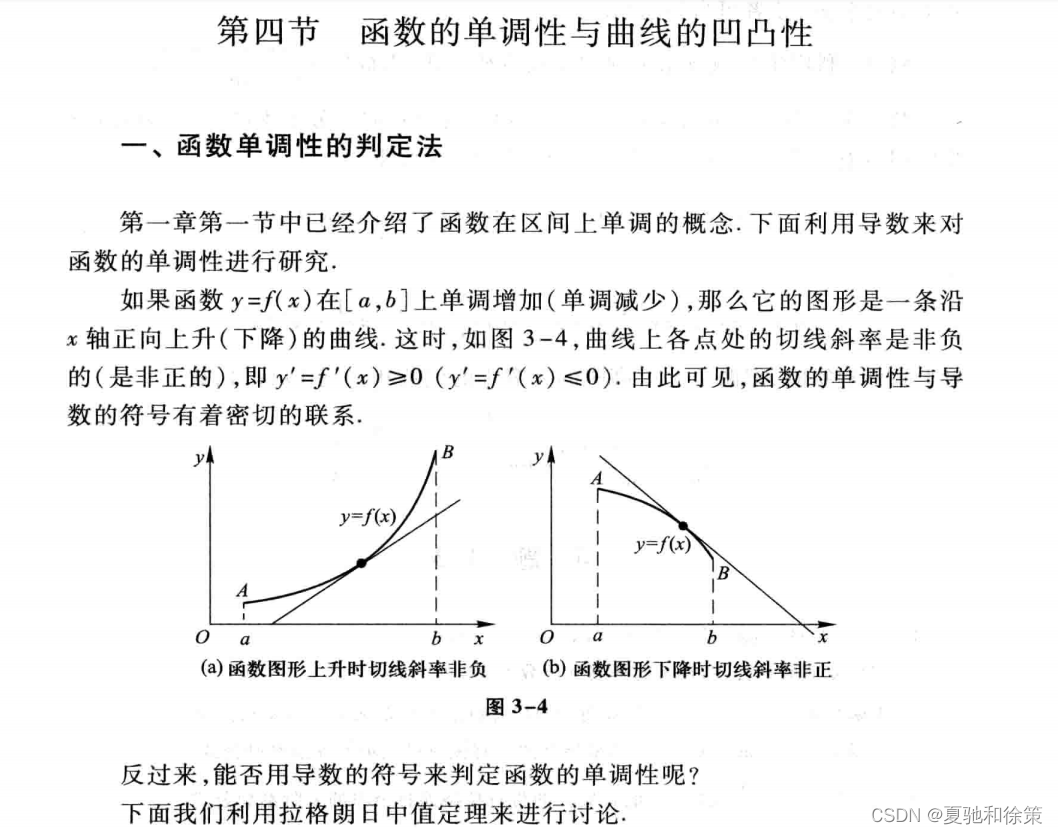
理解概念和定义:首先,我会学习单调性和凹凸性的定义和概念。单调性是指函数的增减性质,可以分为单调递增和单调递减;凹凸性是指函数的弯曲程度,可以分为凹和凸。我会理解这些概念的意义和特点,以及如何通过图像来判断函数的单调性和凹凸性。
-
掌握判断方法:其次,我会掌握判断函数单调性和凹凸性的方法。例如,函数的导数可以用来判断函数的单调性和凹凸性,对于单峰函数或双峰函数,还可以通过二阶导数的符号来判断其凹凸性。我会学习这些方法的原理和应用,通过练习来提高自己的判断能力。
-
熟练运用:接着,我会通过练习来熟练运用判断函数单调性和凹凸性的方法。我会选取不同类型的函数,例如多项式函数、三角函数、指数函数等,来练习如何判断它们的单调性和凹凸性。我会注重练习,通过不断地尝试和纠错,提高自己的判断水平和准确性。
-
应用于问题:最后,我会应用所学的知识来解决实际问题。例如,在最优化问题中,函数的单调性和凹凸性可以用来确定函数的极值点和拐点,从而帮助我们找到最优解。我会通过实际问题的练习来应用所学的知识,加深自己对单调性和凹凸性的理解和掌握。





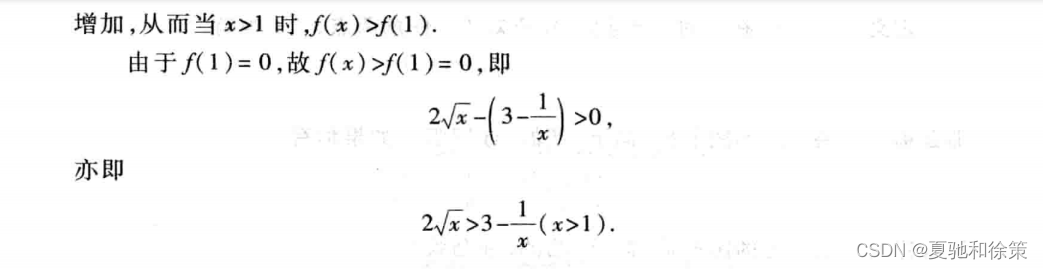 我的理解:
我的理解:
函数的单调性是指函数的增减规律。在数学中,通常分为严格单调递增、严格单调递减、非严格单调递增和非严格单调递减四种情况。下面是函数单调性的判断方法:
-
导数法:如果函数在定义域内的导数大于 0,则函数在该区间内严格单调递增;如果导数小于 0,则函数在该区间内严格单调递减。如果导数等于 0,则需要进一步分析。
-
二阶导数法:如果函数在定义域内的二阶导数大于 0,则函数在该区间内非严格单调递增;如果二阶导数小于 0,则函数在该区间内非严格单调递减。如果二阶导数等于 0,则需要进一步分析。
-
利用单调性的定义:如果函数在一个区间内单调递增,那么在这个区间内任意两个点的函数值都有 f(x1) < f(x2) 成立。反之,如果函数在一个区间内单调递减,那么在这个区间内任意两个点的函数值都有 f(x1) > f(x2) 成立。
-
图像法:根据函数图像的走势,可以判断函数的单调性。如果函数图像在某个区间内向上倾斜,则函数在该区间内单调递增;如果函数图像在某个区间内向下倾斜,则函数在该区间内单调递减。注意,这种方法只适用于简单的函数图像。
以上是函数单调性的判断方法,根据实际情况和题目要求可以灵活选择。需要注意的是,有些函数并不具备单调性,这时需要特殊分析。






 我的理解:
我的理解:
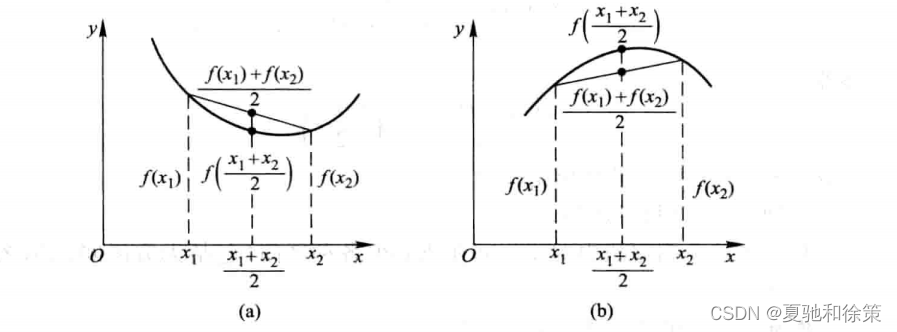
函数的凹凸性是指函数图像的弯曲程度,具体地说,如果函数图像在一个区间内向上弯曲,那么该区间内函数具有凹性;如果函数图像在一个区间内向下弯曲,那么该区间内函数具有凸性。函数的凹凸性分为严格凹函数、严格凸函数、非严格凹函数和非严格凸函数四种情况。
拐点是指函数图像由凹性向凸性或者由凸性向凹性转变的点,即函数的凹凸性发生改变的点。拐点处的二阶导数为 0,但不一定是拐点,还需要根据一阶导数的正负情况来判断。
下面是函数凹凸性和拐点的判断方法:
-
导数法:如果函数在定义域内的二阶导数大于 0,则函数在该区间内具有凸性;如果二阶导数小于 0,则函数在该区间内具有凹性。如果二阶导数等于 0,则需要进一步判断一阶导数的正负情况,如果一阶导数在拐点处发生正向变化,则该点为拐点,且函数从凹性转变为凸性;如果一阶导数在拐点处发生负向变化,则该点为拐点,且函数从凸性转变为凹性。
-
利用函数凹凸性的定义:如果函数在一个区间内具有凸性,那么在该区间内任意两个点的函数值都有 f((x1+x2)/2) < (f(x1) + f(x2))/2 成立。如果函数在一个区间内具有凹性,那么在该区间内任意两个点的函数值都有 f((x1+x2)/2) > (f(x1) + f(x2))/2 成立。如果在某个点上两个式子都成立,那么该点就是拐点。
-
图像法:通过观察函数图像,可以直观地判断函数的凹凸性和拐点。在函数图像上,凹性表现为图像向上弯曲,凸性表现为图像向下弯曲,拐点表现为图像从向上弯曲转变为向下弯曲,或者从向下弯曲转变为向上弯曲的位置。
以上是函数凹凸性和拐点的判断方法,需要根据实际情况和题目要求进行灵活运用。
总结
函数的单调性和曲线的凹凸性是微积分中重要的概念之一,它们与函数的导数、二阶导数等密切相关。下面是它们的重点、难点和易错点:
- 函数的单调性
重点:定义和判断方法。可以利用导数的符号判断函数的单调性。当导数$f'(x)$在定义域上恒大于零时,函数递增;当导数f'(x)在定义域上恒小于零时,函数递减。
难点:拐点。拐点处函数单调性可能发生变化,需要根据二阶导数f''(x)的符号进行判断。
易错点:区间判断。判断函数的单调性时要注意定义域上是否连续,以及是否存在间断点等特殊情况。此外,要注意区间的开闭性和函数值的取值范围等细节。
- 曲线的凹凸性
重点:定义和判断方法。可以利用二阶导数f'(x)的符号判断曲线的凹凸性。
难点:拐点。拐点处曲线的凹凸性可能发生变化,需要根据三阶导数$f'''(x)$的符号进行判断。
易错点:凸区间与凹区间。在某些情况下,曲线的凸凹性可能在同一个区间内交替出现。此外,要注意区间的开闭性和函数值的取值范围等细节。

相关文章:

3.4 函数的单调性和曲线的凹凸性
学习目标: 如果我要学习函数的单调性和曲线的凹凸性,我会采取以下几个步骤: 理解概念和定义:首先,我会学习单调性和凹凸性的定义和概念。单调性是指函数的增减性质,可以分为单调递增和单调递减;…...

LeetCode 404. 左叶子之和 | C++语言版
LeetCode 404. 左叶子之和 | C语言版LeetCode 404. 左叶子之和题目描述解题思路思路一:使用递归代码实现运行结果参考文章:思路二:减少遍历节点数代码实现运行结果参考文章:LeetCode 404. 左叶子之和 题目描述 题目地址…...

arm架构安装Rancher并导入k8s集群解决Error: no objects passed to apply
Rancher介绍 Rancher 2.0-2.4版本 是一个开源的企业级容器管理平台。通过Rancher,企业再也不必自己使用一系列的开源软件去从头搭建容器服务平台。Rancher提供了在生产环境中使用的管理Docker和Kubernetes的全栈化容器部署与管理平台。 Rancher 2.5版本 是为使用容…...
安装PaddleSpeech
github地址https://github.com/PaddlePaddle/PaddleSpeech 创建虚拟环境 conda create -p E:\Python\envs\nlppaddle python3.7 # conda create -p E:\Python\envs\speechstu python3.8激活虚拟环境 conda activate E:\Python\envs\nlppaddle # conda activate E:\Python\…...
UE “体积”的简单介绍
目录 一、阻挡体积 二、摄像机阻挡体积 三、销毁Z体积 四、后期处理体积 一、阻挡体积 你可以在静态网格体上使用阻挡体积替代碰撞表面,比如建筑物墙壁。这可以增强场景的可预测性,因为物理对象不会与地面和墙壁上的凸起细节相互作用。它还能降低物理模…...

微信 JAVA SDK 封装
weixin-popular 微信 JAVA SDK,是微信平台(公众平台、开放平台、商户平台、服务商平台)接口服务的JAVA 实现,开发 严格按照官方技术文档,合理划分包名、定义字段及方法,能胜任任何微信相关的业务。 使用建…...

上海智慧校园视频智能分析算法 yolov7
上海智慧校园视频智能分析算法通过yolov7python网络模型分析技术,上海智慧校园视频智能分析算法对校园内学生打架、翻墙、倒地、异常聚集、攀高等行为实时监测预警。YOLOv7 的发展方向与当前主流的实时目标检测器不同,研究团队希望它能够同时支持移动 GP…...
【树】你真的会二叉树了嘛? --二叉树LeetCode专题
Halo,这里是Ppeua。平时主要更新C语言,C,数据结构算法......感兴趣就关注我吧!你定不会失望。 🌈个人主页:主页链接 🌈算法专栏:专栏链接 我会一直往里填充内容哒! &…...
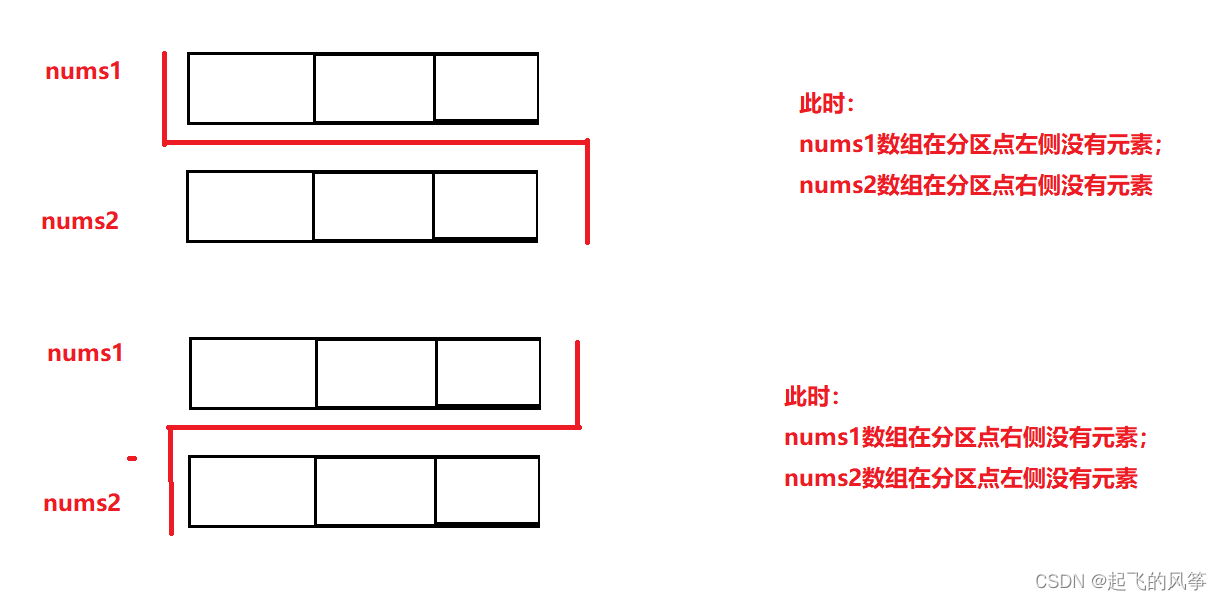
《LeetCode 热题 HOT 100》——寻找两个正序数组的中位数
本期给大家带来的是是《LeetCode 热题 HOT 100》第四题——寻找两个正序数组的中位数的题目讲解!!!() 本文目录 💥题意分析 💥解题思路: 1、直接法 (❌) …...
Unity- 游戏结束以及重启游戏
文章目录游戏结束以及重启游戏建个游戏结束页面编写委托类 游戏主角 以及 ui管理类的脚本重启游戏游戏结束以及重启游戏 思路:利用Canvas创建好覆盖全屏的结束页面,默认关闭。游戏结束时,玩家控制的对象发起委托,ui管理收下委托&…...

NGK BeCu8·11铜合金板材
NGK BeCu811铜合金板材 CB498K、CuSn6Zn4Pb2-B、CC498K、CuSn6Zn4Pb2-C CB494K、CuSn5Pb9-B、CC494K、CuSn5Pb9-C CB495K、CuSn10Pb10-B、CC495K、CuSn10Pb10-C CB496K、CuSn7Pb15-B、CC496K、CuSn7Pb15-C CB497K、CuSn5Pb20-B、CC497K、CuSn5Pb20-C 日本古河连接器专用材料如:…...
电脑突然死机怎么办?正确做法在这!
案例:电脑突然死机怎么办? 【家人们,我刚刚正在做工作报告,突然间电脑就死机了,这可怎么办啊?有什么方法可以快速解决这个问题吗?急急急!】 电脑在使用过程中,有时会出…...
)
基于cell数组的MATLAB仿真(附上完整仿真源码)
MATLAB是一款强大的数学软件,它提供了许多数据结构来存储和处理数据。其中,cell数组是一种非常有用的数据结构,它允许在一个数组中存储不同类型的数据,包括数值、字符串、逻辑值和其他cell数组等。 文章目录简单代码完整仿真源码下…...

电脑蓝屏问题排查
最近电脑安装了最新win10,更新最新的驱动以后,开机几分钟后,会蓝屏重启,报错为: DRIVER_POWER_STATE_FAILURE 下载蓝屏分析工具BlueScreenView 问题出在ntoskrnl.exe bing搜索给出了二种解决方案: 1&a…...
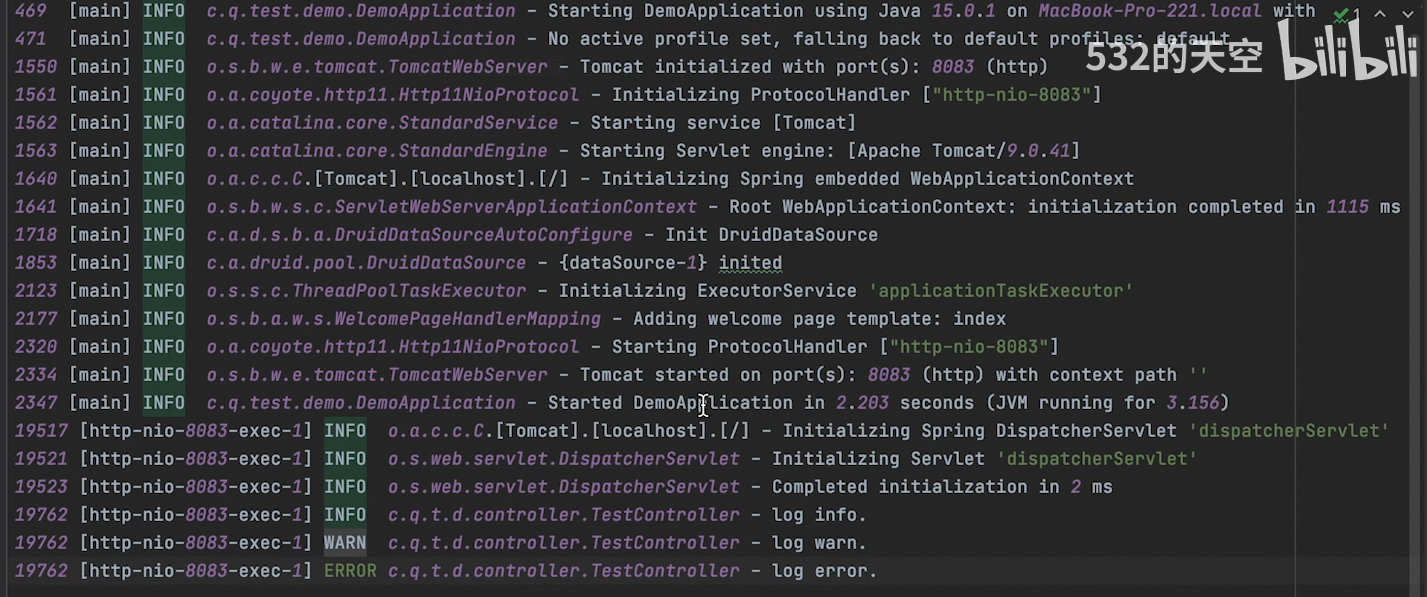
SpringBoot配置slf4j + logback
文章目录日志体系结构在SpringBoot中使用slf4j logback日志框架四种常用的日志输出1. ConsoleAppender2. FileAppender3. RollingFileAppender之TimeBasedRollingPolicy4. RollingFileAppender之SizeAndTimeBasedRollingPolicy日志过滤1. 级别介绍2. 过滤节点filter介绍Spring…...

JAVA——网络编程基本概念
🎉🎉🎉点进来你就是我的人了 博主主页:🙈🙈🙈戳一戳,欢迎大佬指点!人生格言:当你的才华撑不起你的野心的时候,你就应该静下心来学习! 欢迎志同道合的朋友一起加油喔🦾&am…...

[JavaEE]----Spring02
文章目录Spring_day021,IOC/DI配置管理第三方bean1.1 案例:数据源对象管理1.1.1 环境准备1.1.2 思路分析1.1.3 实现Druid管理步骤1:导入druid的依赖步骤2:配置第三方bean步骤3:从IOC容器中获取对应的bean对象步骤4:运行程序1.1.4 实现C3P0管理步骤1:导入C3P0的依赖步…...
笔记本可自行更换CPU、独显了,老外用它手搓了台“PS5”
前面说到微软打算在 Win12 出来前搞出个模块化的Windows:下一个系统不是Win12,微软要复活Win10X。 模块化不用小蝾再过多介绍了,就像积木一样拼在一起组成一个整体。 优势就很明显了,由于每个部分都是单独的模块,更新…...

Linux uart驱动框架
Linux内核提供了标准的UART驱动程序,可以通过以下步骤编写: 首先需要定义一个结构体来存储串口设备数据。在该结构体中,包含一个uart_port结构体,用于与Linux内核通信,并包含一些设备特定的数据(例如波特率…...
第一个禁止ChatGPT的西方国家
意大利成为第一个有效禁止 ChatGPT 的西方国家。 由于可能违反隐私和数据法,该国的数据监管机构已下令开发聊天机器人的 OpenAI 停止运营。 意大利数据保护局 (GPDP) 提到了一些担忧,包括大量收集用户数据和存储以训练 AI 算法。 ChatGPT 是一种大型语…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...

uniapp 实现腾讯云IM群文件上传下载功能
UniApp 集成腾讯云IM实现群文件上传下载功能全攻略 一、功能背景与技术选型 在团队协作场景中,群文件共享是核心需求之一。本文将介绍如何基于腾讯云IMCOS,在uniapp中实现: 群内文件上传/下载文件元数据管理下载进度追踪跨平台文件预览 二…...

9-Oracle 23 ai Vector Search 特性 知识准备
很多小伙伴是不是参加了 免费认证课程(限时至2025/5/15) Oracle AI Vector Search 1Z0-184-25考试,都顺利拿到certified了没。 各行各业的AI 大模型的到来,传统的数据库中的SQL还能不能打,结构化和非结构的话数据如何和…...

Python实现简单音频数据压缩与解压算法
Python实现简单音频数据压缩与解压算法 引言 在音频数据处理中,压缩算法是降低存储成本和传输效率的关键技术。Python作为一门灵活且功能强大的编程语言,提供了丰富的库和工具来实现音频数据的压缩与解压。本文将通过一个简单的音频数据压缩与解压算法…...

