《LeetCode 热题 HOT 100》——寻找两个正序数组的中位数
本期给大家带来的是是《LeetCode 热题 HOT 100》第四题——寻找两个正序数组的中位数的题目讲解!!!()
本文目录
💥题意分析
💥解题思路:
1、直接法 (❌)
2、归并思想 (❌)
①《LeetCode》第88题——合并两个有序数组
3、二分查找(✔️)
整体思想:
题目如下 :👇
给定两个大小分别为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。
算法的时间复杂度应该为 O(log (m+n))
示例 1:
输入:nums1 = [1,3], nums2 = [2]
输出:2.00000
解释:合并数组 = [1,2,3] ,中位数 2示例 2:
输入:nums1 = [1,2], nums2 = [3,4]
输出:2.50000
解释:合并数组 = [1,2,3,4] ,中位数 (2 + 3) / 2 = 2.5
💥题意分析
首先,我们需要注意的一点就是关于本题时间复杂度的要求,本题要求的时间复杂度为 O(log (m+n)) ,这里一定要特别注意!!
其次,我们来对给出的示例给出解释说明,分析题意:
- 首先对于示例一,题目给出了两个数组——nums1和nums2,两个数组的的合并之后且排好序之后为 【1 2 3】,又因为是 double型 输出,此时它的中位数就是 【2.00000】;
- 其次对于示例二,题目给出了两个数组,数组中的元素分别为【1 2】和【3 4】,此时经过排序,我们得到【1 2 3 4】这样的数组,此时数组的长度为偶数,因此中位数的计算就是【(2 + 3) / 2 = 2.5】
💥解题思路:
1、直接法 (❌)
首先,大家拿道题,第一种想到的可能就是直接对这两个数组进行合并在进行排序处理,排完序之后紧接着根据数据长度的奇偶性,我们来判断中位数的到底是n/2还是n/2+1:
代码如下:
class Solution {
public:double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {vector<int>arr;for(auto& e :nums1) {arr.push_back(e);}for(auto& e :nums2) {arr.push_back(e);}sort(arr.begin(),arr.end());int m=arr.size();if( m % 2 == 0){return (double)(arr[m/2]+arr[m/2-1]) /2.0;} else{return arr[m/2];}}
};💨 这种做法可以通过但是却不符合提本题的要求,因为它的时间复杂度就为了 O((m+n)log (m+n)),这样做时间复杂度就取决于排序的代价。因此,这种方法我就此忽略。
2、归并思想 (❌)
其实我们在稍加思考,就可以想到一种优化方法。
💨 我们可以联想到归并排序,这个我想大概应该都学过的。我们不用在进行先合并在sorted,我们可以直接把这两个归并为一个已经排序好的数组。此时这就是双指针的算法,时间复杂度此时为O(m+n)。
这个还可以进行优化,我们不需要对全部进行归并操作,因为我们只关心中位数,因此我们可以计算中位数的下标,假设此时中位数的下表为 k,时间复杂度就为O(k),k的取值取决于数组的长度还是,介于(m+n)/2和 (m+n)/2+1。但是此时依然也不能满足我们题意的 log 级别的时间复杂度的要求.
①《LeetCode》第88题——合并两个有序数组
注意:
- 如果大家对这个排序还不熟悉的小伙伴,我在这里就连带还给出了以下题目的讲解,帮助大家认识 归并排序 思想 :
- 《LeetCode》第88题——合并两个有序数组
题目如下:
给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2,另有两个整数 m 和 n ,分别表示 nums1 和 nums2 中的元素数目。
请你 合并 nums2 到 nums1 中,使合并后的数组同样按 非递减顺序 排列。
注意:
- 最终,合并后数组不应由函数返回,而是存储在数组 nums1 中。为了应对这种情况,nums1 的初始长度为 m + n,其中前 m 个元素表示应合并的元素,后 n 个元素为 0 ,应忽略。nums2 的长度为 n 。
示例 1:
输入:nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3
输出:[1,2,2,3,5,6]
解释:需要合并 [1,2,3] 和 [2,5,6] 。
合并结果是 [1,2,2,3,5,6] ,其中斜体加粗标注的为 nums1 中的元素。示例 2:
输入:nums1 = [1], m = 1, nums2 = [], n = 0
输出:[1]
解释:需要合并 [1] 和 [] 。
合并结果是 [1] 。示例 3:
输入:nums1 = [0], m = 0, nums2 = [1], n = 1
输出:[1]
解释:需要合并的数组是 [] 和 [1] 。
合并结果是 [1] 。
注意,因为 m = 0 ,所以 nums1 中没有元素。nums1 中仅存的 0 仅仅是为了确保合并结果可以顺利存放到 nums1 中。💥题意分析:
- 首先,根据题意,我们可以知道给出了的数据都是已经排好序的了,因此,这就减少了我们的一步操作;
- 紧接着我们可以发现最终是由nums1返回,因此它的空间都足够大
💥解题思路:
1、直接法
- 最容易想到的办法无疑是把数组 nums2 的数据元素全部放入到数组 nums1 的尾部,因此题意告诉我们 nums1 的空间大小为【m+n】,然后直接对整个数组进行排序即可。
代码如下:
class Solution {
public:void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {//此时我们选nums1作为 填充数组,把nums2中元素全部插入到nums1中for(int i=0; i<n; ++i) {nums1[m+i]=nums2[i];}//此时,全部的元素都在nums1数组中了,最后排序输出即可sort(nums1.begin(),nums1.end());}
};性能分析:
- 时间复杂度:跟我们上述暴力解《寻找两个正序数组的中位数》一样,此时 时间复杂度为O((m+n)log(m+n))
- 空间复杂度:因为初始时nums1 的空间长度大小已经为 (m+n)了。因此无需在开辟额外的空间对其进行存放操作,因此 空间复杂度为O(1)
2、归并排序思想
- 如果我们仔细观察这到题很明显就是需要利用 二路归并排序 的思想来做。先确定排序后数组的长度,紧接着比较两数组最后的元素的大小,大的放入新数组的最后一位。(因为本题 nums1 数组的长度是 (m+n),所以我们直接覆盖到 nums1 数组之后即可)
图解:
- 开始时如下图所示:
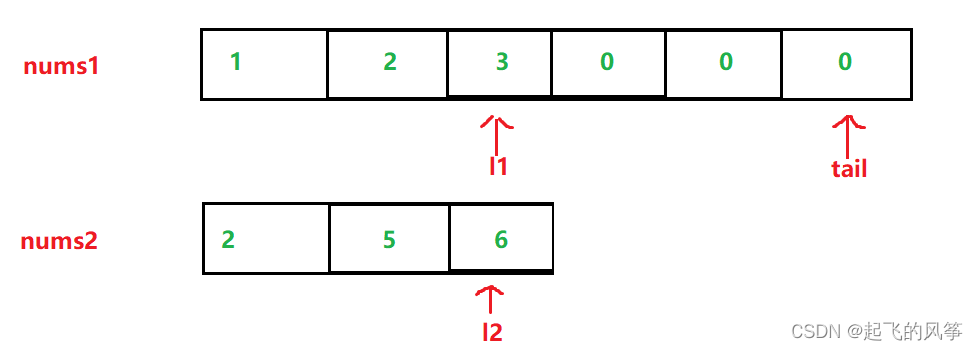
- 第一步,比较 3和6 的大小,此时 6比3 大,因此,把6插入到末尾,同时 l2和tail 两个指针同时往前移动一个位置
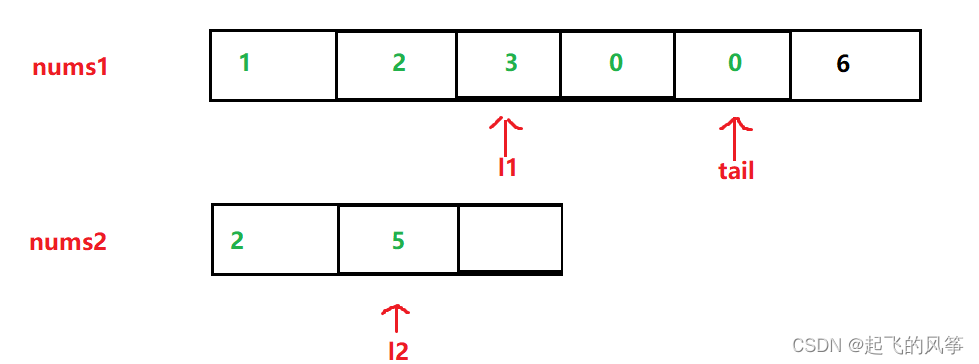
- 第二步:此时在比较 3和5 的大小,发现5比3大,因此同上述操作一样,把 5 插入到 tail指向的位置,同时两个指针在往前移动一位
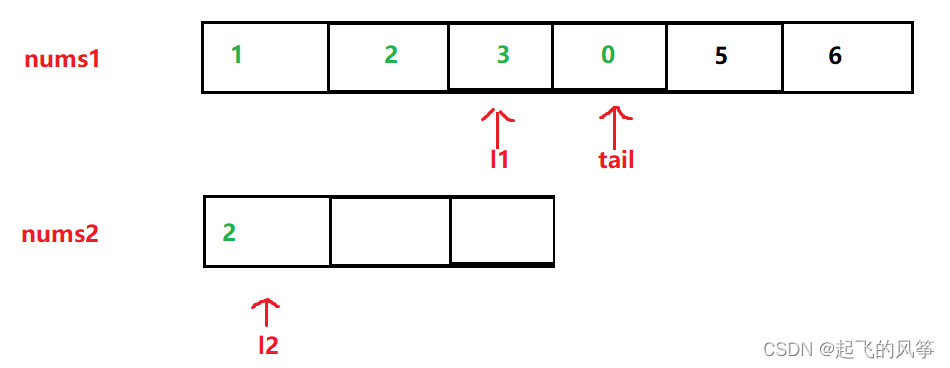
- 第三步:此时比较 3和2 的大小,发现此时 3比2 大,因此,把3插入到 tail指向的位置,同时 tail和 l1 在往前移动一位
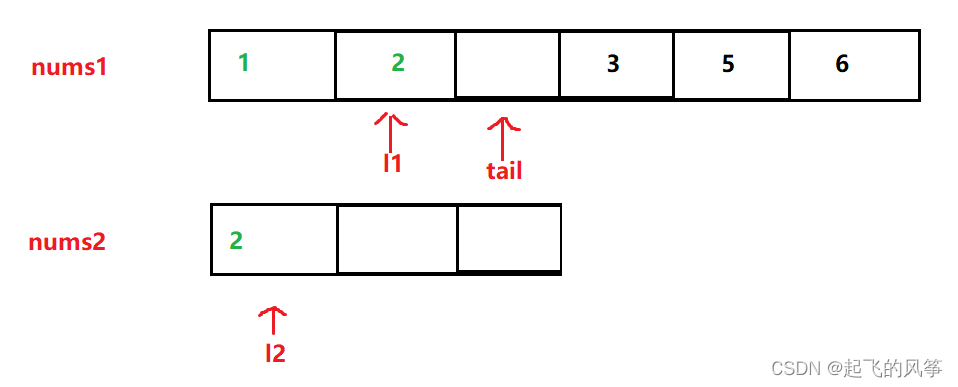
- 第四步:紧接着再次比较 2和2 的大小,发现此时一样大,随便取 l1和l2 位置对应的元素插入到 tail处即可,我们这里是把 l2位置处的 插入到 tail 处。同时移动 l2和tail
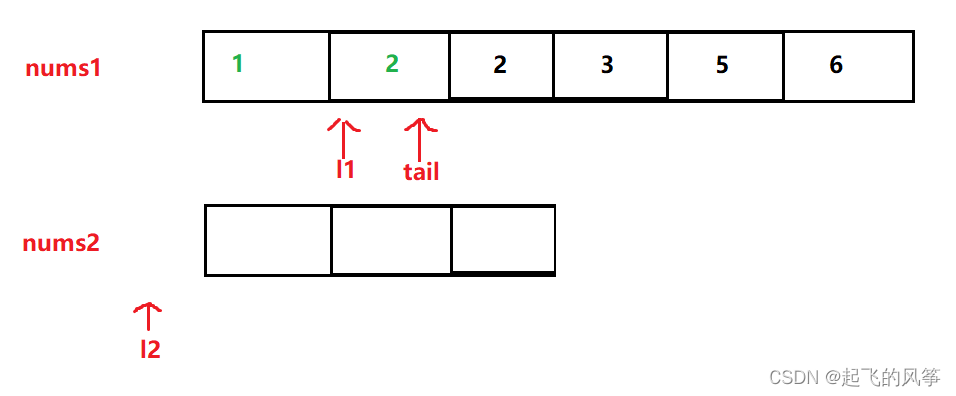
- 第五步:此时 nums2的数据 已经处理完毕了,nums1 中还有数据,只需把 nums1 剩余的元素 放入 tail 所指的位置即可,最后完成排序。
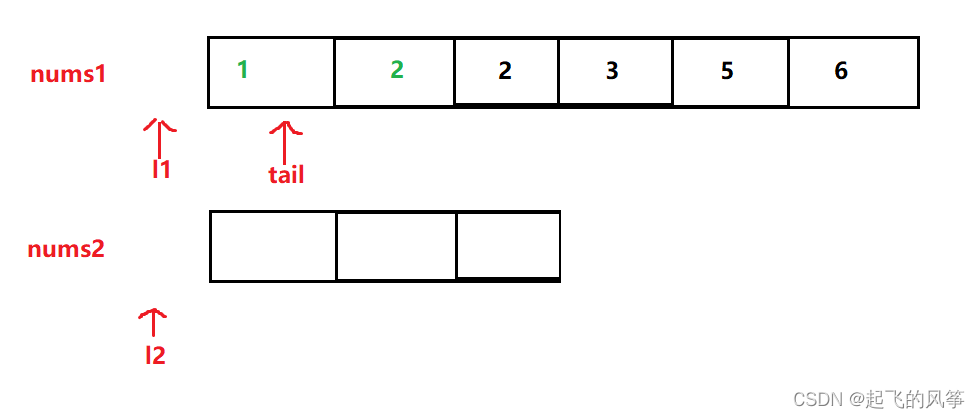
代码如下:
class Solution {
public:void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {int l1 = m - 1;int l2 = n - 1;int tail = m + n - 1;while (l1 >= 0 && l2 >= 0){if (nums1[l1] > nums2[l2]){nums1[tail--] = nums1[l1--];}else{nums1[tail--] = nums2[l2--];}}while (l1 >= 0){nums1[tail--] = nums1[l1--];}while (l2 >= 0){nums1[tail--] = nums2[l2--];}}
};性能分析:
- 时间复杂度:指针移动单调递减,最多移动 m+n 次,因此 时间复杂度为 O(m+n)。
- 空间复杂度:直接对数组 nums1 原地修改,不需要额外空间,因此 空间复杂度为O(1)。
温馨小提示:
我们除了从后往前操作之外,还有从前往后操作。这个任务就交给大家了,原理跟上面讲到的一样的!!!
3、二分查找(✔️)
最后,其实我们可以想到,要想实现 log 级别的时间复杂度,最容易想到的就是采用二分查找的思想。
但是二分查找,我们之前学过的都是对一个数组进行二分查找,本题我们这里有两个数组,因此此题的难度我们可以看到标的是 困难。但是也不要害怕,接下来我带大家分析一波
整体思想:
- 更有效的方法是使用二叉搜索,我们可以在两个数组中找到分区点,使得分区点左侧的元素小于右侧的元素。然后,可以通过取左分区的最大值和右分区的最小值来找到中位数!!!
图解:
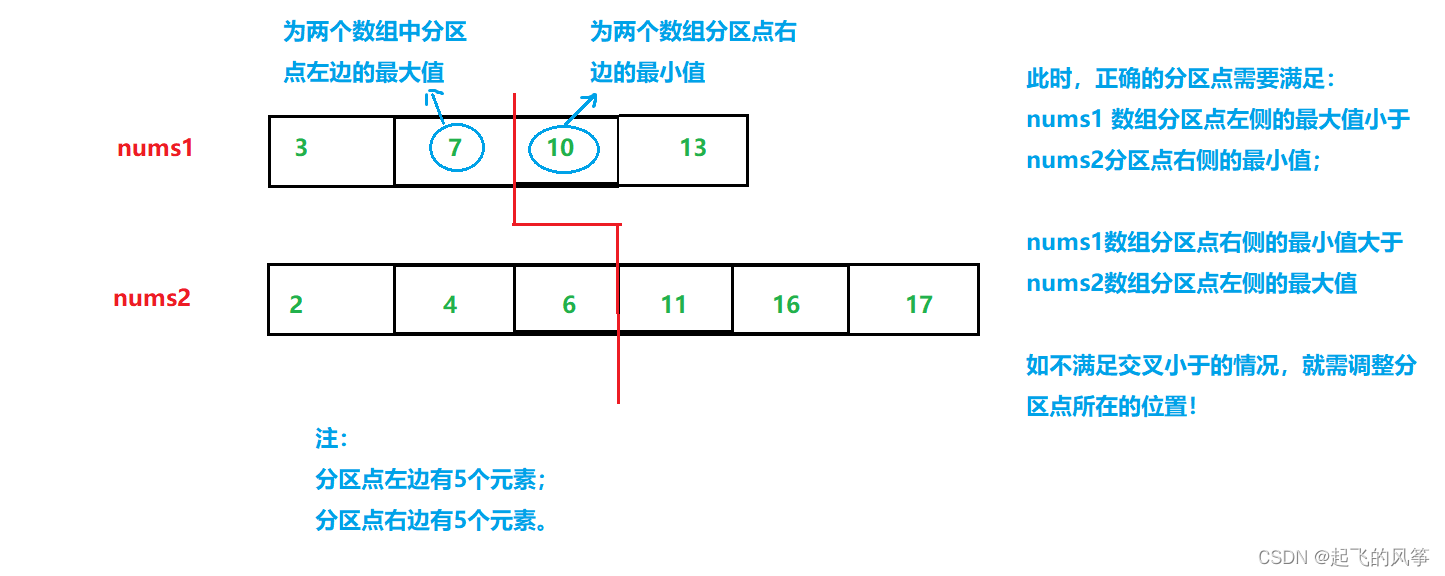
- 分区点不满足的示例:
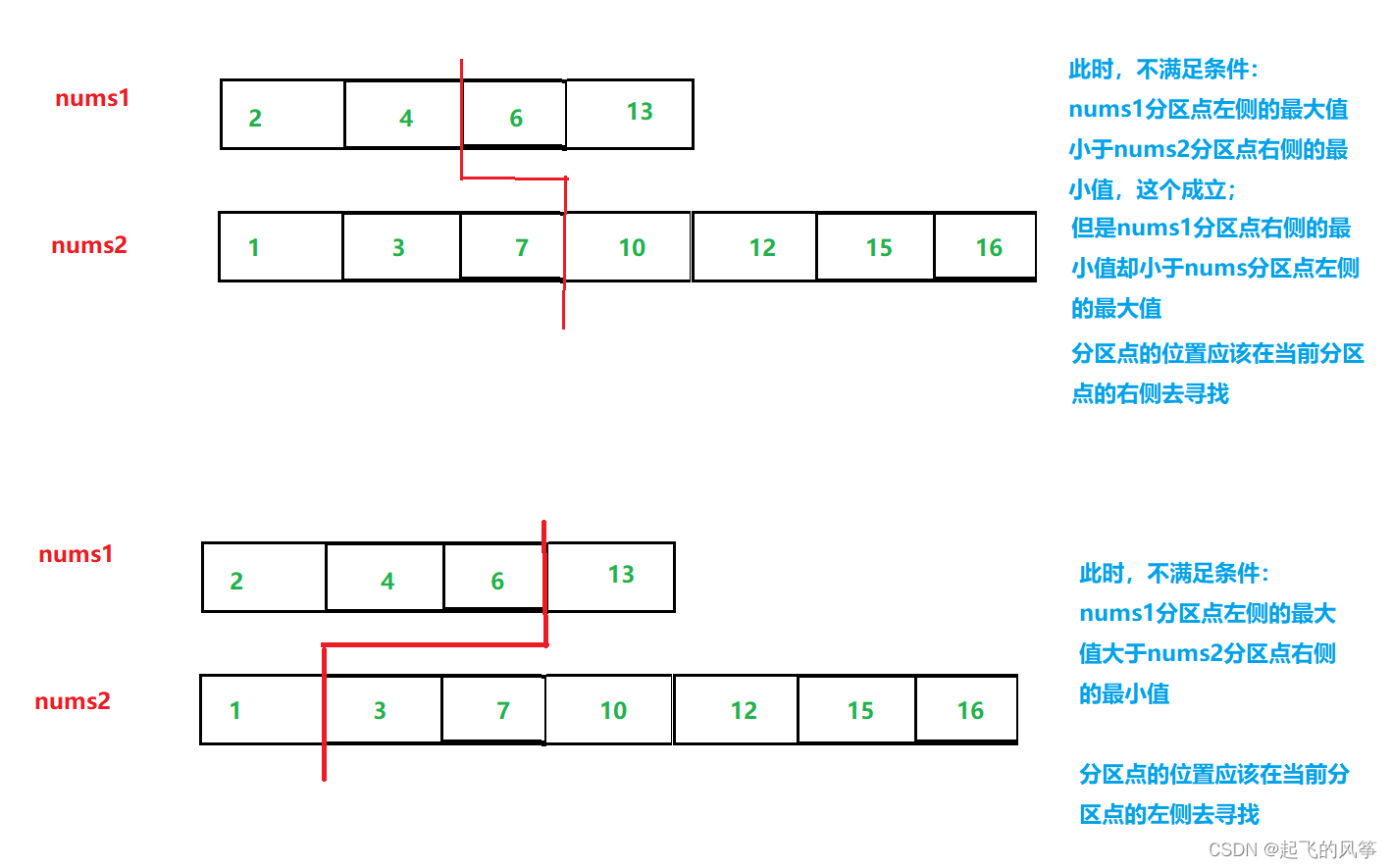
- 极端情况1:
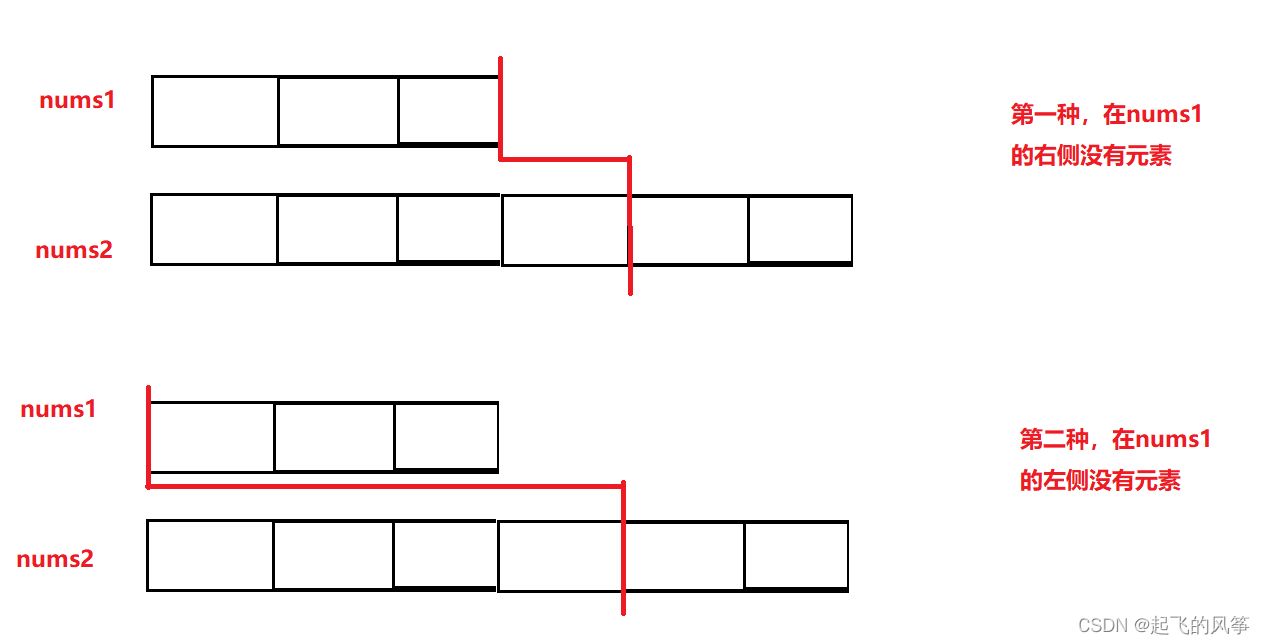
- 极端情况2:
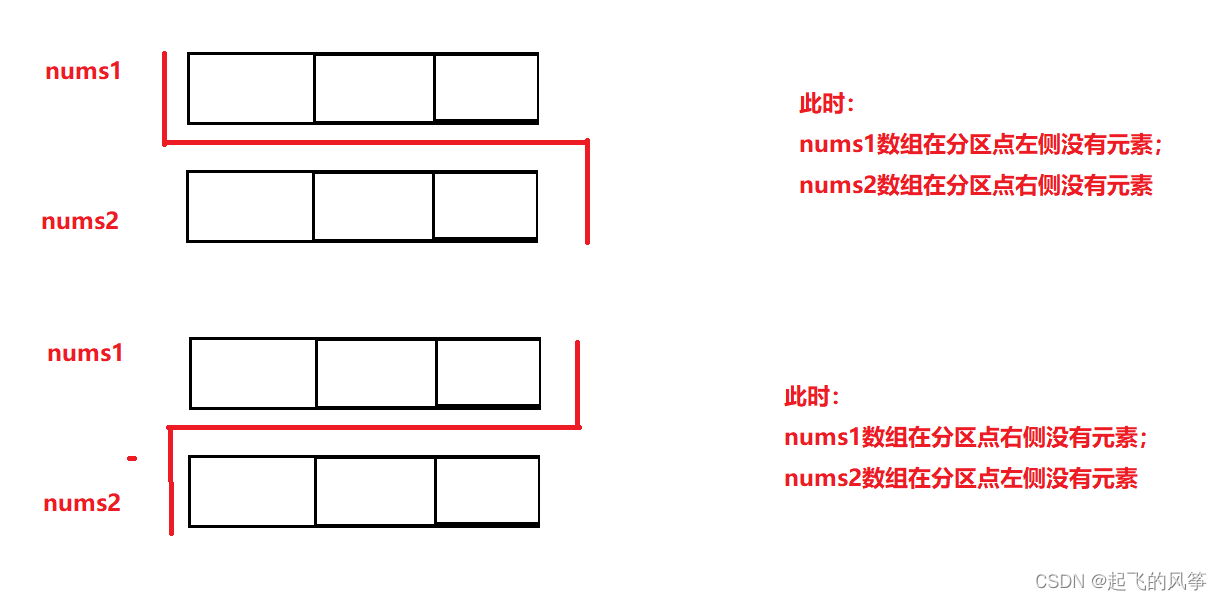
具体步骤:
- 首先,记录下两个数组的长度大小,以备后序的计算中位数做准备;
- 为了防止分区点的在第二个数组的两侧都有元素,导致出现数组越界的现象。在此实现中,我们首先检查第一个数组的长度是否大于第二个数组的长度。如果是,我们交换数组以确保第一个数组始终是较短的那个数组;
- 然后,我们使用二叉搜索来查找两个数组的分区点,我们计算分区点。使得两个数组中分区左侧的元素数小于分区右侧的元素数;
- 找到较短数组的分区点partition1,利用公式找到较长数组的分区点partition2;
- 然后我们检查分区点是否在数组的边界,如果没有,我们检查分区点处元素是否形成有效的中位数; 如果没有,我们可以相应的调整分区点;
- 如果分区点位于数组的边界或者分区点处的元素形成有效的中位数,我们可以计算两个数组的中位数;
- 然后,我们计算两个数组中分区左侧的最大元素和两个数组中分区右侧的最小元素,如果较短数组中分区左侧的最大元素小于或等于较长数组中分区右侧的最小元素 ,并且 较短数组中分区右侧的最小元素大于等于较长数组中分区左侧的最大元素 ,然后表明我们找到了中位数;
- 如果合并后数组的长度是偶数,我们取分区左侧最大元素和分区右侧最小元素的平均值;如果合并后数组的长度是奇数,我们取分区左侧最大元素作为作为中位数
代码如下:
class Solution {
public:double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {//记录两个数组的长度大小int m = nums1.size();int n = nums2.size();//确保第一个数组始终是较短数组if (m > n) {return findMedianSortedArrays(nums2, nums1);}//在较短数组的区间 【0,m】之间里查找出合适的分区点//使得较短数组满足我们需要的条件 int left = 0;int right = m;while (left <= right) {//找到较短数组的分区点partition1int partition1 = (left + right) / 2;//利用公式找到较长数组的分区点partition2int partition2 = (m + n + 1) / 2 - partition1;//然后我们检查分区点是否在数组的边界,如果没有,我们检查分区点处元素是否形成有效的中位数//如果没有,我们可以相应的调整分区点//较短数组找到分区点后,因为数组是已经排好序的//当 partition1=0 时,说明较小数组分割线左边没有值,为了不影响//nums1[partition1] <= nums2[partition2]和 Math.max(maxLeft1, maxLeft2)的判断//所以将它设置为int的最小值,即INT_MINint maxLeft1 = (partition1 == 0) ? INT_MIN : nums1[partition1 - 1];//较短数组找到分区点后,因为数组是已经排好序的//partition1 等于较小数组的长度时,说明较小数组分割线右边没有值,为了不影响// nums2[partition2] <= nums1[partition1] 和 Math.min(minRight1, minRight2)的判断,//所以将它设置为int的最大值,即INT_MAXint minRight1 = (partition1 == m) ? INT_MAX : nums1[partition1];//较长数组找到分区点后,因为数组是已经排好序的//当partition2等于0时,说明较长数组分割线左边没有值,为了不影响// nums2[partition2] <= nums1[partition1] 和 Math.max(maxLeft1, maxLeft2)的判断,//所以将它设置为int的最小值,即INT_MINint maxLeft2 = (partition2 == 0) ? INT_MIN : nums2[partition2 - 1];//较长数组找到分区点后,因为数组是已经排好序的//当partition2 == n,说明较长数组分割线右边没有值,为了不影响//nums1[partition1] <= nums2[partition2] 和 Math.min(minRight1, minRight2)的判断,//所以将它设置为int的最大值,即INT_MAXint minRight2 = (partition2 == n) ? INT_MAX : nums2[partition2];//然后,我们计算两个数组中分区左侧的最大元素和两个数组中分区右侧的最小元素//如果较短数组中分区左侧的最大元素小于或等于较长数组中分区右侧的最小元素 并且//较短数组中分区右侧的最小元素大于等于较长数组中分区左侧的最大元素 ,然后表明我们找到了中位数if (maxLeft1 <= minRight2 && maxLeft2 <= minRight1) {//如果合并后数组的长度是偶数,我们取分区左侧最大元素和分区右侧最小元素的平均值if ((m + n) % 2 == 0) {return (max(maxLeft1, maxLeft2) + min(minRight1, minRight2)) / 2.0;}//如果合并后数组的长度是奇数,我们取分区左侧最大元素作为作为中位数else {return max(maxLeft1, maxLeft2);}} //此处用了maxleft1 < minRight2的取反,当较小数组中分区点的左边的值大于较长数组中分区点的右边的值//表面右指针应该左移else if (maxLeft1 > minRight2) {right = partition1 - 1;} //满足条件,左指针继续右移到 partition1 + 1位置处else {left = partition1 + 1;}}return 0.0;}
};性能分析:
- 时间复杂度:O(logmin(m,n))),其中 m 和 n 分别是数组 nums1 和 nums2的长度。查找的区间是 [0,m],而该区间的长度在每次循环之后都会减少为原来的一半。所以,只需要执行 logm 次循环。由于每次循环中的操作次数是常数,所以时间复杂度为 O(logm)。由于我们可能需要交换 nums1 和 nums 2 使得 m≤n,因此时间复杂度是 O(logmin(m,n)))。
- 空间复杂度:因为不需要借助额外的空间,因此 空间复杂度为O(1)。
到此,本题便讲解结束了!!
相关文章:

《LeetCode 热题 HOT 100》——寻找两个正序数组的中位数
本期给大家带来的是是《LeetCode 热题 HOT 100》第四题——寻找两个正序数组的中位数的题目讲解!!!() 本文目录 💥题意分析 💥解题思路: 1、直接法 (❌) …...
Unity- 游戏结束以及重启游戏
文章目录游戏结束以及重启游戏建个游戏结束页面编写委托类 游戏主角 以及 ui管理类的脚本重启游戏游戏结束以及重启游戏 思路:利用Canvas创建好覆盖全屏的结束页面,默认关闭。游戏结束时,玩家控制的对象发起委托,ui管理收下委托&…...

NGK BeCu8·11铜合金板材
NGK BeCu811铜合金板材 CB498K、CuSn6Zn4Pb2-B、CC498K、CuSn6Zn4Pb2-C CB494K、CuSn5Pb9-B、CC494K、CuSn5Pb9-C CB495K、CuSn10Pb10-B、CC495K、CuSn10Pb10-C CB496K、CuSn7Pb15-B、CC496K、CuSn7Pb15-C CB497K、CuSn5Pb20-B、CC497K、CuSn5Pb20-C 日本古河连接器专用材料如:…...
电脑突然死机怎么办?正确做法在这!
案例:电脑突然死机怎么办? 【家人们,我刚刚正在做工作报告,突然间电脑就死机了,这可怎么办啊?有什么方法可以快速解决这个问题吗?急急急!】 电脑在使用过程中,有时会出…...
)
基于cell数组的MATLAB仿真(附上完整仿真源码)
MATLAB是一款强大的数学软件,它提供了许多数据结构来存储和处理数据。其中,cell数组是一种非常有用的数据结构,它允许在一个数组中存储不同类型的数据,包括数值、字符串、逻辑值和其他cell数组等。 文章目录简单代码完整仿真源码下…...

电脑蓝屏问题排查
最近电脑安装了最新win10,更新最新的驱动以后,开机几分钟后,会蓝屏重启,报错为: DRIVER_POWER_STATE_FAILURE 下载蓝屏分析工具BlueScreenView 问题出在ntoskrnl.exe bing搜索给出了二种解决方案: 1&a…...
SpringBoot配置slf4j + logback
文章目录日志体系结构在SpringBoot中使用slf4j logback日志框架四种常用的日志输出1. ConsoleAppender2. FileAppender3. RollingFileAppender之TimeBasedRollingPolicy4. RollingFileAppender之SizeAndTimeBasedRollingPolicy日志过滤1. 级别介绍2. 过滤节点filter介绍Spring…...

JAVA——网络编程基本概念
🎉🎉🎉点进来你就是我的人了 博主主页:🙈🙈🙈戳一戳,欢迎大佬指点!人生格言:当你的才华撑不起你的野心的时候,你就应该静下心来学习! 欢迎志同道合的朋友一起加油喔🦾&am…...

[JavaEE]----Spring02
文章目录Spring_day021,IOC/DI配置管理第三方bean1.1 案例:数据源对象管理1.1.1 环境准备1.1.2 思路分析1.1.3 实现Druid管理步骤1:导入druid的依赖步骤2:配置第三方bean步骤3:从IOC容器中获取对应的bean对象步骤4:运行程序1.1.4 实现C3P0管理步骤1:导入C3P0的依赖步…...
笔记本可自行更换CPU、独显了,老外用它手搓了台“PS5”
前面说到微软打算在 Win12 出来前搞出个模块化的Windows:下一个系统不是Win12,微软要复活Win10X。 模块化不用小蝾再过多介绍了,就像积木一样拼在一起组成一个整体。 优势就很明显了,由于每个部分都是单独的模块,更新…...

Linux uart驱动框架
Linux内核提供了标准的UART驱动程序,可以通过以下步骤编写: 首先需要定义一个结构体来存储串口设备数据。在该结构体中,包含一个uart_port结构体,用于与Linux内核通信,并包含一些设备特定的数据(例如波特率…...
第一个禁止ChatGPT的西方国家
意大利成为第一个有效禁止 ChatGPT 的西方国家。 由于可能违反隐私和数据法,该国的数据监管机构已下令开发聊天机器人的 OpenAI 停止运营。 意大利数据保护局 (GPDP) 提到了一些担忧,包括大量收集用户数据和存储以训练 AI 算法。 ChatGPT 是一种大型语…...
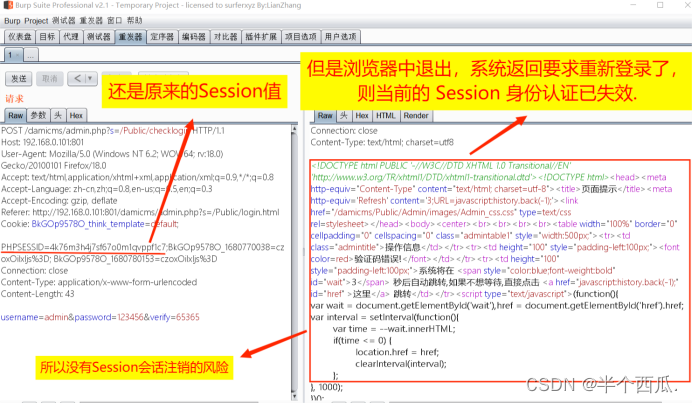
Web 攻防之业务安全:Session会话注销测试.
Web 攻防之业务安全:Session会话注销测试. 业务安全是指保护业务系统免受安全威胁的措施或手段。广义的业务安全应包括业务运行的软硬件平台(操作系统、数据库,中间件等)、业务系统自身(软件或设备)、业务所…...

4月最新编程排行出炉,第一名ChatGPT都在用~
作为一名合格的(准)程序员,必做的一件事是关注编程语言的热度,编程榜代表了编程语言的市场占比变化,它的变化更预示着未来的科技风向和机会! 快跟着一起看看本月排行有何看点: 4月Tiobe排行榜前…...

生成不保存在服务器的附件,并以附件形式发送邮件
需求:从数据库中抓取需要的数据,将数据生成excel表格,并将此表格以附件的形式放置到邮件中发送 //发送带附件的邮件,同时附件不会生成到服务器中public static String sendFileEmail(String form, String code, String to, String…...

Golang Gin框架HTTP上传文件
Golang Gin框架HTTP上传文件解析 文章目录Golang Gin框架HTTP上传文件解析HTTP上传的文件的原理Gin框架文件上传Demo限制文件上传的大小文件类型验证文件上传进度-后台计算文件上传进度HTTP上传的文件的原理 HTTP协议的文件上传是通过HTTP POST请求实现的,使用mult…...
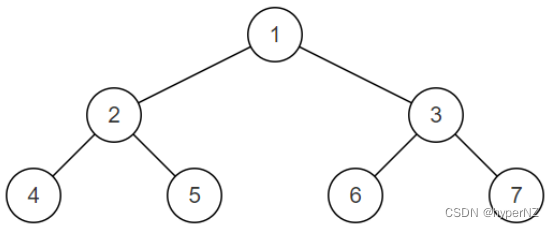
BM36-判断是不是平衡二叉树
题目 输入一棵节点数为 n 二叉树,判断该二叉树是否是平衡二叉树。 在这里,我们只需要考虑其平衡性,不需要考虑其是不是排序二叉树 平衡二叉树(Balanced Binary Tree),具有以下性质:它是一棵空…...

Quartz 单例定时任务
1、引入jar包,继承 Job 接口,编写需要执行的业务逻辑 <dependency><groupId>org.quartz-scheduler</groupId><artifactId>quartz</artifactId><version>2.3.2</version></dependency> public class D…...

不要告诉同事你要离职!打算跳槽,新公司开出两倍薪资,私下告诉要好的同事,却被同事出卖给领导!...
职场上有真正的朋友吗?来看看这位网友的讲述:一位前同事本来打算跳槽,新公司开出的薪资是原来的两倍。她私下告诉了几位同事自己打算离职的消息,并跟同事们分享了工资翻倍的喜悦。可她万万没想到,两天之后的公司会议上…...
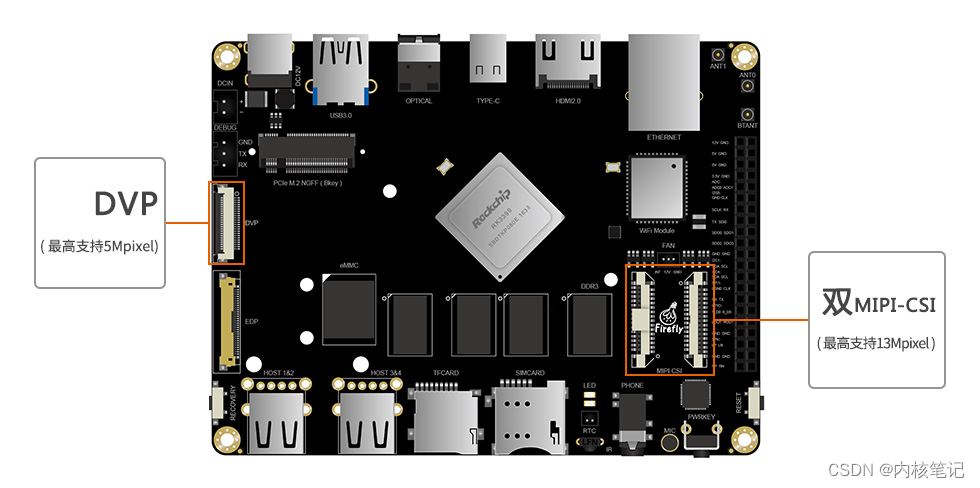
RK3399平台开发系列讲解(外设篇)Camera OV13850配置过程
🚀返回专栏总目录 文章目录 一、DTS 配置二、驱动说明三、配置原理四、cam_board.xml沉淀、分享、成长,让自己和他人都能有所收获!😄 📢我们以 OV13850/OV5640 摄像头为例,讲解在该开发板上的配置过程。 一、DTS 配置 isp0: isp@ff910000 {…status = "okay&quo…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

解决:Android studio 编译后报错\app\src\main\cpp\CMakeLists.txt‘ to exist
现象: android studio报错: [CXX1409] D:\GitLab\xxxxx\app.cxx\Debug\3f3w4y1i\arm64-v8a\android_gradle_build.json : expected buildFiles file ‘D:\GitLab\xxxxx\app\src\main\cpp\CMakeLists.txt’ to exist 解决: 不要动CMakeLists.…...

在 Spring Boot 中使用 JSP
jsp? 好多年没用了。重新整一下 还费了点时间,记录一下。 项目结构: pom: <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://ww…...

深度剖析 DeepSeek 开源模型部署与应用:策略、权衡与未来走向
在人工智能技术呈指数级发展的当下,大模型已然成为推动各行业变革的核心驱动力。DeepSeek 开源模型以其卓越的性能和灵活的开源特性,吸引了众多企业与开发者的目光。如何高效且合理地部署与运用 DeepSeek 模型,成为释放其巨大潜力的关键所在&…...

云安全与网络安全:核心区别与协同作用解析
在数字化转型的浪潮中,云安全与网络安全作为信息安全的两大支柱,常被混淆但本质不同。本文将从概念、责任分工、技术手段、威胁类型等维度深入解析两者的差异,并探讨它们的协同作用。 一、核心区别 定义与范围 网络安全:聚焦于保…...

Windows 下端口占用排查与释放全攻略
Windows 下端口占用排查与释放全攻略 在开发和运维过程中,经常会遇到端口被占用的问题(如 8080、3306 等常用端口)。本文将详细介绍如何通过命令行和图形化界面快速定位并释放被占用的端口,帮助你高效解决此类问题。 一、准…...
