C#,初学琼林(06)——组合数的算法、数据溢出问题的解决方法及相关C#源代码
1 排列permutation
排列,一般地,从n个不同元素中取出m(m≤n)个元素,按照一定的顺序排成一列,叫做从n个元素中取出m个元素的一个排列(permutation)。特别地,当m=n时,这个排列被称作全排列(all permutation)。
注:当且仅当两个排列的元素完全相同,且元素的排列顺序也相同,则两个排列相同。例如,abc与abd的元素不完全相同,它们是不同的排列;又如abc与acb,虽然元素完全相同,但元素的排列顺序不同,它们也是不同的排列
排列可分选排列与全排列两种,在从n个不同元素取出m个不同元素的排列种,当m<n时,这个排列称为选排列;当m=n时,这个排列称为全排列。
重复排列(permutationwith repetiton)是一种特殊的排列。从n个不同元素中可重复地选取m个元素。按照一定的顺序排成一列,称作从n个元素中取m个元素的可重复排列。当且仅当所取的元素相同,且元素的排列顺序也相同,则两个排列相同。
2 组合 combination
组合(combination)是一个数学名词。一般地,从n个不同的元素中,任取m(m≤n)个元素为一组,叫作从n个不同元素中取出m个元素的一个组合。我们把有关求组合的个数的问题叫作组合问题。
组合总数(total number of combinations)是一个正整数,指从n个不同元素里每次取出0个,1个,2个,…,n个不同元素的所有组合数的总和。
重复组合(combination with repetiton)是一种特殊的组合。从n个不同元素中可重复地选取m个元素。不管其顺序合成一组,称为从n个元素中取m个元素的可重复组合。当且仅当所取的元素相同,且同一元素所取的次数相同,则两个重复组合相同。
3 组合数(组合总数)的计算方法C#源代码
using System;namespace Legalsoft.Truffer
{public static partial class XMath{/// <summary>/// 计算组合数C(M,N) M>=N/// </summary>/// <param name="M"></param>/// <param name="N"></param>/// <returns></returns>public static int Combine(int M, int N){ulong ret = 1L;for (int i = M - N + 1; i <= M; i++){ret *= (ulong)i;}for (int i = 2; i <= N; i++){ret /= (ulong)i;}return (int)ret;}}
}4 计算组合数的数据溢出问题
上述的代码,计算 C(12,5) 是没有问题的。但是,如果计算 C(100,50)!
结果 = 0 !!!
这是因为太多的数相乘,超过了 ulong 允许的最大数,这就是数据超界的问题。
5 组合总数递归算法的C#源程序
namespace Legalsoft.Truffer
{public static partial class XMath{/// <summary>/// 计算组合数C(M,N) M>=N/// </summary>/// <param name="M"></param>/// <param name="N"></param>/// <returns></returns>public static int Combine_Recursion(int M, int N){if (M < N) return 0;if (M <= 0 || N <= 0) return 1;return Combine_Recursion(M - 1, N) + Combine_Recursion(M - 1, N - 1);}}
}递归算法可解决数值溢出问题,但会带来堆栈溢出问题,可谓“按下葫芦浮起瓢”。
6 计算组合数的追溯法(BackTrack,亦称回溯法)C#源代码
using System;namespace Legalsoft.Truffer
{public static partial class XMath{private static int num = 0;private static ulong bestnum = 0L;/// <summary>/// 追溯法计算组合数/// </summary>/// <param name="M"></param>/// <param name="N"></param>/// <returns></returns>public static ulong Combine_Backtrack(int M, int N){num = 0;bestnum = 0L;BackTrack(1, M, N);return bestnum;}/// <summary>/// 内部递归函数/// </summary>/// <param name="k"></param>/// <param name="n"></param>/// <param name="m"></param>private static void BackTrack(int k, int n, int m){if (k > n){if (num == m){bestnum++;}}else{for (int i = 0; i <= 1; i++){if (i == 0){BackTrack(k + 1, n, m);}else{if (num <= m){num = num + 1;BackTrack(k + 1, n, m);num = num - 1;}}}}}}
}
世界上没有十全十美的人,也没有十全十美的事!
回溯算法同样存在大问题,而且是致命问题:
(1)计算效率太低,速度太慢!
(2)另外会导致堆栈溢出问题。
大数的组合 有其他计算方法,以后再介绍。
本文暂且做个了解。
相关文章:

C#,初学琼林(06)——组合数的算法、数据溢出问题的解决方法及相关C#源代码
1 排列permutation 排列,一般地,从n个不同元素中取出m(m≤n)个元素,按照一定的顺序排成一列,叫做从n个元素中取出m个元素的一个排列(permutation)。特别地,当mn时,这个排列被称作全…...

MySQL数据库——绘制E-R图:数据库概要设计阶段
在MySQL数据库的概要设计阶段,绘制E-R图是非常重要的一步。E-R图(实体关系图)是一种图形化的工具,用于描述数据库中实体之间的关系。 以下是在MySQL数据库概要设计阶段绘制E-R图的步骤: 确定实体:在MySQL数…...

对类和对象的理解
对象:对象是人们要进行研究的任何事物,它不仅能表示具体的事物,还能表示抽象的规则、计划或事件。对象具有状态,一个对象用数据值来描述它的状态。对象还有操作,用于改变对象的状态,对象及其操作就是对象的…...

edge-tts微软文本转语音库,来听听这些语音是否很熟悉?
上期图文教程,我们分享了Azure机器学习的文本转语音的账号申请与API申请的详细步骤,也介绍了基于python3实现Azure机器学习文本转语音功能的代码实现过程,虽然我们可以使用Azure账号免费提供一年的试用期,但是毕竟是要付费的,我们的API也无法长期使用,好在微软发布了edge…...

MySQL更换存储引擎
要更换 MySQL 5.7 中某个表的存储引擎,可以使用以下的 SQL 命令: sql复制代码 ALTER TABLE table_name ENGINEengine_name; 其中,table_name 是需要更换存储引擎的数据表名称,engine_name 则是需要更换成的新存储引擎名称。 举…...

filebeat收集不规则多行日志
现环境有多行日志输出内容和格式不确定,合并后使用grok默认正则无法收集,需要自己编写正则 日志内容如下: ERROR|2023-04-06 14:27:52|helper|test|http|/api/ad/listBanner|1d60fff861bqwe4b0397be554141eb 127.0.0.1|1b4429-5adb-44d4-acf…...
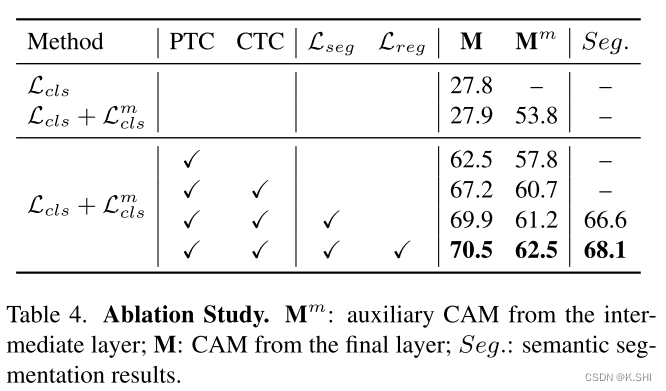
Token Contrast for Weakly-Supervised Semantic Segmentation
文章来源:[CVPR2023] Keywords:Weakly-Supervised Semantic Segmentation(WSSS);over-smoothing; ViT 一、本文提出的问题以及解决方案: 本文解决了over-smoothing问题,该问题其实是在之前的GCN网络中提出…...

Jenkins运行在docker中使用Maven构建Java应用程序
这篇笔记是Jenkins入门教程使用Maven构建Java应用程序的一个补充说明,因为我照着文档操作的过程中遇到不少问题,遂一一做个笔记。 我的主机是Windows 11,安装的docker是Docker Desktop 4.18.0。 第一点,在Windows里执行docker命…...
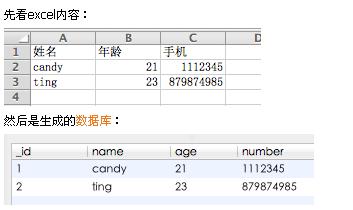
将excel导入到sqlite的方法代码
Python实现excel转sqlite的方法,具体如下: Python环境的安装配置就不说了,个人喜欢pydev的开发环境。 python解析excel需要使用第三方的库,这里选择使用xlrd 下面是源代码: #!/usr/bin/python # encodingutf-8 Creat…...

Redis主从复制、哨兵和集群部署
文章目录一、主从复制1、主从复制-哨兵-集群2、主从复制的概念3、主从复制的作用4、主从复制流程5、部署Redis 主从复制步骤6、实例操作:部署Redis 主从复制二、哨兵模式1、哨兵模式的原理2、哨兵模式的作用3、哨兵结构由两部分组成,哨兵节点和数据节点4…...

protobuf序列化
文章目录protubufprotobuf序列化protobuf的原理定义message编译message文件应用protobufMessage 基本用法Message 嵌套使用protubuf protobuf序列化 protobuf是一种比json和xml等序列化工具更加轻量和高效的结构化数据存储格式,性能比json和xml真的强很多ÿ…...
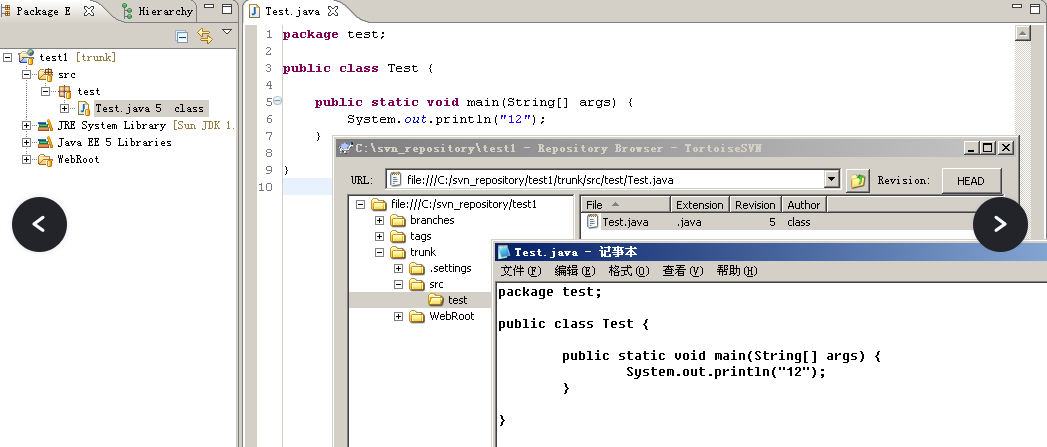
更新时无冲突的情况(阁瑞钛伦特软件-九耶实训)
大多数使用“与资源库同步”菜单的目的是想查看本地和远程资源的差异,并不想将本地的内容进行更新。 而“更新”菜单则不然,它的主要作用是将远程仓库中的内容下载到本地,以使本地的版本内容和仓库中的内容一致。 Step01:复用前…...

3.4 函数的单调性和曲线的凹凸性
学习目标: 如果我要学习函数的单调性和曲线的凹凸性,我会采取以下几个步骤: 理解概念和定义:首先,我会学习单调性和凹凸性的定义和概念。单调性是指函数的增减性质,可以分为单调递增和单调递减;…...

LeetCode 404. 左叶子之和 | C++语言版
LeetCode 404. 左叶子之和 | C语言版LeetCode 404. 左叶子之和题目描述解题思路思路一:使用递归代码实现运行结果参考文章:思路二:减少遍历节点数代码实现运行结果参考文章:LeetCode 404. 左叶子之和 题目描述 题目地址…...

arm架构安装Rancher并导入k8s集群解决Error: no objects passed to apply
Rancher介绍 Rancher 2.0-2.4版本 是一个开源的企业级容器管理平台。通过Rancher,企业再也不必自己使用一系列的开源软件去从头搭建容器服务平台。Rancher提供了在生产环境中使用的管理Docker和Kubernetes的全栈化容器部署与管理平台。 Rancher 2.5版本 是为使用容…...
安装PaddleSpeech
github地址https://github.com/PaddlePaddle/PaddleSpeech 创建虚拟环境 conda create -p E:\Python\envs\nlppaddle python3.7 # conda create -p E:\Python\envs\speechstu python3.8激活虚拟环境 conda activate E:\Python\envs\nlppaddle # conda activate E:\Python\…...
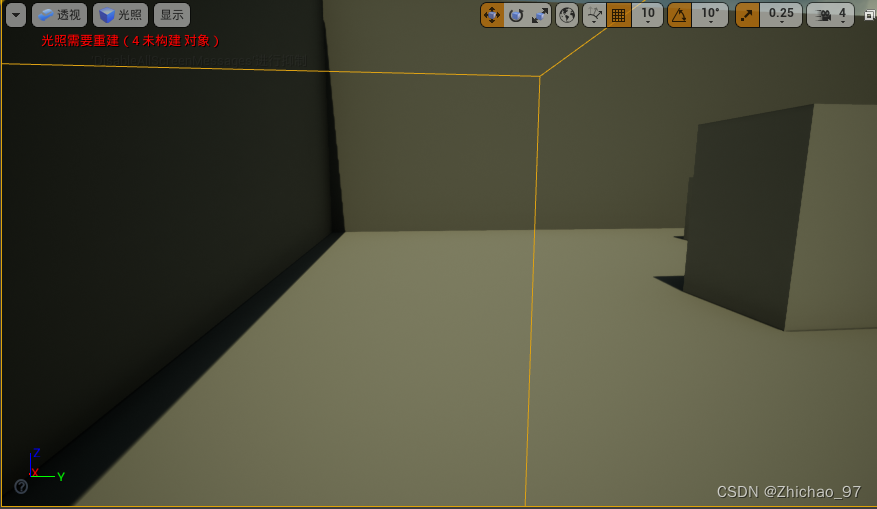
UE “体积”的简单介绍
目录 一、阻挡体积 二、摄像机阻挡体积 三、销毁Z体积 四、后期处理体积 一、阻挡体积 你可以在静态网格体上使用阻挡体积替代碰撞表面,比如建筑物墙壁。这可以增强场景的可预测性,因为物理对象不会与地面和墙壁上的凸起细节相互作用。它还能降低物理模…...

微信 JAVA SDK 封装
weixin-popular 微信 JAVA SDK,是微信平台(公众平台、开放平台、商户平台、服务商平台)接口服务的JAVA 实现,开发 严格按照官方技术文档,合理划分包名、定义字段及方法,能胜任任何微信相关的业务。 使用建…...

上海智慧校园视频智能分析算法 yolov7
上海智慧校园视频智能分析算法通过yolov7python网络模型分析技术,上海智慧校园视频智能分析算法对校园内学生打架、翻墙、倒地、异常聚集、攀高等行为实时监测预警。YOLOv7 的发展方向与当前主流的实时目标检测器不同,研究团队希望它能够同时支持移动 GP…...
【树】你真的会二叉树了嘛? --二叉树LeetCode专题
Halo,这里是Ppeua。平时主要更新C语言,C,数据结构算法......感兴趣就关注我吧!你定不会失望。 🌈个人主页:主页链接 🌈算法专栏:专栏链接 我会一直往里填充内容哒! &…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...
