【数据结构】算法的复杂度分析:让你拥有未卜先知的能力

- 👑专栏内容:数据结构
- ⛪个人主页:子夜的星的主页
- 💕座右铭:日拱一卒,功不唐捐
文章目录
- 一、前言
- 二、时间复杂度
- 1、定义
- 2、大O的渐进表示法
- 3、常见的时间复杂度
- 三、空间复杂度
- 1、定义
- 2、常见的空间复杂度
一、前言
一个程序能用很多不同的算法来实现,那么到底那种算法是效率最高的呢?
对此我们有两种方法:
第一种是事后统计法,既在编写之后,通过计时,比较不同算法编写的程序的运行时间,以此确定算法效率的高低。但是该方法的缺陷很大,会受到测试环境、数据规模的影响。
第二种是事前分析法,即在编写之前,依据一些统计方法对算法进行粗略估算,大致的估算出该算法的时间复杂度和空间复杂度,通过对比复杂度来评判那种算法的效率更高。

可以说,学会了如何分析一个算法的复杂度,就拥有了未卜先知的能力,即在这个算法被写出来之前,就能大致评判出这个算法的好坏。
二、时间复杂度
1、定义
维基百科:在计算机科学中,算法的时间复杂度(time complexity)是一个函数,它定性描述该算法的运行时间。这是一个代表算法输入值的字符串的长度的函数。时间复杂度常用大O符号表述,不包括这个函数的低阶项和首项系数。使用这种方式时,时间复杂度可被称为是渐近的,亦即考察输入值大小趋近无穷时的情况。

额…具体来举个例子吧。
void Func1(int N)
{
int count = 0;
// n*n次
for (int i = 0; i < N ; ++ i)
{for (int j = 0; j < N ; ++ j){++count;}
}
// 2*n次
for (int k = 0; k < 2 * N ; ++ k)
{++count;
}
// 10次
int M = 10;
while (M--)
{++count;
}
printf("%d\n", count);
}
这个函数一共执行的基本操作次数为:F(n)=n2+2∗n+10F(n)=n^2+2*n+10F(n)=n2+2∗n+10
但是,我们计算复杂度的时候,不一定需要计算这么精确的执行次数,我们只需要计算出大概的执行次数就行了,所以这里我们应该使用大O的渐进表示法。那么什么是大O表示法呢?
2、大O的渐进表示法
大O符号(Big O notation):是用于描述函数渐进行为(趋向于特定值或无穷大)的数学符号。
上面函数一共执行的操作次数为:F(n)=n2+2∗n+10F(n)=n^2+2*n+10F(n)=n2+2∗n+10
学过极限的都知道,当nnn趋向于无穷的时候,n2+2∗n+10n^2+2*n+10n2+2∗n+10 中的2∗n2*n2∗n和10可以忽略不记。
所以用大O的渐进表示法,上面函数的时间复杂度应该为:O(n2)O(n^2)O(n2)
这里我们可以简单的总结一下方法:
1、用常数1取代运行时间中的所有加法常数。
2、在修改后的运行次数函数中,只保留最高阶项。
3、嵌套代码的复杂度等于嵌套内外代码复杂度的乘积。
4、如果最高阶项存在且不是1,则去除与这个项目相乘的常数。
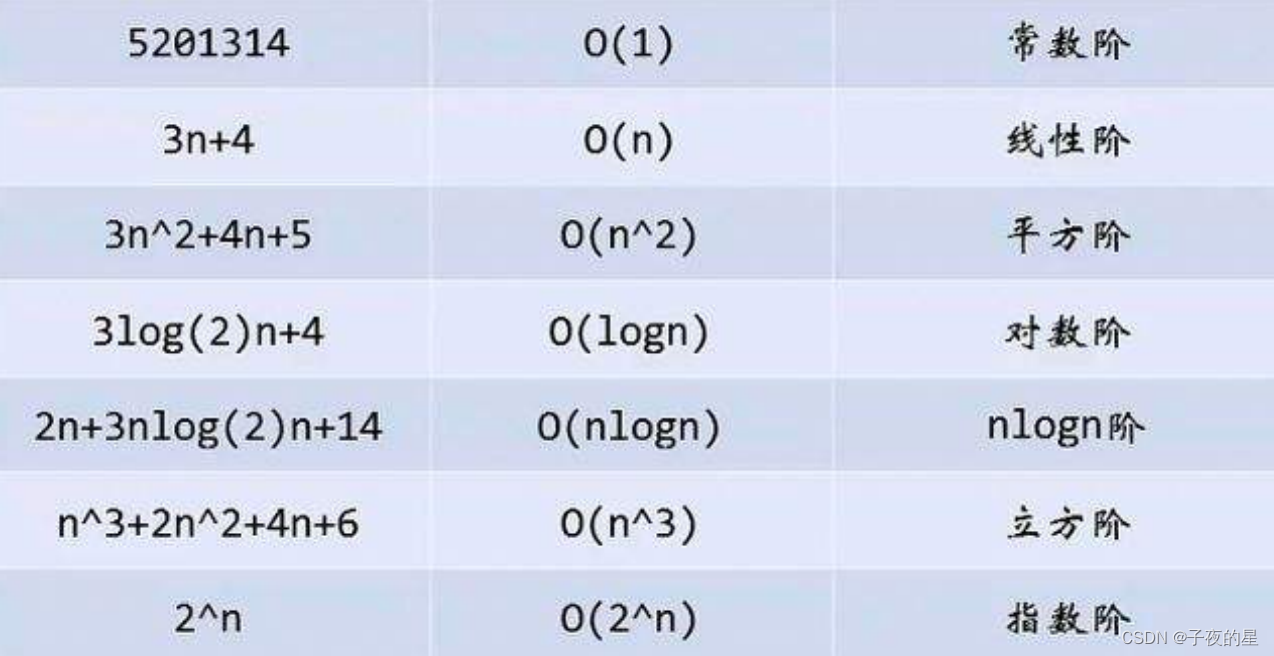
3、常见的时间复杂度
- O(1)O(1)O(1)型
一般情况下,要算法的执行时间不随问题规模 n 的增加而增大,那么就是O(1)O(1)O(1)的时间复杂度
void Func(int n)
{int count = 0;for (int k = 0; k < 100; ++ k){++count;}printf("%d\n", count);
}
以上代码看似存在循环,但是仔细看,当循环到第十次的时候,这个循环就停止了。
所以上面的时间复杂度为 O(1)O(1)O(1)
- O(logn)O(logn)O(logn)型
类似于二分查找、幂运算都是O(logn)O(logn)O(logn)的时间复杂度
void Func(int n)
{int i=1;while (i <= n) {i = i * 2;}
}
以上代码,变量 i 从 1 开始,每循环一次就乘以 2。当大于n时,循环结束。所以,假设一共循环了xxx次,那么我们就可以得到:2x=n2^x=n2x=n 即x=log2nx=log_2nx=log2n ,忽略掉底数2,则该时间复杂度为:O(logn)O(logn)O(logn)

为什么可以忽略掉底数?
高中学过的换底公式:logbn=logba∗loganlog_bn=log_ba*log_anlogbn=logba∗logan
现在假设底数不是2是3,我们可以把log3nlog_3nlog3n写成log32∗log2nlog_32*log_2nlog32∗log2n,根据前面的规矩:如果最高阶项存在且不是1,则去除与这个项目相乘的常数。 而这里的log32log_32log32是个常数,可以直接去除。所以兜兜转转,最后的时间复杂度还是O(logn)O(logn)O(logn)
- O(nlogn)O(nlogn)O(nlogn)型
void Func(int n)
{for (int i = 1; i <= n; i++){int j = 1;while (j <= n){j = j * 2;}}
}
根据上面可以知道,这个循环里面的循环的复杂度是O(logn)O(logn)O(logn),而这个循环又要执行n次,所以算下来,它的时间复杂度是O(nlogn)O(nlogn)O(nlogn)
- O(n)O(n)O(n)型
void Func(int n)
{for (int i = 1; i <= n; i++){printf("我一共执行了n次哦!");}
}
- O(n2)O(n^2)O(n2)型
循环套循环,每个循环都是n次
void Func(int n)
{for (int i = 1; i <= n; i++){for (int j = 1; j <= n; j++){printf("我一共执行了n*n次哦!");}}
}
- O(m∗n)O(m*n)O(m∗n)型
void Func(int n,int m)
{for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++){printf("看的出来我有那些不一样吗?");}}
}

确实还有其他很多不同的时间复杂度,比如,O(2n)、O(n!)O(2^n)、O(n!)O(2n)、O(n!)…但是这些时间复杂度都太高了,以至于高到很多计算机都承受不了,所以比较少见。

三、空间复杂度
1、定义
维基百科:在计算机科学中,一个算法或程序的空间复杂度定性地描述该算法或程序运行所需要的存储空间大小。空间复杂度是相应计算问题的输入值的长度的函数,它表示一个算法完全执行所需要的存储空间大小。和时间复杂度类似,空间复杂度通常也使用大O记号来渐进地表示例如O(n)、O(nlogn)O(n)、O(nlogn)O(n)、O(nlogn)其中n用来表示输入的长度,该值可以影响算法的空间复杂度。
就像时间复杂度的计算不考虑算法所使用的空间大小一样,空间复杂度也不考虑算法运行需要的时间长短。
注意:函数运行时所需要的栈空间(存储参数、局部变量、一些寄存器信息等)在编译期间已经确定好了,因此空间复杂度主要通过函数在运行时候显式申请的额外空间来确定。
2、常见的空间复杂度
- O(1)型O(1)型O(1)型
无论 n 的值如何变化,代码在执行过程中开辟的内存空间是固定的
void Func(int n)
{int i = 0; int sum = 0;for (i = 1; i < n; i++){sum = sum + i;}
}
这段代码之开辟了sum和i两个int类型的空间,大小是固定的。
所以这段代码的空间复杂度为O(1)O(1)O(1)
- O(n)型O(n)型O(n)型
随着n的值的增大,开辟的空间也逐渐增大
long long Fac(size_t N)
{if(N == 0)return 1;return Fac(N-1)*N;
}
这段代码递归调用了N次,开辟了N个栈帧,每个栈帧使用了常数个空间。
所以这段代码的空间复杂度为O(N)O(N)O(N)
- O(n2)型O(n^2)型O(n2)型
int** fun(int n) {int ** s = (int **)malloc(n * sizeof(int *));while(n--)s[n] = (int *)malloc(n * sizeof(int));return s;}
此处开辟的是一个二维数组,数组有n行,每行分别有1,2,3,…n列,所以是n(n+1)/2n(n + 1)/2n(n+1)/2个元素空间,空间复杂度为n2n^2n2

相关文章:

【数据结构】算法的复杂度分析:让你拥有未卜先知的能力
👑专栏内容:数据结构⛪个人主页:子夜的星的主页💕座右铭:日拱一卒,功不唐捐 文章目录一、前言二、时间复杂度1、定义2、大O的渐进表示法3、常见的时间复杂度三、空间复杂度1、定义2、常见的空间复杂度一、前…...
Linux根文件系统移植
目录 一、根文件系统 1.1根文件系统 1.2根文件系统内容 二、根文件系统移植 2.1BusyBox 2.2BusyBox的获取 2.3BusyBox的使用 2.4make menuconfig 2.5编译和安装 2.6修改根文件系统 一、根文件系统 1.1根文件系统 根文件系统是内核启动后挂载的第一个文件系统系统引…...
Three.js 无限平面快速教程【Plane】
Three.js 提供了 Plane 概念来表示在 3d 空间中无限延伸的二维表面。 这对于光标交互很有用,因此你可能需要了解如何设置此平面、将其可视化并根据需要进行调整。 推荐:使用 NSDT场景设计器 快速搭建 3D场景。 Three.js 的 Plane 文档很好而且准确&…...
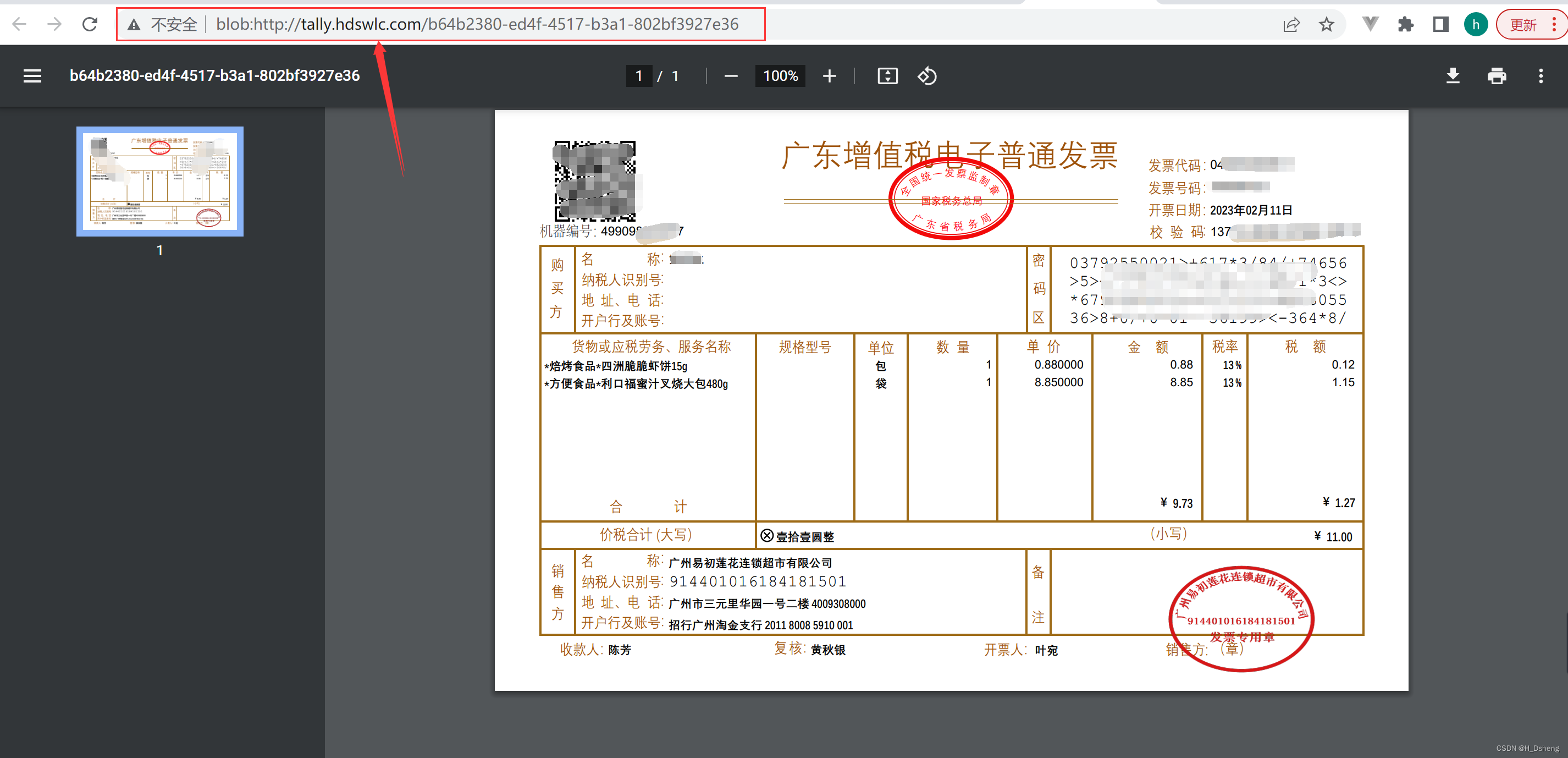
在线预览PDF文件、图片,并且预览地址不显示文件或图片的真实路径。
实现在线预览PDF文件、图片,并且预览地址不显示文件或图片的真实路径。1、vue使用blob流在线预览PDF、图片(包括jpg、png等格式)。1、按钮的方法:2、方法详细:(此方法可以在发起请求时携带token,…...
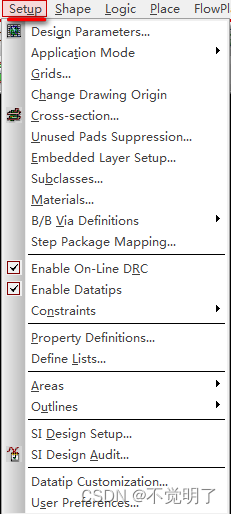
Allegro如何设置导入Subdrawing可自由选择目录操作指导
Allegro如何设置导入Subdrawing可自由选择目录操作指导 用Allgro做PCB设计的时候,导入Subdrawing是非常常用的功能,在导入Subdrawing的时候,通常需要把Subdrawing文件放在需要导入PCB的相同目录下,不能自由选择,如下图 但是Allegro是支持自由选择目录的,只需按照下方的步…...

SpirngMVC执行原理--自学版
DispatcherServlet表示前置控制器,是整个SpringMVC的控制中心,用户发出请求,DispatcherServlet接收请求并拦截请求HandlerMapper为处理器映射。DispatcherServlet调用。HandlerMapping根据请求url查找HandlerHandlerExecution表示具体的Handl…...

获取savemodel的输入输出节点
saved_model_cli show --dir savemodels --all 结果: MetaGraphDef with tag-set: ‘serve’ contains the following SignatureDefs: signature_def[‘translation_signature’]: The given SavedModel SignatureDef contains the following input(s): inputs[‘i…...
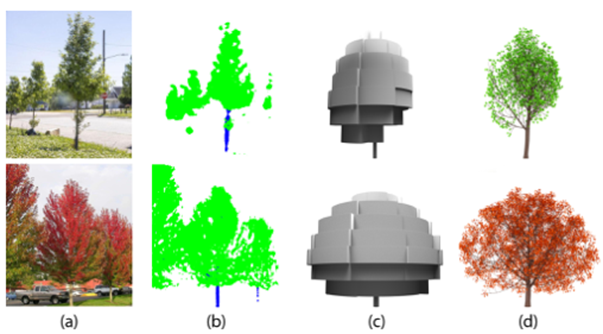
《Learning to Reconstruct Botanical Trees from Single Images》学习从单幅图像重建植物树
读书报告下载https://download.csdn.net/download/weixin_43042683/87448211论文原文https://dl.acm.org/doi/10.1145/3478513.3480525论文视频https://www.bilibili.com/video/BV1cb4y127Vp/?fromseopage&vd_source5212838c127b01db69dcc8b2d27ca5171引言植物存在在室外与…...

vant 4 正式发布,支持暗黑主题,那么是如何实现的呢
2022年10月25日首发于掘金,现在同步到公众号。11. 前言大家好,我是若川。我倾力持续组织了一年多源码共读,感兴趣的可以加我微信 lxchuan12 参与。另外,想学源码,极力推荐关注我写的专栏《学习源码整体架构系列》&…...

MySQL的复制 二
复制是MySQL的一项功能,使服务器能够将更改从一个实例恢复到另一个实例 主服务器(master)将所有数据和结构更改记录到二进制日志中。二进制日志格式是基于语句的、基于行的和混合的。 从属服务器(slave)从主服务器请求…...
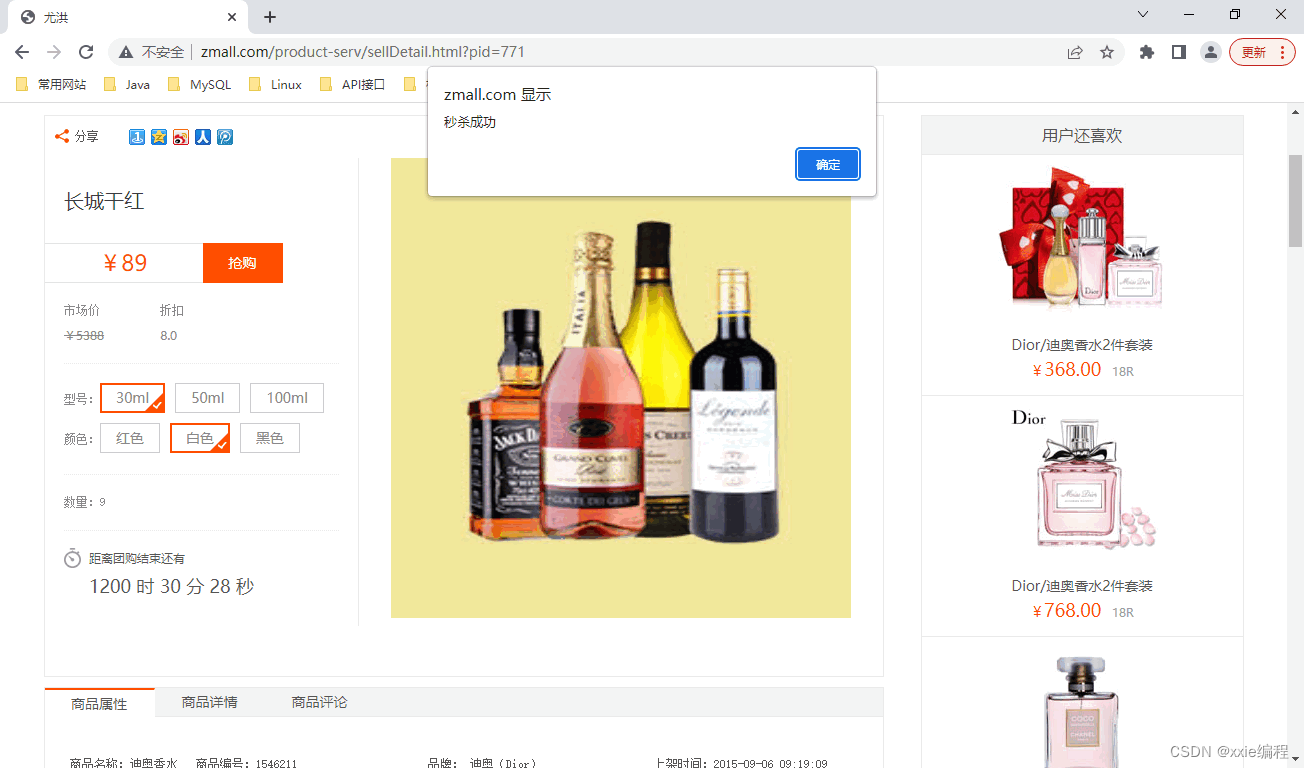
秒杀项目之秒杀商品展示及商品秒杀
目录前言一、登录方式调整二、生成秒杀订单2.1 绑定秒杀商品2.2 查看秒杀商品2.3 订单秒杀2.3.1 移除seata相关(方便测压)2.3.2 生成秒杀订单2.3.3 前端页面秒杀测试注意前言 博主博客用到的资源都会同步分享到资源包中 一、登录方式调整 第1步…...

教育行业需要什么样的数字产品?
数字化转型的浪潮已经席卷了各行各业,不仅出现在互联网、电商、建筑等行业,还应用在了教育行业。数字化的教育ERP软件能够在满足学校需求的基础上,帮助学校完善各类工作流程,提高工作效率。 对于一个拥有多个校区,上万…...
Spring MVC
一、Spring MVC介绍 a. Spring MVC是一个Web框架 b. Spring MVC是基于Servlet API构成的 MVC 是 Model View Controller 的缩写。 MVC 是⼀种思想,⽽ Spring MVC 是对 MVC 思想的具体实现。 学习Spring MVC目标: a.连接功能:将用户ÿ…...

类与对象(上)
类与对象(上) 1.面向过程和面向对象初步认识 C语言是面向过程的,关注的是过程,分析出求解问题的步骤,通过函数调用逐步解决问题。 C是基于面向对象的,关注的是对象,将一件事情拆分成不同的对象,靠对象之间…...

正确安装 torch_geometric库
step1: 查看pytorchcuda 版本 torch-scatter torch-sparse torch-cluster torch-spline-conv 这些关联包要与torch版本匹配。 import torch print(torch.__version__) print(torch.cuda.is_available()) torch.version.cuda或者 pip list查看版本 step2ÿ…...
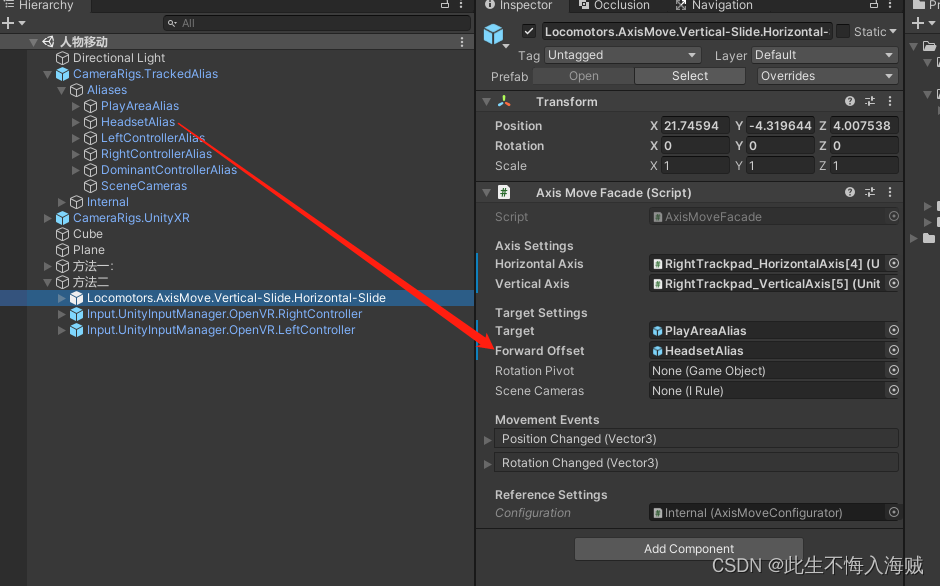
【Unity VR开发】结合VRTK4.0:自身移动(滑动)
语录: 依山傍水房树间,行也安然,住也安然; 一条耕牛半顷田,收也凭天,荒也凭天; 雨过天晴驾小船,鱼在一边,酒在一边; 夜晚妻子话灯前,今也谈谈…...
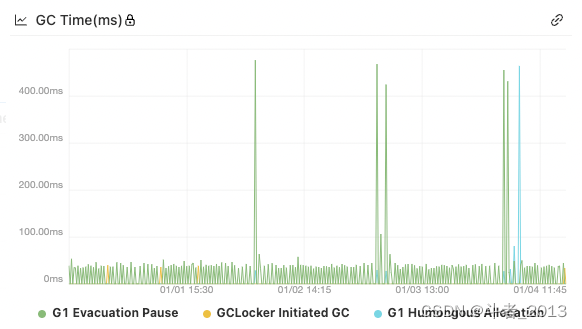
G1垃圾回收器详解
文章目录前言一、思考问题二、官方文档三、基本介绍四、G1的内存模型五、G1的标记过程六、G1的垃圾回收1、G1过程梳理2、Young GC3、Mixed GC4、Full GC七、参数介绍八、典型问题1、疏散失败(Evacuation Failure)2、大对象分配(Humongous All…...

tws耳机哪个牌子音质好?tws耳机音质排行榜
随着蓝牙耳机市场的不断发展,使用蓝牙耳机的人也逐渐增多,近年来更是超越有线耳机成为最火爆的数码产品之一。那么,tws耳机哪个牌子音质好?下面,我来给大家推荐几款音质好的tws耳机,可以当个参考。 一、南…...

TIA博途中DB数据块清零的具体方法示例
TIA博途中DB数据块清零的具体方法示例 TIA中数据块如何实现清零? 在TIA指令集内有多个移动指令可对DB块内数据进行清零处理。对于S7-1500 CPU或ET200SP CPU来说,可使用BLKMOV、FILL以及SCL的POKE_BLK指令。但是这些指令对DB块清零时,要求DB块必需为非优化DB。 对于优化的DB…...
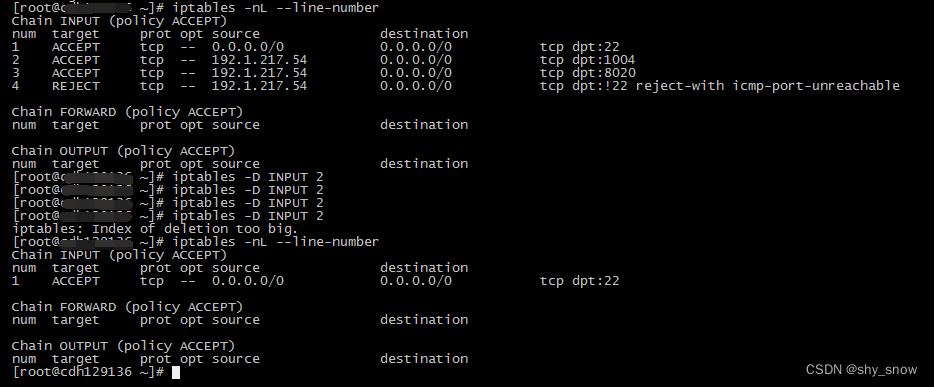
iptables防火墙屏蔽指定ip的端口
因为需要测试客户端程序与hadoop服务器之间正常通信需要开通的端口, 所以在hadoop各服务器上使用iptables防火墙屏蔽了测试客户端程序的ip和所有端口。然后,根据报错信息提示的端口号来逐步放开直到能正常通信下载文件。 在服务器端屏蔽指定ip访问所有端口 #查看…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

【Redis】笔记|第8节|大厂高并发缓存架构实战与优化
缓存架构 代码结构 代码详情 功能点: 多级缓存,先查本地缓存,再查Redis,最后才查数据库热点数据重建逻辑使用分布式锁,二次查询更新缓存采用读写锁提升性能采用Redis的发布订阅机制通知所有实例更新本地缓存适用读多…...

【p2p、分布式,区块链笔记 MESH】Bluetooth蓝牙通信 BLE Mesh协议的拓扑结构 定向转发机制
目录 节点的功能承载层(GATT/Adv)局限性: 拓扑关系定向转发机制定向转发意义 CG 节点的功能 节点的功能由节点支持的特性和功能决定。所有节点都能够发送和接收网格消息。节点还可以选择支持一个或多个附加功能,如 Configuration …...

LangFlow技术架构分析
🔧 LangFlow 的可视化技术栈 前端节点编辑器 底层框架:基于 (一个现代化的 React 节点绘图库) 功能: 拖拽式构建 LangGraph 状态机 实时连线定义节点依赖关系 可视化调试循环和分支逻辑 与 LangGraph 的深…...

【Elasticsearch】Elasticsearch 在大数据生态圈的地位 实践经验
Elasticsearch 在大数据生态圈的地位 & 实践经验 1.Elasticsearch 的优势1.1 Elasticsearch 解决的核心问题1.1.1 传统方案的短板1.1.2 Elasticsearch 的解决方案 1.2 与大数据组件的对比优势1.3 关键优势技术支撑1.4 Elasticsearch 的竞品1.4.1 全文搜索领域1.4.2 日志分析…...

深入浅出Diffusion模型:从原理到实践的全方位教程
I. 引言:生成式AI的黎明 – Diffusion模型是什么? 近年来,生成式人工智能(Generative AI)领域取得了爆炸性的进展,模型能够根据简单的文本提示创作出逼真的图像、连贯的文本,乃至更多令人惊叹的…...

[论文阅读]TrustRAG: Enhancing Robustness and Trustworthiness in RAG
TrustRAG: Enhancing Robustness and Trustworthiness in RAG [2501.00879] TrustRAG: Enhancing Robustness and Trustworthiness in Retrieval-Augmented Generation 代码:HuichiZhou/TrustRAG: Code for "TrustRAG: Enhancing Robustness and Trustworthin…...
