当前位置： 首页 > news >正文

京东pop店铺订单导出

news 2025/9/19 21:52:17

下载安装与运行

下载、安装与运行 · 语雀

特别提醒

  1. 只能导出已登录店铺的订单
  2. 导出的收件人手机号是虚拟号

功能

主要是方便线下工厂发货的店主

  • 所见即所得的导出
  • 自由选择导出项
  • 自由排序Excel导出列顺序
  • 导出过程中有进度提示，用户可以随时提前中止

什么是所见即所得

你当前列出了哪些订单，软件导出的就是哪些订单

列出订单的两种方式

  • 使用条件精确查询
  • 按类型列出，如导出待出库

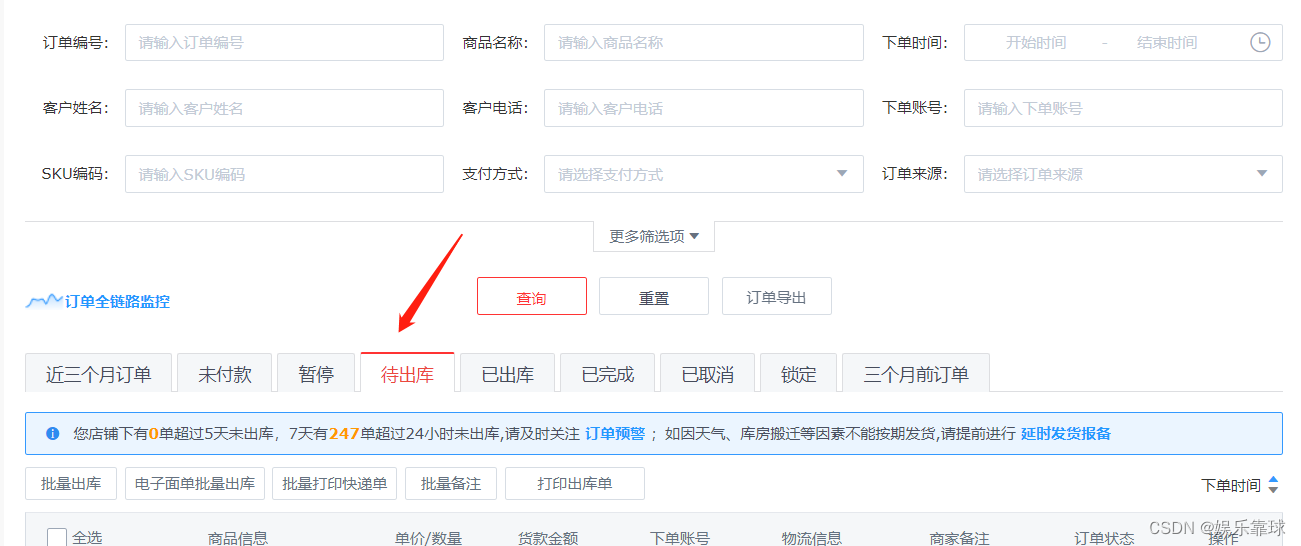
 精确查询后再导出

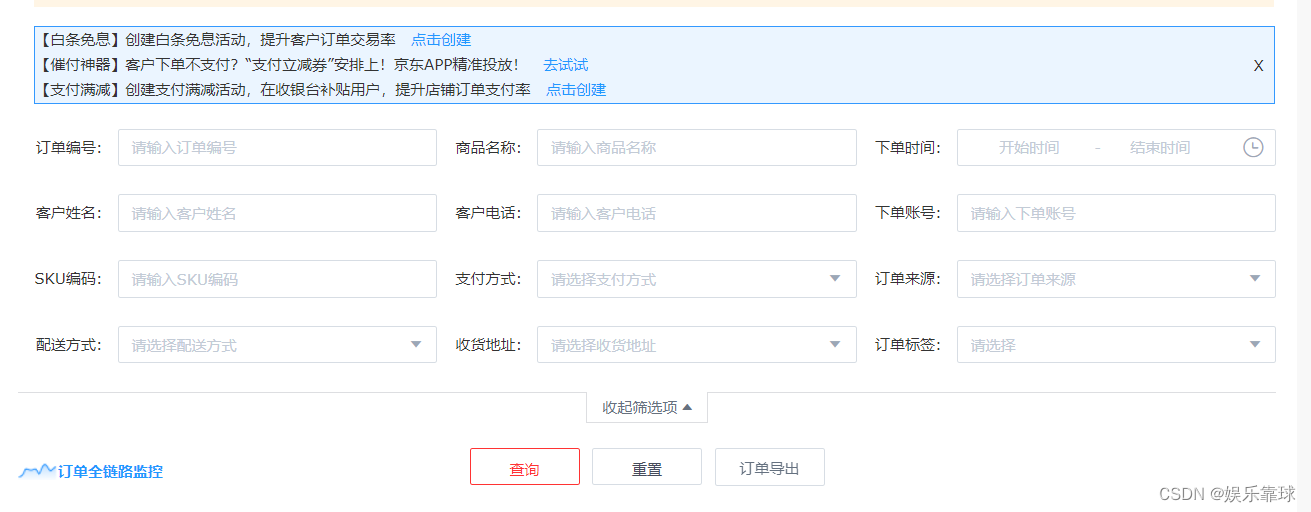
支持的导出数据项

用户可以根据实际情况，只选择自己需要的，导出结果更简洁

 

订单导出步骤

  1. 从应用列表找到京东商家订单导出
  2. 进入后登录店铺，筛选好需要导出的订单
  3. 选择要导出的数据项
  4. 起个文件名保存即可

下面以导出一个具体的订单为例，演示整个过程

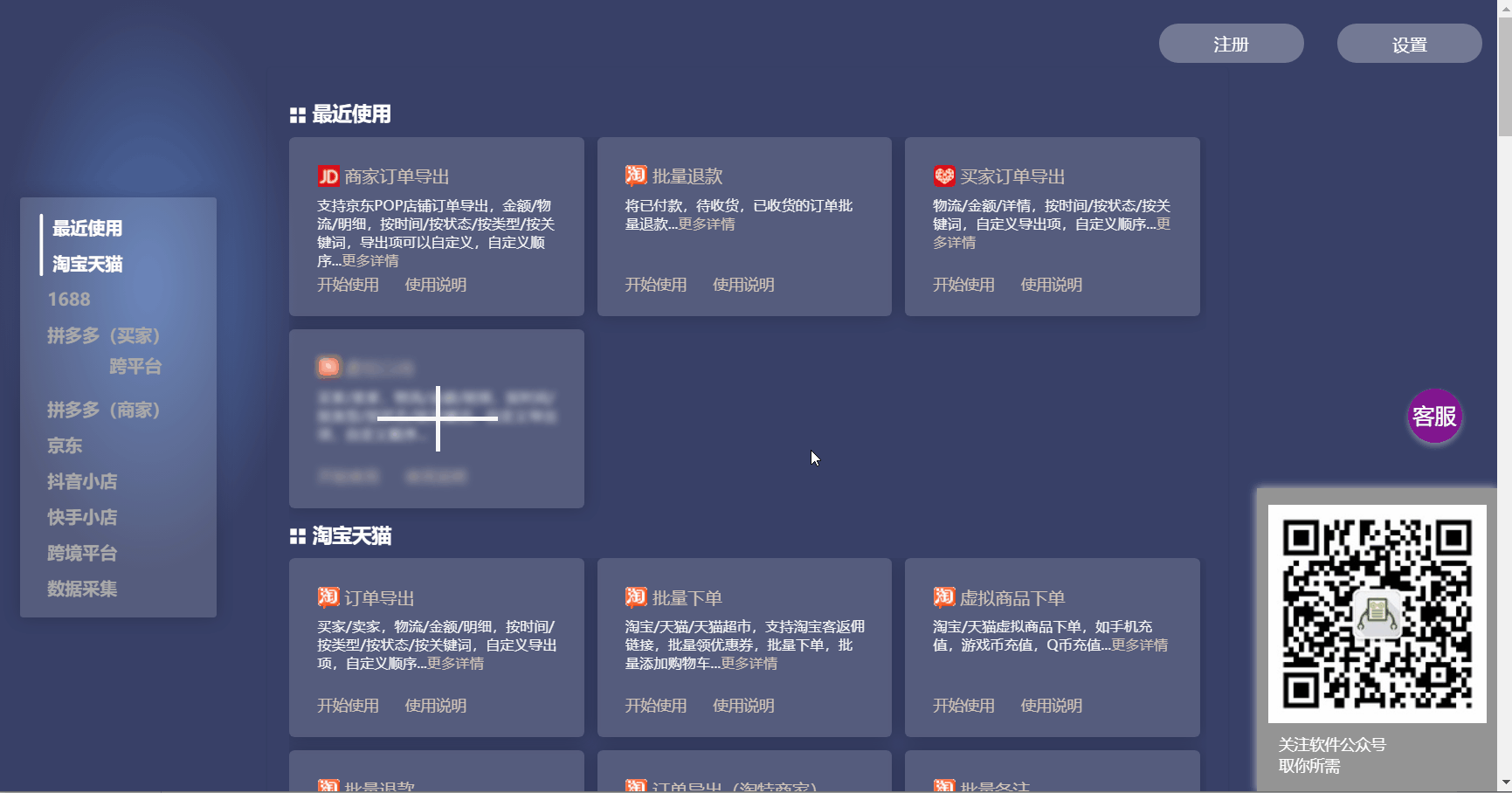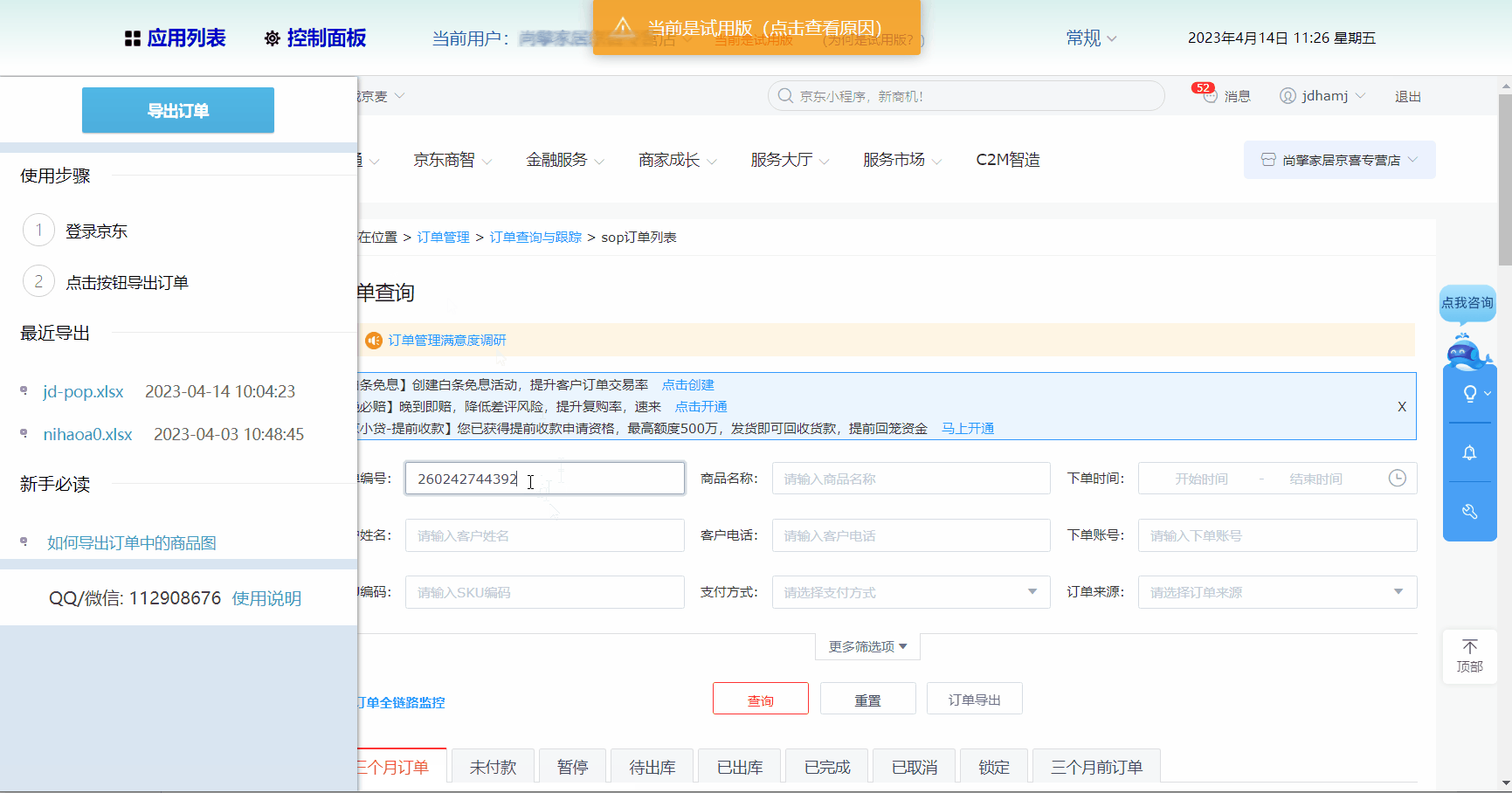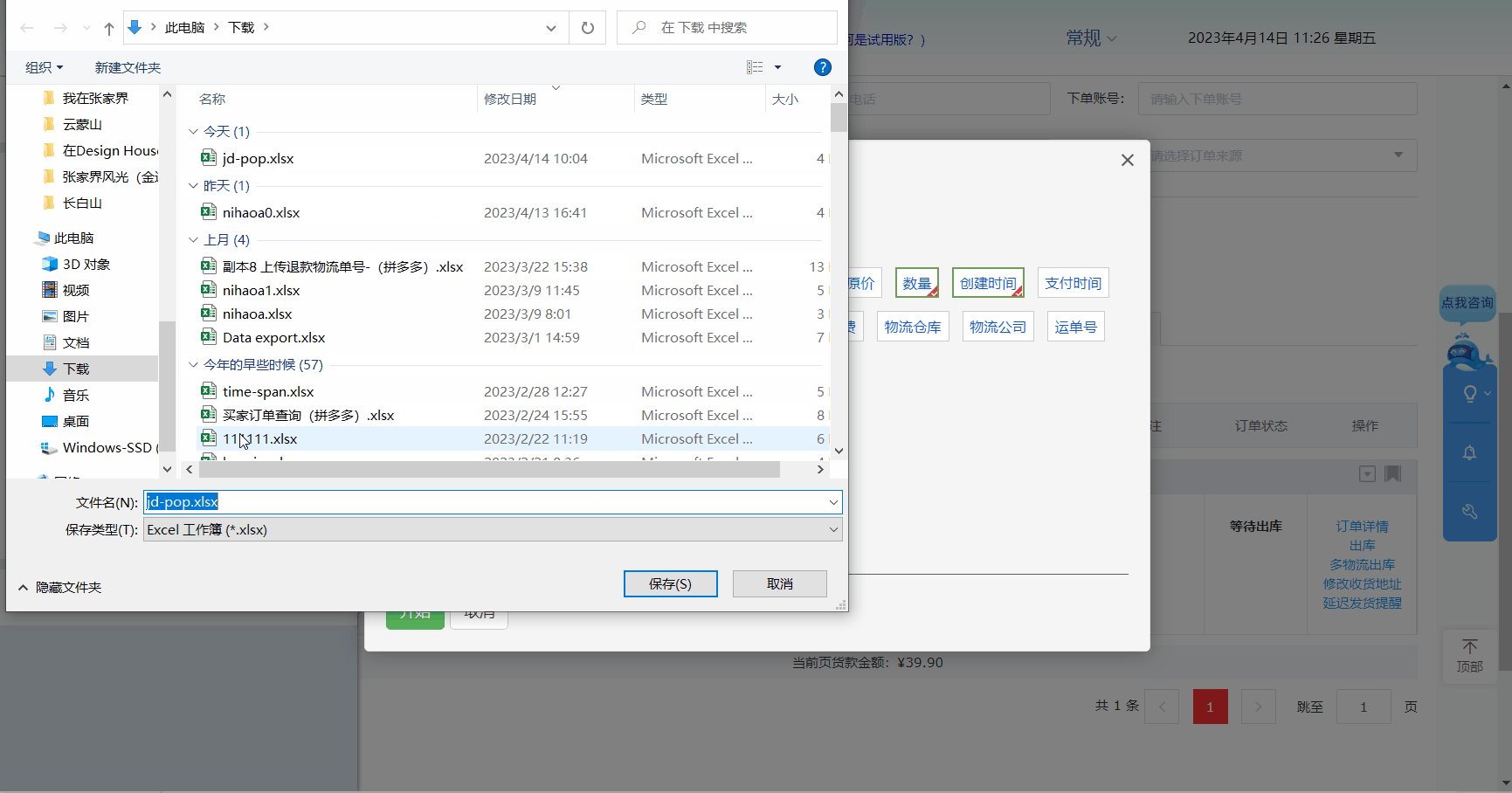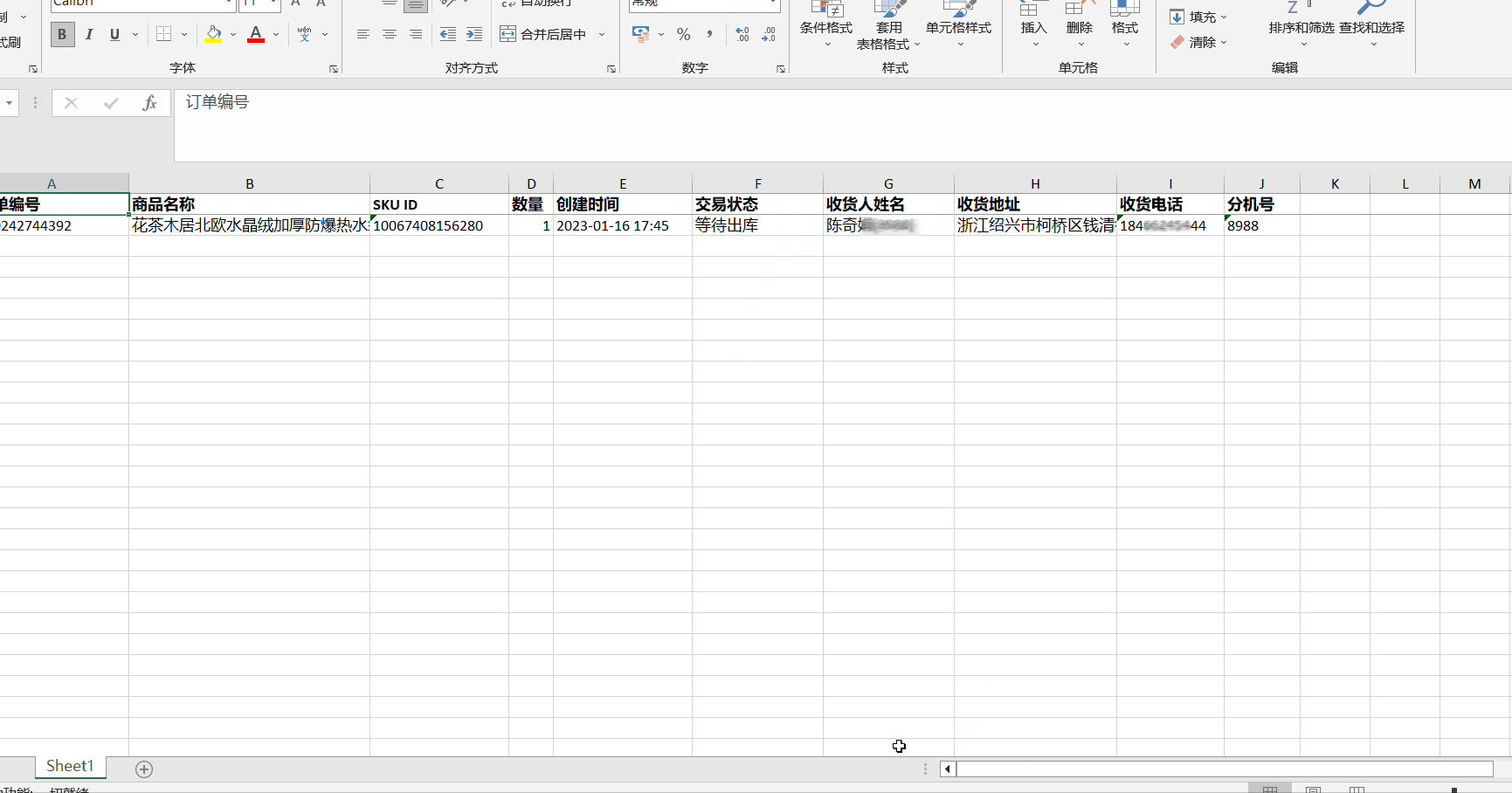
 常见问题

软件是否安全

安全，因为软件完全等同于用户操作鼠标键盘，复制粘贴到Excel

另外，软件只需要用户登录自己店铺，而不需要登录第三方平台，所有的数据只在自己的电脑与京东平台间流动

相关文章：

京东pop店铺订单导出

下载安装与运行 下载、安装与运行 语雀 特别提醒 只能导出已登录店铺的订单导出的收件人手机号是虚拟号 功能 主要是方便线下工厂发货的店主 所见即所得的导出自由选择导出项自由排序Excel导出列顺序导出过程中有进度提示，用户可以随时提前中止 什么是所见即所…...

编程日记 2023/4/14 19:56:10

论文阅读：Towards Stable Test-time Adaptation in Dynamic Wild World

今天阅读ICLR 2023 ——Towards Stable Test-time Adaptation in Dynamic Wild World Keywords：Test-time adaptation (TTA)； 文章目录Towards Stable Test-time Adaptation in Dynamic Wild WorldProblem：motivation：Contributio…...

编程日记 2023/4/14 19:51:08

2022国赛27：Linux-1时间服务chrony配置

大赛试题内容： 3.利用chrony配置Linux-1为其他Linux主机提供时间同步服务。 解答过程： 安装chrony服务[root@cs1 ~]# yum -y install chrony 配置/etc/chrony.conf文件[root@cs1 ~]# vi /etc/chrony.conf 7行改为 server 10.10.70.101 iburst 23行改为 去掉#号 allow 1…...

编程日记 2023/4/14 19:46:06

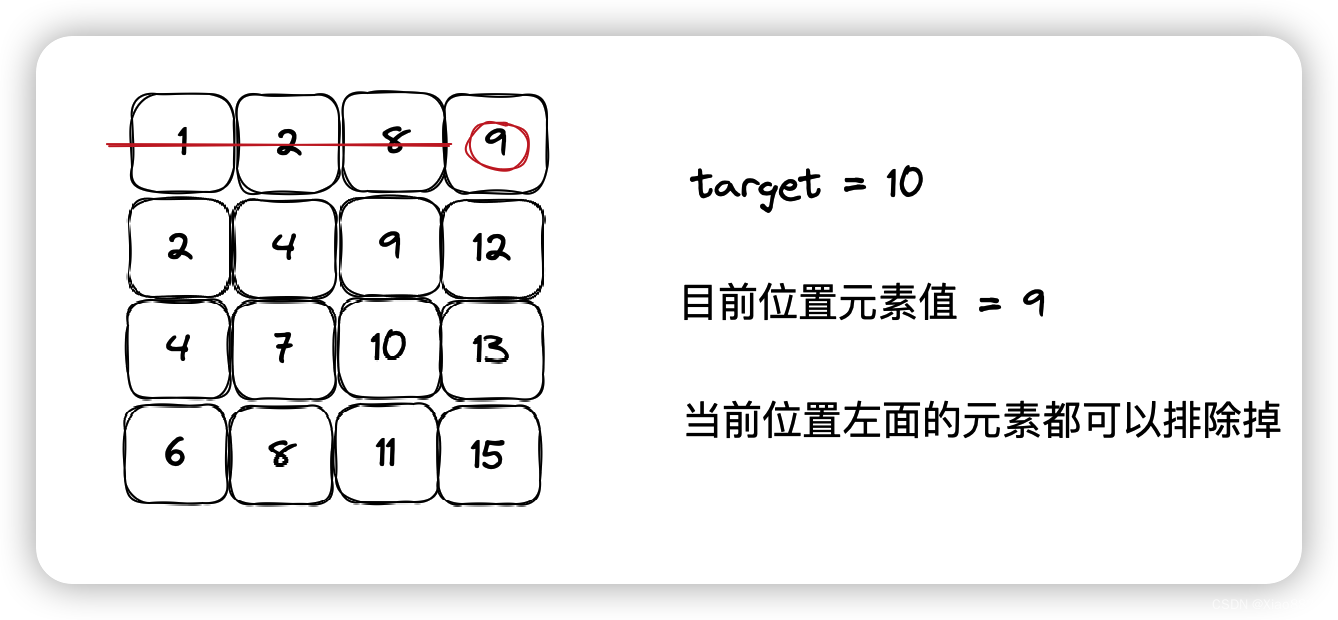
Java——二维数组中的查找

题目链接 牛客在线oj题——二维数组中的查找 题目描述 在一个二维数组array中（每个一维数组的长度相同），每一行都按照从左到右递增的顺序排序，每一列都按照从上到下递增的顺序排序。请完成一个函数，输入这样的一个二…...

编程日记 2023/5/29 22:14:29

Android 9.0 添加关机铃声功能实现

1.前言 在9.0的系统rom定制化开发中,在原生系统中，关于开机铃声和关机铃声是默认不支持的，系统默认支持开机动画和关机动画等功能，所以关于增加开机铃声和关机 铃声的相关功能，需要自己增加相关的关机铃声功能 2.添加关机铃声功能实现的核心类 frameworks\base\cmds\boo…...

编程日记 2023/4/14 19:36:03

IPv4 和 IPv6 的组成结构和对比

IPv4 和 IPv6 的组成结构和对比IPv4IPv6互联网协议 (IP) 是互联网通信的基础，IP 地址是互联网上每个设备的唯一标识符。目前最常用的 IP 协议是 IPv4，它已经有近 30 年的历史了。然而，IPv4 存在一些问题，例如: 地址空间不足:IPv4 …...

编程日记 2023/4/14 19:31:02

Spring的事务管理

Spring的事务管理Spring的事务管理1、事务的回顾【1】事务的定义【2】事务的ACID原则2、spring事务API介绍【了解】【1】PlatformTransactionManager【1.1】PlatformTransactionManager作用【1.2】PlatformTransactionManager接口【1.3】PlatformTransactionManager实现类【2】…...

编程日记 2023/4/14 19:26:01

MCAL知识点（十六）：VADC驱动配置详解（理论基础篇）

目录 1、概述 2、EB配置 2.1、通用界面配置 2.1.1、General 2.1.2、AdcConfigSet_0 2.1.3、AdcGlobinputClass 2.1.4、AdcHwUn...

编程日记 2023/4/14 19:20:59

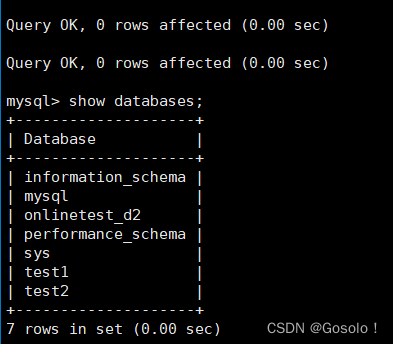
MySQL--库的操作--校验规则对于数据库的影响--0409

目录 1.库的基础操作 查看数据库 创建数据库 删除数据库 查看建库语句 修改数据库 2.字符集和字符集校验规则 2.1 查看系统默认字符集以及校验规则 2.2 使用特定的字符集创建数据库 2.3 不同校验规则对数据库的影响 2.3.1 大小写验证 2.3.2 排序验证 3.备份和恢复 3.1…...

编程日记 2023/4/14 19:15:58

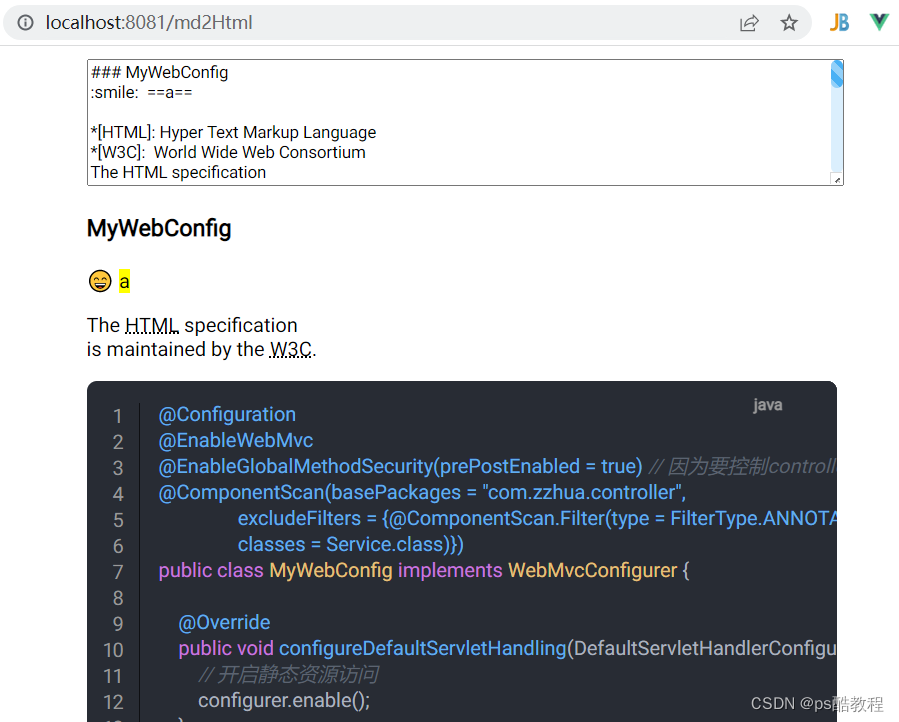
markdown-it基本使用

markdown-it能够将markdown语法的内容转换为html内容，这样我们使用markdown语法写的笔记，就可以转换作为网页使用了 Markdown语法 Markdown语法图文全面详解(10分钟学会) 基础使用 安装markdown-it npm install markdown-it --save使用markdown-it …...

编程日记 2023/4/14 19:10:57

CMake入门教程【核心篇】8.3对象库

文章目录 知识点实例代码目录代码实现知识点 add_library(libhello OBJECT src/hello.cpp)使用OBJECT 参数可以把对象传入到libhello 中，且不会生成.lib文件 使用变量$<TARGET_OBJECTS:libhello>即可获取，比较实用 实例 代码目录 |-📁prj10   |-- 🎴CMakeLists…...

编程日记 2023/4/14 19:05:56

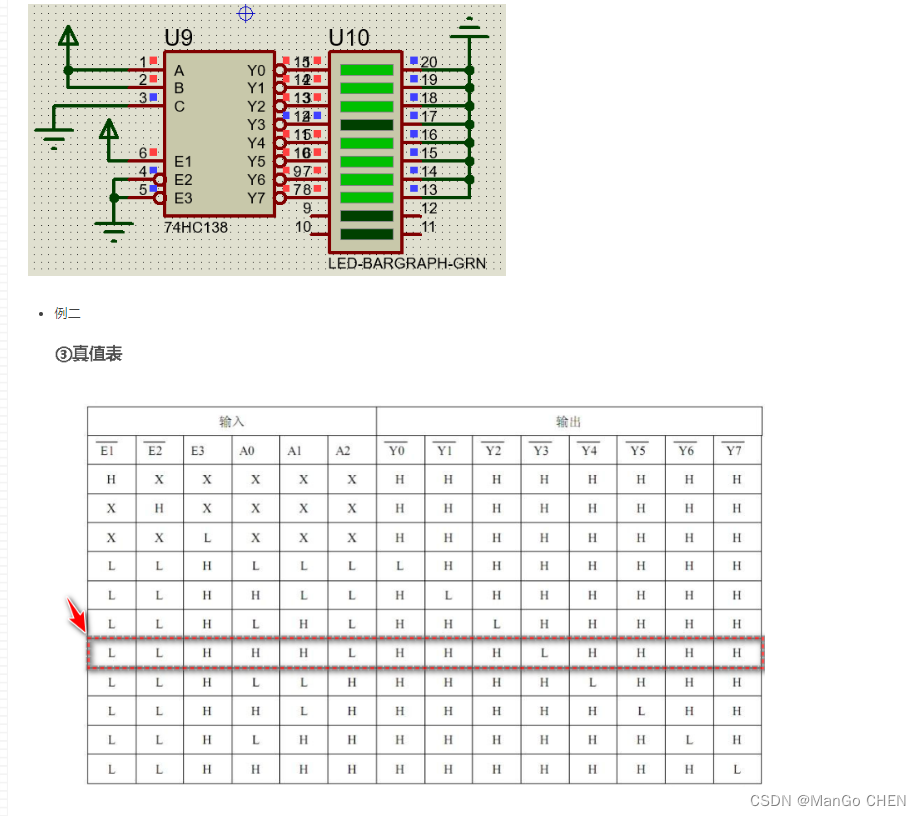
单片机_CT107D训练平台电路原理图\蓝桥杯训练板\IO扩展模块\74HC138译码器

74HC138译码器&#xff08;实现3个IO口控制8个引脚实现IO口的扩展&#xff09; 配置信号放大模块&#xff0c;可以对输入的低电压模拟信号进行放大&#xff1b; 配置 138 译码器&#xff0c;可以做译码实验&#xff1b; 外设可以用存储器映射方式访问&#xff0c;也可以直接控…...

编程日记 2023/4/14 19:00:54

Rabbitmq消息确认机制

1.生产者确认机制 确认消息发送到交换机--Confirm方式 1.1普通Confirm方式 private static void sendMsg(Channel channel) throws IOException, InterruptedException { //开启确认机制 channel.confirmSelect(); //发送消息到exchange St…...

编程日记 2023/4/14 18:55:53

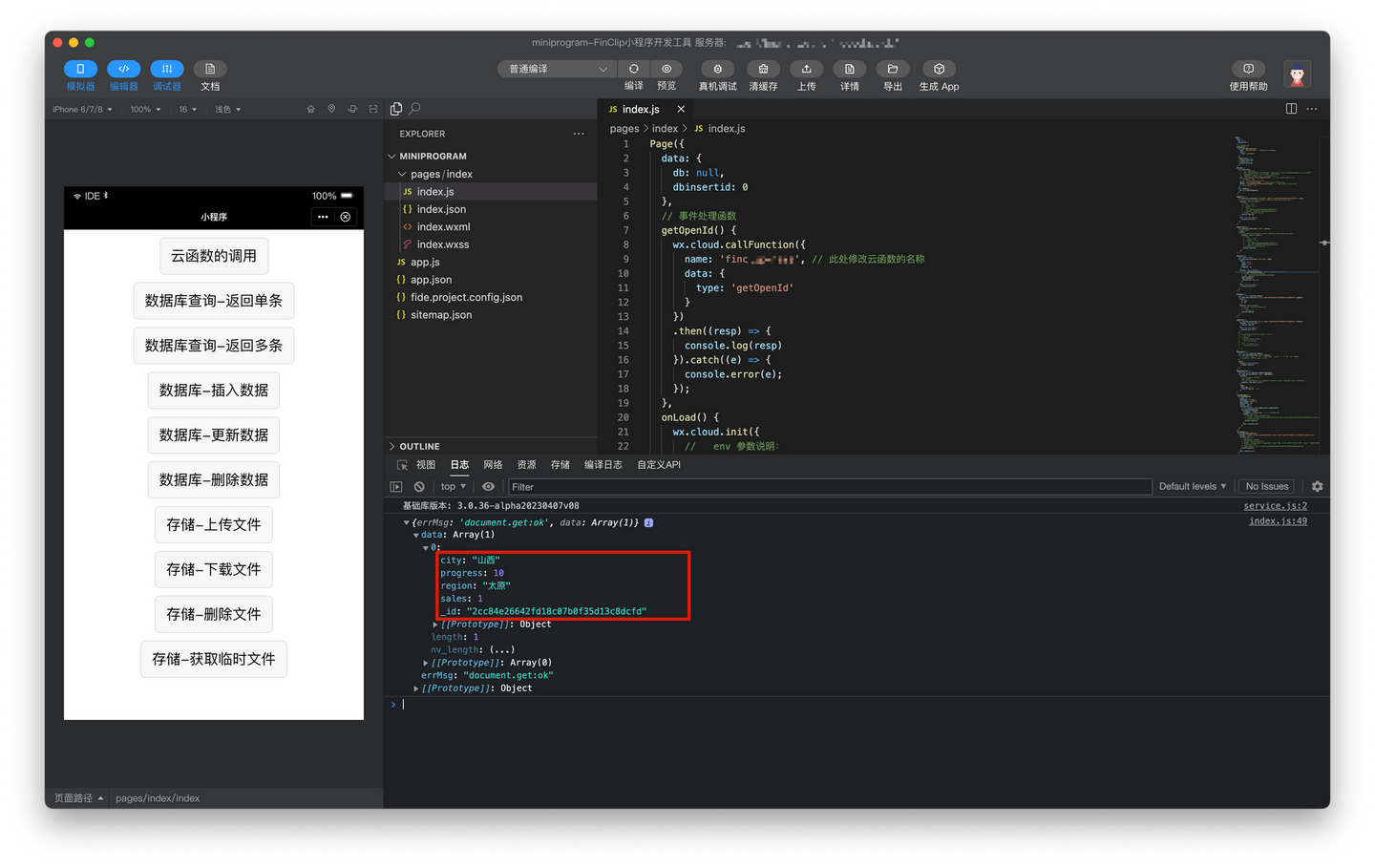
FinClip 云开发实践（附小程序demo）

在开发一个小程序时&#xff0c;除了考虑界面功能逻辑外&#xff0c;还需要后端的数据支持&#xff0c;开发者需要提前考虑服务器、存储和数据库等相关需求的支持能力&#xff0c;此外还可能需要花费时间精力在部署应用、和依赖服务的建设上。 ​ 因此&#xff0c;腾讯小程序为…...

编程日记 2023/4/14 18:50:52

真正好用的工业品ERP系统应该是什么样的？

一个好用的进销存ERP系统应该有以下特点&#xff1a; 1. 全面覆盖企业经营流程&#xff0c;包括采购、销售、库存、财务等模块&#xff0c;能够实现全方位的管理和控制。 2. 自定义配置&#xff0c;灵活地适应大多数用户的需求。 3. 数据精准、实时化&#xff0c;支持统计分…...

编程日记 2023/4/14 18:45:50

Shiro重定向

使用了统一认证&#xff0c;然后每次登录&#xff0c;不能定向到用户指定的界面&#xff0c;非得回到首页&#xff0c;所以做了如下改动 1、在FormAuthenticationFilter中在issueSuccessRedirect中加上五句话。 Overrideprotected void issueSuccessRedirect(ServletRequest …...

编程日记 2023/4/14 18:40:49

Greenplum数据库执行器——PartitionSelector执行节点

为了能够对分区表有优异的处理能力&#xff0c;对于查询优化系统来说一个最基本的能力就是做分区裁剪partition pruning&#xff0c;将query中并不涉及的分区提前排除掉。如下执行计划所示&#xff0c;由于单表谓词在parititon key上&#xff0c;在优化期间即可确定哪些可以分区…...

编程日记 2023/4/14 18:35:48

POJ 2311 Cutting Game

POJ 2311 Cutting Game 题目大意 有一张有whw\times hwh个格子的长方形纸张&#xff0c;两个人轮流将当前的纸张中选一张&#xff0c;并沿着格子的边界将这张纸剪成两部分。最先切出只有一个格子的纸张&#xff08;111\times 111的纸张&#xff09;的玩家获胜。当双方都采用最…...

编程日记 2023/4/14 18:30:47

CTF-PHP反序列化漏洞1-基础知识

作者&#xff1a;Eason_LYC 悲观者预言失败&#xff0c;十言九中。 乐观者创造奇迹&#xff0c;一次即可。 一个人的价值&#xff0c;在于他所拥有的。可以不学无术&#xff0c;但不能一无所有&#xff01; 技术领域&#xff1a;WEB安全、网络攻防 关注WEB安全、网络攻防。我的…...

编程日记 2023/4/14 18:25:45

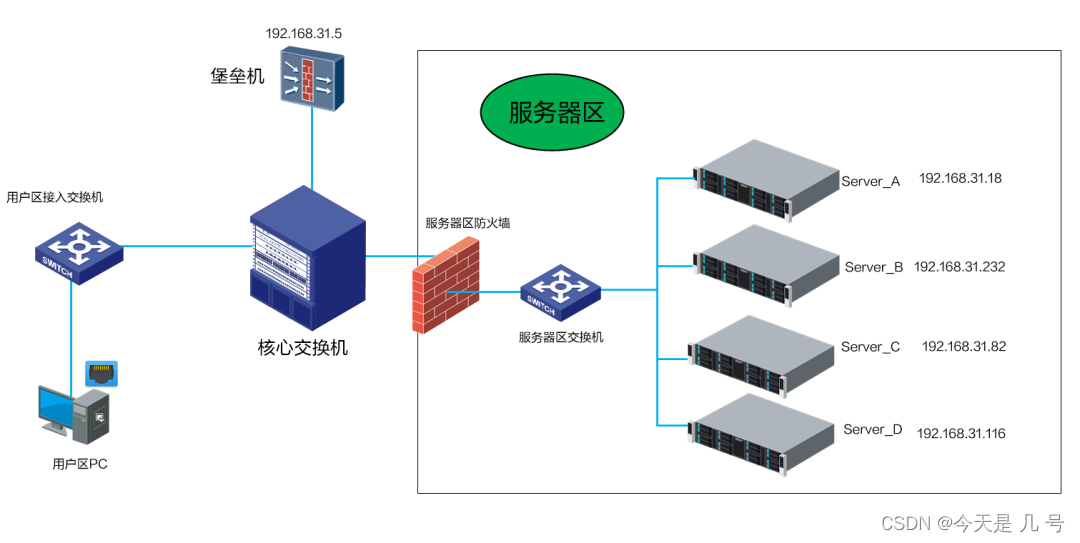
【面试】记一次安恒面试及总结

文章目录SQL 注入sql注入的原理&#xff1f;如何通过SQL注入判断对方数据库类型&#xff1f;补充一下其他方法判断数据库类型时间盲注的函数XPath注入抓不到http/https包&#xff0c;怎么办&#xff1f;app无自己的ssl证书app有自己的ssl证书-证书绑定(SSL pinning)逻辑漏洞有哪…...

编程日记 2023/4/14 18:20:44

应用升级/灾备测试时使用guarantee 闪回点迅速回退

1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间&#xff0c; 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点&#xff0c;不需要开启数据库闪回。…...

编程新知 2025/7/30 7:20:17

ubuntu搭建nfs服务centos挂载访问

在Ubuntu上设置NFS服务器 在Ubuntu上&#xff0c;你可以使用apt包管理器来安装NFS服务器。打开终端并运行&#xff1a; sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享&#xff0c;例如/shared&#xff1a; sudo mkdir /shared sud…...

编程新知 2025/8/27 13:05:41

【机器视觉】单目测距——运动结构恢复

ps&#xff1a;图是随便找的&#xff0c;为了凑个封面 前言 在前面对光流法进行进一步改进&#xff0c;希望将2D光流推广至3D场景流时&#xff0c;发现2D转3D过程中存在尺度歧义问题&#xff0c;需要补全摄像头拍摄图像中缺失的深度信息&#xff0c;否则解空间不收敛&#xf…...

编程新知 2025/9/11 12:54:40

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序

一、开发环境准备 ​​工具安装​​&#xff1a; 下载安装DevEco Studio 4.0&#xff08;支持HarmonyOS 5&#xff09;配置HarmonyOS SDK 5.0确保Node.js版本≥14 ​​项目初始化​​&#xff1a; ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

编程新知 2025/7/22 6:12:57

【HarmonyOS 5 开发速记】如何获取用户信息（头像/昵称/手机号）

1.获取 authorizationCode&#xff1a; 2.利用 authorizationCode 获取 accessToken&#xff1a;文档中心 3.获取手机&#xff1a;文档中心 4.获取昵称头像&#xff1a;文档中心 首先创建 request 若要获取手机号&#xff0c;scope必填 phone&#xff0c;permissions 必填 …...

编程新知 2025/9/17 2:39:21

项目部署到Linux上时遇到的错误（Redis，MySQL，无法正确连接，地址占用问题）

Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败&#xff0c;具体原因是客户端发送了密码认证请求&#xff0c;但Redis服务器未设置密码 1.为Redis设置密码&#xff08;匹配客户端配置&#xff09; 步骤&#xff1a; 1&#xff09;.修…...

编程新知 2025/9/7 8:51:02

算法笔记2

1.字符串拼接最好用StringBuilder&#xff0c;不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

编程新知 2025/9/13 17:42:29

MySQL账号权限管理指南：安全创建账户与精细授权技巧

在MySQL数据库管理中&#xff0c;合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号&#xff1f; 最小权限原则&#xf…...

编程新知 2025/9/5 23:36:27

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案

这个问题我看其他博主也写了&#xff0c;要么要会员、要么写的乱七八糟。这里我整理一下&#xff0c;把问题说清楚并且给出代码&#xff0c;拿去用就行&#xff0c;照着葫芦画瓢。 问题 在继承QWebEngineView后&#xff0c;重写mousePressEvent或event函数无法捕获鼠标按下事…...

编程新知 2025/6/11 3:07:32

JavaScript基础-API 和 Web API

在学习JavaScript的过程中&#xff0c;理解API&#xff08;应用程序接口&#xff09;和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能&#xff0c;使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...

编程新知 2025/8/21 23:03:46