Leetcode.2601 质数减法运算
题目链接
Leetcode.2601 质数减法运算 Rating : 1779
题目描述
给你一个下标从 0 开始的整数数组 nums,数组长度为 n 。
你可以执行无限次下述运算:
- 选择一个之前未选过的下标 i ,并选择一个 严格小于
nums[i]的质数 ppp ,从nums[i]中减去 ppp 。
如果你能通过上述运算使得nums成为严格递增数组,则返回true;否则返回false。
严格递增数组 中的每个元素都严格大于其前面的元素。
示例 1:
输入:nums = [4,9,6,10]
输出:true
解释:
在第一次运算中:选择 i = 0 和 p = 3 ,然后从 nums[0] 减去 3 ,nums 变为 [1,9,6,10] 。
在第二次运算中:选择 i = 1 和 p = 7 ,然后从 nums[1] 减去 7 ,nums 变为 [1,2,6,10] 。
第二次运算后,nums 按严格递增顺序排序,因此答案为 true 。
示例 2:
输入:nums = [6,8,11,12]
输出:true
解释:nums 从一开始就按严格递增顺序排序,因此不需要执行任何运算。
示例 3:
输入:nums = [5,8,3]
输出:false
解释:可以证明,执行运算无法使 nums 按严格递增顺序排序,因此答案是 false 。
提示:
- 1<=nums.length<=10001 <= nums.length <= 10001<=nums.length<=1000
- 1<=nums[i]<=10001 <= nums[i] <= 10001<=nums[i]<=1000
- nums.length==nnums.length == nnums.length==n
解法:筛素数 + 贪心 + 二分
由于 nums[i]nums[i]nums[i] 最大都只有 10310^3103,所以我们可以把 100010001000以内的素数预处理出来,存入 primesprimesprimes 数组中。
从后往前开始贪心,假设当前遍历到 nums[i]nums[i]nums[i] 了(i>0i > 0i>0):
- 如果 nums[i]>nums[i−1]nums[i] > nums[i-1]nums[i]>nums[i−1],符合递增的要求,之间跳过本次循环
- 否则 nums[i]≤nums[i−1]nums[i] \leq nums[i-1]nums[i]≤nums[i−1],我们将 nums[i−1]−nums[i]nums[i-1] - nums[i]nums[i−1]−nums[i] 的差值,记作 ddd:
-
- 我们通过 二分 的方式,从 primesprimesprimes 中找到第一个大于 ddd 的质数 ppp。
-
- 当 nums[i−1]>pnums[i-1] > pnums[i−1]>p 的情况下,nums[i−1]nums[i-1]nums[i−1] 才能减去 ppp ,否则返回 falsefalsefalse
- 循环结束返回 truetruetrue
时间复杂度: O(nlogn)O(nlogn)O(nlogn)
C++代码:
vector<int> primes;
const int N = 1e3+10;auto get_prime = [](){bool st[N + 1] = {};for(int i = 2;i <= N;i++){if(!st[i]) primes.push_back(i);for(auto p:primes){if(i * p > N) break;st[i * p] = true;if(i % p == 0) break;}}return 0;
}();class Solution {
public:bool primeSubOperation(vector<int>& nums) {int n = nums.size();for(int i = n - 1;i > 0;i--){if(nums[i] > nums[i-1]) continue;int d = nums[i-1] - nums[i];int idx = upper_bound(primes.begin(),primes.end(),d) - primes.begin();if(nums[i-1] > primes[idx]) nums[i - 1] -= primes[idx];else return false;}return true;}
};相关文章:

Leetcode.2601 质数减法运算
题目链接 Leetcode.2601 质数减法运算 Rating : 1779 题目描述 给你一个下标从 0 开始的整数数组 nums,数组长度为 n 。 你可以执行无限次下述运算: 选择一个之前未选过的下标 i ,并选择一个 严格小于 nums[i]的质数 ppp &…...

DP7416国产192K数字音频接收芯片兼容替代CS8416
目录192K 数字音频应用DP7416简介芯片特性192K 数字音频应用 采样率192khz,能将192,000hz以下的频率都录下来,而且对声波每秒连续采样192,000次。在回放的时候,这192,000个采样点按顺序播放,从而还原原来的声音。 过采样技术除…...
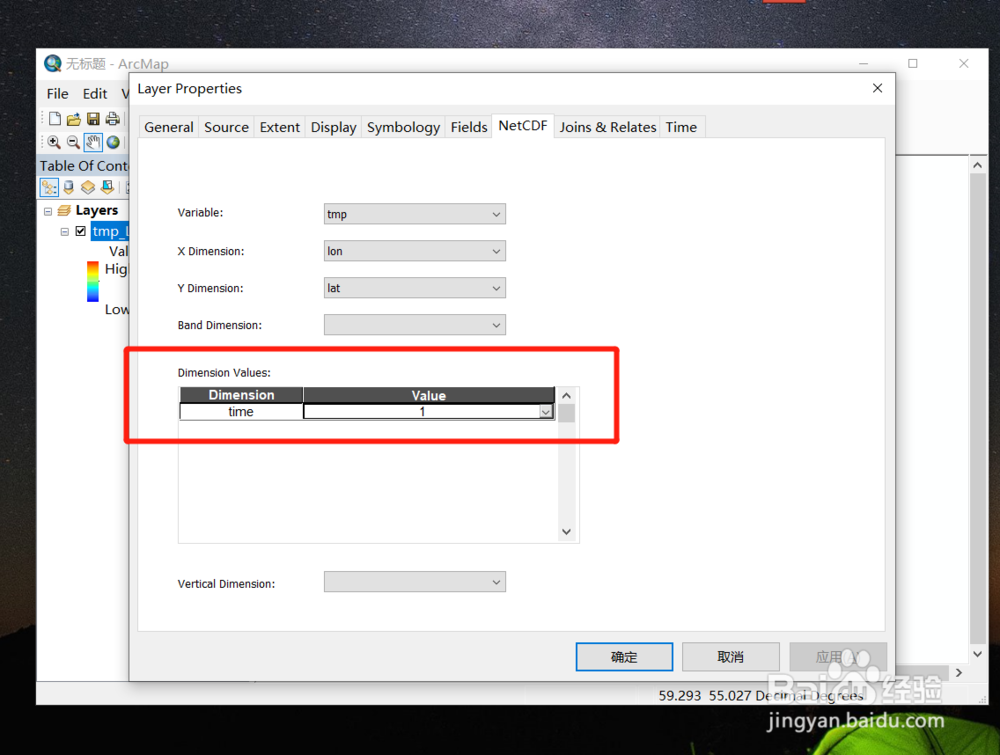
全球土壤湿度数据获取方法
土壤湿度亦称土壤含水率,表示土壤干湿程度的物理量。是土壤含水量的一种相对变量。通常用土壤含水量占干土重的百分数是示,亦称土壤质量湿度,如用土壤水分容积占土壤总容积的百分数表示,则称土壤容积湿度。通常说的土壤湿度&#…...
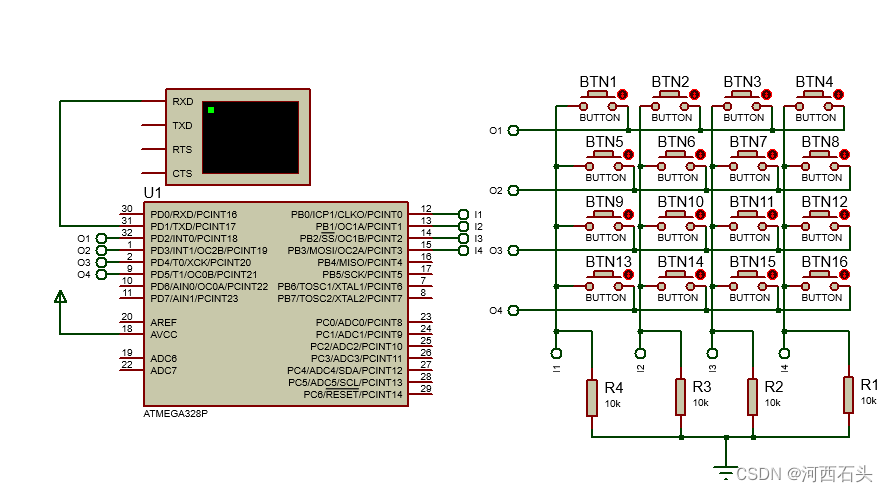
在proteus中仿真arduino实现矩阵键盘程序
矩阵键盘是可以解决我们端口缺乏的问题,当然,如果我们使用芯片来实现矩阵键盘的输入端口缺乏的问题将更加划算了,本文暂时不使用芯片来解决问题,而使用纯朴的8根线来实现矩阵键盘,目的是使初学者掌握原理。想了解使用芯…...

【ROS2指南-5】理解ROS2服务
目标:使用命令行工具了解 ROS 2 中的服务。 教程级别:初学者 时间: 10分钟 内容 背景 先决条件 任务 1 设置 2 ros2服务列表 3 ros2服务类型 4 ros2 服务查找 5 ros2界面展示 6 ros2 服务调用 概括 下一步 相关内容 背景 服务是 …...
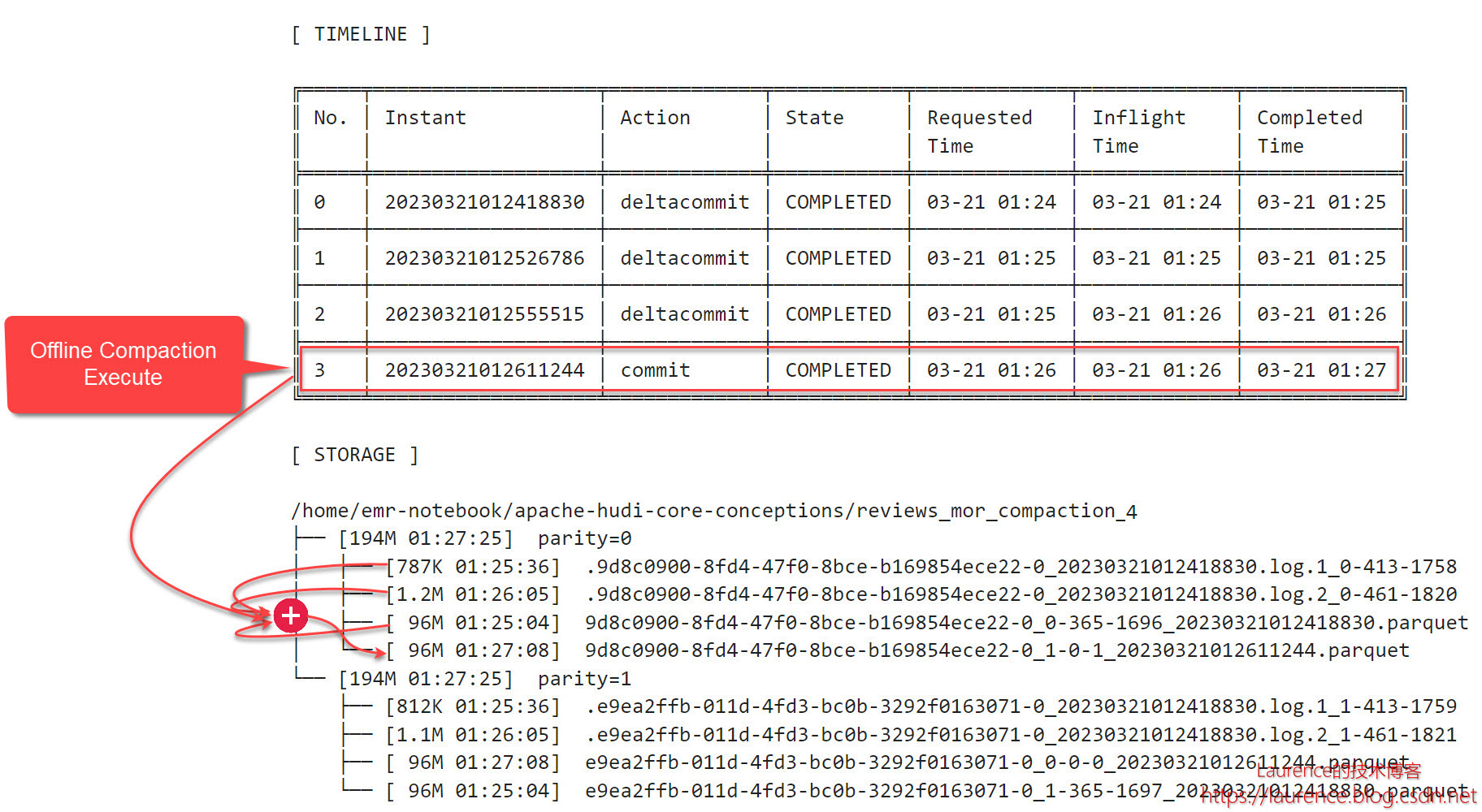
探索Apache Hudi核心概念 (3) - Compaction
Compaction是MOR表的一项核心机制,Hudi利用Compaction将MOR表产生的Log File合并到新的Base File中。本文我们会通过Notebook介绍并演示Compaction的运行机制,帮助您理解其工作原理和相关配置。 1. 运行 Notebook 本文使用的Notebook是:《A…...

100Wqps异地多活,得物是怎么架构的?
说在前面 在40岁老架构师尼恩的数千读者群中,一直在指导大家简历和职业升级,前几天,指导了一个华为老伙伴的简历,小伙伴的优势在异地多活,但是在简历指导的过程中,尼恩发现: 异地多活的概念、异…...

35岁的测试工程师被公司强行辞退,感叹道:我以前就该好好努力了
曾经的高薪软件测试工程师,今年35岁了,被公司劝退了,外卖跑到凌晨,很累,但还是有一种想诉说的冲动。哪怕让大家觉得已经说得太多了,烦了,都成祥林嫂了,但是,我是真的想说…...
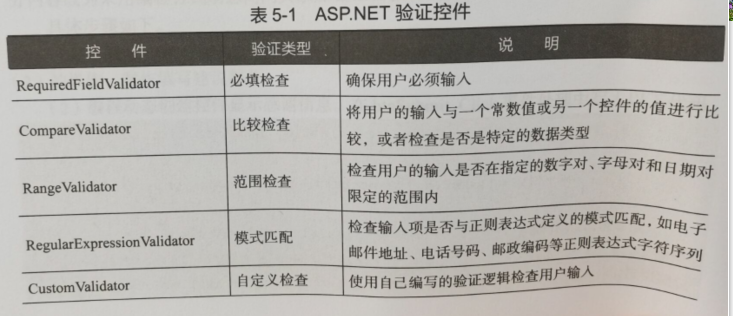
ASP.NET动态Web开发技术第5章
第5章数据验证一.预习笔记 1.验证控件概述: 2.RequiredFieldValidator(必填验证) 常用属性1:ControlToValidator:被验证的输入控件的ID 常用属性2:Text:验证失败时,验证控件显示的文本 常用…...
【数据结构与算法篇】时间复杂度与空间复杂度
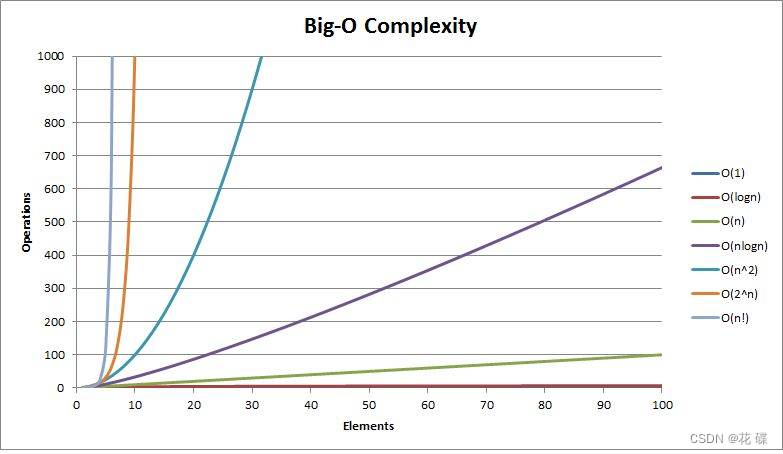
目录 一、数据结构和算法 1.什么是数据结构? 2.什么是算法? 3.数据结构和算法的重要性 二、算法的时间复杂度和空间复杂度 1.算法效率 2.算法的复杂度 3.复杂度在校招中的考察 4.时间复杂度 5.空间复杂度 6.常见复杂度对比 7.复杂度的OJ练…...
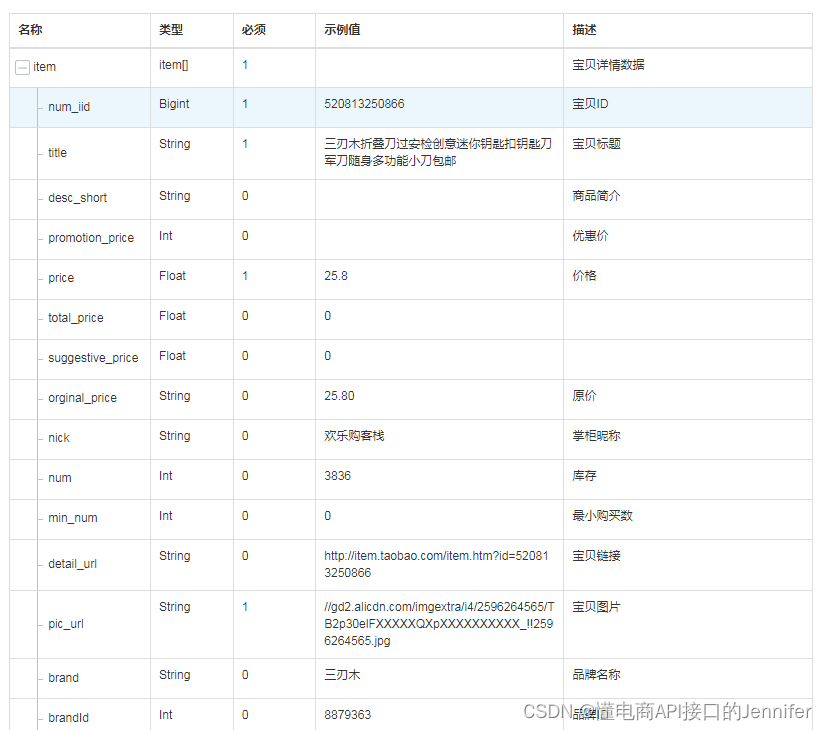
HTTP API接口设计规范
1. 所有请求使用POST方法 使用post,相对于get的query string,可以支持复杂类型的请求参数。例如日常项目中碰到get请求参数为数组类型的情况。 便于对请求和响应统一做签名、加密、日志等处理 2. URL规则 URL中只能含有英文,使用英文单词或…...
)
数据一致性校验(pt-table-checksum)
介绍 pt-table-checksum 和 pt-table-sync 是 percona 公司发布的、检查 MySQL 主从数据库数据一致性校验的工具。pt-table-checksum 利用 MySQL 复制原理,在主库执行校验和计算,并对比主从库校验和,由此判断主从库数据是否一致。如果发现数…...

Talk预告 | 新加坡国立大学郑奘巍 AAAI‘23 杰出论文:大批量学习算法加速推荐系统训练
本期为TechBeat人工智能社区第486期线上Talk! 北京时间3月30日(周四)20:00,新加坡国立大学二年级博士生——郑奘巍的Talk将准时在TechBeat人工智能社区开播! 他与大家分享的主题是: “大批量学习算法加速推荐系统训练”,届时将分…...
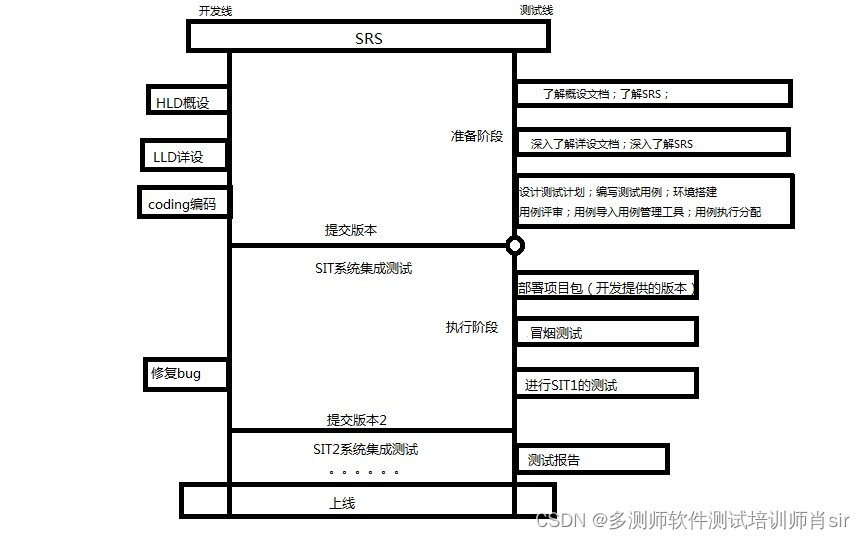
肖 sir_就业课__004项目流程(H模型)
项目流程: 一、面试提问(h模型) 1、你说下你们公司测试流程? 2、给你一个需求你会怎么做? 3、你讲下你的工作? 4、谈谈你是如何去测试? 答案:h模型 要求第一人称来写 讲解简化文字流程&#x…...
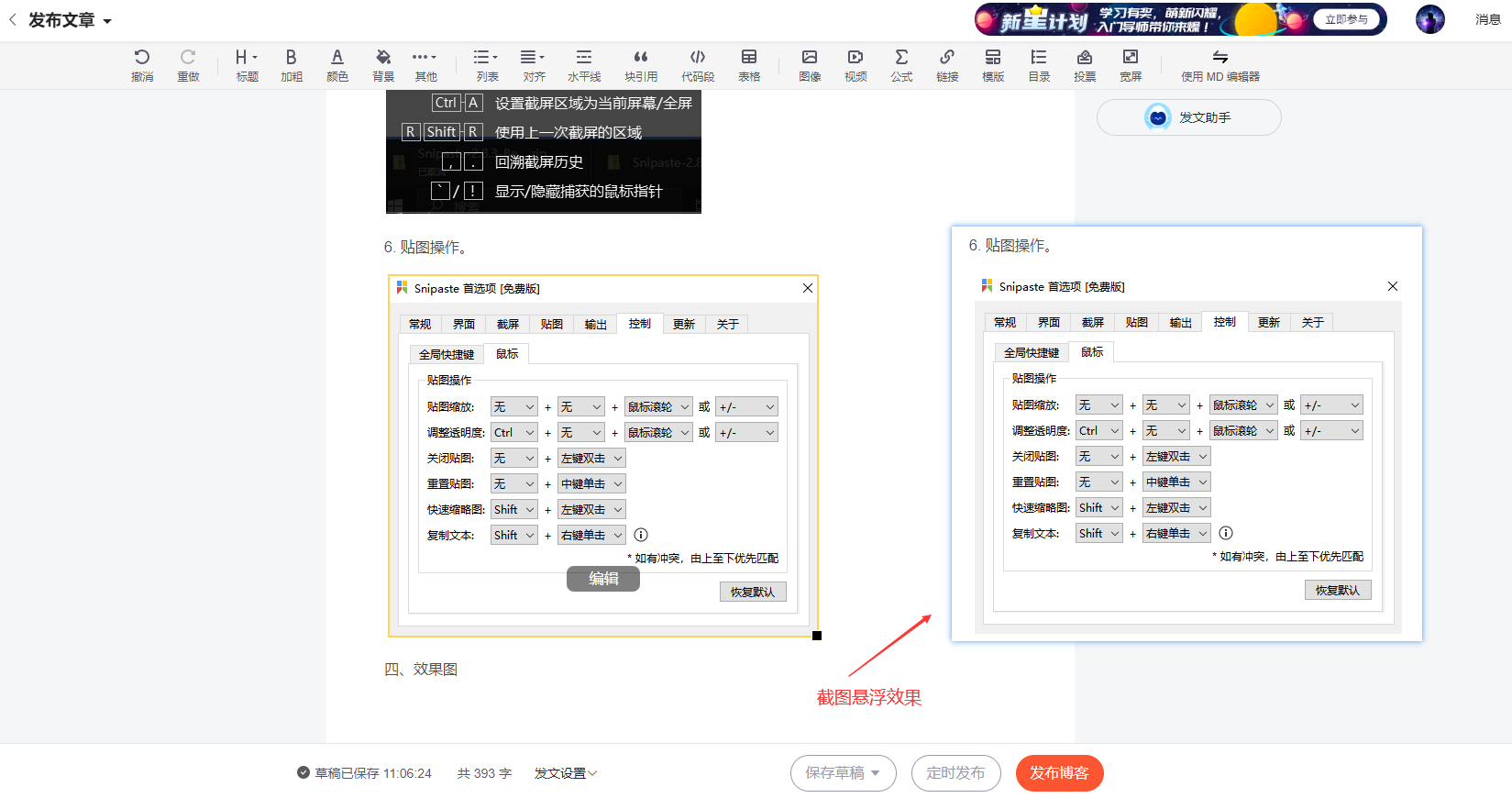
snipaste 截图工具——可以使图片悬浮在任何软件上,方便对比
一、下载 官网下载地址:Snipaste Downloads (需要梯子) CSDN下载地址:https://download.csdn.net/download/weixin_43042683/87671809 1. 下载 压缩包后,免安装,直接解压后既可以使用。 2. 点击Snipaste.…...

Docker 快速部署Springboot项目
编写Dockerfile文件 # Docker image for springboot file run # VERSION 0.0.1 # Author: # 基础镜像使用java FROM openjdk:8 # 作者 MAINTAINER laihx # VOLUME 指定了临时文件目录为/tmp。 # 其效果是在主机 /var/lib/docker 目录下创建了一个临时文件,并链接到…...

【LeetCode: 剑指 Offer II 112. 最长递增路径 | 递归 | DFS | 深度优先遍历 | 记忆化缓存表】
🍎作者简介:硕风和炜,CSDN-Java领域新星创作者🏆,保研|国家奖学金|高中学习JAVA|大学完善JAVA开发技术栈|面试刷题|面经八股文|经验分享|好用的网站工具分享💎💎💎 🍎座右…...
hive 入门 一般用于正式环境 修改元数据(二)
安装配置可参考 https://blog.csdn.net/weixin_43205308/article/details/130020674 1、如果启动过derby,最小初始化过 在安装路径下删除 derby.log metastore_db rm -rf derby.log metastore_db此处省略安装mysql数据库 2、配置MySQL 登录mysql mysql -uroot …...

在RedHat系统上使用firewall-cmd命令可以将端口打开
在RedHat系统上使用firewall-cmd命令可以将端口打开,具体操作如下: 首先,检查当前系统使用的防火墙服务,比如firewalld或iptables,使用以下命令: systemctl status firewalld # 检查firewalld服务 system…...
:免费可用的多种类 API 大全集合整理)
分享(五):免费可用的多种类 API 大全集合整理
前言 搜罗了各大平台整理了一波免费可以用的 API ,有需要的收藏起来啦。 实名认证 运营商二要素 API :运营商校验此姓名、手机号码是否一致。 运营商三要素 API:运营商验证姓名、身份证号码、手机号码是否一致,返回验证结果称…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...
的打车小程序)
基于鸿蒙(HarmonyOS5)的打车小程序
1. 开发环境准备 安装DevEco Studio (鸿蒙官方IDE)配置HarmonyOS SDK申请开发者账号和必要的API密钥 2. 项目结构设计 ├── entry │ ├── src │ │ ├── main │ │ │ ├── ets │ │ │ │ ├── pages │ │ │ │ │ ├── H…...
