【数据结构与算法篇】时间复杂度与空间复杂度

目录
一、数据结构和算法
1.什么是数据结构?
2.什么是算法?
3.数据结构和算法的重要性
二、算法的时间复杂度和空间复杂度
1.算法效率
2.算法的复杂度
3.复杂度在校招中的考察
4.时间复杂度
5.空间复杂度
6.常见复杂度对比
7.复杂度的OJ练习
👻内容专栏:《数据结构与算法》
🐨本文概括: 讲解数据结构和算法的概念、时间复杂度、空间复杂度、常见复杂度对比。
🐼本文作者:花 碟
🐸发布时间:2023.4.13
一、数据结构和算法
1.什么是数据结构?
数据结构(Data Structure)是计算机存储、组织数据的方式,指相互之间存在一种或多种特定关系的数据元素的集合。 就是说方便在内存中管理数据,进行增删查改的操作。
2.什么是算法?
算法(Algorithm):就是定义良好的计算过程,他取一个或一组的值为输入,并产生出一个或一组值作为输出。简单来说算法就是一系列的计算步骤,用来将输入数据转化成输出结果。
3.数据结构和算法的重要性
目前校园招聘笔试一般采用Online Judge形式, 一般都是20-30道选择题+2道编程题,或者3-4道编程题。


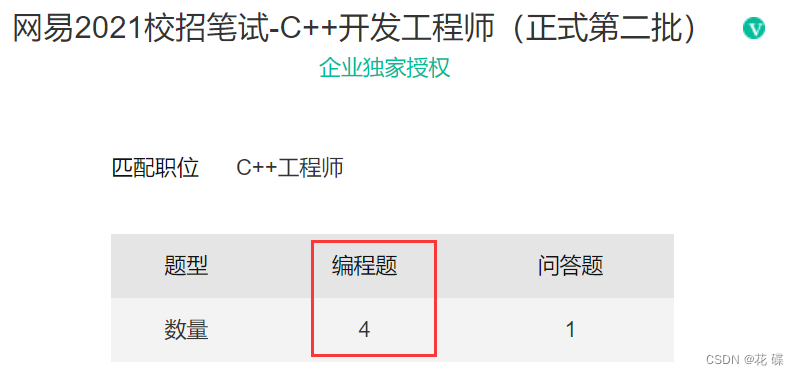
可以看出,现在公司对学生代码能力的要求是越来越高了,大厂笔试中几乎全是算法题而且难度大,中小长的笔试中才会有算法题。算法不仅笔试中考察,面试中面试官基本都会让现场写代码。而算法能力短期内无法快速提高了,至少需要持续半年以上算法训练积累,否则真正校招时笔试会很艰难,因此算法要早早准备。
数据结构与算法对一个程序员来说的重要性? 👈这篇文章是知乎一篇博主对于数据结构与算法的详细介绍,感兴趣的小伙伴们可以看看。
二、算法的时间复杂度和空间复杂度
1.算法效率
如何衡量一个算法的好坏呢?比如对于以下斐波那契数列:
long long Fib(int N) {if(N < 3)return 1;return Fib(N-1) + Fib(N-2); }斐波那契数列的递归实现方式非常简洁,但简洁一定好吗?那该如何衡量其好与坏呢?
2.算法的复杂度
算法在编写成可执行程序后,运行时需要耗费时间资源和空间(内存)资源 。因此衡量一个算法的好坏,一般是从时间和空间两个维度来衡量的,即时间复杂度和空间复杂度。
时间复杂度主要衡量一个算法的运行快慢,而空间复杂度主要衡量一个算法运行所需要的额外空间。在计算机发展的早期,计算机的存储容量很小。所以对空间复杂度很是在乎。但是经过计算机行业的迅速发展,计算机的存储容量已经达到了很高的程度。所以我们如今已经不需要再特别关注一个算法的空间复杂度。
3.复杂度在校招中的考察


4.时间复杂度
👇1.时间复杂度的概念
时间复杂度的定义:在计算机科学中,算法的时间复杂度是一个函数(函数表达式),它定量描述了该算法的运行时间。一个算法执行所耗费的时间,从理论上说,是不能算出来的,只有你把你的程序放在机器上跑起来,才能知道。但是我们需要每个算法都上机测试吗?是可以都上机测试,但是这很麻烦,所以才有了时间复杂度这个分析方式。一个算法所花费的时间与其中语句的执行次数成正比例,算法中的基本操作的执行次数,为算法的时间复杂度。
即:找到某条基本语句与问题规模N之间的数学表达式,就是算出了该算法的时间复杂度。
// 请计算一下Func1中++count语句总共执行了多少次?
void Func1(int N)
{int count = 0;for(int i = 0; i < N ; ++ i){for(int j = 0; j < N ; ++ j){++count;}}for(int k = 0; k < 2 * N ; ++ k){++count;}int M = 10;while(M--){++count;}printf("%d\n", count);
}👻👻计算一下Func1执行的基本操作次数是多少?
👉计算Func1执行的基本操作次数(函数表达式): F(N) = N² + 2 * N + 10
我们接下来给予一些值进行计算F(N)与N的关系
当N = 10 F(N) = 130当N = 100 F(N) = 10210
当N = 1000 F(N) = 1002010
当N = 10000 F(N) = 100020010
结论:我们发现随着N的增大,2*N + 10的结果对F(N)的整体结果影响会越来越小,其主要影响的一项是N²。
所以,实际中我们计算时间复杂度时,我们其实并不一定要计算精确的执行次数,而只需要估算大概执行次数,计算出一个量级就行。那么这里我们使用大O的渐进表示法。
👇2.大O的渐近表示法
👉大O符号(Big O notation):是用于描述函数渐进行为的数学符号。
推导大O阶方法:
1、用常数1取代运行时间中的所有加法常数。
2、在修改后的运行次数函数中,只保留最高阶项。
3、如果最高阶项存在且不是1,则去除与这个项目相乘的常数。得到的结果就是大O阶。
使用大O的渐进表示法以后,Func1的时间复杂度为O(N²)
另外有些算法的时间复杂度存在最好、平均和最坏情况:
🎍最坏情况:任意输入规模的最大运行次数(上界)
🎋平均情况:任意输入规模的期望运行次数
🎄最好情况:任意输入规模的最小运行次数(下界)
👉例如:在一个长度为N数组中搜索一个数据x
最好情况:1次找到
最坏情况:N次找到
平均情况:N/2次找到
在实际中一般情况关注的是算法的最坏运行情况,需要降低预期,考虑最坏的结果。所以数组中搜索数据时间复杂度为O(N)
👇3.常见时间复杂度计算举例
🎀实例1:
// 计算Func2的时间复杂度?
void Func2(int N)
{int count = 0;for(int k = 0; k < 2 * N ; ++ k){++count;}int M = 10;while(M--){++count;}printf("%d\n", count);
}实例1基本操作执行了2N+10次,通过推导大O阶方法知道,时间复杂度为 O(N)
🎀实例2:
// 计算Func3的时间复杂度?
void Func3(int N, int M)
{int count = 0;for(int k = 0; k < M; ++ k){++count;}for(int k = 0; k < N ; ++ k){++count;}printf("%d\n", count);
}实例2基本操作执行了M+N次,有两个未知数M和N,无法确定M是否远大于(小于)N,或者说两者接近,所以时间复杂度为 O(M+N)
🎀实例3:
// 计算Func4的时间复杂度?
void Func4(int N)
{int count = 0;for(int k = 0; k < 100; ++ k){++count;}printf("%d\n", count);
}实例3基本操作执行了100次,通过推导大O阶方法,时间复杂度为 O(1)
注⚠️:O(1)不是1次,指的是常数次。
🎀实例4:
// 计算strchr的时间复杂度?
const char * strchr ( const char * str, int character );实例4 在字符串中寻找字符。好的情况在第1次就找到了,最坏的情况在尾部找到。基本操作执行最好1次,最坏N次,时间复杂度一般看最坏,时间复杂度为 O(N)
🎀实例5:
// 计算BubbleSort的时间复杂度?
void BubbleSort(int* a, int n)
{assert(a);for(size_t end = n; end > 0; --end){int exchange = 0;for(size_t i = 1; i < end; ++i){if(a[i-1] > a[i]){Swap(&a[i-1], &a[i]);exchange = 1;}}if(exchange == 0)break;}
}实例5基本操作执行最好N次,即第一趟进去查找已经是有序的数字了,最好情况是O(N),最坏的情况呢,一共需要N - 1趟嘛,从N - 1 趟开始,执行N - 1次、N - 2、N - 3 …… 3、2 、1,可以看出来,这是一个等差数列求和,最坏执行了N*(N-1)/2次, 通过推导大O阶方法+时间复杂度一般看最坏,故时间复杂度为 O(N^2)
🎀实例6:
// 计算BinarySearch的时间复杂度?
int BinarySearch(int* a, int n, int x)
{assert(a);int begin = 0;int end = n-1;//[begin, end]:begin和end是左闭右闭区间,因此有=号while(begin <= end){int mid = begin + ((end-begin)>>1);if (a[mid] < x)begin = mid+1;else if (a[mid] > x)end = mid-1;elsereturn mid;}return -1;
}实例6 基本操作执行最好1次,最坏O(logN)次,时间复杂度为 O(log₂N)。ps:logN在算法分析中表示是底数为2,对数为N。有些地方会写成lgN
🎀实例7:
// 计算阶乘递归Fac的时间复杂度?
long long Fac(size_t N)
{if(0 == N)return 1;return Fac(N-1)*N;
}实例7 通过计算分析发现基本操作递归了N次,每次调用执行常数次,所以时间复杂度为O(N)
🎀实例8:
// 计算斐波那契递归Fib的时间复杂度?
long long Fib(size_t N)
{if(N < 3)return 1;return Fib(N-1) + Fib(N-2);
}画图分析:
实例8 斐波那契数列每一项都是递归调用两个子项。我们可以将斐波那契数列的调用过程大致用画图画出来,函数往后调用次数会越来越多,但是到最后几次快调用完了的时候,右边的部分会提前加结束,调用次数会大幅度减少,呈现一个三角形(灰色部分为数据缺失部分),画图不够准确,但大体思想可以这么表示。我们发现,其中调用的每一层是2的倍数,可以看作是一个等比数列,运用错位相减的方法,求出基本操作递归了2^(N - 1) - 1次,故时间复杂度为O(2^N)
5.空间复杂度
1.空间复杂度也是一个数学表达式,是对一个算法在运行过程中临时占用存储空间大小的量度
2.空间复杂度不是程序占用了多少bytes的空间,因为这个也没太大意义,所以空间复杂度算的是变量的个数。
3.空间复杂度计算规则基本跟时间复杂度类似,也使用大O渐进表示法。
注意⚠️:函数运行时所需要的栈空间(存储参数、局部变量、一些寄存器信息等)在编译期间已经确定好了,因此空间复杂度主要通过函数在运行时候显示申请的额外空间来确定。
空间复杂度计算举例
🎏实例1:
// 计算BubbleSort的空间复杂度?
void BubbleSort(int* a, int n)
{assert(a);for(size_t end = n; end > 0; --end){int exchange = 0;for(size_t i = 1; i < end; ++i){if(a[i-1] > a[i]){Swap(&a[i-1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}实例1 使用了常数个额外空间,所以空间复杂度为 O(1)
🎏实例2:
// 计算Fibonacci的空间复杂度?
// 返回斐波那契数列的前n项
long long* Fibonacci(size_t n)
{if(n==0)return NULL;long long * fibArray = (long long *)malloc((n+1) * sizeof(long long));fibArray[0] = 0;fibArray[1] = 1;for(int i = 2; i <= n ; ++i){fibArray[i] = fibArray[i - 1] + fibArray [i - 2];}return fibArray;
}实例2动态开辟了N个空间,空间复杂度为 O(N)
🎏实例3:
// 计算阶乘递归Fac的空间复杂度?
long long Fac(size_t N)
{if(N == 0)return 1;return Fac(N-1)*N;
}实例3递归调用了N次,开辟了N个栈帧,每个栈帧使用了常数个空间。空间复杂度为 O(N)
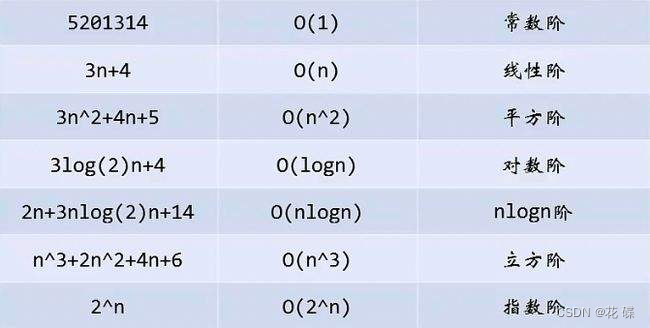
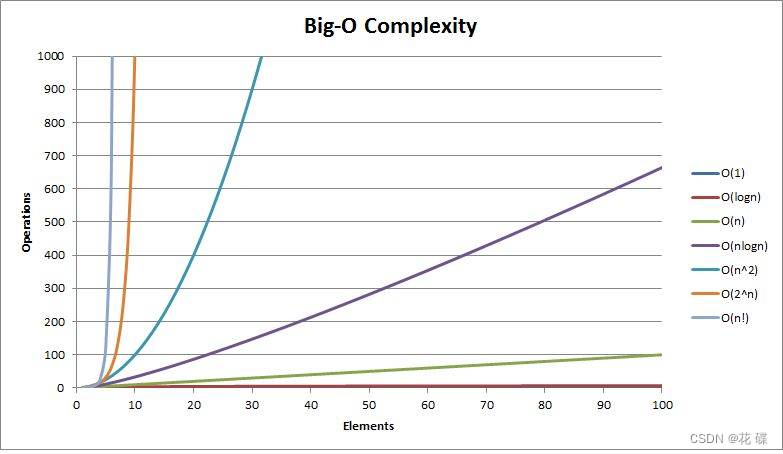
6.常见复杂度对比
一般算法常见的复杂度如下:
7.复杂度的OJ练习
1.消失的数字 17.04 消失的数字_点击链接跳转
2.轮转数组 189.轮转数组_点击链接跳转
🤗🤗 好啦,本篇文章就到此为止啦~ 感谢大家的支持!希望对你有帮助,如有什么疑问,可以在评论区or私信告诉我~~ 🥰🥰😉
相关文章:

【数据结构与算法篇】时间复杂度与空间复杂度
目录 一、数据结构和算法 1.什么是数据结构? 2.什么是算法? 3.数据结构和算法的重要性 二、算法的时间复杂度和空间复杂度 1.算法效率 2.算法的复杂度 3.复杂度在校招中的考察 4.时间复杂度 5.空间复杂度 6.常见复杂度对比 7.复杂度的OJ练…...
HTTP API接口设计规范
1. 所有请求使用POST方法 使用post,相对于get的query string,可以支持复杂类型的请求参数。例如日常项目中碰到get请求参数为数组类型的情况。 便于对请求和响应统一做签名、加密、日志等处理 2. URL规则 URL中只能含有英文,使用英文单词或…...
)
数据一致性校验(pt-table-checksum)
介绍 pt-table-checksum 和 pt-table-sync 是 percona 公司发布的、检查 MySQL 主从数据库数据一致性校验的工具。pt-table-checksum 利用 MySQL 复制原理,在主库执行校验和计算,并对比主从库校验和,由此判断主从库数据是否一致。如果发现数…...

Talk预告 | 新加坡国立大学郑奘巍 AAAI‘23 杰出论文:大批量学习算法加速推荐系统训练
本期为TechBeat人工智能社区第486期线上Talk! 北京时间3月30日(周四)20:00,新加坡国立大学二年级博士生——郑奘巍的Talk将准时在TechBeat人工智能社区开播! 他与大家分享的主题是: “大批量学习算法加速推荐系统训练”,届时将分…...
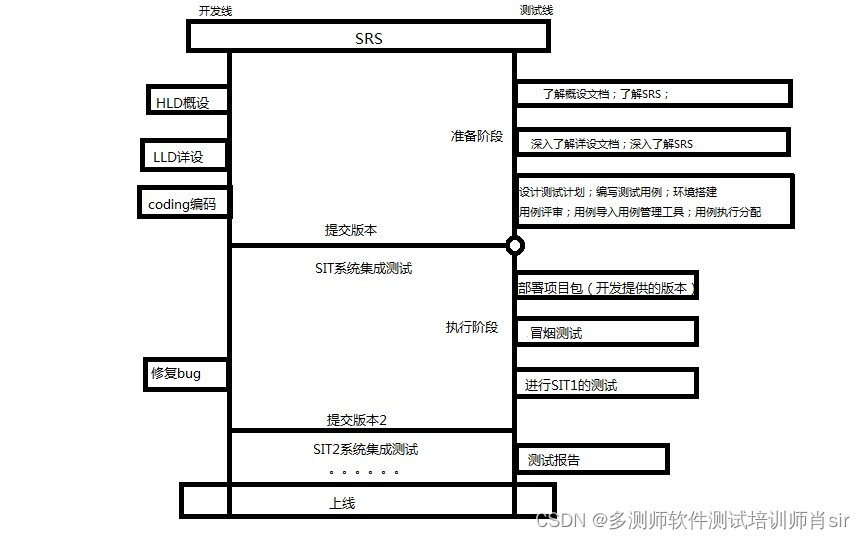
肖 sir_就业课__004项目流程(H模型)
项目流程: 一、面试提问(h模型) 1、你说下你们公司测试流程? 2、给你一个需求你会怎么做? 3、你讲下你的工作? 4、谈谈你是如何去测试? 答案:h模型 要求第一人称来写 讲解简化文字流程&#x…...
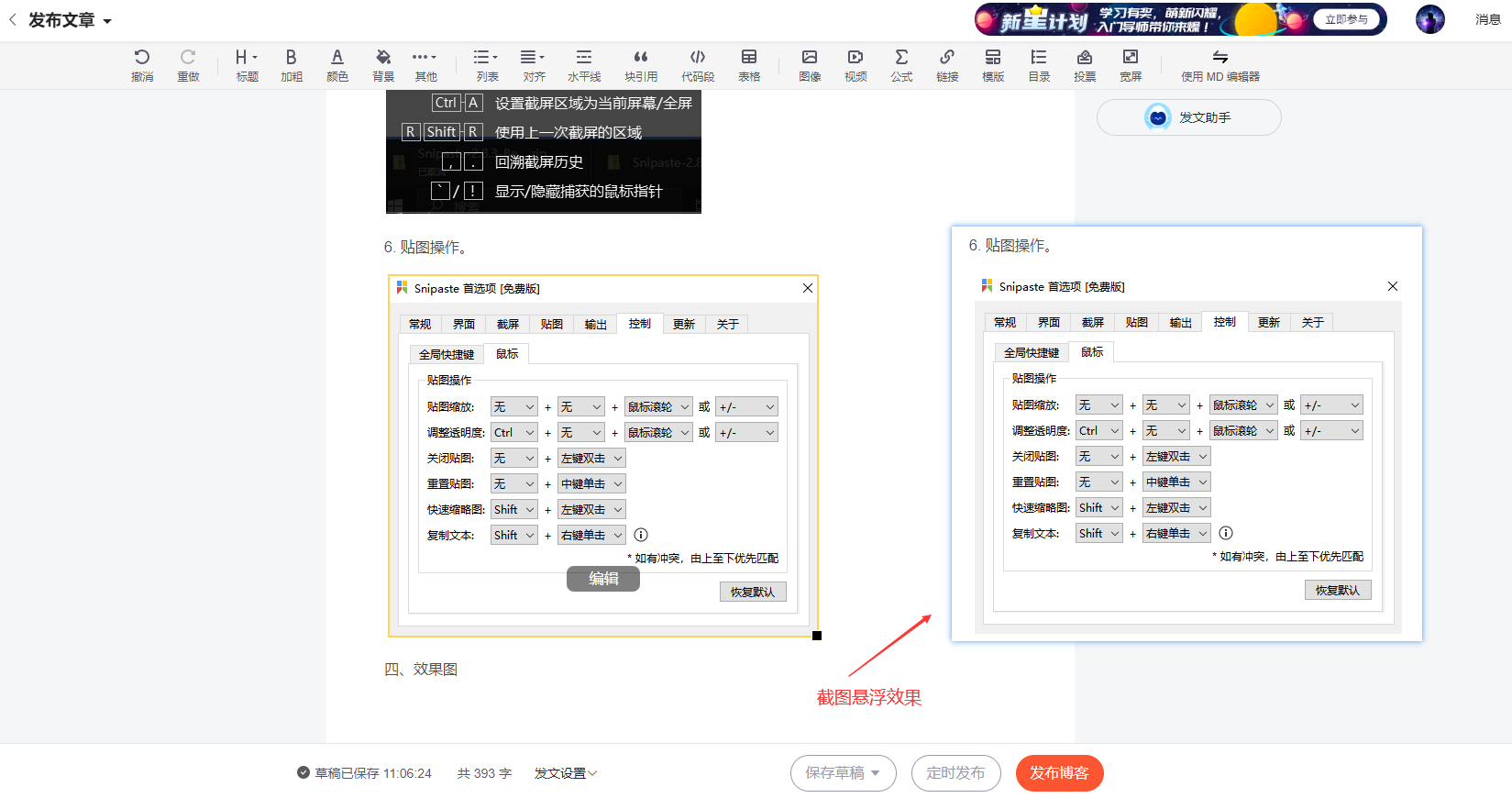
snipaste 截图工具——可以使图片悬浮在任何软件上,方便对比
一、下载 官网下载地址:Snipaste Downloads (需要梯子) CSDN下载地址:https://download.csdn.net/download/weixin_43042683/87671809 1. 下载 压缩包后,免安装,直接解压后既可以使用。 2. 点击Snipaste.…...

Docker 快速部署Springboot项目
编写Dockerfile文件 # Docker image for springboot file run # VERSION 0.0.1 # Author: # 基础镜像使用java FROM openjdk:8 # 作者 MAINTAINER laihx # VOLUME 指定了临时文件目录为/tmp。 # 其效果是在主机 /var/lib/docker 目录下创建了一个临时文件,并链接到…...

【LeetCode: 剑指 Offer II 112. 最长递增路径 | 递归 | DFS | 深度优先遍历 | 记忆化缓存表】
🍎作者简介:硕风和炜,CSDN-Java领域新星创作者🏆,保研|国家奖学金|高中学习JAVA|大学完善JAVA开发技术栈|面试刷题|面经八股文|经验分享|好用的网站工具分享💎💎💎 🍎座右…...
hive 入门 一般用于正式环境 修改元数据(二)
安装配置可参考 https://blog.csdn.net/weixin_43205308/article/details/130020674 1、如果启动过derby,最小初始化过 在安装路径下删除 derby.log metastore_db rm -rf derby.log metastore_db此处省略安装mysql数据库 2、配置MySQL 登录mysql mysql -uroot …...

在RedHat系统上使用firewall-cmd命令可以将端口打开
在RedHat系统上使用firewall-cmd命令可以将端口打开,具体操作如下: 首先,检查当前系统使用的防火墙服务,比如firewalld或iptables,使用以下命令: systemctl status firewalld # 检查firewalld服务 system…...
:免费可用的多种类 API 大全集合整理)
分享(五):免费可用的多种类 API 大全集合整理
前言 搜罗了各大平台整理了一波免费可以用的 API ,有需要的收藏起来啦。 实名认证 运营商二要素 API :运营商校验此姓名、手机号码是否一致。 运营商三要素 API:运营商验证姓名、身份证号码、手机号码是否一致,返回验证结果称…...

8.1 假设验证的基本概念
学习目标: 要学习假设检验的基本概念,我会按照以下步骤进行: 了解假设检验的基本概念:假设检验是一种统计推断方法,用于判断某个假设是否成立。一般来说,假设检验包括原假设和备择假设两个假设,…...

C语言基础
为了学习数据结构,整理一篇基础的C语言入门知识(仅供自身学习用) 条件运算符 语法:exp1 ? exp2 : exp3; exp1是条件表达式,如果结果为真,返回exp2 如果结果为假,返回exp3 if (a > b)max …...

Docker教程:如何将Helix QAC创建为一个容器并运行?
在这个Docker教程中,你将了解到如何将Helix QAC创建为一个容器化的镜像并运行。 Docker的基本定义是一个开源且流行的操作系统级虚拟化(通常称为“容器化”)技术,它是轻量级且可移植的,主要在Linux和Windows上运行。D…...

1676_MIT 6.828 xv6中的CPU alarm_资料翻译整理
全部学习汇总: GreyZhang/g_unix: some basic learning about unix operating system. (github.com) 我觉得看了几个MIT的课程之后让我觉得我的大学四年有点浪费时光,看起来MIT的课程的确是很有饱满度。 这里,再整理一份课程中的作业要求。 …...
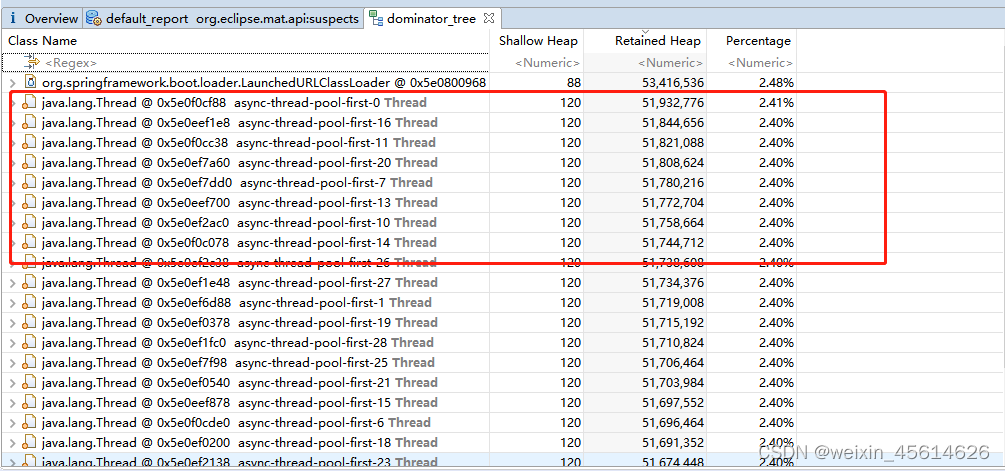
记一次内存泄漏问题的排查
阶段一: 前段时间,突然发现服务在毫无征兆的情况下发生了重启。去看了一下容器退出的日志,发现内存利用率超过了100%,导致容器重启,进一步看了skyWalking,发现heap内存超了,当时只是简单的以为是…...

QML控件--Drawer
文章目录一、控件基本信息二、控件使用三、属性成员一、控件基本信息 Import Statement:import QtQuick.Controls 2.14 Since:Qt 5.7 Inherits:Popup 二、控件使用 Drawer:提供一个可以使用滑动手势打开和关闭的侧面板ÿ…...

PHY- PHY芯片概述
1 PHY概述 关于Internet Protocal的分层模型可以参考文章 :【Internet Protocal-OSI模型中的网络分层模型】,下面我们讲讲底层以太网控制器和收发器的知识。其主要是处理OSI模型中的物理层和链路层的事情。 在CAN/CANFD、FlexRay等总线中,有控制器Controller和收发器Transc…...

【C++】如何获取当前正在运行的函数的名称?
func、FUNCTION、__PRETTY_FUNCTION__的区别 常用获取函数名成的方法都有__func__、FUNCTION、PRETTY_FUNCTION。那么它们的区别是什么呢? 1) func、FUNCTION: 主要是获取函数的名称。 2) PRETTY_FUNCTION: 不仅能获取函数的名称&am…...
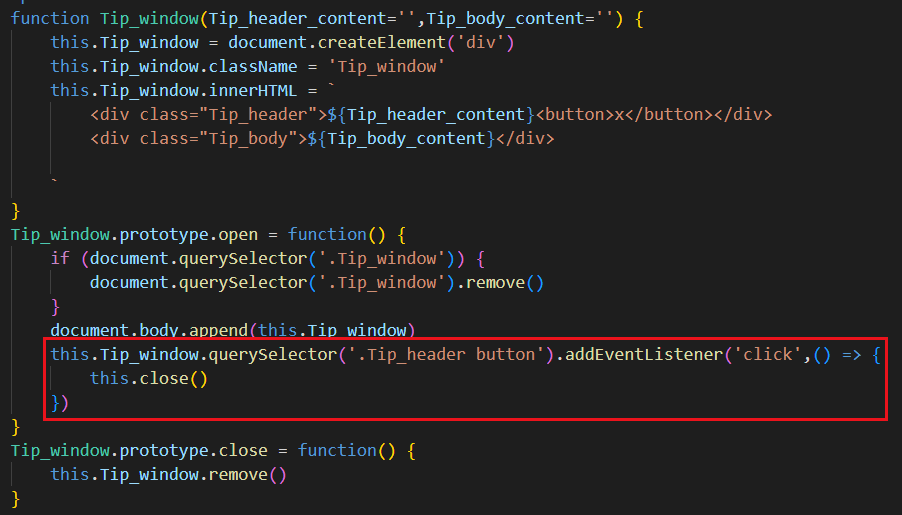
42.原型对象 prototype
目录 1 面向对象与面向过程 2 原型对象 prototype 3 在内置对象中添加方法 4 constructor 属性 5 实例对象原型 __proto__ 6 原型继承 7 原型链与instanceof 7.1 原型链 7.2 instanceof 8 案例-模态框 1 面向对象与面向过程 编程思想有 面向过程 与 面向…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...