8.1 假设验证的基本概念
学习目标:
要学习假设检验的基本概念,我会按照以下步骤进行:
-
了解假设检验的基本概念:假设检验是一种统计推断方法,用于判断某个假设是否成立。一般来说,假设检验包括原假设和备择假设两个假设,通过收集样本数据来进行检验,从而得出结论。
-
熟悉假设检验的步骤:假设检验的一般步骤包括设立原假设和备择假设、选择适当的检验统计量、计算P值和根据P值和显著性水平来做出决策。
-
掌握假设检验中的基本概率分布:在假设检验中,常用的概率分布有正态分布、t分布和卡方分布等。了解这些分布的性质和应用场景,可以帮助我们选择适当的检验方法和计算P值。
-
理解显著性水平的概念:显著性水平是在假设检验中用来判断原假设是否成立的一个重要指标。通常将其设定为0.05或0.01,表示假设检验中允许出现的错误的概率。
-
学习常用的假设检验方法:假设检验方法很多,包括单样本t检验、双样本t检验、方差分析、卡方检验等等。掌握这些方法的应用场景和计算步骤,可以帮助我们在实际问题中应用假设检验方法。
-
实践假设检验:通过实际的数据分析案例,练习假设检验的应用,熟悉假设检验的步骤和方法,进一步掌握假设检验的基本概念。
总之,学习假设检验的基本概念需要掌握一些基本的统计学知识和数学知识,同时需要通过实践来加深理解和熟悉假设检验的应用场景和方法。

概念解释:
假设检验是一种统计推断方法,用于判断一个统计样本的结果是否支持一个关于总体的某个假设。其基本思想是:我们提出一个关于总体的假设(称为原假设),然后收集样本数据,计算出一个样本统计量,并根据该统计量来判断原假设是否应该被拒绝。
假设检验通常包括以下步骤:
-
提出假设:我们要对总体某个参数(比如总体均值、总体比例、总体方差等)提出一个假设,称为原假设(H0),通常包括等式或者不等式。
-
确定检验统计量:从样本中选择一个合适的统计量来表示原假设中所关心的总体参数,通常选择的统计量包括样本均值、样本比例、样本标准差等。
-
设置显著性水平:显著性水平(α)表示我们犯拒绝原假设的错误的风险。通常情况下,显著性水平的常用取值是0.05和0.01。
-
确定拒绝域:拒绝域是指当检验统计量落在一定范围内时,我们将拒绝原假设。拒绝域的界限可以根据样本大小、显著性水平、原假设的具体形式等因素来确定。
-
计算检验统计量:根据样本数据计算出检验统计量的值。
-
做出决策:如果检验统计量的值落在拒绝域内,则拒绝原假设;否则,接受原假设。在做出决策之前,还需要计算p值(p-value),即在原假设为真的情况下,出现检验统计量值或更极端的概率。如果p值小于显著性水平,我们可以拒绝原假设。
假设检验的基本思想是:我们根据样本数据来推断总体的情况,但由于样本数据有一定的随机性,因此在做出判断时需要考虑我们可能会犯的错误。在选择显著性水平和拒绝域时,需要兼顾犯错误的风险和推断的准确性。同时,我们也需要根据样本数据和检验统计量的结果来权衡原假设和备择假设的合理性,以做出恰当的决策。





我的解析:
在统计学中,假设检验是一种判断总体参数(如总体均值、总体比例等)是否与某个特定值相等的方法。在进行假设检验时,我们可能犯两种错误:第一类错误和第二类错误。
第一类错误,也称为α错误,是指在原假设为真的情况下,拒绝原假设的概率。通常,我们会将这个概率控制在一个显著性水平(例如0.05),以确保拒绝原假设的决策不是由于偶然误差所导致。但是,即使原假设为真,仍然有α错误的风险。这种错误通常被认为是“错误地拒绝了真实的原假设”。
第二类错误,也称为β错误,是指在原假设为假的情况下,接受原假设的概率。这种错误通常发生在样本容量太小或样本方差太大时。β错误通常被认为是“未能拒绝错误的原假设”。
总体来说,第一类错误和第二类错误是相互矛盾的。降低一个错误类型的概率会增加另一个错误类型的概率。因此,在进行假设检验时,我们需要根据具体情况选择一个适当的显著性水平和样本容量,以控制这两种错误的风险。
我的理解:
可以这样理解这两类错误:
第一类错误,也就是显著性水平设定的α错误,相当于一个虚假阳性的情况。它表示当原假设为真时,我们错误地拒绝了它,即错误地认为存在一种现象或效应,但事实上不存在。例如,在药物测试中,如果我们错误地得出结论某种药物有效,但实际上它并没有有效,这就是第一类错误。
第二类错误,则是一个虚假阴性的情况。它表示当原假设为假时,我们没有拒绝它,即我们错误地认为不存在一种现象或效应,但实际上存在。例如,在药物测试中,如果我们错误地得出结论某种药物无效,但实际上它是有效的,这就是第二类错误。
在实际应用中,我们需要平衡这两种错误。一般来说,如果第一类错误对于后果非常重要,例如在药物测试中,我们不能容忍一种无效的药物被错误地认为有效,那么我们就需要将显著性水平设置得更小,从而减少第一类错误的风险。但是,这将增加第二类错误的风险,即不能识别出实际上存在的有效现象。因此,我们需要在实际应用中综合考虑这两种错误的风险,选择合适的显著性水平和样本容量。

总结:
假设检验的基本概念包括总体参数、假设、显著性水平、检验统计量、拒绝域等,其中重点和难点、易错点如下:
-
假设:在假设检验中,正确地提出假设是关键。原假设通常表示没有发现任何效应或差异,备择假设则通常表示存在某种效应或差异。但是,有时候提出假设可能会受到数据的影响,因此需要对数据有一定的先验认识。
-
显著性水平:显著性水平是一个关键参数,它决定了我们在多大程度上愿意接受第一类错误(即错误地拒绝原假设)。一般情况下,显著性水平被设定为0.05,但在某些情况下,可能需要根据具体情况进行调整。
-
检验统计量:检验统计量是用于比较样本数据与假设的理论值之间差异的指标。例如,在比较两个总体均值时,常用的检验统计量是t值或z值。在构建检验统计量时,需要考虑总体分布的特征以及样本容量等因素。
-
拒绝域:拒绝域是指所有可能导致拒绝原假设的检验统计量的取值范围。根据显著性水平和假设检验的类型(单侧检验或双侧检验),可以确定拒绝域的范围。在使用拒绝域进行假设检验时,需要注意样本数据是否落在拒绝域内。
-
易错点:假设检验可能会出现的一些易错点包括:(1)未正确提出假设;(2)未正确选择显著性水平;(3)未正确选择检验统计量;(4)未正确计算检验统计量的值;(5)未正确判断样本数据是否落在拒绝域内。为了避免这些错误,需要对假设检验的基本概念有清晰的理解,并严格按照假设检验的步骤进行操作。

相关文章:

8.1 假设验证的基本概念
学习目标: 要学习假设检验的基本概念,我会按照以下步骤进行: 了解假设检验的基本概念:假设检验是一种统计推断方法,用于判断某个假设是否成立。一般来说,假设检验包括原假设和备择假设两个假设,…...

C语言基础
为了学习数据结构,整理一篇基础的C语言入门知识(仅供自身学习用) 条件运算符 语法:exp1 ? exp2 : exp3; exp1是条件表达式,如果结果为真,返回exp2 如果结果为假,返回exp3 if (a > b)max …...

Docker教程:如何将Helix QAC创建为一个容器并运行?
在这个Docker教程中,你将了解到如何将Helix QAC创建为一个容器化的镜像并运行。 Docker的基本定义是一个开源且流行的操作系统级虚拟化(通常称为“容器化”)技术,它是轻量级且可移植的,主要在Linux和Windows上运行。D…...

1676_MIT 6.828 xv6中的CPU alarm_资料翻译整理
全部学习汇总: GreyZhang/g_unix: some basic learning about unix operating system. (github.com) 我觉得看了几个MIT的课程之后让我觉得我的大学四年有点浪费时光,看起来MIT的课程的确是很有饱满度。 这里,再整理一份课程中的作业要求。 …...
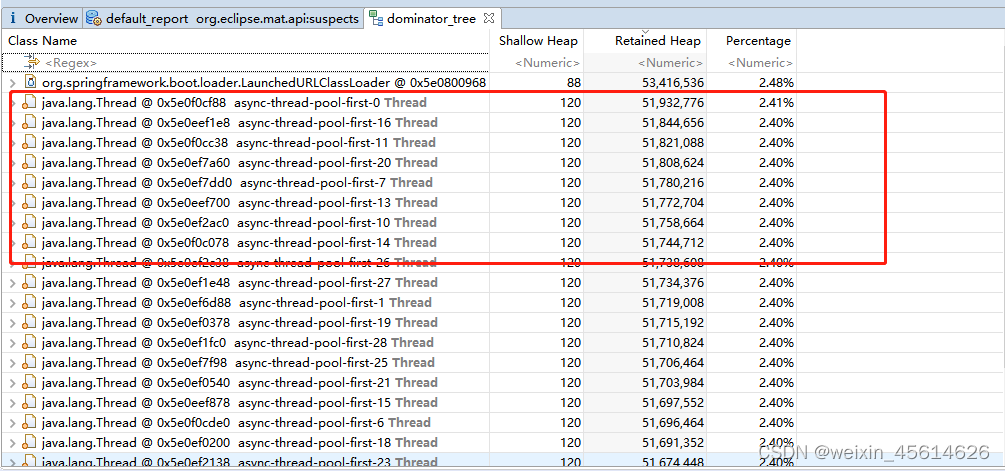
记一次内存泄漏问题的排查
阶段一: 前段时间,突然发现服务在毫无征兆的情况下发生了重启。去看了一下容器退出的日志,发现内存利用率超过了100%,导致容器重启,进一步看了skyWalking,发现heap内存超了,当时只是简单的以为是…...

QML控件--Drawer
文章目录一、控件基本信息二、控件使用三、属性成员一、控件基本信息 Import Statement:import QtQuick.Controls 2.14 Since:Qt 5.7 Inherits:Popup 二、控件使用 Drawer:提供一个可以使用滑动手势打开和关闭的侧面板ÿ…...

PHY- PHY芯片概述
1 PHY概述 关于Internet Protocal的分层模型可以参考文章 :【Internet Protocal-OSI模型中的网络分层模型】,下面我们讲讲底层以太网控制器和收发器的知识。其主要是处理OSI模型中的物理层和链路层的事情。 在CAN/CANFD、FlexRay等总线中,有控制器Controller和收发器Transc…...

【C++】如何获取当前正在运行的函数的名称?
func、FUNCTION、__PRETTY_FUNCTION__的区别 常用获取函数名成的方法都有__func__、FUNCTION、PRETTY_FUNCTION。那么它们的区别是什么呢? 1) func、FUNCTION: 主要是获取函数的名称。 2) PRETTY_FUNCTION: 不仅能获取函数的名称&am…...
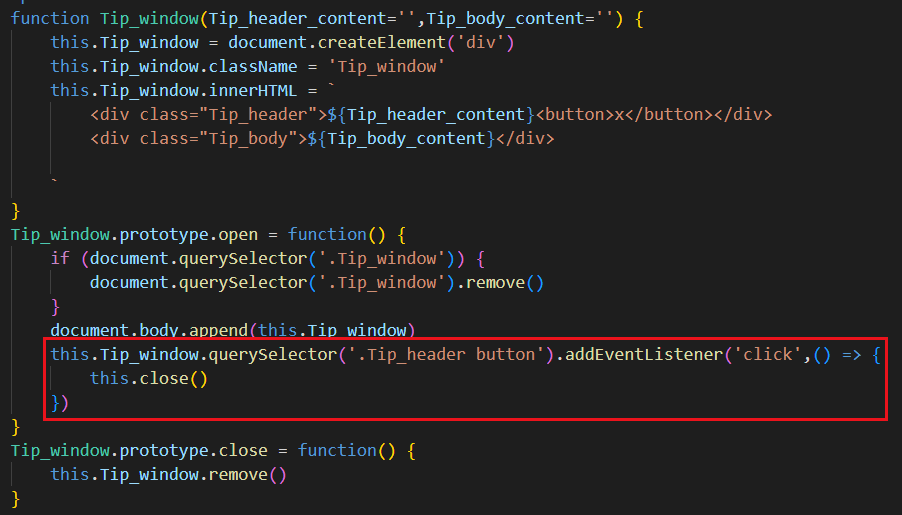
42.原型对象 prototype
目录 1 面向对象与面向过程 2 原型对象 prototype 3 在内置对象中添加方法 4 constructor 属性 5 实例对象原型 __proto__ 6 原型继承 7 原型链与instanceof 7.1 原型链 7.2 instanceof 8 案例-模态框 1 面向对象与面向过程 编程思想有 面向过程 与 面向…...

python 读写txt方法
1. Python支持在程序中读写 txt文件。这里有两种方式: 方式一:使用 python内置函数,该函数将一个字符串的长度转换为与这个字符串长度相关的值。 例如:" readme"("r)。 prin…...
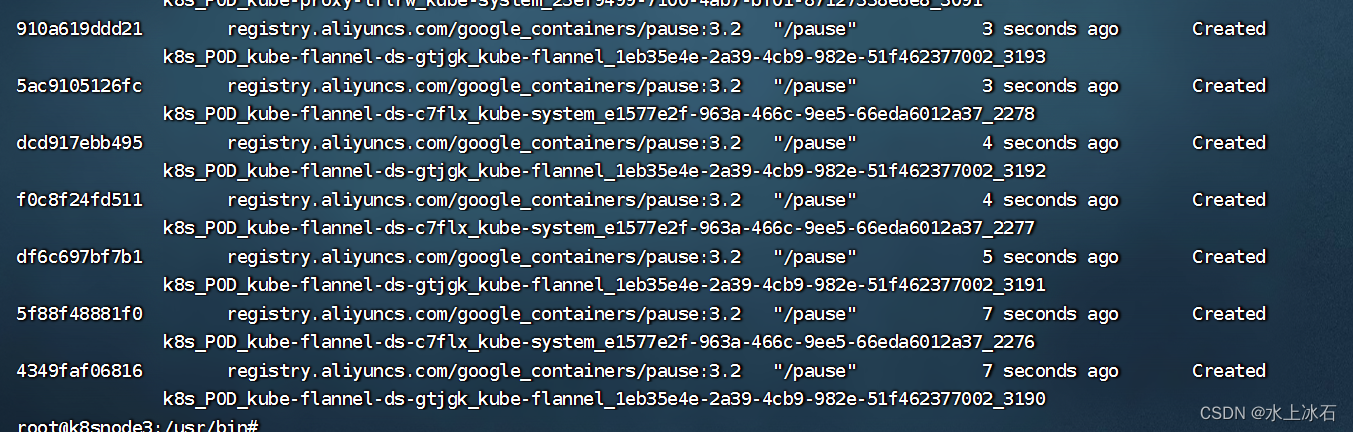
香橙派pi5下,debian,docker19.03.9版本runc容器逃逸
在香橙派pi5下,debian,docker19.03.9版本下,安装系统后,启动docker,显示一切正常。 当加入k8s集群以后,可以正常连接到集群,node状态显示为ready。看起来一切正常。不过过一会之后,香橙派节点内存飙升,然后挂掉。重连失败,需要重启后才能重连。且swapoff -a命令执行…...

Thinkphp6.0中间件.上
本节课我们来学习一下中间件的用法,定义一下中间件。 一.定义中间件 1. 中间件的主要用于拦截和过滤 HTTP 请求,并进行相应处理; 2. 这些请求的功能可以是 URL 重定向、权限验证等等; 3. 为了进一步了解中间件的用法&…...

十进制到八进制的转换
目录 十进制到八进制的转换 程序设计 程序分析 十进制到八进制的转换 【问题描述】对于输入的任意一个非负十进制整数n(0=<n<100000),打印输出与其等值的八进制数 【输入形式】非负十进制整数 【输出形式】相应十进制整数转换后的八进制正整数,若输入不符合要求,…...
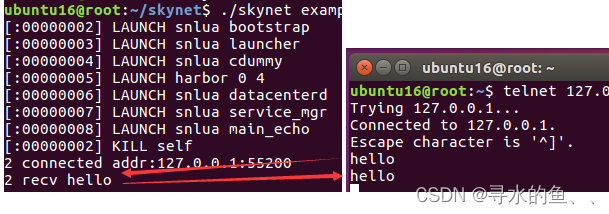
【从零开始学Skynet】基础篇(四):网络模块常用API
游戏服务端要处理客户端请求,作为服务端引擎,网络编程也是Skynet的核心功能。1、学习网络模块 skynet.socket模块提供了网络编程的API,常用的API如下表所示:Lua API说明socket.listen(address ,port)监听一个端口,返回…...

怎么免费制作logo?logo免费设计在线生成,从此设计不求人
你有没有因为Logo制作而烦恼过?对于很多人来说,logo制作是一项比较大的工程,需要专门的设计师才能完成。但是请人设计费用高还很费时间,还需多次沟通修改。其实,我们可以自己免费制作logo,下面,…...

【目标检测】目标检测遇上知识图谱:Object detection meets knowledge graphs论文解读与复现
前言 常规的目标检测往往是根据图像的特征来捕捉出目标信息,那么是否有办法加入一些先验信息来提升目标检测的精准度? 一种可行的思路是在目标检测的输出加入目标之间的关联信息,从而对目标进行干涉。 2017年8月,新加波管理大学…...

IDEA重复下载SNAPSHOT包问题
问题现象 reimport 之后 状态栏显示resolving dependencies… 遇到某个比较大的快照包(33M),同一天的第2个版本时 1.0-xxx-SNAPSHOT.时间戳-2 idea importer 会先分片下载 x.jar.part文件中,然后复制为x.jar吧 如图中所示,其实已经下载完了&…...

【Unity入门】12.MonoBehaviour事件函数
【Unity入门】MonoBehaviour事件函数 大家好,我是Lampard~~ 欢迎来到Unity入门系列博客,所学知识来自B站阿发老师~感谢 (一)常用的事件函数 (1)start和update方法 之前我们写的脚本,会默认帮助…...

1.3 Docker Compose-详细介绍
Docker Compose是一个用于定义和运行多个Docker容器的工具。它可以让用户轻松地定义和管理多个容器的配置,并且可以通过简单的命令来启动、停止和重启这些容器。在本文中,我们将详细介绍Docker Compose的使用和功能。 一、Docker Compose的安装 Docker…...
数据分析:麦当劳食品营养数据探索并可视化
系列文章目录 作者:i阿极 作者简介:Python领域新星作者、多项比赛获奖者:博主个人首页 😊😊😊如果觉得文章不错或能帮助到你学习,可以点赞👍收藏📁评论📒关注…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

并发编程 - go版
1.并发编程基础概念 进程和线程 A. 进程是程序在操作系统中的一次执行过程,系统进行资源分配和调度的一个独立单位。B. 线程是进程的一个执行实体,是CPU调度和分派的基本单位,它是比进程更小的能独立运行的基本单位。C.一个进程可以创建和撤销多个线程;同一个进程中…...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...

系统掌握PyTorch:图解张量、Autograd、DataLoader、nn.Module与实战模型
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文通过代码驱动的方式,系统讲解PyTorch核心概念和实战技巧,涵盖张量操作、自动微分、数据加载、模型构建和训练全流程&#…...

comfyui 工作流中 图生视频 如何增加视频的长度到5秒
comfyUI 工作流怎么可以生成更长的视频。除了硬件显存要求之外还有别的方法吗? 在ComfyUI中实现图生视频并延长到5秒,需要结合多个扩展和技巧。以下是完整解决方案: 核心工作流配置(24fps下5秒120帧) #mermaid-svg-yP…...
实现跳一跳小游戏)
鸿蒙(HarmonyOS5)实现跳一跳小游戏
下面我将介绍如何使用鸿蒙的ArkUI框架,实现一个简单的跳一跳小游戏。 1. 项目结构 src/main/ets/ ├── MainAbility │ ├── pages │ │ ├── Index.ets // 主页面 │ │ └── GamePage.ets // 游戏页面 │ └── model │ …...

数据结构第5章:树和二叉树完全指南(自整理详细图文笔记)
名人说:莫道桑榆晚,为霞尚满天。——刘禹锡(刘梦得,诗豪) 原创笔记:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 上一篇:《数据结构第4章 数组和广义表》…...

